научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 09, сентябрь 2013
DOI: 10.7463/0913.0618917
УДК 01.04.01
Россия, МГТУ им. Н.Э. Баумана
Частотные характеристики широко применяются в анализе систем автоматического управления для исследования систем и ее элементов по экспериментальным данным.
Оценка качества работы таких систем определяется в конечном итоге при экспериментальной отработке реальных образцов. При этом может возникнуть задача идентификации системы и отдельных ее звеньев. В данной статье рассматривается метод идентификации динамических звеньев по их реакции на гармонический сигнал.
Частотная передаточная функция линейного динамического звена с постоянными параметрами описывается в частотной области соотношением [1]
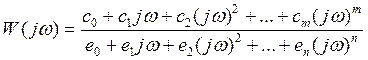 . (1)
. (1)
Неизвестные коэффициенты c0, c1,…,cm, e0, e1,…,enчастотной передаточной функции (1) надо определить в результате решения задачи идентификации.
Из соотношения (1) можно получить выражение для частотной передаточной функции [ 1, 2 ]
![]() , (2)
, (2)
где ![]() и
и ![]() - вещественная и мнимая части частотной передаточной функции соответственно.
- вещественная и мнимая части частотной передаточной функции соответственно.
Частотная передаточная функция ![]() может быть изображена на комплексной плоскости в виде годографа [1]. Для этого для каждого значения частоты вычисляются модуль вектора
может быть изображена на комплексной плоскости в виде годографа [1]. Для этого для каждого значения частоты вычисляются модуль вектора ![]() и угол поворота
и угол поворота ![]() вектора. Модуль вектора
вектора. Модуль вектора ![]() есть отношение амплитуды выходного гармонического сигнала к амплитуде входного гармонического сигнала, а угол поворота
есть отношение амплитуды выходного гармонического сигнала к амплитуде входного гармонического сигнала, а угол поворота ![]() вектора представляет собой сдвиг фаз между выходным гармоническим сигналом и входным гармоническим сигналом. На рис. 1 представлен вид годографа, построенного по соотношению (2) для звена второго порядка (
вектора представляет собой сдвиг фаз между выходным гармоническим сигналом и входным гармоническим сигналом. На рис. 1 представлен вид годографа, построенного по соотношению (2) для звена второго порядка (![]() ).
).
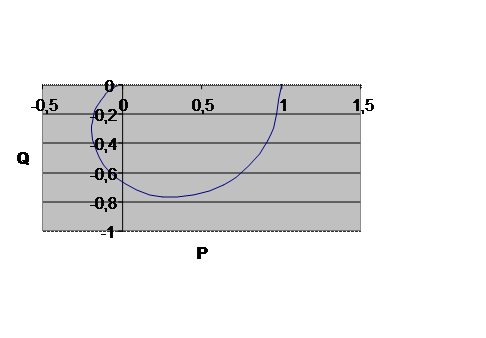
Рис. 1. Годограф динамического звена второго порядка
Амплитуд ![]() и фаза
и фаза ![]() частотной передаточной функции определяются из соотношений
частотной передаточной функции определяются из соотношений
![]() ,
, 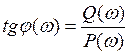 .
.
При получении частотных характеристик реальных звеньев в эксперимент вмешиваются помехи, в результате которых точки годографа смещаются случайным образом. Введем обозначения для определенных с погрешностями вещественных и мнимых значений отсчетов экспериментально полученного годографа ![]() динамического звена для nexp значений частот
динамического звена для nexp значений частот ![]() :
:
![]() . (3)
. (3)
На рис. 2 показан пример искажения экспериментально полученного годографа динамического звена второго порядка относительно годографа, приведенного на рисунке 1 при наличии случайных погрешностей в экспериментальных данных ![]() для nexp=12.
для nexp=12.
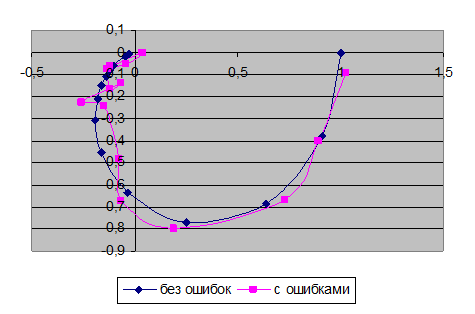
Рис. 2. Пример искажения экспериментально полученного годографа динамического звена второго порядка при наличии случайных погрешностей в экспериментальных данных
Решение задачи идентификации будем искать в классе годографов, задаваемых моделью
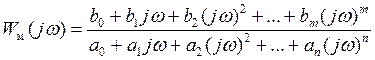 , (4)
, (4)
или в виде
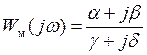 , (5)
, (5)
где
![]() ,
,
![]() ,
,
(6)
![]() ,
,
![]() .
.
Отклонение ![]() i-ого отсчета
i-ого отсчета ![]() годографа модели на частоте
годографа модели на частоте ![]() отопределенного экспериментально i-ого отсчета
отопределенного экспериментально i-ого отсчета ![]() экспериментального годографа идентифицируемого звена
экспериментального годографа идентифицируемого звена
![]()
с учетом (3) и (5)можно записать в виде
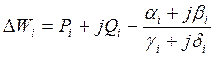 , (7)
, (7)
где параметры ![]() соответствуют частоте
соответствуют частоте ![]() .
.
Необходимо ввести приемлемый критерий, характеризующий близость двух годографов на всей совокупности экспериментальных точек, и минимизировать его по параметрам модели звена ![]() . В качестве критерия (меры) близости можно было бы выбрать сумму квадратов модулей расхождений
. В качестве критерия (меры) близости можно было бы выбрать сумму квадратов модулей расхождений ![]() :
:
 . (8)
. (8)
Минимизация меры I приводит к нелинейной системе уравнений для определения коэффициентов ![]() модели. В работе [2], где рассмотрен частный случай идентификации по годографу для получения линейной системы уравнений, применен способ, модификация которого состоит в следующем.Соотношение (8) умножим на отличный от нуля комплексный множитель
модели. В работе [2], где рассмотрен частный случай идентификации по годографу для получения линейной системы уравнений, применен способ, модификация которого состоит в следующем.Соотношение (8) умножим на отличный от нуля комплексный множитель ![]() :
:
![]() . (9)
. (9)
Тогда с учетом (7) для ![]() и для
и для ![]() получим
получим
![]() , (10)
, (10)
![]() .
.
В качестве меры близости J годографов примем сумму квадратов модулей ![]() :
:
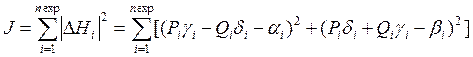 . (11)
. (11)
Следует отметить, что если погрешности определения вещественных и мнимых значений (4) отсчетов экспериментально полученного годографа ![]() равны нулю, то обе меры близости I (8) и J (11) обращаются в нуль.
равны нулю, то обе меры близости I (8) и J (11) обращаются в нуль.
Мера близости Jэкспериментально полученного годографа звена и годографа модели звена на всей совокупности экспериментальных точек задается формулой (11), которая после некоторого преобразования принимает вид
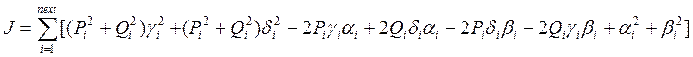 . (12)
. (12)
Мера J (12) является функцией коэффициентов ![]() частотной передаточной функции модели (4). Для минимизации меры J приравняем нулю частные производные от J по этим коэффициентам
частотной передаточной функции модели (4). Для минимизации меры J приравняем нулю частные производные от J по этим коэффициентам
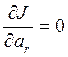 , r=1, ,n ,
, r=1, ,n , 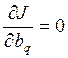 , q=1, ,m. (13)
, q=1, ,m. (13)
В выражениях (6) параметры ![]() зависят только от четных или нечетных коэффициентов модели. Поэтому отличные от нуля частные производные, которые потребуются для (13), можно записать в виде
зависят только от четных или нечетных коэффициентов модели. Поэтому отличные от нуля частные производные, которые потребуются для (13), можно записать в виде
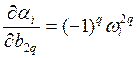 , q=0, 1,…,m/2 ,
, q=0, 1,…,m/2 , 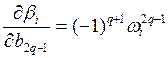 , q=1, 2,…,m/2+1 ,
, q=1, 2,…,m/2+1 ,
(14)
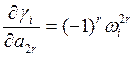 , r=0, 1,…,n/2
, r=0, 1,…,n/2 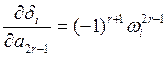 , r=1, 2,…,n/2+1 .
, r=1, 2,…,n/2+1 .
Уравнения (13) с учетом (14) принимают вид
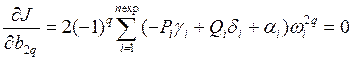 , q=0, 1,…, m/2 ,
, q=0, 1,…, m/2 ,
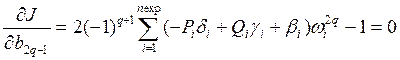 , q=1, 2,…, m/2+1 ,
, q=1, 2,…, m/2+1 ,
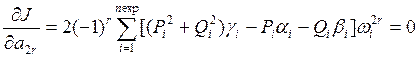 , r=0, 1,…, n/2 ,
, r=0, 1,…, n/2 ,
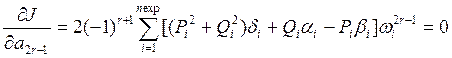 , r=1, 2,…, n/2+1
, r=1, 2,…, n/2+1
или
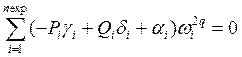 , q=0, 1,…, m/2 ,
, q=0, 1,…, m/2 ,
 , q=1, 2,…, m/2+1 ,
, q=1, 2,…, m/2+1 ,
(15)
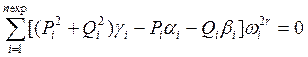 , r=0, 1,…, n/2 ,
, r=0, 1,…, n/2 ,
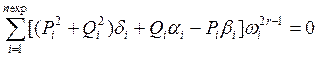 , r=1, 2,…, n/2+1 .
, r=1, 2,…, n/2+1 .
Система уравнений (15) является линейной относительно параметров ![]() , модели (4). Вычисленные из (15) параметры
, модели (4). Вычисленные из (15) параметры ![]() являются коэффициентами частотной передаточной функции модели звена. Они минимизируют выбранную меру J (12) близости годографов и, таким образом, идентифицируют испытуемое динамическое звено, т.е. могут быть использованы в качестве приближенных значений коэффициентов частотной передаточной функции самого звена.
являются коэффициентами частотной передаточной функции модели звена. Они минимизируют выбранную меру J (12) близости годографов и, таким образом, идентифицируют испытуемое динамическое звено, т.е. могут быть использованы в качестве приближенных значений коэффициентов частотной передаточной функции самого звена.
Описание предложенного алгоритма идентификации линейного динамического звена с постоянными параметрами завершим иллюстрацией применения этого алгоритма для линейного звена второго порядка, имеющего передаточную функцию

с коэффициентами ![]() .
.
Проведя nexpэкспериментов, получим экспериментальные значения ![]() (см. (3)).
(см. (3)).
С учетом (8) - (10) частотную передаточную функцию модели звена второго порядка зададим в виде
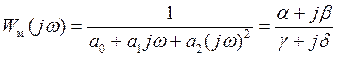 ,
,
где ![]() .
.
Для рассматриваемого звена второго порядка система уравнений (15) принимает вид
![]()
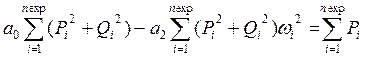 ,
,
![]()
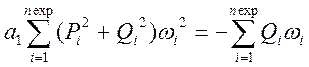 , (16)
, (16)
![]()
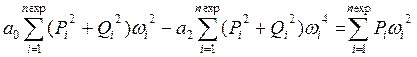 .
.
Систему уравнений (16) приведем к матричному виду
![]() , (17)
, (17)
где
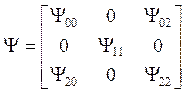 ,
, 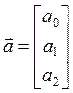 ,
, 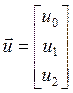 . (18)
. (18)
Ненулевые элементы матрицы ![]() и элементы вектора
и элементы вектора ![]() в (18) имеют значения
в (18) имеют значения
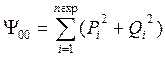 ,
, 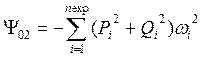 ,
,
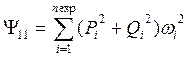 ,
,
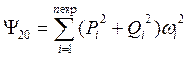 ,
, 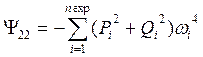 ,
,
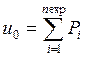 ,
, 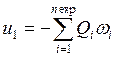 ,
, 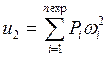 .
.
Решая матричное уравнение (17), получим
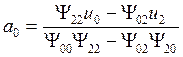 ,
, 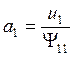 ,
, 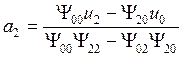 .
.
Были проведены иллюстративные вычислительные эксперименты по оценке погрешности, с которой предложенный алгоритм определяет значения коэффициентов частотной передаточной функции звена второго порядка. В экспериментах заданы конкретные значения коэффициентов ![]() (колебательное звено с собственной частотой 1 1/cи коэффициентом затухания 0,75).
(колебательное звено с собственной частотой 1 1/cи коэффициентом затухания 0,75).
Погрешности измерения значений ![]() моделировались с помощью датчика случайных чисел с равномерным законом плотности распределения вероятностей в различных диапазонах [-0,01, 0,01], [-0,05, 0,05], [-0,1, 0,1]. Количество отсчетов в годографе звена (т.е. количество экспериментов) nexp =6, 12, 24, 48. Для каждого конкретного количества экспериментов nexp проводилось nseriyсерий этих экспериментов nseriy=25.50, 100, 200, 400.
моделировались с помощью датчика случайных чисел с равномерным законом плотности распределения вероятностей в различных диапазонах [-0,01, 0,01], [-0,05, 0,05], [-0,1, 0,1]. Количество отсчетов в годографе звена (т.е. количество экспериментов) nexp =6, 12, 24, 48. Для каждого конкретного количества экспериментов nexp проводилось nseriyсерий этих экспериментов nseriy=25.50, 100, 200, 400.
В сериях экспериментов вычислялись погрешности ![]() ,
, ![]() ,
, ![]() определения коэффициентов
определения коэффициентов ![]() и среднеквадратические отклонения sko для случайных величин
и среднеквадратические отклонения sko для случайных величин ![]() , а также строились гистограммы для этих величин.
, а также строились гистограммы для этих величин.
Для примера на рис. 3 приведены графики зависимости среднеквадратического отклонения sko для погрешности ![]() определения коэффициента
определения коэффициента ![]() от количества отсчетов годографа.
от количества отсчетов годографа.
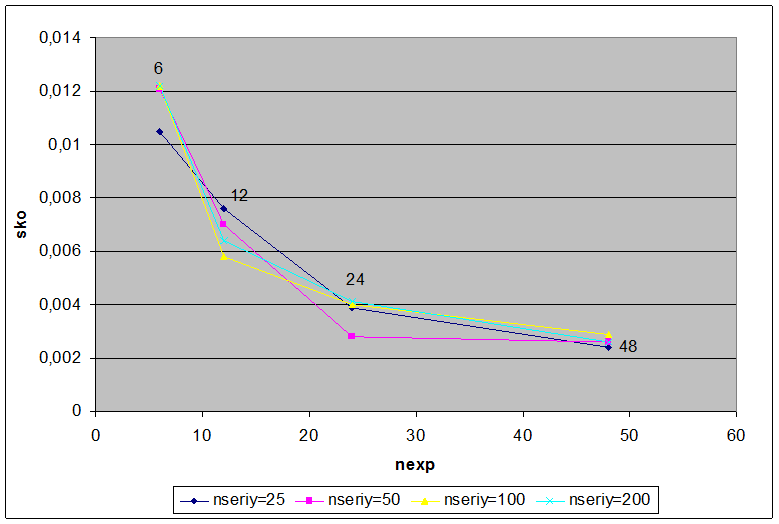
Рис. 3. Зависимость среднеквадратического отклонения sko погрешности ![]() определения коэффициента
определения коэффициента ![]() от количества отсчетов nexpгодографа устройства при погрешности измерений в диапазоне [-0,01, 0,01] и числе серий nseriy=25, 50, 100, 200
от количества отсчетов nexpгодографа устройства при погрешности измерений в диапазоне [-0,01, 0,01] и числе серий nseriy=25, 50, 100, 200
Из рис. 3 видно, что в рассматриваемом случае можно ограничиться количеством отсчетов годографа от 12 до 24. На рис. 4 в качестве примера показана гистограмма погрешности ![]() определения коэффициента
определения коэффициента ![]() .
.
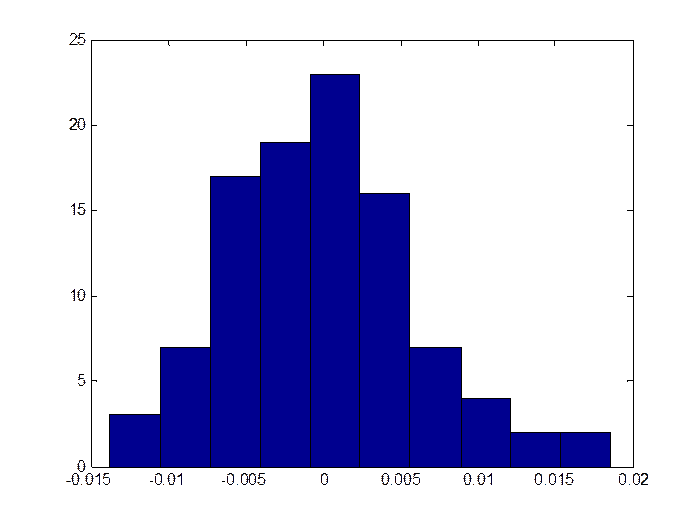
Рис. 4. Гистограмма погрешности ![]() определения коэффициента
определения коэффициента ![]() (nexp=12, диапазон погрешности измерений [-0,01, 0,01], количество серий nseriy=100, среднеквадратическое отклонение sko=0.0058)
(nexp=12, диапазон погрешности измерений [-0,01, 0,01], количество серий nseriy=100, среднеквадратическое отклонение sko=0.0058)
Из рис. 4 видно, что около 95% результатов определения коэффициента частотной передаточной функции модели звена находится в доверительном интервале ![]() 0,0116 относительно фактического значения этого коэффициента
0,0116 относительно фактического значения этого коэффициента ![]() =1. Таким образом, погрешность определения значения коэффициента
=1. Таким образом, погрешность определения значения коэффициента ![]() =1 в иллюстративном вычислительном эксперименте сравнима с диапазоном погрешности измерений отсчетов годографа [-0,01, 0,01].
=1 в иллюстративном вычислительном эксперименте сравнима с диапазоном погрешности измерений отсчетов годографа [-0,01, 0,01].
Аналогичные результаты были получены для погрешностей определения коэффициентов ![]() и
и ![]() . Например, для погрешности
. Например, для погрешности ![]() определения коэффициента
определения коэффициента ![]() (nexp=12, погрешность измерений в диапазоне [-0,01, 0,01], количество серий nseriy=100), среднеквадратическое отклонение sko=0.0072. Для погрешности
(nexp=12, погрешность измерений в диапазоне [-0,01, 0,01], количество серий nseriy=100), среднеквадратическое отклонение sko=0.0072. Для погрешности ![]() определения коэффициента
определения коэффициента ![]() . и (nexp=12, погрешность измерений в диапазоне [-0,01, 0,01], количество серий nseriy=100), среднеквадратическое отклонение sko=0,0097. Для погрешности
. и (nexp=12, погрешность измерений в диапазоне [-0,01, 0,01], количество серий nseriy=100), среднеквадратическое отклонение sko=0,0097. Для погрешности ![]() определения коэффициента
определения коэффициента ![]() (nexp=12, погрешность измерений в диапазоне [-0,05, 0,05], количество серий nseriy=100), среднеквадратическое отклонение sko=0,0122. Для погрешности
(nexp=12, погрешность измерений в диапазоне [-0,05, 0,05], количество серий nseriy=100), среднеквадратическое отклонение sko=0,0122. Для погрешности ![]() определения коэффициента
определения коэффициента ![]() (nexp=12, погрешность измерений в диапазоне [-0,1, 0,1], количество серий nseriy=100), среднеквадратическое отклонение sko=0,0956.
(nexp=12, погрешность измерений в диапазоне [-0,1, 0,1], количество серий nseriy=100), среднеквадратическое отклонение sko=0,0956.
На рис. 5 приведены три годографа: годограф звена, когда погрешность измерения отсчетов годографа равна нулю, годограф звена, когда погрешность измерения отсчетов годографа не равна нулю, годограф найденной модели звена
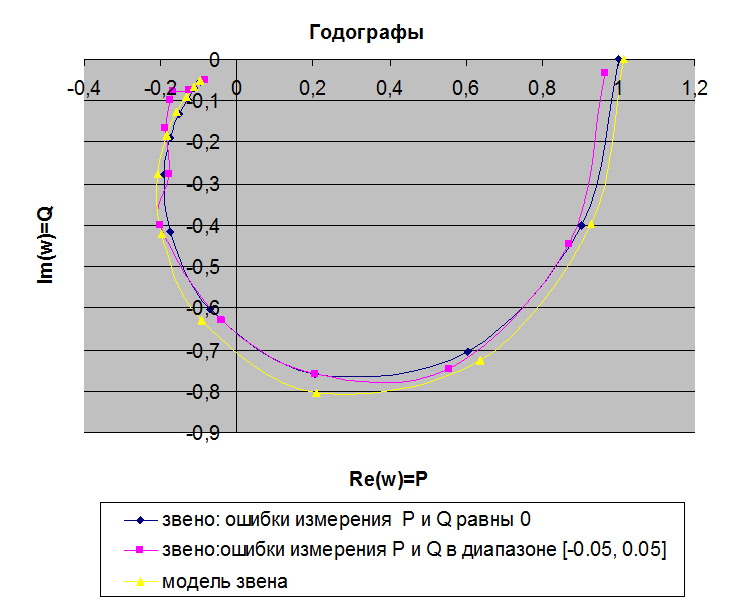
Рис. 5. Годограф звена при нулевой ошибке измерения отсчетов, годограф звена при ненулевых ошибках измерения отсчетов в диапазоне [-0,05, 0,05]; годограф найденной модели звена (количество экспериментов nexp=12
Выводы
В данной статье предложен алгоритм идентификации динамического звена по экспериментально полученным отсчетам частотного годографа звена. В качестве меры близости годографов звена и модели звена выбрана сумма квадратов модулей предложенной авторами модификации отклонений отсчетов годографа модели звена от соответствующих экспериментально полученных отсчетов звена.
В иллюстративном вычислительном эксперименте показано, что для звена второго порядка можно ограничиться количеством отсчетов годографа от 12 до 24.
Иллюстративный вычислительный эксперимент показал, что при использовании предложенного алгоритма идентификации динамического звена по частотному годографу погрешность определения значений коэффициентов частотной передаточной функции звена второго порядка сравнима с диапазоном погрешности измерений экспериментальных отсчетов годографа этого звена.
Список литературы
1. Основы автоматического управления / Под ред. В.С. Пугачева. М.: Наука, 1968. 680 с.
2. Боевкин В.И., Павлов Ю.Н. Регрессионный анализ в прикладной задаче идентификации. М.:Изд-во МГТУ им. Н.Э. Баумана, 1990. (Труды МГТУ им. Н. Э. Баумана; № 546).
Публикации с ключевыми словами: идентификация, линейное динамическое звено, частотный годограф
Публикации со словами: идентификация, линейное динамическое звено, частотный годограф
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



