научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#4 2008
DOI: 10.7463/0408.0087802
УДК 62-5, УДК 531
А. М. Гуськов, Г. Я. Пановко, Чан-Ван-Бинь
Введение. В первой части данной работы [Гус 2008] проведено аналитическое и численное исследование динамики автопараметрического (маятникового) гасителя колебании. Там же обсуждались вопросы эффективности и преимущества маятникового гасителя по сравнению с классическим гасителем колебаний. В настоящее работе рассматриваются результаты экспериментального исследования лабораторной модели (макета) маятникового гасителя колебаний и проводится идентификация параметров расчетной модели. Уточнение математической модели за счет идентификации уровней демпфирования позволяет получить не только качественное, но и количественное совпадение результатов моделирования с наблюдаемыми эффектами.
Схема и общий вид экспериментальной установки приведены на рис. 1.


Рис. 1. Блок-схема (а) и общий вид (б) экспериментальной установки.
Маятник 4, состоящий из стержня длинной l и сосредоточенной массы m, закреплён на одном из концов горизонтальной упругой балке 1. Другой конец балки жестко закреплен на столе электродинамического вибровозбудителя 2 типа ВЭДС-200, совершающего вертикальные гармонические колебания по закону
![]() , (1)
, (1)
где амплитуда ![]() и круговая частота возбуждения
и круговая частота возбуждения ![]()
![]() - техническая частота [Гц]) являются управляемыми параметрами.
- техническая частота [Гц]) являются управляемыми параметрами.
Для управления частотой и амплитудой возбуждения использовался генератор синусоидальных сигналов 6, сигнал от которого через промежуточный усилитель подавался на вибровозбудитель.
Для измерения колебаний использовался виброизмерительный комплекс RFT 5, состоящий из двух пьезоэлектрических акселерометров (датчиков) типа KD-35 и многоканального интегрирующего усилителя типа SM-231.
Один из датчиков устанавливался на столе вибровозбудителя 2 и контролировал уровень возбуждения. Другой датчик устанавливался на балке в точке крепления маятника. Оси чувствительности обоих датчиков ориентировались в вертикальном направлении, что соответствовало направлениям измеряемых колебаний системы. Оба датчика крепились с помощью резьбового соединения. Непосредственно перед измерениями показания датчиков с усилителями калибровались с помощью эталонного датчика.
Физические параметры экспериментальной установки. Значения физических параметров приведены в таблице 1. При выборе длины маятника учитывалось, что автопараметрический гаситель колебаний имеет наилучшие показатели при настройке на внутренний резонанс, который реализуется при собственной частоте малых колебаний маятника в два раза меньшей первой собственной частоты балки (с учетом массы маятника и его крепежа).
Таблица 1.
Параметры | Значения |
L – длина балки [м] | 0,550 |
М0 – масса балки [кг] | 0,851 |
l – длина маятника [м] | 0,023 |
m – масса маятника [кг] | 0,110 |
MМ – суммарная масса крепежа маятника к балке, собственно массы маятника и массы датчика (28 г) [кг] |
0,350 |
Методика проведения эксперимента. В процессе экспериментов задавались дискретные значения частоты возбуждения ![]() в диапазоне от четырех до десяти герц. Шаг частоты возбуждения выбирался в зависимости от близости к резонансу: в непосредственной близости к резонансу он составлял 0,15 Гц (см. табл. 2). Для упрощения последующей обработки экспериментальных результатов на каждой частоте возбуждения задавалась одна и та же амплитуда перемещения стола вибровозбудителя (возбуждения), равная 0,3 мм (контролируемая при этом амплитуда ускорения вычислялась для каждой частоты возбуждения по формуле
в диапазоне от четырех до десяти герц. Шаг частоты возбуждения выбирался в зависимости от близости к резонансу: в непосредственной близости к резонансу он составлял 0,15 Гц (см. табл. 2). Для упрощения последующей обработки экспериментальных результатов на каждой частоте возбуждения задавалась одна и та же амплитуда перемещения стола вибровозбудителя (возбуждения), равная 0,3 мм (контролируемая при этом амплитуда ускорения вычислялась для каждой частоты возбуждения по формуле ![]() ). При этом измерялось значение амплитуды ускорений свободного конца балки (точки крепления маятника)
). При этом измерялось значение амплитуды ускорений свободного конца балки (точки крепления маятника) ![]() .
.
Результаты эксперимента. В таблице 2 приведены результаты измерений для трех серий экспериментов – ![]() .
.
Таблица 2.
╧ | f [Гц] | ае(1) [м/с2] | ае (2) [м/с2] | ае (3)[м/с2] | Ае(1) [мм] | Ае (2) [мм] | Ае (3) [мм] |
1 | 4 | 0,10 | 0,13 | 0,17 | 0,16 | 0,20 | 0,26 |
2 | 4,5 | 0,28 | 0,29 | 0,34 | 0,35 | 0,36 | 0,43 |
3 | 5 | 0,48 | 0,52 | 0,58 | 0,48 | 0,52 | 0,58 |
4 | 5,5 | 0,92 | 0,97 | 1,00 | 0,77 | 0,81 | 0,83 |
5 | 5,75 | 1,40 | 1,40 | 1,45 | 1,07 | 1,07 | 1,11 |
6 | 6 | 2,10 | 2,20 | 2,40 | 1,47 | 1,55 | 1,69 |
7 | 6,25 | 0,80 | 0,80 | 0,83 | 0,52 | 0,52 | 0,54 |
8 | 6,35 | 0,78 | 0,79 | 0,79 | 0,49 | 0,50 | 0,50 |
9 | 6,5 | 0,92 | 0,93 | 0,92 | 0,55 | 0,55 | 0,55 |
10 | 6,55 | 1,25 | 1,20 | 1,18 | 0,74 | 0,71 | 0,69 |
11 | 6,6 | 1,40 | 1,42 | 1,45 | 0,81 | 0,82 | 0,84 |
12 | 6,65 | 1,75 | 1,72 | 1,65 | 1 | 0,98 | 0,94 |
13 | 6,7 | 2,10 | 2,13 | 2,10 | 1,18 | 1,20 | 1,18 |
14 | 6,75 | 2,30 | 2,25 | 2,25 | 1,28 | 1,25 | 1,25 |
15 | 7 | 3,60 | 3,65 | 3,60 | 1,86 | 1,88 | 1,86 |
16 | 7,25 | 4,70 | 4,70 | 4,80 | 2,26 | 2,26 | 2,31 |
17 | 7,5 | 2,30 | 2,27 | 2,30 | 1,03 | 1,02 | 1,03 |
18 | 7,75 | 1,90 | 1,93 | 1,90 | 0,80 | 0,81 | 0,80 |
19 | 8 | 1,55 | 1,60 | 1,55 | 0,61 | 0,63 | 0,61 |
20 | 8,25 | 1,40 | 1,40 | 1,35 | 0,52 | 0,52 | 0,50 |
21 | 8,5 | 1,25 | 1,20 | 1,20 | 0,44 | 0,42 | 0,42 |
22 | 9 | 1 | 1,07 | 1,05 | 0,31 | 0,33 | 0,33 |
23 | 9,5 | 1 | 1 | 1,10 | 0,28 | 0,28 | 0,31 |
24 | 10 | 0,95 | 0,95 | 0,95 | 0,24 | 0,24 | 0,24 |
Амплитуда перемещений ![]() определялась из соотношения
определялась из соотношения ![]() (последние три колонки в таблице 2). Измерения проводились для 24-х значений частоты
(последние три колонки в таблице 2). Измерения проводились для 24-х значений частоты![]() . Таким образом, было проведено 72 эксперимента
. Таким образом, было проведено 72 эксперимента![]() . Частота возбуждения
. Частота возбуждения ![]() (10-ое измерение) соответствует линейному резонансу системы при закрепленном маятнике.
(10-ое измерение) соответствует линейному резонансу системы при закрепленном маятнике.
Следует особо отметить, что в области автопараметрического гашения колебаний балка перемещается как твердое тело (без видимого изгиба). Такое поведение системы представляет определенный интерес и может найти практическое применение, так как при этом существенно снижаются напряжения в конструкции.
Расчетная схема экспериментальной модели. В отличие от рассмотренной в предыдущей работе [Гус 2008] системы с автопараметрическим гасителем колебаний при силовом возбуждении за счет эксцентрикового механизма, данная система имеет кинематическое возбуждение. На рис. 2 показана расчетная схема, соответствующая системе, изображенной на рис. 1.
 |
Рис.2. Расчетная схема экспериментальной установки.
Учитывая, что возбуждение осуществляется вблизи первой собственной частоты системы с закрепленным (неподвижным) маятником, рассматривается механическая система с двумя степенями свободы и влияние массы балки учитывается в виде присоединенной на правом конце массы ![]() , рассчитываемой методом Галеркина. Таким образом, балка считается невесомым упругим элементом длиной
, рассчитываемой методом Галеркина. Таким образом, балка считается невесомым упругим элементом длиной ![]() , с жесткостью на изгиб
, с жесткостью на изгиб ![]() . На правом конце имеется сосредоточенная масса
. На правом конце имеется сосредоточенная масса![]() , с которой связан маятник с невесомым стержнем длиной
, с которой связан маятник с невесомым стержнем длиной ![]() с закрепленной на нижнем конце массой
с закрепленной на нижнем конце массой ![]() . Приведенная масса
. Приведенная масса ![]() вычисляется как
вычисляется как![]() .
.
Уравнения движения автопараметрического маятникового гасителя колебаний при кинематическом возбуждении. При составлении уравнений движения исследуемой модели и последующей идентификации ее параметров по экспериментальным данным необходимо учитывать, что экспериментальная информация о колебаниях системы была получена на основе измерений абсолютных колебаний. Поэтому уравнения движения модели имеет смысл записывать для абсолютных координат. Примем, что абсолютные перемещения концов балки описываются координатой ![]() и
и ![]() , отсчитываемой от статического положения равновесия центра масс балки (сосредоточенной на ее конце)
, отсчитываемой от статического положения равновесия центра масс балки (сосредоточенной на ее конце) ![]() , а колебания маятника – угловой координатой
, а колебания маятника – угловой координатой ![]() , отсчитываемой от вертикали. Приведенная жесткость балки
, отсчитываемой от вертикали. Приведенная жесткость балки ![]() в направлении перемещения
в направлении перемещения ![]() , отсчитываемого вниз от положения равновесия, определяется экспериментально и равна
, отсчитываемого вниз от положения равновесия, определяется экспериментально и равна ![]() .
.
Опуская вывод уравнений движения, который аналогичен выводу системы уравнений (2) в [ГУС 2008], приведем уравнения движения исследуемой системы в виде:
![]() (2)
(2)
Особо подчеркнем, что, несмотря на кинематический характер возбуждения, первое уравнение системы (2) записано для абсолютной координаты ![]() . При этом возмущающее усилие
. При этом возмущающее усилие
![]() (2 а)
(2 а)
где ![]() – коэффициенты демпфирования,
– коэффициенты демпфирования, ![]() - ускорение силы тяжести.
- ускорение силы тяжести.
Учитывая , представим функцию возбуждения ![]() в следующем виде
в следующем виде
![]() (3)
(3)
Для проведения расчетов приведем уравнения к безразмерному виду, используя два масштаба: времени ![]() и линейный
и линейный ![]() :
:
![]() (4)
(4)
Обозначим так же следующие безразмерные комплексы
 (5)
(5)
Тогда уравнения движения примут вид
 (6)
(6)
где
![]() (7)
(7)
Система характеризуется шестью значимыми безразмерными комплексами
![]() (8)
(8)
Для проведения вычислений, система уравнений разрешается относительно вторых производных по времени от обобщенных координат ![]()
 (9)
(9)
где
 (10)
(10)
Идентификация значений параметров модели . Полученные результаты экспериментов использовались для идентификации коэффициентов демпфирования ![]() . Система уравнений численно интегрировалась до установления колебаний при фиксированных значениях параметров
. Система уравнений численно интегрировалась до установления колебаний при фиксированных значениях параметров![]() , назначаемых безразмерных частотах возбуждения
, назначаемых безразмерных частотах возбуждения ![]() в соответствии с таблицей 2. Параметры
в соответствии с таблицей 2. Параметры ![]() выбирались из интервалов
выбирались из интервалов![]() . В установившемся движении определялась расчетная амплитуда колебаний основной массы
. В установившемся движении определялась расчетная амплитуда колебаний основной массы ![]() . Далее вычислялось среднеквадратичное отклонение по всем частотам
. Далее вычислялось среднеквадратичное отклонение по всем частотам
![]() (11)
(11)
В качестве расчетных значений принимаются значения коэффициентов демпфирования, соответствующие минимуму среднеквадратичного отклонения .
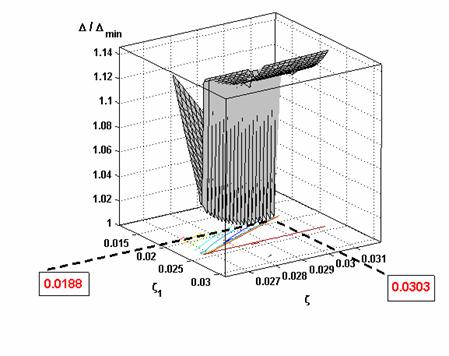
Рис.3. Зависимость целевой функции ![]() от параметров демпфирования
от параметров демпфирования ![]() .
.
На рис. 3 показана поверхность![]() , координаты которой отнесены к минимальному значению
, координаты которой отнесены к минимальному значению ![]() , достигаемому при
, достигаемому при
![]() (12)
(12)
Вычисления проводились на сетке с шагом![]() .
.
На рис. 4 представлены результаты расчетов амплитудно-частотных характеристик, соответствующих экспериментальным данным ![]() и модельным
и модельным ![]() , определенным для оптимальных значений коэффициентов демпфирования . Частоты отнесены к резонансной частоте
, определенным для оптимальных значений коэффициентов демпфирования . Частоты отнесены к резонансной частоте ![]() , амплитуды – к статическому прогибу
, амплитуды – к статическому прогибу ![]() . На рисунке также показана амплитудно-частотная характеристика основной массы при неподвижном маятнике -
. На рисунке также показана амплитудно-частотная характеристика основной массы при неподвижном маятнике - ![]() . Полученные результаты показывают хорошую адекватность расчетной модели.
. Полученные результаты показывают хорошую адекватность расчетной модели.
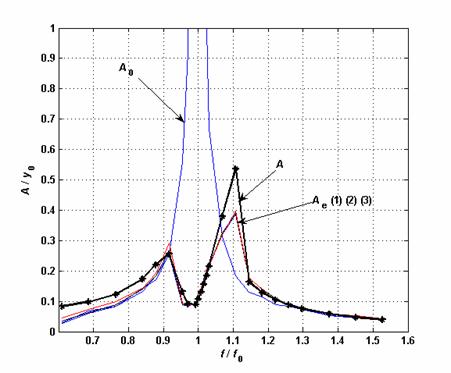
Рис.5. АЧХ основной массы: ![]() - экспериментальные характеристики,
- экспериментальные характеристики,
![]() - теоретическая характеристика,
- теоретическая характеристика, ![]() - теоретическая характеристика, полученная при «выключенном» гасителе колебаний.
- теоретическая характеристика, полученная при «выключенном» гасителе колебаний.
Таким образом, предлагаемая расчетная модель и методика идентификации коэффициентов демпфирования позволяет достаточно точно аппроксимировать поведение автопараметрического гасителя колебаний.
Работа выполнена при поддержке грантов РФФИ 07-08-00253-а, 07-08-00592-а и гранта CRDF НОЦ - 018.
ЛИТЕРАТУРА
[ГУС 2008] Гуськов А.М., Пановко Г.Я., Чан-Ван-Бинь. Дмнамика автопарметрического гасителя колебаний (часть 1) // Наука и образование. Инженерное образование. E-Journal. 2008, ╧2. (http://technomag.edu.ru/doc/80815.html)
Публикации с ключевыми словами: динамическое гашение колебаний, динамика нелинейных систем
Публикации со словами: динамическое гашение колебаний, динамика нелинейных систем
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



