научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 08, август 2011
УДК 652.72
НИИ современных технологий, системного анализа и моделирования, ИрГУПС,
г. Иркутск
Введение. В динамике машин вопросам влияния вибраций на обеспечение надежности и безопасности рабочих процессов и созданию условий для операторов уделяется значительное внимание [1, 2], Известны и достаточно широко применяются различные методы построения математические, в том числе на основе мехатронных интерпретаций [3], что создает предпосылки для обобщенных подходов в задачах поиска и разработки соответствующих способов и средств управления динамическим состоянием механических колебательных систем. В этом плане динамические гасители колебаний, как некоторые дополнительные устройства, вводимые в исходные расчетные схемы виброзащитных систем, могут рассматриваться как одно из средств управления состоянием объекта защиты.
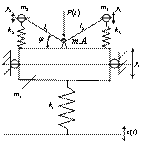
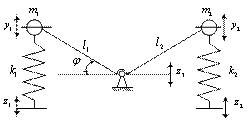
I. Рассмотрим динамический гаситель колебаний в составе виброзащитной системы, обеспечивающей защиту объекта от вибраций со стороны основания и сочленение в m.А [4]. На рис. 1 а, б, где приняты следующие обозначения: P(t) - внешнее силовое возмущение; z(t) - внешнее кинематическое возмущение; m1 - масса объекта защиты; m2 и m3 - массы настраиваемых элементов; k1, k2, k3 - коэффициенты жесткости упругих элементов; φ - угол поворота рычага относительно объекта защиты; l1, l2 - длины плеч рычага; y1, y2, y3 - координаты массоинерционных элементов в абсолютном движении. Предполагается, что колебательные движения в системе относительно положения равновесия достаточно малы, что позволяет использовать упрощенные линейные представления; считается также, что силы трения малы.
II. Постановка задачи. Упрощенный подход. Целью исследования является изучение возможностей создавать в системе режимы динамического гашения, которые могут регулироваться настроечными параметрами, такими как длины плеч рычага и величины масс элементов m2 и m3. Конструктивные варианты построения систем изменения названных параметров представляются вполне реализуемыми, также как и схемы сбора и обработки информации о динамическом состоянии системы. Запишем выражения для кинетической и потенциальной энергий
![]() , (1)
, (1)
![]() . (2)
. (2)
Введем ряд соотношений между координатами ![]() ,
, ![]() , где учтены особенности рычага второго рода в отношении изменения входного сигнала и по величине и по направлению. Будем полагать, что элементы m2 и m3 имеют вертикальное движения, а изгиб рычага в первом приближении, не принимается во внимание (хотя это не так и конфигурация расположения l1 и l2 имеет значение). С учетом связи между координатами y1, y2, y3 и φ выражения (1) и (2) можно записать в виде
, где учтены особенности рычага второго рода в отношении изменения входного сигнала и по величине и по направлению. Будем полагать, что элементы m2 и m3 имеют вертикальное движения, а изгиб рычага в первом приближении, не принимается во внимание (хотя это не так и конфигурация расположения l1 и l2 имеет значение). С учетом связи между координатами y1, y2, y3 и φ выражения (1) и (2) можно записать в виде
![]() , (3)
, (3)
![]() . (4)
. (4)
Используя обобщенное уравнение Лагранжа 2 рода, получим уравнения движения системы
![]() (5)
(5)
![]() (6)
(6)
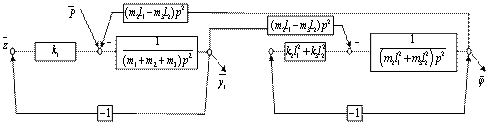
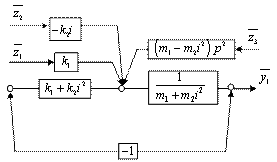
Структурная схема эквивалентной системы автоматического управления (САУ) показана на рис. 1б; из ее анализа следует, что между парциальными системами существует упругая связь, которая при выполнении условий симметрии может «обнуляться» и сделать движения парциальных систем независимыми.
а) | б) |
|
|
Рис. 1. Расчетная (а) и структурная (б) схемы виброзащитной системы с динамическим гасителем и дополнительными связями
| |
Найдем передаточную функцию системы при кинематическом возмущении
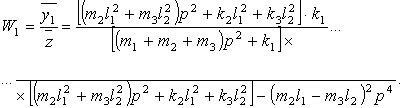 (7)
(7)
Из выражения (7) можно найти частоту динамического гашения при кинематическом возмущении
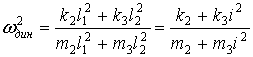 , (8)
, (8)
где i = l2/l1 - передаточное отношение рычага второго рода (знак учтен при составлении выражения для потенциальной энергии). Частота собственных колебаний системы может быть найдена из характеристического уравнения
![]() (9)
(9)
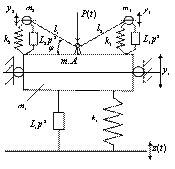
III. Введение дополнительных связей. С целью расширения возможностей изменения динамического состояния в систему можно ввести дополнительные связи в виде элементарных звеньев двойного дифференцирования, как показано на рис. 2 а, б. Расчетная схема (рис. 2а) имеет также устройства с передаточными функциями L1p2 ÷ L3p2 во всех задачах [1].
В этом случае выражения для кинетической энергии примет вид
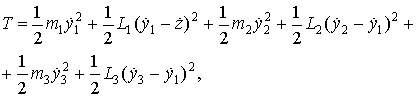 (10)
(10)
а потенциальная энергия определится из выражения (2).
Учитывая соотношения (3) , запишем выражение для кинетической энергии системы
 (11)
(11)
Система дифференциальных уравнений движения примет вид
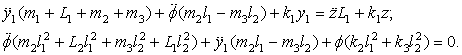 (12)
(12)
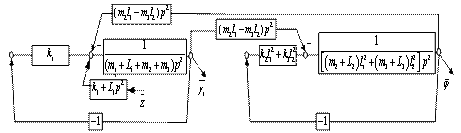
Структурная схема эквивалентной САУ приведена на рис. 2 б.; из структурной схемы следует, что введение устройств с преобразованием движения L1, L2, L3 изменяют свойства системы: L1 влияет на характер внешнего воздействия, а система приобретает дополнительный режим динамического гашения и «запирание» на высоких частотах; введение L2 и L3 – снижают частоты собственных колебаний парциальных систем.
а) | б) |
|
|
Рис. 2. Структурная схема эквивалентной САУ, соответствующей рис. 3
| |
Передаточная функция системы при кинематическом возмущении системы имеет вид:
![]() (13)
(13)
Для исследования преобразуем (13) и получим:
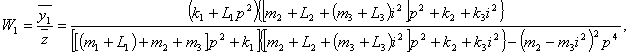 (13')
(13')
где i = l2/l1 – отношение плеч рычага второго рода. Введем ряд обозначений: пусть
![]() ,
,![]() ,
,![]() , тогда
, тогда ![]() – числитель (13) .
– числитель (13) .
Исследуем характеристическое уравнение передаточной функции (13')
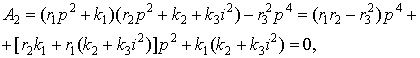
откуда найдем частоты собственных колебаний
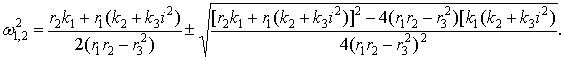 (13'')
(13'')
Если ![]() то разность будет иметь вид
то разность будет иметь вид ![]() , где R – положительный остаток, то есть всегда выполняется ∆ > 0. Если подкоренное выражение (13'') будет равно нулю, то частоты собственных колебаний совпадают и АЧХ системы будут иметь вид, характерный для систем с одной степенью свободы. Из выражения (13') следует, что возможен режим когда
, где R – положительный остаток, то есть всегда выполняется ∆ > 0. Если подкоренное выражение (13'') будет равно нулю, то частоты собственных колебаний совпадают и АЧХ системы будут иметь вид, характерный для систем с одной степенью свободы. Из выражения (13') следует, что возможен режим когда ![]() , что выполняется при
, что выполняется при 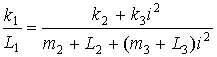 , тогда условие совпадения частот динамического гашения имеет вид:
, тогда условие совпадения частот динамического гашения имеет вид:
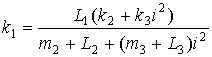 (13''')
(13''')
или 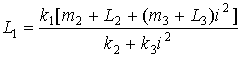 . (14)
. (14)
При выполнении i → ∞ получим предельные соотношения; при этом между значениями параметров должны выполнятся соотношения:
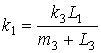 , (15)
, (15)
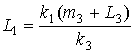 . (16)
. (16)
В свою очередь, при i → 0 получим
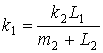 , (17)
, (17)
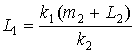 . (18)
. (18)
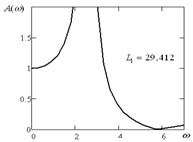
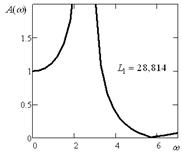
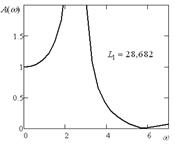
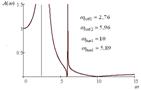
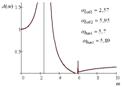
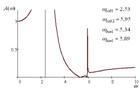
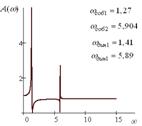
Если выполняется условия (13''') и (14), то система с двумя степенями свободы будет иметь вид АЧХ, как показано на рис. 5, то есть будет ввести себя как система с одной степенью свободы. Расчетным путем могут быть найдены значения L1 (14), соответствующие графикам на рис. 3 при ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
В таблице 1 представлены соответствующие значения частот собственных колебаний и динамического гашения. Для оценки динамических свойств системы передаточная функция, которой представлена выражением (13') при параметрах модельной задачи ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
а) |
б) |
в) |
Рис. 3. Амплитудно-частотные характеристики при условии равенства выражений (13''') и (14) при соответствующих значениях | ||
Таблица 1
Значения частот собственных колебаний и динамического гашения
Значение | Частота собственных колебаний | Частоты динамического гашения |
|
| |
| 2.585 5.855 | 5.831 5.831 |
| 2.586 5.989 | 5.907 5.907 |
| 2.587 5.957 | 5.891 5.891 |
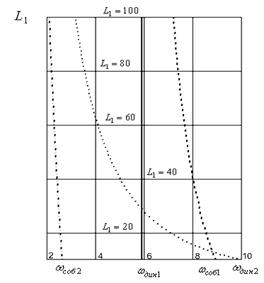
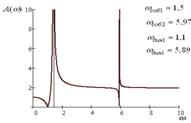
На рис. 4 приведена диаграмма поведения частот динамического гашения и собственных колебаний. В общем случае, учитывая одинаковый порядок частотных уравнений числителя и знаменателя (13'), можно полагать в зависимости от значений параметров, в частности ![]() , что соотношения между частотами, а также формы АЧХ системы, будут
, что соотношения между частотами, а также формы АЧХ системы, будут ![]() изменяться существенным образом.
изменяться существенным образом.
|
Рис. 4. Диаграмма поведения частот динамического гашения и собственных колебаний при изменении параметра
|
На рис. 5 показано, что при изменении ![]() возможны характеристики с двумя режимами динамического гашения и двумя резонансами. Однако, в системе возможны случаи совпадения частот динамического гашения между собой, а также совпадение с частотами собственных колебаний. Для расчетов использовались средства программного пакета Matchad 11. В области высоких частот происходит «запирание» системы. Значение коэффициента передачи амплитуды колебаний при увеличении частоты определяется из выражения (13') при условии, что
возможны характеристики с двумя режимами динамического гашения и двумя резонансами. Однако, в системе возможны случаи совпадения частот динамического гашения между собой, а также совпадение с частотами собственных колебаний. Для расчетов использовались средства программного пакета Matchad 11. В области высоких частот происходит «запирание» системы. Значение коэффициента передачи амплитуды колебаний при увеличении частоты определяется из выражения (13') при условии, что ![]() . Если обозначить эту величину через
. Если обозначить эту величину через ![]() (бесконечность), то значения этого параметра будут зависеть от
(бесконечность), то значения этого параметра будут зависеть от ![]() . На рис. 5 приведена соответствующая информация на вариантах а, б, в, г, д, е, ж. Особенностью амплитудно-частотных характеристик на рис. 5 в ее различных вариантах является то обстоятельство, что система с двумя степенями свободы практически ведет себя как система с одной степенью свободы, что обеспечивается определенными значениями приведенной массо-инерционной характеристики
. На рис. 5 приведена соответствующая информация на вариантах а, б, в, г, д, е, ж. Особенностью амплитудно-частотных характеристик на рис. 5 в ее различных вариантах является то обстоятельство, что система с двумя степенями свободы практически ведет себя как система с одной степенью свободы, что обеспечивается определенными значениями приведенной массо-инерционной характеристики![]() , находимой из выражения (14). Близость резонансных частот создает зону неустойчивых движений повышенного уровня, за пределами которой система имеет вид АЧХ с одной степенью свободы. В качестве изменяемого параметра было, в частности, выбрано передаточное отношение плеч рычажной связи
, находимой из выражения (14). Близость резонансных частот создает зону неустойчивых движений повышенного уровня, за пределами которой система имеет вид АЧХ с одной степенью свободы. В качестве изменяемого параметра было, в частности, выбрано передаточное отношение плеч рычажной связи ![]() . В модельном примере
. В модельном примере ![]() соответствует ,
соответствует , ![]() соответствует
соответствует ![]() ,
, ![]() соответствует
соответствует ![]() (рис. 5). Для АЧХ характерны два участка, на которых коэффициент передачи амплитуды колебаний равен 1 в диапазоне частот
(рис. 5). Для АЧХ характерны два участка, на которых коэффициент передачи амплитуды колебаний равен 1 в диапазоне частот ![]() . В диапазоне частот
. В диапазоне частот ![]() коэффициент передачи амплитуды колебаний меньше единицы, что определяет возможное направление использования системы в задачах виброзащиты.
коэффициент передачи амплитуды колебаний меньше единицы, что определяет возможное направление использования системы в задачах виброзащиты.
IV. Особенности динамических свойств. Характер внешнего воздействия на объект защиты имеет важное значение, поскольку изменяется система динамических связей. Рассмотрим систему, состоящую из двух массоинерционных элементов ![]() и
и![]() , разнесенных с помощью Г-образного рычага с плечами
, разнесенных с помощью Г-образного рычага с плечами ![]() и
и ![]() , как показано на рис. 6. Такая расчетная схема может быть отнесена к одному из двух массоинерционных элементов
, как показано на рис. 6. Такая расчетная схема может быть отнесена к одному из двух массоинерционных элементов ![]() и
и ![]() , разнесенных с помощью Г-образного рычага с плечами
, разнесенных с помощью Г-образного рычага с плечами ![]() и
и ![]() , как показано на рис. 6. Такая расчетная схема может быть отнесена к одному из вариантов вышерассмотренного динамического гасителя при условии, что такой гаситель может либо прикрепляться, либо сниматься с объекта защиты.
, как показано на рис. 6. Такая расчетная схема может быть отнесена к одному из вариантов вышерассмотренного динамического гасителя при условии, что такой гаситель может либо прикрепляться, либо сниматься с объекта защиты.
а) |
б) |
в) |
г) |
д)
| е) |
ж) | |
Рис. 5. АЧХ для выражения (13’) при различных значениях д) при
| |||
| ||||||
Конструктивное использование такого присоединения может быть построено на использовании магнитной подставки. Кинетическая и потенциальная энергия системы (рис. 2) может быть записана в виде
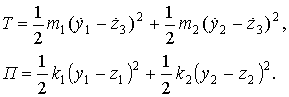 (19)
(19)
Используя соотношение ![]() , где
, где ![]() и представляет собой отношение плеч рычага при малых углах
и представляет собой отношение плеч рычага при малых углах ![]() и без учета наклона стержней, запишем дифференциальное уравнение движения системы
и без учета наклона стержней, запишем дифференциальное уравнение движения системы
![]() (20)
(20)
Структурная схема системы приведена на рис. 6б, откуда может быть найдена частота собственных колебаний
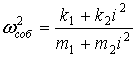 . (21)
. (21)
Из структурной схемы на рис. 6б можно заметить, что внешние воздействия образуют систему, в которой внешние воздействия в силу конструктивных особенностей может действовать в противофазе и создавать нулевое воздействие на любой частоте при ![]() при
при ![]() . Кроме того при
. Кроме того при ![]() для внешнего воздействия
для внешнего воздействия ![]() создается условие «блокирования». Что касается режимов динамического гашения и собственных частот, то необходимо принять во внимание соотношения параметров внешнего кинематического возмущения. Так, например, если
создается условие «блокирования». Что касается режимов динамического гашения и собственных частот, то необходимо принять во внимание соотношения параметров внешнего кинематического возмущения. Так, например, если ![]() , то частота динамического гашения определится по формуле
, то частота динамического гашения определится по формуле
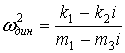 . (21′)
. (21′)
Полагая, что режимы динамического гашения связаны с оценкой числителя передаточной функции, получаемой из структурной схемы на рис. 6б, представим возможные варианты в таблице 2.
Таблица 2
Виды передаточных функций при различных видах внешних возмущениях
╧ п/п | Сочетание параметра внешнего возмущения | Вид передаточной функции | Примечание |
1 | 2 | 3 | 4 |
1 |
|
|
|
2 |
|
| спец. режим |
3 |
|
| спец. режим |
4 |
|
|
|
5 |
|
|
|
6 |
|
| Режима динамического гашения нет |
7 |
|
| Режима динамического гашения нет |
Анализ данных, приведенных в таблице 2, позволяет сделать заключение о том, что режимы динамического гашения встречаются достаточно часто, однако, их появление зависит от особенности конструктивного оформления виброзащитной системы и особенностей системы внешних воздействий.
Заключение. Если в виброзащитную систему (рис.3) ввести дополнительные связи ![]() и
и ![]() , то есть элементарные звенья с передаточными функциям дифференцирования второго рода, то дифференциальное уравнение движения примет вид
, то есть элементарные звенья с передаточными функциям дифференцирования второго рода, то дифференциальное уравнение движения примет вид
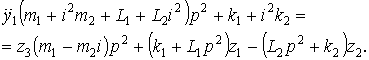 (22)
(22)
Возможный спектр ситуаций, в которых, так или иначе, отражаются свойства режимов динамического гашения, можно оценить, используя уравнение (22). Так, например, при z3 = z1 = z2 = z, получим, что
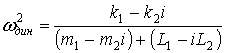 . (23)
. (23)
Отличие выражения (22) от (23) заключается в том, что режим динамического гашения определяется параметрами L1 и L2 устройств для преобразования движения, что расширяет возможности соответствующей настройки виброзащитных систем. Введение сочленений может существенным образом изменять вид амплитудно-частотных характеристик, в том числе обеспечить несколько режимов динамического гашения, включая режимы динамического гашения, выбираемые в дорезонансной области.
Библиографический список
1. Елисеев С.В., Резник Ю.Н., Хоменко А.П., Засядко А.А. Динамический синтез в обобщенных задачах виброзащиты и виброизоляции технических объектов. – Иркутск: Изд-во Ирк. гос. ун-та, 2008. – 523 с.
2. Галиев И.И., Нехаев В.А., Николаев В.А. Методы и средства виброзащиты железнодорожных экипажей. – М.: ГОУ «Учебно-методический центр по образованию на железнодорожном транспорте», 2010. – 340 с.
3. Елисеев С.В., Резник Ю.Н., Хоменко А.П. Мехатронные подходы в динамике упругих колебательных систем. – Новосибирск: Наука. 2010. – 436 с.
4. Елисеев С.В. Возможности сочленения твердых тел в цепных механических системах / С.В. Елисеев, Ю.В. Ермошенко, И.В.Фомина // Современные технологии. Системный анализ. Моделирование – Иркутск: ИрГУПС, ╧3 (27). – 2010. – С. 146 – 152.
Публикации с ключевыми словами: виброзащитная система, динамическое гашение колебаний
Публикации со словами: виброзащитная система, динамическое гашение колебаний
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||