научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 08, август 2011
УДК 621:534; 833
НИИ современных технологий, системного анализа и моделирования,
Иркутский государственный университет путей сообщения, г. Иркутск
Введение. В задачах уменьшения действия вибраций в определенных узлах машин и оборудования часто используются динамические гасители колебаний, представляющие собой дополнительно присоединяемые на упругом подвесе инерционные элементы [1, 2]. В этом направлении последние годы большое внимание уделяется маятниковым гасителям колебаний [3÷5]. Вместе с тем, существуют и другие подходы, в рамках которых могут разрабатываться способы и средства изменения динамического состояния объекта защиты. В частности виброзащитная система, если она имеет несколько степеней свободы, может быть подвержена действию нескольких внешних факторов. Если частоты внешних возмущений совпадают, то одним из путей рационального проектирования виброзащиты могло бы стать управление суммарными силовыми параметрами или групповыми свойствами, что предполагает введение дополнительных внешних сил с целью построения некоторой системы сил, обладающих определенными свойствами [6].
I. Общие положения. Постановка задачи исследования. Рассмотрим виброзащитную систему с двумя степенями свободы (рис. 1), состоящую из объекта массой m1, динамического гасителя m2, упругих элементов k1, k2, k3 и двух внешних сил Q1 и Q2. Предполагается, что внешние гармонические силы могут быть связаны между собой соотношением ![]() , где, в свою очередь,
, где, в свою очередь, ![]() может изменяться в пределах
может изменяться в пределах ![]() , проходя через нулевое значение. Тогда запишем выражение для кинетической и потенциальной энергий системы
, проходя через нулевое значение. Тогда запишем выражение для кинетической и потенциальной энергий системы
![]() ,
, ![]()
и получим систему дифференциальных уравнений, которая может быть записана в виде
![]() (1)
(1)
![]() (2)
(2)
Структурная схема эквивалентной в динамическом отношении системы автоматического управления имеет вид, как показано на рис. 1.
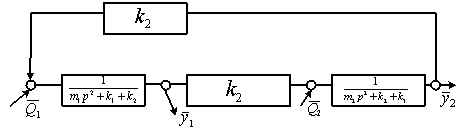
Рис. 1. Структурная схема виброзащитной системы
Запишем формулы для определения координат ![]() и
и ![]() :
:
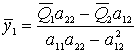 ; (3)
; (3)
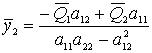 , (4)
, (4)
где ![]() определяются из (1), (2) и представлены в табл. 1.
определяются из (1), (2) и представлены в табл. 1.
Таблица 1
Коэффициенты уравнений движения в системе координат ![]()
|
|
|
|
|
|
|
|
|
|
|
|
Примечание: ![]() и
и ![]() обобщенные силы, приложенные соответственно к элементам системы с массами
обобщенные силы, приложенные соответственно к элементам системы с массами ![]() и
и ![]() .
.
Передаточная функция по координате ![]() в соответствии со схемой на рис. 2 имеет вид:
в соответствии со схемой на рис. 2 имеет вид:
![]() , (5)
, (5)
где ![]() .
.
Режим динамического гашения по координате ![]() можно найти из числителя (3):
можно найти из числителя (3):
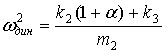 . (6)
. (6)
Найдем критическое значение, при котором ![]() :
:
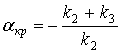 ; (7)
; (7)
то есть при значении ![]() режим динамического гашения не реализуется. Если
режим динамического гашения не реализуется. Если ![]() , то режим динамического гашения возможен: при
, то режим динамического гашения возможен: при ![]() имеем
имеем ![]() ; при
; при ![]() числитель (3) имеет отрицательное значение.
числитель (3) имеет отрицательное значение.
Найдем приведенную жесткость системы по координате ![]() :
:
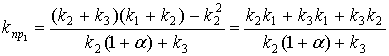 . (8)
. (8)
Если ![]() , то приведенная жесткость
, то приведенная жесткость ![]() будет
будет ![]() . Физически это означает, что точка
. Физически это означает, что точка ![]() при действии силы
при действии силы ![]() не смещается (происходит уравновешивание сил
не смещается (происходит уравновешивание сил ![]() и
и ![]() ), но относительно этого положения возможны колебания. Однако амплитудно-частотная характеристика будет иметь специфичный вид, поскольку передаточная функция (5) изменится
), но относительно этого положения возможны колебания. Однако амплитудно-частотная характеристика будет иметь специфичный вид, поскольку передаточная функция (5) изменится
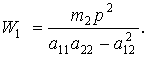 (9)
(9)
Амплитудно-частотная характеристика системы в этом случае начинается с 0, а на высоких частотах – также стремится к 0. Если ![]() будет меньше нуля, то передаточная функция системы примет вид
будет меньше нуля, то передаточная функция системы примет вид
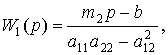 (10)
(10)
где ![]() некоторая величина,
некоторая величина, ![]() . Отрицательный знак приведенной жесткости
. Отрицательный знак приведенной жесткости ![]() не означает потери устойчивости, также как бесконечно большое ее значение при
не означает потери устойчивости, также как бесконечно большое ее значение при ![]() . В данном случае происходит перераспределение направлений движения по координатам, точнее их смещения под действием сил и формирования нового положения равновесия, относительно которого происходит колебания, вызванные периодическими силами
. В данном случае происходит перераспределение направлений движения по координатам, точнее их смещения под действием сил и формирования нового положения равновесия, относительно которого происходит колебания, вызванные периодическими силами ![]() ,
, ![]() .
.
Аналогичным образом может быть рассмотрено и движение по координате ![]() , для которой по формуле Крамера [7]
, для которой по формуле Крамера [7]
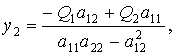 (11)
(11)
откуда передаточная функция системы при входе ![]() и выходе
и выходе ![]() имеет вид
имеет вид
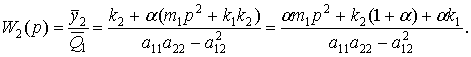 (12)
(12)
Частота динамического гашения по координате ![]() определится
определится
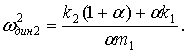 (13)
(13)
Критическое значение ![]() для данного случая составляет
для данного случая составляет
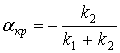 . (14)
. (14)
Приведенная жесткость по координате ![]() имеет вид:
имеет вид:
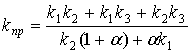 . (15)
. (15)
Из выражения (12) следует, что частоты собственных колебаний системы не зависят от параметра ![]() . Однако, величина частоты динамического гашения колебаний зависит от
. Однако, величина частоты динамического гашения колебаний зависит от ![]() . При
. При ![]() частота динамического гашения будет равна нулю, при изменениях
частота динамического гашения будет равна нулю, при изменениях ![]() в пределах
в пределах ![]() график изменения
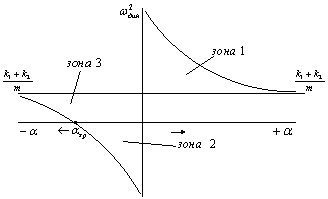
график изменения ![]() показан на рис. 2.
показан на рис. 2.
|
Рис. 2. График зависимости частоты динамического гашения
|
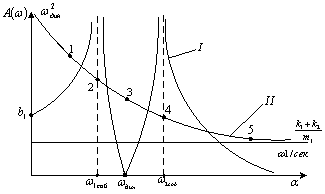
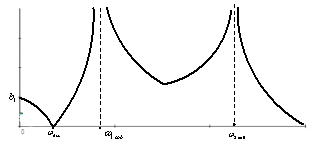
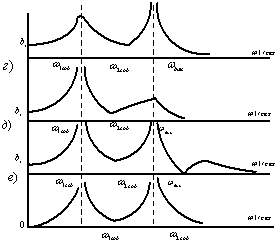
Отметим, что частота динамического гашения изменяется в соответствии со значением ![]() и может находиться в пределах трёх зон: вторая зона соответствует отрицательным значениям квадрата частоты, что не представляет физического интереса; первая и третья зоны дают положительные значения частот, форм амплитудно-частотных характеристик
и может находиться в пределах трёх зон: вторая зона соответствует отрицательным значениям квадрата частоты, что не представляет физического интереса; первая и третья зоны дают положительные значения частот, форм амплитудно-частотных характеристик ![]() , как показано на рис. 3.
, как показано на рис. 3.
а)
|
| |
б)
|
| |
В)
|
| |
Рис. 3. Семейство амплитудно-частотных характеристик системы при различных значениях | ||
При частоте внешних воздействий, соответствующих нулю, начальное значение ![]() , то есть коэффициент передачи амплитуды колебаний будет зависеть от
, то есть коэффициент передачи амплитуды колебаний будет зависеть от ![]() , а само значение
, а само значение ![]() определяется выражением (20).
определяется выражением (20).
Наличие взаимной связи между силами возмущения и управляющей силой, фаза которой может быть настраиваемой, создают эффекты изменения приведенной жесткости системы или приведенной массы. Такой способ настройки системы для защиты объекта соответствует в рамках структурной теории виброзащитных систем [1] способу управления по возмущающей силе. В этом случае настроечный параметр затрагивает только числитель передаточной функции и не влияет на величину частот собственных колебаний.
Таким образом, в системе с двумя степенями свободы при определении частоты динамического гашения и формировании амплитудно-частотных характеристик появляется настроечный параметр ![]() , который может изменяться в достаточно больших пределах.
, который может изменяться в достаточно больших пределах.
Приведенная жесткость при наличии системы внешних сил дает представление о смещении по координате в предположении, что в этой точке приложена обобщенная сила. Такая сила заменяет собой действие исходной системы возмущения, но при такой силе имеется соответствующий коэффициент, который учитывает характер распределения сил. Если ![]() , а податливость в данной точке стремится
, а податливость в данной точке стремится ![]() , то это свидетельствует о формировании положения равновесия, относительно которого могут формироваться колебания объекта рассмотрения. Знак (-) или (+) в значении
, то это свидетельствует о формировании положения равновесия, относительно которого могут формироваться колебания объекта рассмотрения. Знак (-) или (+) в значении ![]() характеризует движение в том или ином направлении от состояния равновесия.
характеризует движение в том или ином направлении от состояния равновесия.
Пусть ![]() если
если ![]() , то
, то
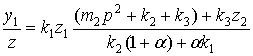 , (16)
, (16)
если ![]()
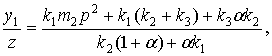 (17)
(17)
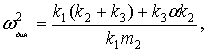 (18)
(18)
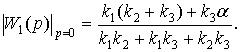 (19)
(19)
С учетом (3), (4) запишем, что
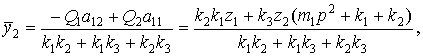 (20)
(20)
тогда:
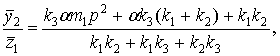 (21)
(21)
откуда 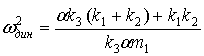 . (22)
. (22)
То есть режимы динамического гашения зависят от системы внешних сил. Режимы эти могут быть или не быть.
Если один из силовых факторов считать внешним возмущением, то второй силовой фактор можно рассматривать как управляемую силу, вводимую для изменения динамического состояния. Контроль за характером изменения состояния можно вести по значению ![]() . Знак и величина
. Знак и величина ![]() определяют вид АЧХ. При
определяют вид АЧХ. При ![]() , что может определяться значением
, что может определяться значением ![]() , АЧХ начинается с нуля.
, АЧХ начинается с нуля.
Если ![]() , то режима динамического гашения по рассматриваемой координате нет.
, то режима динамического гашения по рассматриваемой координате нет.
II. Учет особенностей внешних возмущений. Рассмотрим случай, когда система внешних возмущений имеет силовые и кинематические компоненты.
Пусть ![]() , что вполне допустимо, запишем
, что вполне допустимо, запишем
![]() , а также
, а также ![]()
или
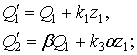 или
или 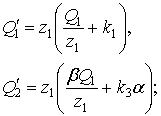 (23)
(23)
то есть систему внешних воздействий ![]() можно привести к одному кинематическому возмущению
можно привести к одному кинематическому возмущению ![]() , но надо ввести параметры
, но надо ввести параметры 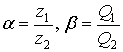 . Нужно еще один параметр – условную пружину, жесткость которой будет равна
. Нужно еще один параметр – условную пружину, жесткость которой будет равна 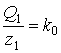 , тогда
, тогда
![]() . (24)
. (24)
Если сила ![]() прикладывается к телу массой
прикладывается к телу массой ![]() и одновременно с этим появляется сила
и одновременно с этим появляется сила ![]() той же частоты и начинает действовать по координате
той же частоты и начинает действовать по координате ![]() , будучи приложена к массе
, будучи приложена к массе ![]() , то можно говорить о групповом эффекте. Сила
, то можно говорить о групповом эффекте. Сила ![]() подчиняет себе или ставит в управление себе силу
подчиняет себе или ставит в управление себе силу ![]() . При этом
. При этом ![]() . В системе происходят изменения. АЧХ изменяется таким образом, как будто бы изменяется жесткость пружины
. В системе происходят изменения. АЧХ изменяется таким образом, как будто бы изменяется жесткость пружины ![]() . Это изменение жесткости определяется параметром
. Это изменение жесткости определяется параметром ![]() , который может иметь отрицательное и положительное значения, проходя через нуль. То есть если
, который может иметь отрицательное и положительное значения, проходя через нуль. То есть если ![]() , то групповое взаимодействие системы внешних сил проявляет себя как введение в систему пружины с соответствующей жесткостью. Вопрос заключается в том, может ли быть такая ситуация реализована. Можно положительно ответить на такой вопрос. Если
, то групповое взаимодействие системы внешних сил проявляет себя как введение в систему пружины с соответствующей жесткостью. Вопрос заключается в том, может ли быть такая ситуация реализована. Можно положительно ответить на такой вопрос. Если ![]() приложено к массе
приложено к массе ![]() как одна из сторон взаимодействия, вызванного помещением электродинамического вибратора между
как одна из сторон взаимодействия, вызванного помещением электродинамического вибратора между ![]() и
и ![]() , то
, то ![]() в соответствии с законами механики (действие равно противодействию). Однако ситуация более универсальная может быть предложена на основе использования двух пар инерционных возбудителей. В принципе, подход может быть распространен и на систему с несколькими степенями свободы. Но суть остается одинаковой – связи между силами эквивалентны по физическому эффекту.
в соответствии с законами механики (действие равно противодействию). Однако ситуация более универсальная может быть предложена на основе использования двух пар инерционных возбудителей. В принципе, подход может быть распространен и на систему с несколькими степенями свободы. Но суть остается одинаковой – связи между силами эквивалентны по физическому эффекту.
Таким образом,
![]() . (25)
. (25)
Если ![]() , то
, то
![]() . (26)
. (26)
Тогда передаточные функции системы определяются
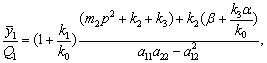 (27)
(27)
![]() (28)
(28)
откуда
![]() , (29)
, (29)
![]() . (30)
. (30)
То есть при возмущении ![]() и установлении связей с остальными силовыми факторами возможны режимы динамического гашения. Отметим, что в выражение для определения частот динамического гашения входят и параметры дополнительно вводимых управляющих сил. В физическом смысле эти силы реализуются как дополнительные упругие элементы, то есть вводимые силы изменяют упругие свойства системы. Подходы, основанные на введении дополнительных сил, управляемых таким образом, чтобы изменять некоторые динамические свойства системы, можно рассматривать как реализацию принципа управления состоянием системы по возмущающему воздействию [7]. Характерным признаком такого управления является возможность изменять только числитель передаточной функции.
и установлении связей с остальными силовыми факторами возможны режимы динамического гашения. Отметим, что в выражение для определения частот динамического гашения входят и параметры дополнительно вводимых управляющих сил. В физическом смысле эти силы реализуются как дополнительные упругие элементы, то есть вводимые силы изменяют упругие свойства системы. Подходы, основанные на введении дополнительных сил, управляемых таким образом, чтобы изменять некоторые динамические свойства системы, можно рассматривать как реализацию принципа управления состоянием системы по возмущающему воздействию [7]. Характерным признаком такого управления является возможность изменять только числитель передаточной функции.
Заключение. Таким образом, при действии на систему нескольких внешних сил при наличии между ними определенных связей, например, по величинам амплитуд возмущений, а также некоторых фазовых соотношениях, система приобретает ряд признаков, которые можно отнести к возможностям реализации принципа управления по возмущению.
Библиографический список
1. Елисеев С.В., Резник Ю.Н., Хоменко А.П., Засядко А.А. Динамический синтез в обобщенных задачах виброзащиты и виброизоляции технических объектов. - Иркутск: Изд-во Ирк. гос. ун-та, 2008. - 523 с.
2. Елисеев С.В., Резник Ю.Н., Хоменко А.П. Мехатронные подходы в динамике механических колебательных систем. - Новосибирск: Наука. 2010. - 430 с.
3. Артюнин, А. И. Применение метода разделения движений для исследования динамики роторной системы с гибким ротором и маятниковым автобалансиром / А. И. Артюнин, Г. Г. Алхунсаев, К. В. Серебренников // Известия вузов. Машиностроение. - 2005. - N 9. - С. 8-14
4. Артюнин, А. И. Об особом режиме движения жесткого ротора с упру гими опорами и маятниковыми автобалансирами / А. И. Артюнин, Г. Г. Алхунсаев // Известия вузов. Машиностроение. - 2005. - N 10. - С. 8-14
5. Елисеев С.В., Волков Л.Н., Кухаренко В.П. Динамика механических систем с дополнительными связями. -Новосибирск: Наука. 1990. - 386 с.
6. Вибрации в технике: справочник в 6 т. Т. 6. Защита оборудования от вибраций / под ред. К.В. Фролова. -М.: Машиностроение. -1983.-586 с.
7. Дружинский И.А. Механические цепи. - Ленинград: Машиностроение.- 1977.-247 с.
Публикации с ключевыми словами: виброзащитная система, динамическое гашение колебаний, управление по возмущению
Публикации со словами: виброзащитная система, динамическое гашение колебаний, управление по возмущению
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||