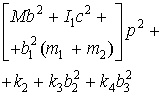научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 03, март 2011
УДК 621.534.833
НИИ современных технологий, системного анализа и моделирования
Иркутский государственный университет путей сообщения
Введение. Вопросы использования динамических гасителей в системах с двумя степенями свободы, при всей изученности проблемы динамического гашения колебаний [1÷3], редко рассматриваются в научной литературе. Вместе с тем, задачи защиты объекта в виде твердого тела на двух упругих опорах имеют значение для инженерной практики, поскольку системы «балочного» типа достаточно широко используются в транспортной динамике [4, 5].
Постановка задачи. Общие положения. Рассмотрим виброзащитную систему, представленную на рис. 1 в виде твердого тела, имеющего массу М и момент инерции I. В точке A находится центр тяжести системы. Его положение определяется соответствующими длинами отрезковl1 и l2. В точке A закрепляется Г-динамический гаситель с массами m1 и m2, разнесенными от шарнирного соединения на расстояния l6 и l7 соответственно. В точках B1 и B2 присоединяются упругие элементы жесткостью k 3 и k4; через l4 иl5 обозначены расстояния точек B1 и B2 от центра тяжести (точки A). Для описания движения выбраны две системы обобщенных координат y1, y2 и y3 (эта система может быть трансформирована в систему координат y1, y2 и φ1, где φ1 - угол поворота Г-образного динамического гасителя колебаний (ДГ) относительно установившегося положения). Вторая система координат определяется координатами y, φ и φ1, где y - координата центра тяжести (или центра масс), φ - угол поворота твердого тела вокруг центра тяжести или центра масс, φ1 -угол поворота динамического гасителя (как вариант этой системы координат, могут быть использованы: y, φ и y3).
|
Рис. 1. Расчетная схема для задач транспортной динамики: AE1=l1,AE2=l2,AB1=l4, AB2=l5, AC=l3; z1 и z2 – кинематические возмущения |
Будем полагать, что на рис. 1 точка A соответствует положению центра тяжести твердого тела без учета динамического гасителя. Если принять, что ДГ устанавливается в точке C, то в такой системе положение центра масс может быть определено по формуле
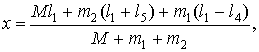 (1)
(1)
где начало координат выбрано в точке E1, совпадающей с концом балки (pис. 1). Если динамический гаситель обладает достаточно большой массой, то центр масс, определяемый по формуле (1), сместится от исходного положения в точке A в другую точку, назовем ее A1. На рис. 2 показано взаимное расположение интересующих нас точек и трансформируем ДГ к плоскому виду.
|
Рис. 2. Расчетная схема системы с упрощенным ДГ и учетом смещения центра масс в т. A1 |
Изменение положения центра масс по сравнению с исходным положением, при котором центр тяжести твердого тела (т. А) и точка прикрепления ДГ (т. С) совпадали бы, характеризуется смещением т. С на величину l3 и определяется по формуле (1). В этом случае расстояние между центром тяжести и центром масс можно найти как
l0=l1 –x. (2)
В дальнейших расчетах будем полагать, что механическая система движется поступательно со скоростью центра масс и вращается при этом вокруг центра масс. Кинетическая и потенциальная энергия системы [6] запишется в виде
![]() (3)
(3)
![]() (4)
(4)
Введем ряд соотношений, необходимых для вывода дифференциальных уравнений движения:
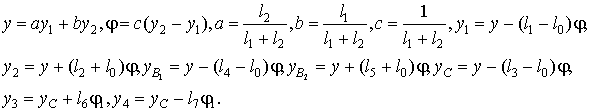
Подробности вывода уравнений движения, соответствующего расчетной схеме на рис. 1, представлена в работе [7]. С учетом (5) можно записать (3) и (4) в виде
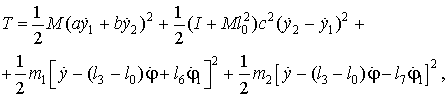 (6)
(6)
 (7)
(7)
Запишем (6), (7) в развернутом виде:
 (8)
(8)
 (9)
(9)
Произведем упрощения (8), (9)
 (10)
(10)
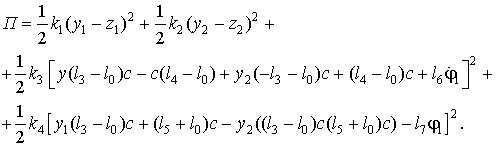 (11)
(11)
Примем ряд соотношений
![]()
![]() (12)
(12)
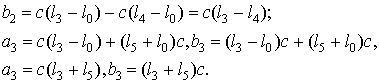
Запишем (10) в виде
 (13)
(13)
В свою очередь:
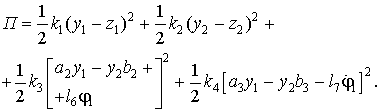 (14)
(14)
Преобразуем (13), (14) к развернутому виду:
 (15)
(15)
 (16)
(16)
Сделаем ряд промежуточных выкладок:
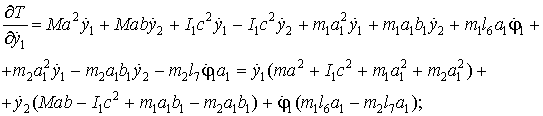 (17)
(17)
 (18)
(18)
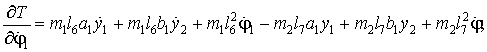 (19)
(19)
 (20)
(20)
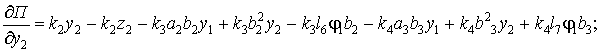 (21)
(21)
 (22)
(22)
Используя (15) ÷ (22), запишем уравнения движения системы в виде:
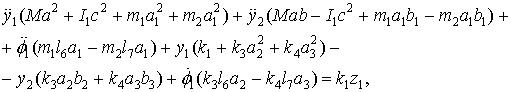 (23)
(23)
 (24)
(24)
 (25)
(25)
Коэффициенты уравнений (23)÷(25) приведены в таблице 1. Для системы в координатах y1, y2 и φ1 характерны перекрестные связи:
· между парциальными системами y1, y2 - инерционно-упругие связи, что предопределяет возможности «зануления» связи;
· между парциальными системами y1 и y3 - инерционно-упругая связь;
· между парциальными системами y2 и y3 - также имеется инерционно-упругая связь.
Найдем частоты «зануления» перекрестных связей, получим:
между y1 и y2 -
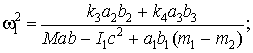 (26)
(26)
между y1 и y3 -
 (27)
(27)
между y2 и y3 -
 (28)
(28)
Передаточные функции системы (при z1 = z2 = z) могут быть найдены из табл. 1 по правилам Крамера [8]:
 (29)
(29)
 (30)
(30)
где
![]() - (30')
- (30')
- характеристическое уравнение.
Решая частотные уравнения числителей (29), (30), найдем, что в системе возможно появление двух частот динамического гашения.
Табл. 1
Таблица коэффициентов системы уравнений (23)÷(25)
в координатах у1, у2, φ1
a11 | a12 | a13 |
|
|
|
a21 | a22 | a23 |
|
|
|
a31 | a32 | a33 |
|
|
|
Q1 | Q2 | Q3 |
k1z1 | k2z2 | 0 |
Примечание:
| ||
Особенности динамических свойств. Рассмотрим работу системы в другой системе координат y, φ и φ1,
![]() (31)
(31)
где ![]()
Преобразуем (31) к детализированному виду:
 (32)
(32)
Сделаем ряд промежуточных выкладок:
 (33)
(33)
 (34)
(34)
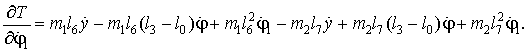 (35)
(35)
Запишем выражение для потенциальной энергии:
![]() (36)
(36)
Примем ряд обозначений:
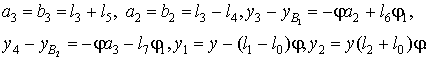
![]() (37)
(37)
Введем соотношения
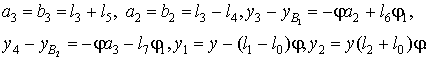
Пусть a4 =l1 - l0, b4 = l2 + l0, тогда выражение (36) преобразуется к виду
 (38)
(38)
или в развернутом виде
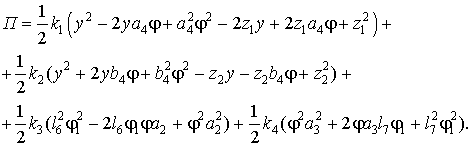 (39)
(39)
Произведем ряд вспомогательных выкладок:
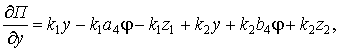 (40)
(40)
 (41)
(41)
 (42)
(42)
Запишем систему уравнений движения:
 (43)
(43)
 (44)
(44)
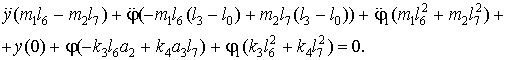 (45)
(45)
Табл. 2
Коэффициенты уравнений движения (43) ÷ (45)
в координатах у, φ и φ1
a11 | a12 | a13 |
|
|
|
a21 | a22 | a23 |
|
|
|
a31 | a32 | a33 |
|
|
|
|
|
|
|
| 0 |
Примечание:
| ||
Коэффициенты уравнений движения в координатах у, φ и φ1 приведены в таблице 2. Отметим, что связи между парциальными системами у, y1 и φ, φ1 носят упруго-инерционный характер и на определенных частотах могут «зануляться», обеспечивая независимость движения:
между парциальными системами y и φ, при этом
 (46)
(46)
между парциальными системами φ и φ1 «зануление» происходит на частоте
 (47)
(47)
Связь между y и φ1 носит инерциальный характер и не «обнуляется».
Передаточные функции для системы координат у, φ и φ1 (при z1 = z2 = z) имеют вид
 (48)
(48)
 (49)
(49)
где A1 определяется выражением (30'). Из частотных уравнений числителей (48), (49) могут быть определены по две частоты динамического гашения. На рис. 3 представлена структурная схема эквивалентной в динамическом отношении системы автоматического управления для расчетной схемы (рис. 2) в координатах у, φ и φ1 . Особенностью структурной схемы является система формирования внешних воздействий, в которой может происходить взаимная компенсация возникающих сил, в частности, при выполнении условий k1a4 = k2b4; в этом случае на парциальную систему φ внешнее возмущение передаваться не будет. Следует отметить, что все динамические взаимодействия в системах рассматриваются в предположении о малости действия сил трения.
Для исследования влияния l0 произведем ряд расчетов. Для оценки динамических свойств решилась модельная задача, в которой были приняты следующие параметры:
M = 100 кг, J = 50 кгм2, m1 = m2 = 5, 10, 20, 50 кг,
K1 = 5000 Н/м, К2 = 7000 Н/м, К3 = 200 Н/м, К4 = 300 Н/м,
l3 = 0 ÷ 0,5 м (с шагом 0,1); l4 = l6 = 0,2; 0,4;
l5 = l7 = 0,2; 0,4; ω = 0 ÷ 15 рад/сек.
На рис. 3 показаны амплитудно – частотные характеристики (АЧХ), построенные с использованием выражений (48). В частотности, можно отметить, что семейство кривых, которые отражают влияние изменения смещения точки установки ДГ на свойства системы (рис. 3б). Для системы характерно наличие двух режимов динамического гашения в до- и межрезонансных частотных областях (рис. 3а). На рис. 3б взаимное расположение АЧХ показано более детализировано.

Влияние изменения l0 характер взаимного расположения АЧХ зависит, существенным образом, от соотношения параметров и выбора координат объекта защиты. На рис. 4 приведено семейство АЧХ по координате y2. Для системы характерным является наличие одного режима колебаний в межрезонансной области. В системе проявляются три режима резонансных колебаний.

Сравнительный анализ АЧХ при различных сочетаниях параметров показывает возможность реализации различных форм кривых, отражающих особенности влияния l0. На рис. 5 приведено семейство АЧХ, отражающее при изменении l0 возможность формирования режима динамического гашения в зарезонансной области (рис. 5а, б).

Особенностью системы является то обстоятельство, что режим резонанса на высшей частоте собственных колебаний не всегда реализуется, поскольку определяемая частота носит комплексно-сопряженный характер. Однако смещение режима динамического гашения за пределы второй частоты собственных колебаний связано формированием некоторого максимума отклонений по координате у2.
Характерная особенность в формировании режимов динамического гашения колебаний приведена на рис. 6 а, б для случая возникновения двух режимов ДГ в межрезонансной области частот; третья частота при данных параметрах не реализуется.
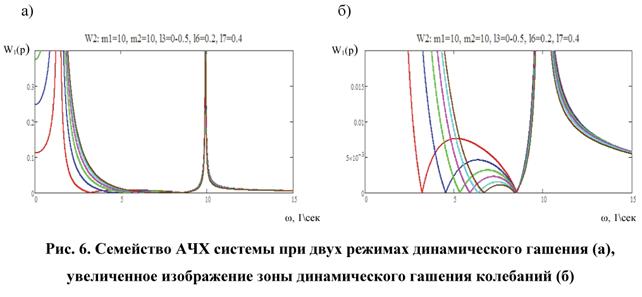
Отметим, что рассмотрение динамических свойств системы с тремя степенями свободы в общем случае предполагает существование трех режимов резонансных явлений, однако при построении АЧХ в силу условий симметрии взаимодействий и комплексности корней характеристического уравнения, вид кривых может носить упрощенный (по числу резонансных пиков) вид; режимы динамического гашения также реализуются в большом разнообразии форм, что отражается в различных вариантах расположения числа режимов динамического гашения колебаний и их места расположения на частотной оси.
Заключение. Предварительная оценка динамических свойств виброзащитных систем с двумя степенями свободы с динамическим гасителем, прикрепляемом через сочленение (или шарнир) показывает возможность изменения достаточно широкого спектра изменения частотных характеристик. В этом плане наибольший интерес для технических приложений представляет возможность вариации точки установки ДГ, а также управления параметрами m1 и m2, l6 и l7, позволяющим изменять не только свойства системы, но ее структуру (например, при выполнении условий m1l6 – m2l7 = 0).
Одним из подходов, которые могли бы иметь продолжение, является оценка возможности реализации совместных режимов динамического гашения по у1 и у2, что соответствует режиму динамического гашения по у, (при этом φ ≠ 0), а также выполнения условий совместного динамического гашения по у и по φ.
Библиографический список
1. Коренев С.В. Динамические гасители колебаний. Теория и технические приложения. / Б.Г. Коренев, П.М. Резников. – М.: Наука., 1963. – 535 с.
2. Елисеев С.В., Нерубенко Г.П. Динамические гасители колебаний. – Новосибирск. : Наука. 1982. – 182 с.
3. Карамышкин В.В. Динамические гасители колебаний. – Л.: Машиностроение. 1988. – 108 с.
4. Ротенберг Р.В. Подвеска автомобиля. / Р.В. Ротенберг – М.: Машиностроение. 1972. – 372 с.
5. Ермошенко Ю.В. Управление вибрационным состоянием в задачах виброзащиты и виброизоляции. // Диссертация на соискание уч. ст. к.т.н. – Иркутск: ИрГУПС. 2002. – 185 с.
6. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики. Том 2. Динамика. – М.: Наука. 1968. – 640 с.
7. Елисеев С.В. Ермошенко Ю.В. Возможные подходы в изменении перекрестных связей в системах с двумя степенями свободы // Системы. Методы. Технологии. Вып. 1(5). Братск.: БрГУ, 2010., с. 20 – 28.
8. Дружинский И.А. Механические цепи – Л.: Машиностроение. / 1977. – 224 с.
Публикации с ключевыми словами: виброзащитная система, динамическое гашение колебаний, сочленение твердых тел
Публикации со словами: виброзащитная система, динамическое гашение колебаний, сочленение твердых тел
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||