научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 09, сентябрь 2013
DOI: 10.7463/0913.0602256
УДК 533.6, 534.83
Россия, МГТУ им. Н.Э. Баумана
Введение
Снижение шума в авиации и на транспорте является актуальной задачей. Основными источниками шума в авиации являются силовая установка и планер с его элементами механизациями (шасси, предкрылки, закрылки, законцовки крыла, каверны), турбулентный пограничный слой на поверхности летательного аппарата. Другим примером источников шума, возникающих в свободном пространстве, являются механизмы турбулентного перемешивания, характерные для пространственных струй [1-3]. Задачи, связанные с моделированием аэродинамического шума ближнего и дальнего поля, получают все большее распространение среди инженеров, занимающихся экспериментом и вычислительной аэрогидродинамикой. На стыке аэродинамики и акустики возникло научное направление – аэроакустика, которая изучает как процессы аэродинамической генерации акустических полей (звука), акустики движущейся среды, взаимодействия звука с потоком, так и методы моделирования вихревых нестационарных турбулентных течений газа и генерируемых ими акустических полей [1].
В вычислительной аэроакустике существует два основных подхода: прямое численное моделирование и гибридные методы. Поскольку во многих случаях требуется вычисление флуктуирующей части давления, определяющей акустическую компоненту, на расстояниях, значительно превышающих характерный размер исследуемого тела, то подход, связанный с прямым численным моделированием шума, является неэффективным. Альтернативой является определение уровня шума интегральными методами, которые представляют собой двухэтапные методы, основанные на раздельном расчёте генерации шума и его распространения. На первом этапе производится гидродинамический расчёт, в процессе которого информация о нестационарных характеристиках потока сохраняется на так называемых контрольных поверхностях. На втором этапе с использованием этой информации производится расчёт распространения звука до положения слушателя с помощью соответствующих интегральных формул или акустических аналогий. В основу гибридных методов положены математические модели на базе URANS/LES/DES подходов, акустические аналогии (Лайтхилла, Керла,Ффоукс– Вильямса – Хоукингса), а также библиотеки, реализующие алгоритмы дискретных преобразований Фурье [3].
В настоящей работе предложена и апробирована методика моделирования турбулентного обтекания тел и расчета акустического давления и спектра шума в ближнем и дальнем поле в трехмерной постановке на основе акустической аналогии и быстрого преобразования Фурье. Данная методика реализована в открытом пакете OpenFOAMв виде разработанной авторами динамической библиотеки libAcoustics.
1. Описание методики моделирования турбулентного обтекания тел и расчета акустического давления и спектра шума в ближнем и дальнем поле.
Анализ исходного кода широко распространенного открытого пакета OpenFOAM показал, что готового решения, которое могло бы использоваться совместно с гидродинамическим расчетом для определения параметров акустического давления и спектра шума не существует. В известных публикациях, где проводились исследования по расчету спектра шума с использованием пакета OpenFOAM, отсутствует какая-либо информация об особенностях программной реализации соответствующих методик. В связи с этим авторами была разработана собственная методика и библиотека libAcoustics, основанная на использовании акустической аналогии Керла и быстрого преобразования Фурье.
Созданная библиотека использует механизм динамических библиотекfunctionObjects API, реализованный в объектно-ориентированном языке программирования C++. Данный механизмявляется интерфейсом, дающим пользователю возможность организации пост-процессинга результатов. Механизм functionObject независим от основного решателя OpenFOAMи может быть использован различными приложениями; он позволяет вызывать нужную библиотеку в требуемой момент расчетного времени и проводить расчеты в параллельном режиме. Динамические библиотеки, использующие этот механизм, активно применяются для выбора физических моделей (модели турбулентности, модель переноса среды и др.).
В основу механизма functionObjectположен принцип наследования языка C++, который позволяет одному объекту приобретать свойства другого объекта; основная идея его использования заключается в следующем:
1) существует прототип класса, который обеспечивает данные для пост-процессинга и содержит виртуальную функцию для пост-процессинга;
2) пользователем создается собственный новый класс, независимый от данного прототипа, который содержит виртуальные функции для пост-процессинга;
3) реализация пользовательского класса располагается в независимой динамической библиотеке.
Список реализации библиотек, использующих механизм functionObject, располагается в специальном массиве (класс с именем functionObjectList); массив таких библиотек располагается в отдельном объекте класса Time. Класс Timeотвечает за исполнение библиотек, основанных на механизме functionObject, в различные моменты расчетного времени. Список всех таких пользовательских библиотек указывается в файле controlDictрасчетного примера OpenFOAM (рис. 1).
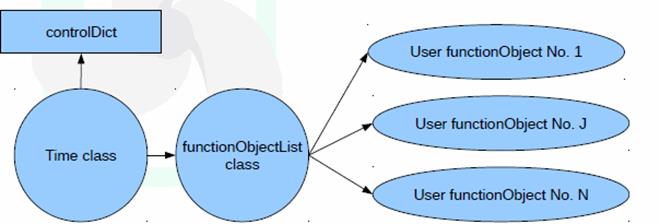
Рис. 1. Схема пользовательских объектов, использующих механизм functionObjects
Разработанная библиотека libAcousticsв OpenFOAM состоит из следующих исходных файлов: Curle.C, CurleFunctionObject.C, CurleFunctionObject.H, Curle.H, SoundObserver.C, SoundObserver.H, FoamFftwDriver.C, FoamFftwDriver.H.
Для работы библиотеки libAcoustics необходимы следующие параметры.
1) Пользовательские данные. Пользователь перед началом расчета должен заранее задать следующие исходные данные: имена граней (патчей), по которым будет проводится интегрирование, имена полей давления и плотности, начальное и конечное время, диапазон частот, для которых проводится исследование, положение слушателя (микрофона), скорость звука, характерную длину, характерное давление, особенности алгоритма быстрого преобразования Фурье для анализа частоты. Чтение исходных данных реализовано с помощью функции Curle.
2) Распределение поверхностной силы, действующую на жидкость со стороны обтекаемого тела. Для определения поверхностной силы нeобходимо проинтегрировать распределение давления по исследуемым поверхностям. Для этого необходимо знать давление в узлах контрольных объемов и координаты векторов нормалей к исследуемым поверхностям.
3) Способ вычисления производной по времени для поверхностной силы. Производная по времени для поверхностной силы может вычисляться с помощью схемы Эйлера или противопоточной схемы.
4) Акустическое давление, уровень звукового давления (SPL) и спектр шума. Акустическое давления определяется для каждого слушателя (микрофона). Для этого введен новый класс SoundObserver. SPLможет быть получен только для преобразования Фурье для акустического давления, т.к. акустическое давление может быть отрицательным. Для работы с разложениями Фурье выполняется простейшая операция: введен новый класс FoamFftwDriver, использующий библиотеку Fftw3. Этот класс в качестве входных данных использует массив значений акустического давления в различные моменты времени в месте расположения слушателя. После выполнения преобразования Фурье возвращается список частот и амплитуд для акустического давления. Далее вычисляется значение SPLпо известной формуле.
5) Порядок сохранения данных на жесткий диск. Организация сохранения данных на жесткий диск осуществляется с использованием класса OFstream, реализованного в составе пакета OpenFOAM. Для каждого слушателя создаются два новых файла: один для акустического давления в различные моменты времени и другой для результатов преобразования Фурье.
6) Параметры вычислений в параллельном режиме. В случае использования параллельных вычислительных алгоритмов необходимо учитывать следующее:
а) исследуемые грани (патчи) могут быть расположены на различных процессорах; для выполнения расчета необходимо «обойти» все процессоры и собрать необходимые данные, это делается с помощью специальных вызовов;
б) преобразование Фурье и операции записи могут быть выполнены на одном процессоре (например, мастере).
Разработанная библиотека позволяет решать широкий класс исследовательских, проектных и эксплуатационных задач, связанных с моделированием вихревых нестационарных турбулентных течений газа и генерируемых ими акустических полей. В результате ее использования возможно численное определение следующих характеристик:
1) акустического давления при обтекании ЛА;
2) спектра шума в ближнем и дальнем поле;
3) диаграммы направленности шума;
4) оценка вклада отдельных элементов конструкции в общий спектр генерируемого шума.
2. Математическая модель.
Предложенная методика включает в себя два основных этапа: расчет параметров течения с использованием соответствующих решателей, входящих в состав пакета OpenFOAM, и акустический расчет на базе разработанной авторами библиотеки libAcoustics.
Гидродинамический расчет производится с помощью одного из входящих в состав пакета OpenFOAMрешателей. В данной работе апробирован решатель pisoFoam, различные численные схемы аппроксимации и интегрирования и различные модели турбулентности.
Математическая модель, положенная в основу решателя pisoFoam, основана на решении осредненных по Рейнольдсу уравнений Навье – Стокса, которые замыкаются с помощью какой-либо модели турбулентности. Обобщенное уравнение, включающее в себя балансовые соотношения для контрольных объемов и модель турбулентности, в наиболее общем виде в интегральной форме можно записать в виде [4]
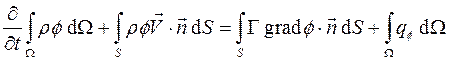 , (1)
, (1)
где ![]() – плотность;
– плотность;![]() – обобщенная переменная,
– обобщенная переменная, ![]() ;
; ![]() – компоненты вектора скорости
– компоненты вектора скорости ![]() вдоль осей Ox, Oy, Oz;
вдоль осей Ox, Oy, Oz; ![]() – турбулентная кинетическая энергия;
– турбулентная кинетическая энергия; ![]() – скорость диссипации турбулентной энергии;
– скорость диссипации турбулентной энергии; ![]() – удельная скорость диссипации турбулентной энергии;
– удельная скорость диссипации турбулентной энергии; ![]() – тензор рейнольдсовых напряжений;
– тензор рейнольдсовых напряжений; ![]() – вектор нормали к поверхности контрольного объема;
– вектор нормали к поверхности контрольного объема; ![]() – коэффициенты переноса;
– коэффициенты переноса; ![]() – источниковый член;
– источниковый член; ![]() – контрольный объем,
– контрольный объем, ![]() – поверхность контрольного объема.
– поверхность контрольного объема.
Для решения полученных систем линейных алгебраических уравнения (СЛАУ) для величин ![]() (
(![]() – турбулентная вязкость) использовался метод бисопряженных градиентов PBiCG (PreconditionedBiconjugateGradient) с предобуславливателем DILU (DiagonalIncompleteLU).
– турбулентная вязкость) использовался метод бисопряженных градиентов PBiCG (PreconditionedBiconjugateGradient) с предобуславливателем DILU (DiagonalIncompleteLU).
Для решения СЛАУ для поправки давления применялся метод PCG (Preconditioned ConjugateGradient) с предобуславливателем DIC (DiagonalIncompleteCholesky).
Для моделирования турбулентности использовались модель ![]() , модель
, модель ![]() Ментера и модель Спаларта-Аллмараса c пристеночными функциями. Модель переноса сдвига напряжений (SST) Ментера включает в себя следующие уравнения [5]:
Ментера и модель Спаларта-Аллмараса c пристеночными функциями. Модель переноса сдвига напряжений (SST) Ментера включает в себя следующие уравнения [5]:
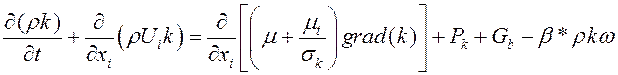
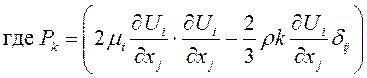
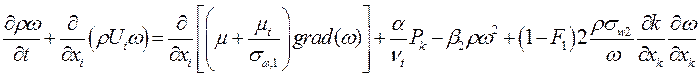
![]()
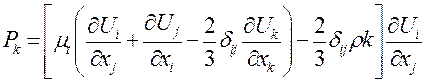
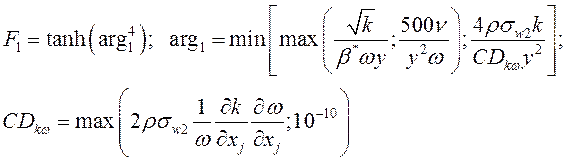
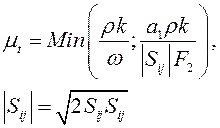 (2)
(2)
Таблица 1. Константы для k-omegaSST модели турбулентности
|
|
|
|
| |
0.09 | 0.083 | 1.0 | 2.0 | 1.17 | 0.44 |
В таблице 1 приведены коэффициенты для выбранной модели турбулентности.
Однопараметрическая модель Спаларта-Аллмараса с одним дифференциальным уравнением для вихревой вязкости. Модель была сконструирована специально для аэрокосмических исследований [5]:
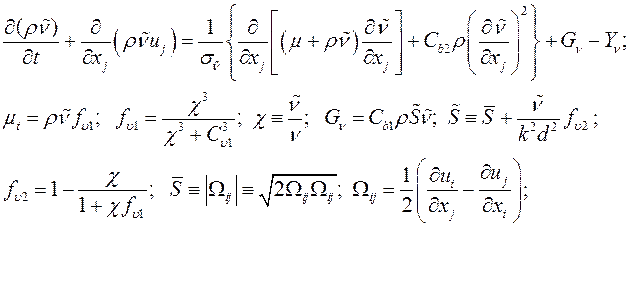 (3)
(3)
скорректированный вариант
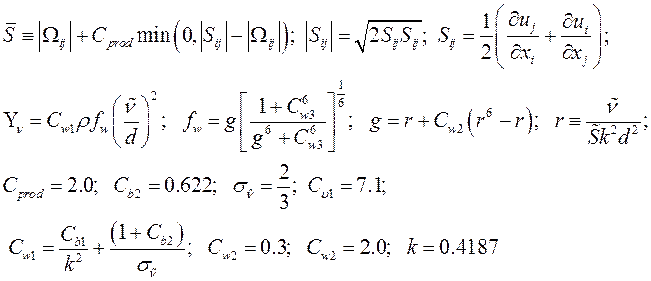
![]() модуль завихренности;
модуль завихренности;
![]() величина модуля тензора скоростей деформации.
величина модуля тензора скоростей деформации.
Для расчета акустического давления использовалась аналогия Керла:
 . (4)
. (4)
Где ![]() – скорость звука,
– скорость звука, ![]() – расстояние до слушателя,
– расстояние до слушателя, ![]() – аэродинамическая сила.
– аэродинамическая сила.
Данная аналогия успешно применялась для решения различных тестовых задач совместно с решателями в составе пакета OpenFOAM. Аналогия Керла позволяет определять акустический шум в ближнем и дальнем полях. Из результатов эксперимента известно, что для многих интересных с практической точки зрения случаев безразмерные частоты шума лежат в диапазоне 0.1 < St < 2, поэтому допущение о компактности акустической аналогии приемлемо [1]. Для учета трехмерных эффектов в двумерной постановке необходимо введение в акустическую аналогию поправки флуктуации в продольном направлении. Для расчета значения уровня звукового давления SPL (SoundPressureLevel) использовалась формула
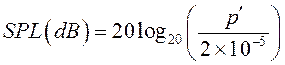 . (5)
. (5)
3. Описание тестовых задач.
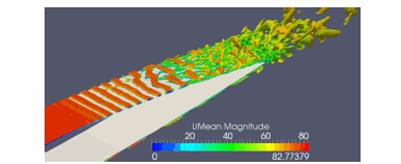
В вычислительной аэроакустике существует набор тестовых задач, которые были выбраны специалистами и обсуждались на различных тематических семинарах в разные годы. Для них существует обширный банк экспериментальных данных и результатов вычислительных экспериментов. К таким задачам относятся, в частности, моделирование обтекания профиля крыла, определение шума в выхлопной трубе автомобиля, моделирование обтекания зеркала заднего вида автомобиля. Указанные задачи были также решены с использованием открытого пакета OpenFOAMи разработанной библиотеки libAcoustics. Также проводились поисковые исследования в области моделирования обтекания и генерируемого шума от изолированного профиля и нескольких профилей [6,7], результаты расчетов представлены на рис. 2, 3, расчета обтекания различных тандемных тел [8], расчетная область и геометрия которых представлена на рис. 4, 5.
| ||
|
| б) |
Рис. 2. Профиль крыла: а) скорость; б) спектр шума
|
|
Рис. 3. Два профиля крыльчатки вентилятора
а) Q-изоповерхности; б) спектр шума
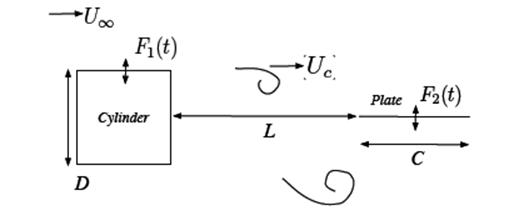
Рис. 4. Прямоугольный цилиндр и пластина
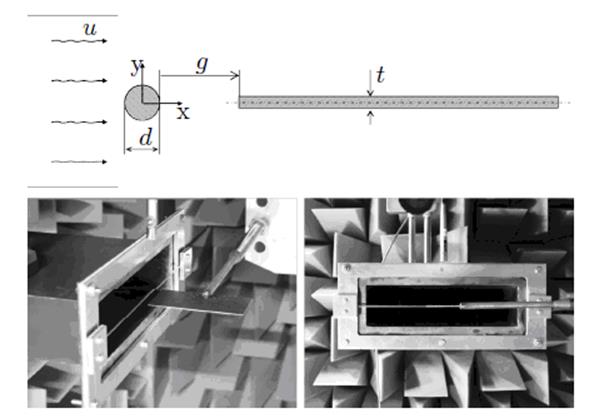
Дополнительно проводились сравнения с результатами экспериментов по значениям уровня звукового давления SPL. Было получено хорошее согласование результатов расчетов и эксперимента.
4. Тестовая задача об обтекании тандема цилиндров.
Рассмотрим более подробно одну из известных тестовых задач вычислительной аэроакустики – задачу о расчете обтекания тандема цилиндров. Соответствующий эксперимент проводился в NASALangleyResearchCenterв BART– BasicResearchAerodynamicTunnel [9]. Данная задача рассматривалась в качестве тестовой во время 1-го семинара BANCWorkshop в г. Стокгольме в 2010 г. и Европейским Концорциумом EUProjectATAAC. Исходные данные для расчетов представлены на рис. 6.
 а)
а) 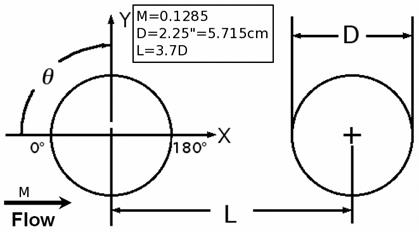 б)
б)
Рис. 6. Танцем цилиндров: a) экспериментальная установка; б) взаимное расположение цилиндров
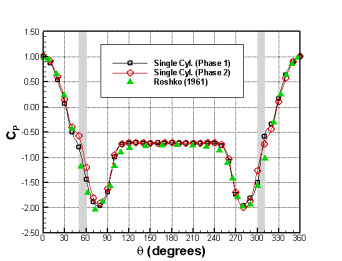
В ходе эксперимента проводилось определение распределения коэффициента давления ![]() по поверхности цилиндров (рис. 7 а, 8) и определение коэффициента продольной силы
по поверхности цилиндров (рис. 7 а, 8) и определение коэффициента продольной силы ![]() (рис. 7 б). Для измерения давления на каждом цилиндре использовалось 22 пьезоэлектрических датчика.
(рис. 7 б). Для измерения давления на каждом цилиндре использовалось 22 пьезоэлектрических датчика.
 а)
а) 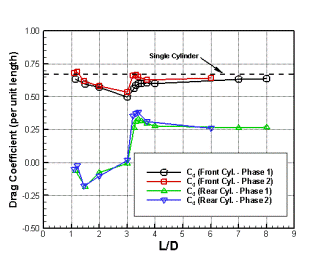 б)
б)
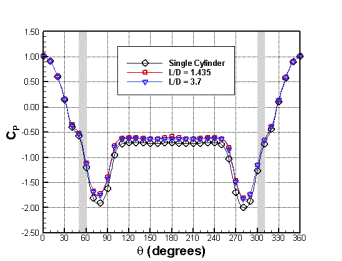
Рис. 7. Коэффициенты: а) давления ![]() ; б) продольной силы
; б) продольной силы ![]()
 а)
а)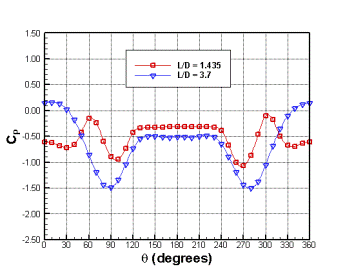 б)
б)
Рис. 8. Коэффициент давления: а) 1 цилиндра; б) 2 цилиндра
С помощью технологии 2D-PIV (ParticleImageVelocimetry) проводилось измерение характеристик потока – линий тока (рис. 9). Для визуализации течения на поверхности цилиндров использовались смесь TiO2 и керосина (рис. 10).
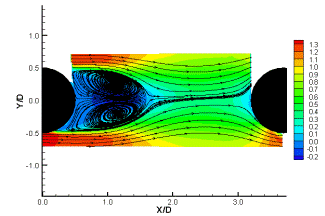

Рис. 9. Линии тока, полученные с 2D-PIV Рис. 10. Визуализация потока
На рисунке 11 изображены спектры пульсации давления для первого и второго цилиндра для разного положения слушателя, связанного с углом ![]() .
.
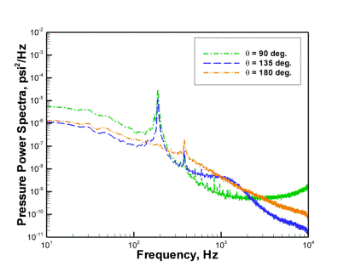 а)
а) 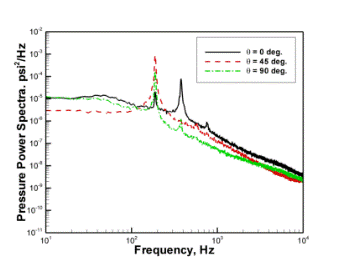 б)
б)
Рис. 11. Спектр пульсации давления а) первого цилиндра; б) второго цилиндра
Отметим, что для данной тестовой задачи помимо результатов натурного эксперимента имеется значительный объем результатов вычислительных экспериментов, проводившихся различными исследователями [10-13]
5. Расчетная схема для проведения вычислительного эксперимента.
При проведении вычислительного эксперимента использовалась двумерная прямоугольная расчетная область с размерами ![]() метра и трехмерная прямоугольная область размерами
метра и трехмерная прямоугольная область размерами ![]() метра. Геометрия расчетной области, обтекаемых цилиндров и адаптивная сетка были построены в пакете Salome. Дополнительно выполнялось сгущение сетки вблизи поверхности цилиндров. Все ячейки сетка являлись гексаэдрами (рис. 12). Общее количество ячеек в двумерном случае составляло 274 000, в трехмерном – 5 480 000. На рис. 12 и 13 представлены расчетная область и фрагменты расчетной сетки в двумерном и трехмерном случае соответственно.
метра. Геометрия расчетной области, обтекаемых цилиндров и адаптивная сетка были построены в пакете Salome. Дополнительно выполнялось сгущение сетки вблизи поверхности цилиндров. Все ячейки сетка являлись гексаэдрами (рис. 12). Общее количество ячеек в двумерном случае составляло 274 000, в трехмерном – 5 480 000. На рис. 12 и 13 представлены расчетная область и фрагменты расчетной сетки в двумерном и трехмерном случае соответственно.


Рис. 12. Расчетная область и фрагменты двумерной расчетной сетки


Рис. 13. Расчетная область и фрагменты трехмерной расчетной сетки
В расчете использовались следующие исходные данные: число Маха ![]() , скорость набегающего потока
, скорость набегающего потока ![]() м/с, число Рейнольдса
м/с, число Рейнольдса ![]() , турбулентная вязкость
, турбулентная вязкость ![]()
![]() . Диаметр цилиндра выбирался равным
. Диаметр цилиндра выбирался равным ![]() м, расстояние между центрами цилиндров
м, расстояние между центрами цилиндров ![]() . В начальный момент времени среда находится в покое, скорость равна 0.
. В начальный момент времени среда находится в покое, скорость равна 0.
Шаг расчета по времени был принят равным ![]() с. Общее время счета составляло 1.5 с. Значения невязок для величин
с. Общее время счета составляло 1.5 с. Значения невязок для величин ![]() полагались равными
полагались равными ![]() , для поправки давления значение невязки выбирались равным
, для поправки давления значение невязки выбирались равным ![]() .
.
Число Куранта не превышало значения ![]() . На входе в расчетную область задавалась скорость набегающего потока
. На входе в расчетную область задавалась скорость набегающего потока ![]() м/с и значения параметров моделей турбулентности исходя из степени турбулентности потока
м/с и значения параметров моделей турбулентности исходя из степени турбулентности потока ![]() = 1%; на выходе – давление; для значений параметров турбулентности на стенках цилиндра использовались пристеночные функции, а также условия прилипания и непротекания. Для дискретизации слагаемых в уравнении (1) использовались различные численные схемы разных порядков точности.
= 1%; на выходе – давление; для значений параметров турбулентности на стенках цилиндра использовались пристеночные функции, а также условия прилипания и непротекания. Для дискретизации слагаемых в уравнении (1) использовались различные численные схемы разных порядков точности.
Для расчета акустического шума задавились дополнительные данные: cкорость звука в воздухе ![]() м/с, расположение слушателей (микрофонов) в точке A с координатами (-0.5223 1.7441 0.1), в точке B с координатами (0.5710 2.032 0.1), в точке С координатами (1.664 2.032 0.1), диапазон вычисляемых частот в Гц.
м/с, расположение слушателей (микрофонов) в точке A с координатами (-0.5223 1.7441 0.1), в точке B с координатами (0.5710 2.032 0.1), в точке С координатами (1.664 2.032 0.1), диапазон вычисляемых частот в Гц.
В процессе расчета целесообразно определить:
а) как влияет дискретизация расчётной области на результат;
б) как влияет дискретизация уравнений (порядок аппроксимации схем) на результат;
в) какое влияние оказывает выбор модели турбулентности;
г) как результат зависит от метода интегрирования уравнений (стационарная или нестационарная постановка задачи).
Результатами вычислительного эксперимента, которые в дальнейшем будут использоваться для сравнения с данными эксперимента являются:
1) коэффициенты продольной силы ![]() первого и второго цилиндра;
первого и второго цилиндра;
2) cпектр частот (в Гц или в безразмерном виде – число Струхаля St);
3) спектр шума (уровень звукового давления SPL).
6. Результаты расчета.
В ходе вычислительного эксперимента была проведена серия расчетов с использованием решателя pisoFoam и моделей турбулентности ![]() ,
, ![]() SST и SA [11], а также метода крупных вихрей LES.
SST и SA [11], а также метода крупных вихрей LES.
Поскольку использовалась акустическая аналогия Кёрла, в которой для расчёта уровня давления фактически входят коэффициенты продольной и нормальной силы, то хорошим критерием проверки на первом этапе может служить сравнение расчётных и экспериментальных значений ![]() (Таблица 2).
(Таблица 2).
Таблица 2. Значения ![]() для физического и численного эксперимента
для физического и численного эксперимента
№ | Источник |
|
|
1 | Расчёт [13] | 0.71 | 0.32 |
2 | Эксперимент (0.68 для одного цилиндра) [7] | 0.62 | 0.32 |
3 | Расчет [12] | 0.4-0.6 | 0.35-0.42 |
4 | Эксперимент [8] | 0.49-0.52 | 0.24-0.35 |
5 | Расчёт[8] | 0.338 | 0.245 |
6 | Эксперимент[14] | 1.2 | |
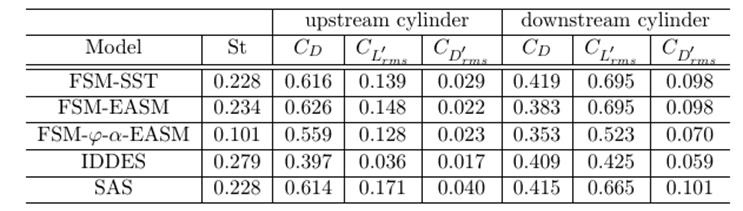
Из таблицы 1 видно, что экспериментальные и расчётные данные имеют существенный разброс даже в средних значениях. Таблица 3 демонстрирует разброс расчетных параметров (число Струхаля, коэффициент продольной силы, коэффициент подъемной силы) в зависимости от выбора модели турбулентности.
Таблица 3. Влияние модели турбулентности на основные параметры
В соответствии с этим был выбран ряд тестовых режимов, которые позволили бы определить степень влияния указанных параметров на расчётную оценку коэффициента продольной силы (Таблица 4).
Таблица 4. Влияние параметров на оценку коэффициента продольной силы
№№ | Описание режима | Cx1 | Cx2 |
| Расчёты с помощью модели SpalartAllmaras с варьированием методов дискретизации уравнений. Использовалась грубая расчётная сетка (№2) с учётом вязкого подслоя с помощью пристеночных функций |
|
|
1. | Название: mesh-2-sa-par Слагаемое по времени — первый порядок (Euler) Конвективные слагаемые — третьего порядка (SFCD) Диффузионные слагаемые — второго порядка (linear) | 0.81 | 0.37 |
2. | Название: mesh-2-sa-par-llinear Слагаемое по времени — первый порядок (Euler) Конвективные слагаемые — второго порядка (limitedLinear) Диффузионные слагаемые — второго порядка (linear) | 0.81 | 0.36 |
3. | Название: mesh-2-sa-par-upwind Слагаемое по времени — первый порядок (Euler) Конвективные слагаемые — первого порядка (upwind) Диффузионные слагаемые — второго порядка (linear) | 0.84 | 0.35 |
4. | Название: mesh-2-sa-par-llinear-bw Слагаемое по времени — второй порядок (backward) Конвективные слагаемые — второго порядка (limitedLinear) Диффузионные слагаемые — второго порядка (linear) | 0.81 | 0.32 |
5. | Название: mesh-2-sa-par-llinear-bw-vl Слагаемое по времени — второй порядок (backward) Конвективные слагаемые — второго порядка (limitedLinear) Диффузионные слагаемые — второго порядка (linear) На поверхности тел модифицированная вязкость задаётся равной 0 | 0.59 | 0.41 |
6. | Название: mesh-2-sa-par-upwind-spalding Слагаемое по времени — первый порядок (Euler) Конвективные слагаемые — первого порядка (upwind) Диффузионные слагаемые — второго порядка (linear) Как вариант №3, но с использованием пристеночных функций Сполдинга | 0.84 | 0.37 |
| Моделирование с помощью моделей k-w SST и k-e |
|
|
7. | Название: mesh-2-sst-par Слагаемое по времени — первый порядок (Euler) Конвективные слагаемые — третьего порядка (SFCD) Диффузионные слагаемые — второго порядка (linear) Используется модель k-w SST | 0.96 | 0.42 |
8. | Название: mesh-2-rho-sst-par Слагаемое по времени — первый порядок (Euler) Конвективные слагаемые — третьего порядка (SFCD) Диффузионные слагаемые — второго порядка (linear) Используется модель k-w SST (как №7, но с учётом сжимаемости) | 1.02 | 0.42 |
9. | Название: mesh-2-ke-par-upwind Слагаемое по времени — первый порядок (Euler) Конвективные слагаемые — первого порядка (upwind) Диффузионные слагаемые — второго порядка (linear) Используется модель k-e | 0.58 | 0.39 |
10. | Название: mesh-2-rho-les-par Слагаемое по времени — первый порядок (Euler) Конвективные слагаемые — третьего порядка (SFCD) Диффузионные слагаемые — второго порядка (linear) Используется LES модель для подсеточной кинетической энергии турбулентности | 1.6 | 0.54 |
| Тестирование сеточной сходимости на модели Spalart-Allmaras с логарифмическими пристеночными функциями. Во всех случаях используется второй порядок дискретизации по пространству и времени. |
|
|
11. | Название: sa-mesh-test/var-1 Грубая сетка, 9650 ячеек | 0.86 | 0.45 |
12. | Название: sa-mesh-test/var-2 Средняя сетка, 13600 ячеек | 0.71 | 0.37 |
13. | Название: sa-mesh-test/var-2 Мелкая сетка, 40000 ячеек | 0.91 | -0.09 |
| Тестирование сеточной сходимости на модели k-e с логарифмическими пристеночными функциями. Во всех случаях используется второй порядок дискретизации по пространству и времени. |
|
|
14. | Название: ke-mesh-test/var-1 Грубая сетка, 9650 ячеек | 0.8 | 0.43 |
15. | Название: ke-mesh-test/var-2 Средняя сетка, 13600 ячеек | 0.54 | 0.41 |
| Тестирование стационарных моделей моделей течения (алгоритм SIMPLE) |
|
|
16. | Название: simple-sa-var-3. Мелкая сетка с пристеночными функциями, модель Spalart-Allmaras, второй порядок точности по пространству | 0.37 | 0.28 |
17. | Название: simple-kw-var-3. Мелкая сетка с пристеночными функциями, модель kw-SST, второй порядок точности по пространству | 0.41 | 0.35 |
18. | Название: simple-sa-upwind-mesh3-lowre Измельченная (504400 элементов) сетка с полным разрешением вязкого подслоя, модель SpalarAllmaras, первый порядок точности для конвективных слагаемых, второй — для диффузионных | 0.71 | 0.2 |
19. | Название: simple-kw-upwind-mesh3-lowre Измельченная (504400 элементов) сетка с полным разрешением вязкого подслоя, модель k-w SST, первый порядок точности для конвективных слагаемых, второй — для диффузионных | 0.58 | 0.2 |
20. | Название: simple-ke-upwind-mesh3-lowre Измельченная (504400 элементов) сетка с полным разрешением вязкого подслоя, модель k-e , первый порядок точности для конвективных слагаемых, второй — для диффузионных | 0.95 | 0.18 |
В процессе предварительных исследований были также определены и анализировались значения модуля скорости и турбулентной вязкости (Рис. 14).
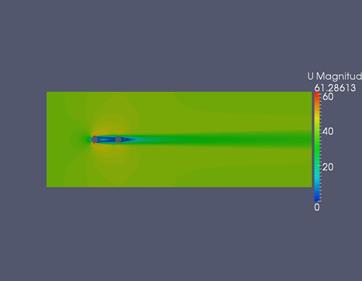 а)
а) 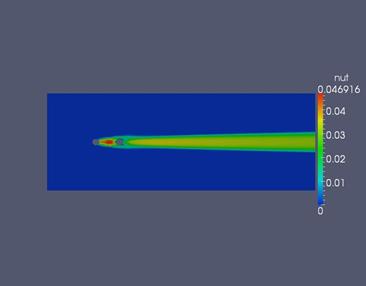 б)
б)
Рис. 14. Визуализация результатов расчета: а) модуль скорости; б) турбулентная вязкость
Как следует из приведённых выше предварительных результатов, параметры расчётной сетки и дискретизации оказывают значительное влияние в первую очередь на коэффициент продольной силы первого цилиндра, в то время как коэффициент продольной силы второго цилиндра остаётся примерно на одном и том же уровне. Результаты, получаемые с помощью стационарных моделей с пристеночными функциями наиболее близки к расчётным данным [10, 11]. Беглый анализ результатов показывает, что при сравнении расчётов с экспериментальными данными необходимо уделять внимание не только настройкам численной модели, но и способам вычисления усреднённой величины исследуемого интегрального параметра. Были построены Qизоповерхности, характеризующие отрывной режим обтекания тандема цилиндров (рис. 15) . На рисунке 16 приведены спектры шума для расчётной модели №4 в точке А. Спектры в других точках отличаются только модулем величины уровня акустического давления.

Рис. 15. Результаты расчета Qизоповерхностей
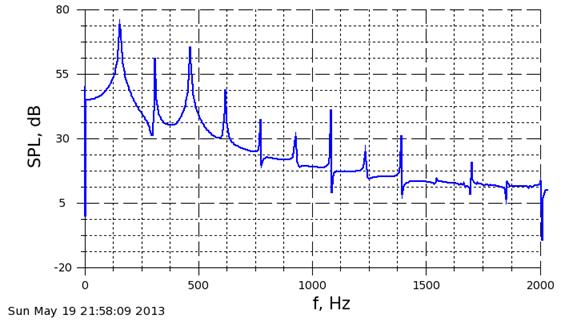
Полученные значение числа Cтрухаля St=0.24 и интенсивности шума для первого пика близки к экспериментальным значениям (Рис. 10).
Заключение
Авторами разработана и реализована в открытом пакете OpenFOAM методика для расчета параметров течения и акустического шума с использованием аналогии Керла. В качестве модельной задачи рассмотрена задача о моделировании обтекания тандема цилиндров и расчета возбуждаемого при этом шума. Результаты численного расчета хорошо согласуются с известными результатами экспериментов, что подтверждает адекватность и эффективность предложенной методики.
В дальнейшем планируется выполнить расчёты в трёхмерной постановке с целью установления степени влияния продольных пульсаций гидродинамических величин на прогнозируемый уровень акустического давления, а также добавить в библиотеку libAcousticsакустическую аналогию Ффоукс– Вильямс – Хоукингса.
Расчеты проводились с использованием вычислительного кластера web-лаборатории UniHUB (www.unihub.ru) в параллельном режиме.
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации.
Список литературы
1. Голдстейн М.Е. Аэроакустика : пер. с англ. М.: Машиностроение, 1981. 294 c.
2. Мунин А.Г., Самохин И.Ф., Шипов Р.А. и др. Авиационная акустика. В 2 ч. Ч. 1. Шум на местности дозвуковых пассажирских самолетов и вертолетов / Под ред. А.Г. Мунина. М. Машиностроение, 1986. 243 с.
3. Wagner C., Hüttl T., Sagaut P. Large–Eddy Simulation for Acoustics. N.Y.: Cambridge Univ. Press, 2007. 471 p.
4. Weller H.G., Tabor G., Jasak H., Fureby C. A tensorial approach to computational continuum mechanics using object oriented techniques // Computers in Physics.1998. Vol. 12, no. 6. P. 620-631.
5. Белов И.А., Исаев С.А. Моделирование турбулентных течений: учеб. пособие. СПб.: БГТУ, 2001. 108 с.
6. Verhoeven O. Trailing Edge Noise Simulations using IDDES in OpenFOAM. Master Thesis. Delft University of Technology. 2011. 139 p.
7. Christophe J., Moreau S., Anthoine J. Trailing Edge Noise Computation of a Fan Blade Profile // 10eme Congres Francais d’Acoustics. Lyon, France. 2010. P. 6.
8. Mohamed Sukri Mat Ali, et al. Aeolian tones generated by a square cylinder with adetached flat plate // 17th AIAA/CEAS Aeroacoustics Conference (32nd AIAA Aeroacoustics Conference), 2011. AIAA 2011-2779. P. 1-20.
9. Jenkins L.N., Neuhart D., McGinley C., Choudhari M., Khorrami M.R. Measurements of Unsteady Wake Interference between Tandem Cylinders // 36th AIAA Fluid Dynamics Conference and Exhibit, 2006. AIAA-2006-3202. P. 1-18.
10. Con J. Doolan. Flow and Noise Simulation of the NASA Tandem Cylinder Experiment using OpenFOAM // 15th AIAA/CEAS Aeroacoustics Conference, 2009. AIAA-2009-3157. P. 1-22.
11. Weinmann M., Sandberg R.D., Doolan C.J. Flow and Noise Predictions for a Tandem Cylinder Configuration Using Novel Hybrid RANS/LES Approaches // 16th CEAS/AIAA Aeroacoustics Conference, Stockholm, Sweden, 2010. AIAA Paper 2010-3787.
12. Weinmann M. Simulation Strategies for Complex Turbulent Flows. PhD Thesis. University of Southampton, October 2011. P. 1-311.
13. Khorrami M.R., Choudhari M.M., Lockard D.P., Jenkins L.N., McGinley C.B. Unsteady Flowfield Around Tandem Cylinders as Prototype Component Interaction in Airframe Noise // AIAA Journal. August 2007. Vol. 45, no. 8. P. 1930-1941.
14. Bruschi G., Nishioka T., Tsang K., Wang R. A Comparison of Analytical Methods. Drag Coefficient of a Cylinder // MAE171A. 2003. Available at: http://www.disasterzone.net/projects/docs/mae171a/water_tunnel_experiment.pdf , accessed 01.08 2013.
Публикации с ключевыми словами: давление, частота, математическая модель, сходимость, спектр, уравнения, модель турбулентности, расчетная область, неструктурированная сетка, цилиндр, акустическая аналогия, метод крупных вихрей
Публикации со словами: давление, частота, математическая модель, сходимость, спектр, уравнения, модель турбулентности, расчетная область, неструктурированная сетка, цилиндр, акустическая аналогия, метод крупных вихрей
Смотри также:
- Выбор аэродинамической компоновки аппарата-зонда, обтекаемого турбулентным закрученным потоком газа
- Экспериментальное и математическое моделирование процесса обтекания летательных аппаратов с тормозными устройствами
- 77-30569/310057 Динамическая диагностическая модель узла крепления обмотки в пазу сердечника статора мощного турбогенератора
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||
 а)
а)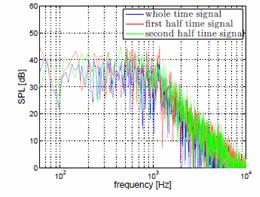
 а
а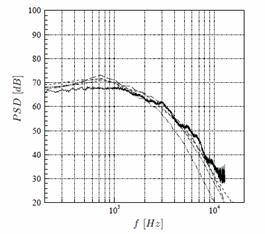 б)
б)