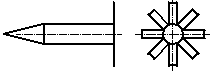научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2012
DOI: 10.7463/1112.0489665
УДК 532.517.4
Россия, МГТУ им. Н.Э. Баумана
Введение
Для торможения и стабилизации при спуске на поверхность планеты спускаемых аппаратов, а также для коррекции по дальности с целью увеличения точности стрельбы артиллерийских снарядов и боевых элементов используются тормозные и управляющие устройства с отклоняющимися «лепестковыми» щитками, предельным вариантом которых является сплошная «юбка» (расширяющийся конус). Обтекание таких органов управлений (ОУ) носит достаточно сложный характер и во многом определяется формой летательного аппарата (ЛА).
На аэродинамические характеристики и структуры обтекания ЛА влияют конструктивные параметры компоновки, такие как форма обтекателя, удлинение корпуса, вид тормозных устройств и.т.д.
Ниже проводятся результаты физического и численного моделирования обтекания цилиндрического тела с различными формами носовой части и конфигурациями тормозного устройства. Определены аэродинамические характеристики ЛА, а также рассмотрено влияние протока между лепестками на распределение давления за донным срезом.
Исследуемые модели экспериментов
Изучаемые аппараты представляли собой комбинацию цилиндрического корпуса, головного обтекателя и тормозных устройств (рисунок 1).
Наиболее простыми тормозными устройствами являются дисковые щитки. Дисковые щитки обеспечивают максимальное тормозное усилие, но структура потока в отрывной зоне имеет склонность к неустойчивости в определенном диапазоне удлинений и чисел Маха. Одним из средств, предотвращающих пульсационные нагрузки, является проток газа из зоны отрыва в донный след через специальные отверстия, или применение лепестковых тормозных устройств. Форма лобового обтекателя также влияет на значение продольного сопротивления.

Рисунок 1 - Исследуемые модели тел:
1 – головной обтекатель; 2 – корпус; 3 – тормозное устройство
Одной из особенностей конструкции щитковых тормозных устройств является наличие протоков между отдельными щитками («лепестками»), обеспечивающих массообмен между зоной отрыва и донным следом. Такой массообмен способствует стабилизации течения в передней отрывной зоне, уменьшению ее размеров, а, следовательно, возрастанию давления на лобовую поверхность щитков. Кроме того, наличие протоков в тормозном стабилизирующем устройстве позволяет устранить пульсационный режим обтекания и обеспечивает выбор b и h, исходя из требуемых тормозных сил. Различные варианты исследуемых щитковых ОУ приведены в таблице 1.
Анализ результатов экспериментального моделирования
Результаты экспериментов позволили установить влияние конструктивных параметров тормозных устройств на аэродинамические коэффициенты и провести сравнительный анализ эффективности различных систем торможения. Исследование аэродинамических характеристик проводилось при числах Маха ![]() =0,81… 5,12, полном давлении
=0,81… 5,12, полном давлении ![]() и температуре T0=260. Все ниже представленные результаты получены для наиболее типичного числа Маха
и температуре T0=260. Все ниже представленные результаты получены для наиболее типичного числа Маха ![]() =2,06.
=2,06.
Результаты экспериментов позволили определить влияние конструктивных параметров тормозных устройств на аэродинамические коэффициенты и провести сравнительный анализ эффективности различных систем торможения.
На рисунке 2 приведенынаиболее типичные аэродинамические характеристики для исследованных вариантов щитков. Коэффициенты ![]() рассчитывали по характерной площади
рассчитывали по характерной площади ![]() , а момент Мz определяли относительно носка ЛА.
, а момент Мz определяли относительно носка ЛА.
На тормозной эффект при обтекании ЛА влияют следующие конструктивные факторы: форма головной части зонда, угол наклона, количество и геометрические размеры (ширина, высота) щитков.
Применение обтекателей с затупленной головной частью (рисунок 2.б), с одной стороны, увеличивает общее сопротивление зонда, но, с другой стороны, из-за образования высокоэнтропийного подслоя с низкими скоростями течения более интенсивно распространяется отрыв перед щитками вверх по потоку, что уменьшает это сопротивление.
При заостренной конической головной части зонда создаются условия обтекания щитков потоком большей энергии вследствие малых потерь полного давления в скачках уплотнения, что уменьшает продольное сопротивление.
Таблица 1 - Основные геометрические параметры моделей.
№ | Схема модели | Количество щитков | Относительная Ширина щитка, | Относительная суммарная площадь протока,
|
1 |
| - | - | 0 |
2 |
| 8 | 0,38 | 0,46 |
3 |
| 6 | 0,38 | 0,6 |
4 |
| 4 | 0,71
| 0,46 |
5 |
| - | - | 0 |
6 |
| 8 | 0,38 | 0,46 |
7 |
| 6 | 0,38 | 0,6 |
8 |
| 4 | 0,71
| 0,46 |
9 |
| - | - | 0 |
10 |
| 8 | 0,38 | 0,46 |
11 |
| 6 | 0,38 | 0,6 |
12 |
| 4 | 0,71
| 0,46 |


а б


в г


д е
Рисунок 2 - Зависимость аэродинамических характеристик Cx, Cy и mz от угла атак
Влияние числа щитков на аэродинамические характеристики исследовалось при условии, что либо неизменной оставалась ширина щитков b (см. таблицу 1 варианты 2, 3), либо их суммарная площадь (варианты 2, 4). В обоих случаях высота щитков была постоянной h=34 мм.
На рисунке 2.а показано, что наличие протока газа в донную область снижает величину коэффициента продольной силы ![]() . Изменение числа щитков в диапазоне N = 6..8 (при одинаковой ширине и длине щитков вариант 2 и 3) и, соответственно, их суммарной площади, на которой создается тормозное усилие, не существенно изменяет продольное сопротивление. Изменение количества щитков при их постоянной суммарной площади (вариант 2 и 4) практически не меняет значение продольного сопротивления.
. Изменение числа щитков в диапазоне N = 6..8 (при одинаковой ширине и длине щитков вариант 2 и 3) и, соответственно, их суммарной площади, на которой создается тормозное усилие, не существенно изменяет продольное сопротивление. Изменение количества щитков при их постоянной суммарной площади (вариант 2 и 4) практически не меняет значение продольного сопротивления.
Математическое моделирование процесса обтекания летательных аппаратов с тормозными устройствами
Особый интерес представляет изменение давления в донной области в рассмотренных экспериментах для различной формы носовой части и тормозных устройств. Это является важным фактом в определение сопротивления ЛА, так как при обтекании тела вращения сверхзвуковым потоком донное сопротивление может составить значительную часть полного аэродинамического сопротивления.
С целью проведения анализа полученных экспериментальных данных и установления влияния форм носовой части и тормозных устройств на донное давление были выполнены численные расчеты в прикладном пакете Ansys 12 (001a922d8114) методом контрольного объема с использованием осредненных уравнений Рейнольдса с замкнутой SST-моделью турбулентности. Исходная система уравнений Навье - Стокса в форме Рейнольдса.
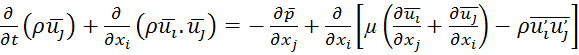 ,
,
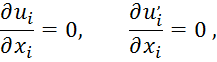
 ,
,
где ![]() - среднее давление;
- среднее давление; ![]() - проекция скорости на оси декартовой системы; индексы i=1,2,3 и j=1,2,3 соответствуют координатам x,y,z;
- проекция скорости на оси декартовой системы; индексы i=1,2,3 и j=1,2,3 соответствуют координатам x,y,z; ![]() - дополнительная вязкость, вызванная пульсациями;
- дополнительная вязкость, вызванная пульсациями; ![]() – символ Кронекера,
– символ Кронекера, ![]() =0 при
=0 при ![]() и 1- при
и 1- при ![]() . Для расчета турбулентных течений с использованием SST модели турбулентности исходная система уравнений замыкалась уравнениями:
. Для расчета турбулентных течений с использованием SST модели турбулентности исходная система уравнений замыкалась уравнениями:
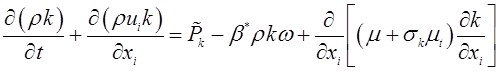

где ![]() - энергия турбулентных пульсаций, удельная скорость диссипации турбулентной энергии, турбулентная вязкость.
- энергия турбулентных пульсаций, удельная скорость диссипации турбулентной энергии, турбулентная вязкость.
![]()
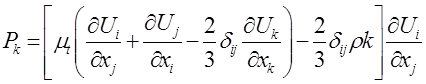



![]()
Константы для модели:
β* =0.09, α1=5/9, β1=3/40, σk1 =0.85, σω1 =0.5, α2=0.44, β2=0.0828, σk2=1, σω2=0.856.
Расчетная область для всех исследуемых конфигураций представляла собой параллелепипед длиной 3L от носовой части до левой границы и 6L от кормового среза до правой границы, высотой 10L и с поперечными размерами 10L. Количество ячеек N≈900 000.
Известно, что при обтекании затупленного тела с иглой сверхзвуковым потоком могут возникать нежелательные пульсации давления в отрывной зоне. Физическая природа пульсаций объясняется неустойчивостью структуры течения и проявляется при отношениях длины иглы h к диаметру тела d, лежащих в диапазоне h/d=2…3. У исследуемых моделей соотношение длины тела к диаметру диска равно 3,15, что режим течения является устойчивым.
Результаты численных расчетов обтекания основных моделей представлены на рисунок 3. Здесь показаны изобары и линия тока.
Сравнительный анализ полученных данных с результатом экспериментальных исследований (рисунок 4) показал их сходимость, что подтверждает адекватность используемого пакета, правильность построения сетки и выбора модели турбулентности.
На рисунок 5 представлена зависимость осредненного относительного давления за донным срезом в ближнем следе ![]() от относительной площади протока через щитки, давление
от относительной площади протока через щитки, давление ![]() определяется по зависимости
определяется по зависимости  . Рассмотрены стабилизующие устройства лепестки типа для которых меняется количество щитков при одной и той же их ширине. Видно что, с увеличением площади протока, осредненное донное давление возрастает.
. Рассмотрены стабилизующие устройства лепестки типа для которых меняется количество щитков при одной и той же их ширине. Видно что, с увеличением площади протока, осредненное донное давление возрастает.
Очевидно, что при обтекании цилиндрических тел, имеющих различные лобовые обтекателя, величина осредненного донного давления




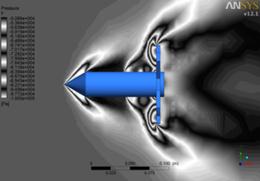




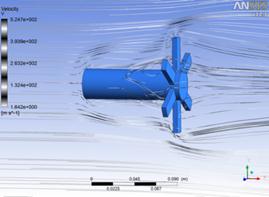
Рисунок 3 - Изобары и линии тока наиболее типичных вариантов
в значительной степеньни зависит от угла раскрытия конуса носовой части. Это связано с чем, что ![]() определяется давлением и числом Маха набегающего потока на цилиндрическом корпусе, которые в свою очередь, зависит от формы носовой части. Чем больше угол раскрытия конуса, тем выше донное давление.
определяется давлением и числом Маха набегающего потока на цилиндрическом корпусе, которые в свою очередь, зависит от формы носовой части. Чем больше угол раскрытия конуса, тем выше донное давление.
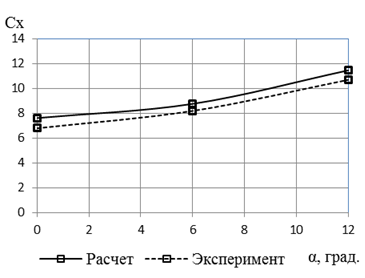

а


б
Рисунок 4 - Зависимость аэродинамических характеристик от угла атаки: а - для модели 1, б - для модели 2.
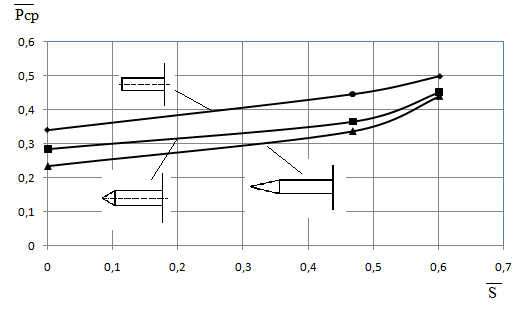
Рисунок 5 - Зависимость среднего донного давления ![]() от относительной площади протока
от относительной площади протока ![]() .
.
Эксперимент и расчет показывал что, при одной и той же площади протока, изменение количества щитков практически не влияет на значение осредненного донного давления, так например при числе Маха ![]() =2,06 для модели 11 с 8 щитками
=2,06 для модели 11 с 8 щитками ![]() =0,42, а для модели 12 с 4 щитками
=0,42, а для модели 12 с 4 щитками ![]() =0,41.
=0,41.
Заключение
На эффект торможения и стабилизации ЛА при ![]() существенные влияния определяются форма носовой части и конструкции тормозного устройства. При увеличении угла полураствора лобового обтекателя, общее сопротивление уменьшает, а осредненное донное давление увеличивает.
существенные влияния определяются форма носовой части и конструкции тормозного устройства. При увеличении угла полураствора лобового обтекателя, общее сопротивление уменьшает, а осредненное донное давление увеличивает.
Наличие протока в стабилизующем устройстве приводит к стабилизации течения в области отрыва перед ним. При этом с увеличением площади протока возрастает донное давление и оно не зависит от количества щитков при одинаковой площади протока.
Список литературы
1. Калугин В. Т. Аэродинамика органов управления полетом летательных аппаратов: учеб. пособие. М.: Изд-во МГТУ им. Н. Э. Баумана, 2004. 688 с.
2. Швец А.И., Швец И.Т. Газодинамика ближнего следа. Киев: Наукова думка, 1976. 382 с.
3. Краснов Н. Ф. Основы аэродинамического расчета. М.: Высшая школа, 1981. 496 с.
4. Чжен П. Управление отрывом потока : Экономичность, эффективность, безопасность : пер. с англ. М.: Мир, 1979. 552 с.
5. Белов И.А., Исаев С.А. Моделирование турбулентных течений: учеб. пособие. Спб.: БГТУ, 2001. 107 с.
6. Ferziger J.H., Peric M. Computational Methods for Fluid Dynamics. Springer-Verlag, Berlin, 2002. 423 p.
7. Weller H.G., Tabor G., Jasak H., Fureby C. A tensorial approach to computational continuum mechanics using object oriented techniques // Computers in Physics. 1998. Vol. 12, no. 6. P. 620-631.
8. Jasak H., Weller H.G., Gosman A.D. High resolution NVD differencing scheme for arbitrarily unstructured meshes // International journal for numerical methods in fluids. 1999. Vol. 31, no. 2. P. 431-449. DOI: 10.1002/(SICI)1097-0363(19990930)31:2<431::AID-FLD884>3.0.CO;2-T
9. ФлетчерК. Вычислительныеметодывдинамикежидкостей. В 2 т. Т.1. Основные положения и общие методы : пер. с англ. М.: Мир, 1991. 504 с.
10. Wyborny W., Kabelitz H.R. Comparison of hypersonic aerodynamic deceleration system based on gun tunnel investigations // AIAA Paper. 1970. No. 1174. 11 p.
Публикации с ключевыми словами: математическая модель, уравнения, модель турбулентности, тормозные устройства, дисковые щитки, донное давление
Публикации со словами: математическая модель, уравнения, модель турбулентности, тормозные устройства, дисковые щитки, донное давление
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||