научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2012
DOI: 10.7463/1012.0461853
УДК 532.517.4
Россия, МГТУ им. Н.Э.Баумана
strijhak@yandex.ru
Введение
Свободное программное обеспечение (СПО) предоставляет широкие возможности для решения задач механики сплошной среды. Альтернатива коммерческим пакетам заключается в использовании и развитии свободного программного обеспечения: открытых пакетов, подобных OpenFOAM (OpenFieldOperationandManipulation), Elmer, Code-Saturne, SALOME, Engrid, Paraview и других. В настоящее время данные пакеты поставляются на условиях GPL (GenericPublicLicense). Их можно загрузить в виде исходные и бинарных кодов из Интернета. Доступность исходного кода позволяет инженерам и исследователям проводить расчеты и разрабатывать собственные решатели.
Открытые коды используют все достоинства объектно-ориентированного программирования и написаны на базе языков программирования C++, Fortran, Python. Как правило, в СПО используется открытый дизайн, проводится разбиение кода на небольшие самостоятельные единицы и проверка их по отдельности. В работе авторами предпринята попытка использования и модификации программного стека на базе пакетов Salome-OpenFOAM-Paraviewдля решения технической задачи в области прикладной аэродинамики. Пакет Salome использовался для построения геометрии и расчетной стеки. В пакете OpenFOAM выполнялось численное моделирование. Пакет Paraviewиспользовался для визуализации результатов расчета. Пакет OpenFOAM является средой программирования для задач механики сплошной среды. OpenFOAM работает с неструктурированными сетками, и допускается использование многогранных ячеек c поддержкой подвижных сеток. В пакете реализована параллельная версия на базе библиотеки OpenMPI и используется метод декомпозиции расчетной области. Пакет предоставляет широкие возможности для моделирования несжимаемых и сжимаемых турбулентных течений жидкости и газа. В частности он может быть применен для решения задач прикладной аэродинамики. В его состав входят 80 различных решателей и 170 утилит. При этом исследователь должен самостоятельно выбирать решатель в зависимости от постановки задачи. Предварительно необходимо провести верификацию решателя с использованием тестовых задач.
Многие технические устройства функционируют в условиях закрученного турбулентного потока. Особенностью их обтекания в закрученном потоке газа является наличие скоса потока и неравномерность профиля продольной составляющей скорости. Это приводит к появлению боковых сил и раскачки, колебаниям обтекаемых устройств относительно места крепления подвески. Например, диагностический аппарат “Сканлайнер” (рис. 1), разработанный для обследования внутренней поверхности дымоотводящих магистралей и движущийся в условиях закрученного потока газа, должен стабилизироваться и иметь амплитуду колебаний не более 5 градусов. На основе эксперимента и численного моделирования для обеспечения требуемой аэродинамической стабилизации была предложена форма с особыми управляющими поверхностями – дисковыми стабилизаторами [1-3]. В литературе вопросу исследования обтекания тела в закрученном потоке уделено незначительное внимание.

Рис. 1. Общий вид диагностического аппарата
Целью работы является апробация расчетной модели, расчет обтекания аппарата-зонда, определение аэродинамических характеристик, сравнение с результатами эксперимента и обоснование выбора аэродинамической компоновки. Научная новизна работы состоит в обосновании выбора оптимальной формы компоновки аппарата-зонда и использовании СПО для решения поставленной задачи.
1. Постановка задачи
Рассмотрена задача о моделировании пространственного течения для случая обтекания цилиндрического тела со стабилизаторами в закрученном дозвуковом потоке несжимаемого газа. Исследуемое тело представляло собой затупленный осесимметричный цилиндр с диаметром ![]() =34 мм и длиной
=34 мм и длиной ![]() =186 мм. Цилиндр может быть без дисков, с одним диском-стабилизатором и с двумя соосными дисками с диаметрами
=186 мм. Цилиндр может быть без дисков, с одним диском-стабилизатором и с двумя соосными дисками с диаметрами ![]() =136 мм,
=136 мм, ![]() =102 мм. Данное тело соответствует уменьшенной модели аппарата “Сканлайнер” и экспериментальной модели для определения аэродинамических характеристик аппарата-зонда в дозвуковой аэродинамической трубе T-500 МГТУ им. Н.Э. Баумана и в установке “винт-кольцо” [2, 3].
=102 мм. Данное тело соответствует уменьшенной модели аппарата “Сканлайнер” и экспериментальной модели для определения аэродинамических характеристик аппарата-зонда в дозвуковой аэродинамической трубе T-500 МГТУ им. Н.Э. Баумана и в установке “винт-кольцо” [2, 3].
Расчетная область представляла собой цилиндр, в центре которой находилось исследуемое тело. Внешние границы расчетной области выбирались достаточно далеко от зон возмущения потока. Границы расчетной области удалены от “носка” исследуемого тела на 10 калибров вверх и вниз по потоку, диаметр расчетной области равен 10 калибрам.Рассматривался вариант расчетной области в форме цилиндра без внешней стенки. Расчеты были выполнены для числа Рейнольдса ![]() , которое соответствовало условиям эксперимента, проведенного в дозвуковой аэродинамической трубе [2]. Для определения числа Рейнольдса в качестве характерного размера выбирался диаметр первого диска
, которое соответствовало условиям эксперимента, проведенного в дозвуковой аэродинамической трубе [2]. Для определения числа Рейнольдса в качестве характерного размера выбирался диаметр первого диска ![]() . Данные, полученные в ходе построения геометрии и сетки для исследуемых областей в пакете Salome, конвертировались c помощью специальной утилиты в формат решателя OpenFOAM. В вычислительном эксперименте использовалась сетка на базе тетраэдров. Использование такой сетки связано со следующими преимуществами:
. Данные, полученные в ходе построения геометрии и сетки для исследуемых областей в пакете Salome, конвертировались c помощью специальной утилиты в формат решателя OpenFOAM. В вычислительном эксперименте использовалась сетка на базе тетраэдров. Использование такой сетки связано со следующими преимуществами:
- сетки хорошо подходят для областей сложной геометрии;
- процесс построения сетки может быть автоматизирован по сравнению с блочными структурированными сетками;
- время построения сетки минимально.
К недостаткам подобных сеток можно отнести:
- тетраэдры не имеют параллельных граней, и это может снижать точность решения;
- требуется гораздо больше расчетных элементов по сравнению с гексаэдральной сеткой;
- сетка должна быть изотропная, соседние элементы должны отличатся незначительно по форме и размерам;
- возникают сложности при интерполяции расчетных данных.
Пограничный слой отдельно не моделировался. Использовалась высокорейнольдсовая модель турбулентности ![]() с пристеночной функцией. Расчеты проводились для нескольких различных вариантов сеток. В результате число ячеек для цилиндрического тела составило 816614, для цилиндра с одним диском 577365 (рис. 3a), для цилиндра с двумя дисками от 315739 до 971823 (рис. 3б). В ходе расчета проводился анализ значения
с пристеночной функцией. Расчеты проводились для нескольких различных вариантов сеток. В результате число ячеек для цилиндрического тела составило 816614, для цилиндра с одним диском 577365 (рис. 3a), для цилиндра с двумя дисками от 315739 до 971823 (рис. 3б). В ходе расчета проводился анализ значения ![]() , которое характеризует ближайшее расстояния от стенки. Где
, которое характеризует ближайшее расстояния от стенки. Где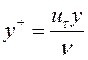 ,
, ![]() - динамическая скорость. Среднее значение
- динамическая скорость. Среднее значение ![]() не превышало 100, что удовлетворяет требованиям для пристеночной функции [4, 5].
не превышало 100, что удовлетворяет требованиям для пристеночной функции [4, 5].
В ходе исследования подготавливался расчетный пример. Задавались начальные и граничные условия. На входной границе задавались граничные условия: модуль вектора скорости с ![]() =25 м/с и условие для закрутки потока. Параметры для выбранной модели турбулентности рассчитывались исходя из степени турбулентности набегающего потока в 1 %, которая соответствует экспериментальной. На стенке задалось условие непротекания. На выходной границе задавалось статическое давление, для остальных величин условия продолжения решения. Расчетная схема имела второй порядок точности по пространству и времени. Для расчета конвективного члена в уравнениях для
=25 м/с и условие для закрутки потока. Параметры для выбранной модели турбулентности рассчитывались исходя из степени турбулентности набегающего потока в 1 %, которая соответствует экспериментальной. На стенке задалось условие непротекания. На выходной границе задавалось статическое давление, для остальных величин условия продолжения решения. Расчетная схема имела второй порядок точности по пространству и времени. Для расчета конвективного члена в уравнениях для ![]() в программе выбиралась схема GaussGamma, для раcчета диффузионного члена использовалась схема Gausslinearcorrected, для величин градиентов
в программе выбиралась схема GaussGamma, для раcчета диффузионного члена использовалась схема Gausslinearcorrected, для величин градиентов ![]() ,
, ![]() схема Gausslinear [6, 7]. Для проведения интерполяции использовалась линейная схема.
схема Gausslinear [6, 7]. Для проведения интерполяции использовалась линейная схема.
Для решения полученных СЛАУ в программе для величин ![]() использовался метод бисопряженных градиентов PBiCG (PreconditionedBiconjugateGradient) с предобуславливателем DILU (DiagonalIncompleteLU) [8], где
использовался метод бисопряженных градиентов PBiCG (PreconditionedBiconjugateGradient) с предобуславливателем DILU (DiagonalIncompleteLU) [8], где ![]() - скорость диссипации турбулентной энергии, тензор рейнольдсовых напряжений, турбулентная вязкость.
- скорость диссипации турбулентной энергии, тензор рейнольдсовых напряжений, турбулентная вязкость.
Для решения уравнения для поправки давления применялся метод PCG (PreconditionedConjugateGradient) с предобуславливателем DIC (DiagonalIncompleteCholesky). Расчетный шаг по времени был равен ![]() секунд. Общее время счета составляло 1-2 секунды. Значения невязок для величин
секунд. Общее время счета составляло 1-2 секунды. Значения невязок для величин ![]() задавались равными
задавались равными ![]() . Для поправки давления значение невязки выбирались
. Для поправки давления значение невязки выбирались ![]() .
.
2. Математическая модель
Расчеты проводились средствами пакета OpenFOAM 1.6, решатель pisoFoam. Математическая модель в pisoFoam основана на решении осредненных по Рейнольдсу уравнений Навье-Стокса, которые замыкаются с помощью различных моделей турбулентности. Обобщенное уравнение, отражающее законы сохранения и модель турбулентности, в интегральной форме выглядит как:

Здесь ![]() - обобщенная переменная
- обобщенная переменная ![]() ;
; ![]() - плотность;
- плотность; ![]() - составляющие скорости вдоль оси 0x, 0y, 0z;
- составляющие скорости вдоль оси 0x, 0y, 0z; ![]() – энтальпия;
– энтальпия; ![]() - контрольный объем;
- контрольный объем; ![]() - вектор скорости;
- вектор скорости; ![]() – вектор площади, совпадающий по направлению с внешней нормалью ячейки;
– вектор площади, совпадающий по направлению с внешней нормалью ячейки; ![]() - коэффициенты переноса;
- коэффициенты переноса; ![]() - источниковый член;
- источниковый член; ![]() - турбулентная кинетическая энергия;
- турбулентная кинетическая энергия; ![]() - удельная скорость диссипации турбулентной энергии;
- удельная скорость диссипации турбулентной энергии; ![]() - полная производная по времени; n – вектор нормали.
- полная производная по времени; n – вектор нормали.
В качестве модели турбулентности использовалась модель ![]() Ментера [4]. Уравнения модели могут быть представлены в следующем виде:
Ментера [4]. Уравнения модели могут быть представлены в следующем виде:

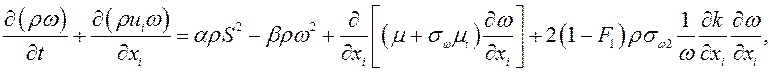
где ![]() - энергия турбулентных пульсаций, удельная скорость диссипации турбулентной энергии, турбулентная вязкость;
- энергия турбулентных пульсаций, удельная скорость диссипации турбулентной энергии, турбулентная вязкость;
![]()

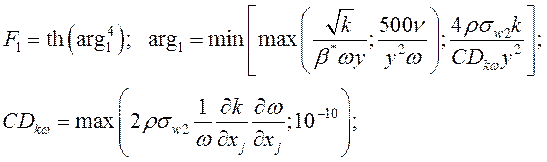

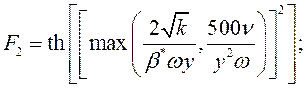
![]()
Приняты следующие значения констант для модели:
β* =0.09; α1=5/9; β1=3/40; σk1 =0.85; σω1 =0.5; α2=0.44; β2=0.0828; σk2=1; σω2=0.856.
Величины ![]() имеют смысл члена генерации энергии турбулентности, тензор скоростей деформации, первой функция смешения, второй функция смешения соответственно.
имеют смысл члена генерации энергии турбулентности, тензор скоростей деформации, первой функция смешения, второй функция смешения соответственно.
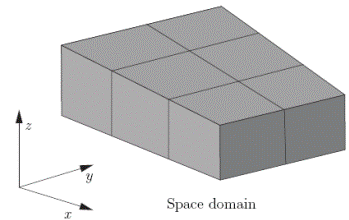
Дискретизация уравнений в OpenFOAM проводилась методом контрольного объема [5, 6]. Расчетная область разбивалась на контрольные объемы. В данном подходе использовалась совмещенная схема расположения узлов, значения скоростей и давления вычисляются в центрах ячеек. Для каждого объема записывались законы сохранения в интегральной форме. Для аппроксимации интегралов использовалась теорема о среднем. В качестве среднего значения по объему принималось значение в центре ячейки, а в качестве среднего значения на грани – значение в центре грани. На рис. 2 представлены расчетная область, система координат и фрагмент расчетной сетки с двумя соседними ячейками.

а) б)
Рис. 2. Система координат и расчетные ячейки
После дискретизации уравнений получалась система линейных алгебраических уравнений (СЛАУ). На данном этапе применялись операции интегрирования, дифференцирования и интерполяции. СЛАУ решались итерационным методом. Полученные уравнения для связи скорости и давления решались итерационным методом PISO. Алгоритм PISO (PressureImplicitwithSplittingofOperators) является эффективным методом решения уравнений Навье-Стокса для нестационарных задач [5]. Основные отличия данного метода от стационарного аналога SIMPLE (Semi-ImplicitMethodforPressure-LinkedEquations) заключаются в следующем:
- не применяются коэффициенты релаксации;
- корректирующий шаг для поправки расчета давления проводится несколько раз.
Алгоритм PISO может быть представлен следующим образом.
1) Постановка граничных условий.
2) Решение дискретизированного уравнения количества движения для получения промежуточного поля скорости.
3) Вычисление массового расхода через грани ячейки.
4) Решение уравнения для поправки давления.
5) Уточнение массового расхода через грани ячейки.
6) Уточнение скоростей на основе нового поля давлений.
7) Обновление граничных условий.
8) Повтор с пункта 3 определенное число раз.
9) Переход к следующему шагу по времени и повтор с пункта 1.
Шаги 4 и 5 могут быть повторены несколько раз для корректировки неортогональности сетки.
3. Методика выполнения расчета
Краткое описание используемого решателя pisoFoam можно представить следующим образом:
1) В исходном коде, написанном на языке программирования C++, сначала приводится заголовок. Заголовок содержит общие сведения, распространяемые на решатель, внутреннее имя решателя и краткое описание. После заголовка следуют директивы подключения используемых библиотечных файлов (модели турбулентности, модели переноса и другие).
2) В теле программы производится инициализация рассчитываемой задачи: задается расположение файлов на диске, считывается и инициализируется расчетная сетка, поля искомых физических величин, подготавливаются счетчики времени и невязки баланса масс. Все эти операции являются стандартными и описаны в библиотечных файлах.
3) После того, как стадия инициализации завершена, начинается интегрирование уравнений во времени. В стационарных решателях вместо времени используется счетчик итераций.
4) Согласно алгоритму PISO производится прогноз поля скоростей по давлению с предыдущего шага и неявная релаксация скорости.
5) Далее строятся соответствующие матрицы и пересчитываются массовые потоки через границы ячеек.
6) В зависимости от заданного числа поправок на неортогональность расчетной сетки производится (nNonOrthCorr+1) шагов, на каждом из которых решается уравнение для давления. По окончании процесса решения вычисляются новые значения массовых потоков, удовлетворяющих уравнению неразрывности.
7) Затем, согласно алгоритму PISO, производится явная релаксация поля давления и коррекция поля скорости.
8) В случае, если течение жидкости неламинарное, то решаются уравнения выбранной модели турбулентности.
9) Выводится информация о затраченном процессором времени на выполнение и производится запись рассчитанных данных на носитель.
10) По окончании процесса интегрирования выводится сообщение об успешном завершении работы, а в операционную систему возвращается код успешного выполнения.
11) В результате решения создаются отдельные папки, которые соответствуют рассчитанным значениям физических величин в различные моменты времени.
Для задания граничного условия для закрутки потока была разработана и внедрена новая служебная утилита “AddSwirlAndRotation”.
4. Результаты расчетов
В работе проведены расчеты для различных тел: цилиндр, цилиндр с одним диском, цилиндр с двумя дисками (рис. 3). Для цилиндра были вычислены аэродинамические характеристики (АДХ) и построены графики их зависимостей от угла атаки.При определении аэродинамических характеристик в качестве характерной площади была выбрана площадь диска с диаметром ![]() , за характерную длину выбрано значение длины модели
, за характерную длину выбрано значение длины модели ![]() . Коэффициент момента тангажа рассчитывался относительно точки подвеса модели на тросе (рис. 1). Полученные АДХ показали, что цилиндрическое тело являлось неустойчивым в потоке относительно точки подвеса.
. Коэффициент момента тангажа рассчитывался относительно точки подвеса модели на тросе (рис. 1). Полученные АДХ показали, что цилиндрическое тело являлось неустойчивым в потоке относительно точки подвеса.
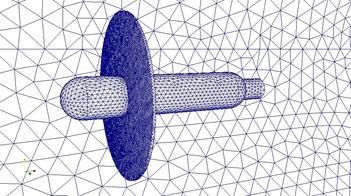
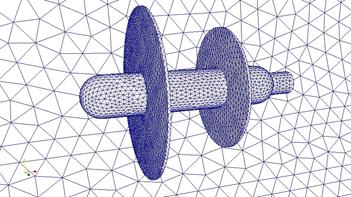
а) б)
Рис. 3. Цилиндр с одним диском (а) и двумя (б) дисками
При увеличении угла атаки увеличивалось значение коэффициент момента тангажа по абсолютному значению (рис. 4). Для случая цилиндра с одним диском оказалось, что зависимость коэффициента момента тангажа ![]() меняла свой знак на противоположный по сравнению со случаем для цилиндра. При этом возникала особенность в диапазоне углов от 0 до 4 градусов. В этом диапазоне значение
меняла свой знак на противоположный по сравнению со случаем для цилиндра. При этом возникала особенность в диапазоне углов от 0 до 4 градусов. В этом диапазоне значение ![]() было близко к нулю. Таким образом, для исследуемого тела стабилизирующий момент отсутствовал. Зависимость
было близко к нулю. Таким образом, для исследуемого тела стабилизирующий момент отсутствовал. Зависимость ![]() была близка к параболической зависимости (рис. 5).
была близка к параболической зависимости (рис. 5).
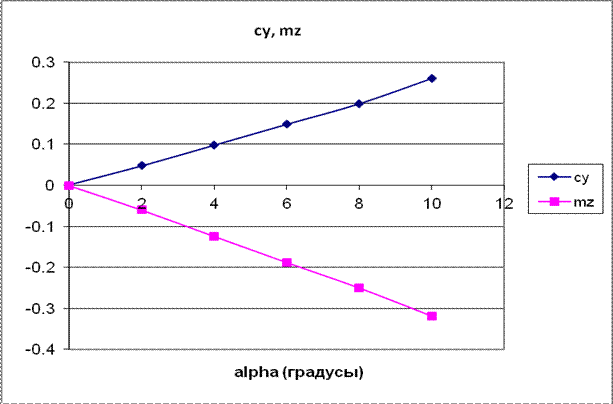
Рис. 4. Зависимость ![]() ,
, ![]() от угла атаки для цилиндра
от угла атаки для цилиндра
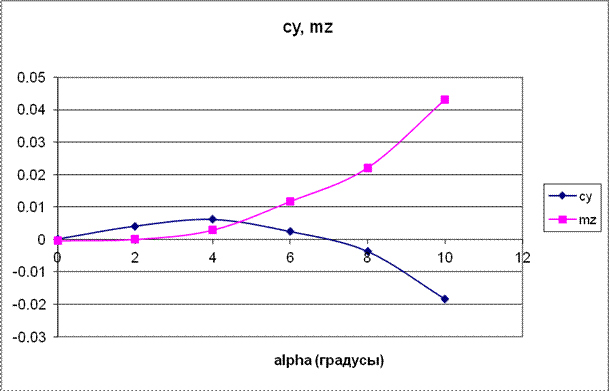
Рис. 5. Зависимость ![]() ,
, ![]() от угла атаки для цилиндра с одним диском
от угла атаки для цилиндра с одним диском
При наличии небольшого возмущения в случае закрутки потока возможно появление раскачки тела на тросе, которое может приводить к возрастанию амплитуды колебаний, превышающей допустимое значение в 5 градусов. Данное явление наблюдалось в эксперименте, проведенном в МГТУ им. Н.Э. Баумана в вертикальной воздуходувке [1,2]. При дальнейшем увеличении угла атаки возникал стабилизирующий момент. Таким образом, можно констатировать, что цилиндр с одним диском-стабилизатором условно устойчив в потоке при увеличении угла атаки. За диском формируется пространственный вихрь (рис. 9).
Аналогичная ситуация возникала при расчете обтекания цилиндра с двумя дисками. В отличие от цилиндра с одним диском, компоновка в форме цилиндр с двумя дисками устойчива во всем диапазоне углов атаки. В диапазоне углов атаки от 0 до 10 градусов зависимость ![]() была близка к линейной (рис. 6). Таким образом, вариант с двумя дисками более предпочтителен по сравнению с одним диском стабилизатором (рис. 7) во всем диапазоне изменения угла атаки.
была близка к линейной (рис. 6). Таким образом, вариант с двумя дисками более предпочтителен по сравнению с одним диском стабилизатором (рис. 7) во всем диапазоне изменения угла атаки.

Рис. 6. Зависимость ![]() ,
, ![]() от угла атаки для цилиндра с двумя дисками.
от угла атаки для цилиндра с двумя дисками.

Рис. 7. Зависимость ![]() от угла атаки для разных тел:
от угла атаки для разных тел:
1 – цилиндр с одним диском, 2 – цилиндр с двумя дисками
Дополнительно были проведены исследования по влиянию размера количества ячеек сетки на результаты значения ![]() (рис. 8) для цилиндра с двумя дисками. Влияние сетки оказалось незначительным и находилось в допустимых пределах 8 %. В дальнейшем расчеты выполнялись только для сетки с 451 478 ячейками.
(рис. 8) для цилиндра с двумя дисками. Влияние сетки оказалось незначительным и находилось в допустимых пределах 8 %. В дальнейшем расчеты выполнялись только для сетки с 451 478 ячейками.

Рис. 8. Зависимость ![]() от угла атаки для различных сеток:
от угла атаки для различных сеток:
1 - 315 739 ячеек; 2 – 451 478 ячеек, 3 – 971 823 ячеек, 4 – 1 014 674 ячеек
На рис. 9 и 10 представлены пространственные линии тока, соответствующие обеканию тел с одним и двумя дисками, как в незакрученном и закрученном потоке. Между дисками и в донной области формируются крупные тороидальные вихри. Данные вихри оказывают стабилизирующее воздействие на положение тела. Получены также распределения давления по поверхности цилиндра с двумя дисками. На переднем диске давление возрастает, в то же время на заднем диске давление существенно падает. Обобщенная аэродинамическая сила направлена вниз. В результате создается стабилизирующий момент относительно точки подвеса. Также возникает дополнительное усилие, направленное вверх по потоку. Результирующая аэродинамическая сила оказывает стабилизирующее воздействие на тело в потоке.

Рис. 9. Результаты расчета обтекания цилиндра с диском. Линии тока. Различным цветом показаны значения величины скорости.

Рис. 10. Результаты расчета обтекания цилиндра с двумя дисками. Линии тока. Различным цветом показаны значения турбулентной вязкости.
С целью определения оптимальной компоновки были проведены параметрические исследования. В ходе исследования изменялось взаимное расположение дисков на цилиндре. Первый диск располагался, как показано на рис. 3. Рассматривалось три различных варианта расположения заднего диска (рис. 11). Были полученные зависимости ![]() , которые являлись практически линейными. Определено, что максимальное значение
, которые являлись практически линейными. Определено, что максимальное значение 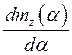 получено для случая, когда диски находятся на минимальном расстоянии друг относительно друга. При этом важно обращать внимание на значение
получено для случая, когда диски находятся на минимальном расстоянии друг относительно друга. При этом важно обращать внимание на значение ![]() . Максимальное значение
. Максимальное значение ![]() =1,25 получено для случая, когда диски находятся на минимальном расстоянии друг относительно друга. Минимальное значение
=1,25 получено для случая, когда диски находятся на минимальном расстоянии друг относительно друга. Минимальное значение ![]() =1,18 получено для случая, когда диски находятся на максимальном расстоянии друг относительно друга. Данный результат может быть использован при проектировании компоновки аппарата-зонда.
=1,18 получено для случая, когда диски находятся на максимальном расстоянии друг относительно друга. Данный результат может быть использован при проектировании компоновки аппарата-зонда.
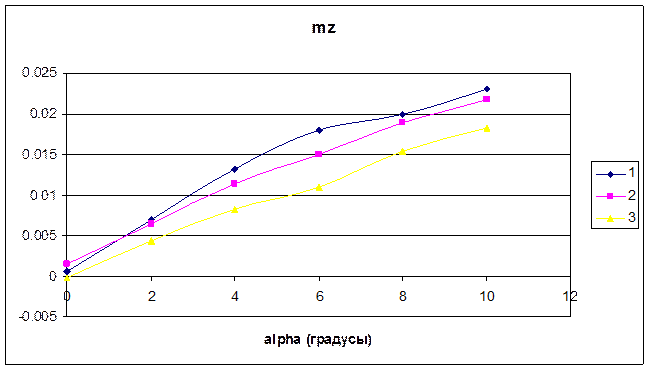
Рис. 11 Зависимость ![]() от угла атаки для различных исследуемых тел.
от угла атаки для различных исследуемых тел.
В качестве тела рассматривался цилиндр с двумя дисками. 1 - Ld/d = 40 мм/ 34 мм; 2 - Ld/d = 70 мм/ 34 мм; 3 - Ld/d = 92 мм/ 34 мм. Ld – расстояние между дисками, d – диаметр основного цилиндра.
Выполнено сравнение по распределению поперечной и продольной компоненты скорости, аэродинамические коэффициенты сравнивались с экспериментальными данными [2,3]. Отличие расчетного значения ![]() составило 5 % от экспериментального. Были построены пространственные линии тока и распределение турбулентной вязкости, которое является самым точным индикатором интенсивного вихреобразования. Также проведены расчеты обтекания тел для случая закрутки потока для случая обтекания цилиндра с двумя дисками при фиксированном положении дисков
составило 5 % от экспериментального. Были построены пространственные линии тока и распределение турбулентной вязкости, которое является самым точным индикатором интенсивного вихреобразования. Также проведены расчеты обтекания тел для случая закрутки потока для случая обтекания цилиндра с двумя дисками при фиксированном положении дисков ![]() =68 мм. Для формирования закрутки потока на входе расчетной области использовалась специально подготовленная служебная утилита “AddSwirlAndRotation”. Закрутка потока задавалась по закону твердого тела. Рассматривались различные значения
=68 мм. Для формирования закрутки потока на входе расчетной области использовалась специально подготовленная служебная утилита “AddSwirlAndRotation”. Закрутка потока задавалась по закону твердого тела. Рассматривались различные значения ![]() =3,10,16,24 рад/c. Оказалось, что закрутка существенно не влияет на значения АДХ для цилиндра с двумя дисками. Сравнение проводилось по значениям
=3,10,16,24 рад/c. Оказалось, что закрутка существенно не влияет на значения АДХ для цилиндра с двумя дисками. Сравнение проводилось по значениям ![]() и
и ![]() . Компоновка в форме цилиндр с двумя дисками была устойчива во всем диапазоне углов атаки от 0 до 10 градусов при наличии закрутки.
. Компоновка в форме цилиндр с двумя дисками была устойчива во всем диапазоне углов атаки от 0 до 10 градусов при наличии закрутки.
Расчеты были выполнены с использованием ресурсов вычислительных кластеров ТТИ ЮФУ (г. Таганрог) и web-лаборатории UniHUB(www.unihub.ru). Для расчетов использовались 16-64 вычислительных ядра в зависимости от расчетной модели и размерности сетки. Время счета составило на 32 ядрах – 17 часов, время счета на 48 ядрах – 12 часов для случая тела – цилиндр. Для случая цилиндра с двумя дисками расчеты выполнялись за 2-3 часа на 16-32 ядрах. Существует возможность решения задач и на более подробных сетках.
5. Заключение
В результате расчета получены поля скоростей, давления, кинетической энергии турбулентности, турбулентной вязкости. Определены значения аэродинамических коэффициентов ![]() в зависимости от угла атаки в диапазоне от 0 до10 градусов для случая незакрученного и закрученного потока.
в зависимости от угла атаки в диапазоне от 0 до10 градусов для случая незакрученного и закрученного потока.
Результаты расчета АДХ и данные экспериментов в МГТУ им. Н.Э. Баумана отличались на 5 %, что является допустимым значением для проведения инженерных расчетов [2, 3]. Модельное тело, представляющее собой цилиндр с двумя дисками, является наиболее устойчивым в потоке при изменении угла атаки и наличии закрутки потока. В результате может быть дана рекомендация по геометрическим параметрам. Оптимальным вариантом с точки зрения аэродинамической стабилизации и минимального сопротивления является компоновка аппарата-зонда при взаимном расположении дисков с диаметрами ![]() =136 – 160 мм,
=136 – 160 мм, ![]() =102 мм на расстояние
=102 мм на расстояние ![]() = 92 мм. На основании этих геометрических параметров могут быть даны рекомендации по расположению дисков-стабилизаторов на промышленном аппарате “Сканлайнер”.
= 92 мм. На основании этих геометрических параметров могут быть даны рекомендации по расположению дисков-стабилизаторов на промышленном аппарате “Сканлайнер”.
Работа выполнена при финансовой поддержке гранта ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы», ГК № 07.514.11.4119 от 02 ноября 2011 года. Работа проводится при поддержке программы «Университетский кластер» (http://www.unicluster.ru).
Список литературы
[1] Беляков В.Н., Калугин В.Т., Сущев С.П. и др. Диагностический комплекс “Сканлайнер” для обследования футеровки дымовых труб без остановки технологических процессов // Конверсия в машиностроении. 2002. № 1. С. 60-66.
[2] Калугин В.Т., Стрижак С.В., Сущев С.П. Аэродинамическая стабилизация диагностического комплекса “Сканлайнер” // Известия РАН. Проблемы машиностроения и надежности машин. 2006. № 3. С. 87-94.
[3] Калугин В.Т., Стрижак С.В. Физическое и математическое моделирование отрывного обтекания аппарата-зонда с дисковыми стабилизаторами в закрученном потоке газа // Научный Вестник МГТУ ГА. Cер. Аэромеханика и прочность. 2008. № 125. С. 63-67.
[4] Белов И.А., Исаев С.А. Моделирование турбулентных течений : учеб. пособие. Спб: БГТУ, 2001. 107 с.
[5] Ferziger J.H., Peric M. Computational Methods for Fluid Dynamics. Springer-Verlag, Berlin, 2002. 423 p.
[6] Weller H.G., Tabor G., Jasak H., Fureby C. A tensorial approach to computational continuum mechanics using object oriented techniques // Computers in Physics. 1998. Vol. 12, no. 6. P. 620-631.
[7] Jasak H., Weller H.G., Gosman A.D. High resolution NVD differencing scheme for arbitrarily unstructured meshes // Int. J. Numer. Meth. Fluids. 1999. Vol. 31. P. 431-449.
[8] Флетчер К. Вычислительные методы в динамике жидкостей. В 2 т. Т.1. Основные положения и общие методы : пер. с англ.- М.: Мир, 1991. 504 с. [Fletcher C.A.J. Computational Techniques for Fluid Dynamics. In 2 vols. Vol. 1. Fundamental and General Techniques. Springer-Verlag, Berlin, 1988.].
Публикации с ключевыми словами: угловая скорость, математическая модель, сходимость, компоновка, уравнения, модель турбулентности, расчетная область, неструктурированная сетка, закрученный поток, угол атаки, аэродинамические коэффициенты, стабилизирующий момент
Публикации со словами: угловая скорость, математическая модель, сходимость, компоновка, уравнения, модель турбулентности, расчетная область, неструктурированная сетка, закрученный поток, угол атаки, аэродинамические коэффициенты, стабилизирующий момент
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



