научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 02, февраль 2012
УДК. 62-26
МГТУ им. Н.Э. Баумана
Введение
На работающем мощном генераторе динамические процессы в дефектных (ослабленных) узлах креплений элементов статора сопровождаются появлением паразитных вибрационных и ударных нагрузок, возбуждающих виброакустические колебания конструкции статора. Определение параметров этих нагрузок является необходимым условием проведения имитационного моделирования вынужденных реакций конструкции статора для ответа на вопрос о возможности их спектрального обнаружения на удаленных элементах конструкции статора и построения алгоритмов диагностирования формализованным методом.
Настоящая работа посвящена разработке динамической диагностической модели узла крепления обмотки в пазовой части сердечника статора мощного турбогенератора с целью изучения динамики незакрепленного участка стержня обмотки и определения возможных значений параметров ударных нагрузок, возбуждающих виброакустические колебания конструкции статора.
1. Статорная обмотка мощных турбогенераторов
Статорная обмотка большинства турбогенераторов представляет собой двухслойную петлевую систему стержневого типа с соединением фаз звезда или двойная звезда. В пазах сердечника статора укладываются один над другим по два стержня, соединяемые с другими стержнями в головках лобовых частей с помощью наконечников и пайки. Ко дну паза стержни прижимаются с помощью распорных пазовых клиньев (рис. 1).
Исправное состояние крепления обмотки в пазовой части характеризуется такой прочностью и плотностью крепления, при которой достигается максимальное ограничение перемещений обмотки внутри паза и стабильность свойств ее крепления в процессе эксплуатации генератора.
Дефектное состояние характеризуется таким ослаблением плотности крепления обмотки, при котором на работающем генераторе возникают радиальные и тангенциальные смещения стержней обмотки в пределах зазоров между стержнями, стержнем и пазовым клином, стержнем и стенками паза, стержнем и дном паза.
Обмотка статора мощного турбогенератора вместе с элементами ее крепления представляет собой весьма сложную электромеханическую систему, точное теоретическое описание динамики которой затруднено следующими факторами [1; 2]:
- стержни обмотки существенно неоднородны: состоят из сплошных и полых медных проводников, покрытых термореактивной изоляцией;
- механические свойства стержней обмотки зависят от нагрузки генератора, длины и температуры;
- способам закрепления стержней обмотки присуща неопределенность связи между собой и с элементами крепления.
«Нестабильность закрепления обмотки статора в процессе эксплуатации, наличие радиальных и тангенциальных зазоров приводит к тому, что условия закрепления стержня оказываются неопределенными, длина незакрепленного участка является случайной величиной, характер закрепления по краям участка также случаен.» [3]. Все это делает возможным лишь безотносительное моделирование динамики дефектного узла крепления обмотки. Структурными параметрами дефекта являются: длина ![]() незакрепленного участка стержня, граничные условия закрепления, величина радиальных и тангенциальных зазоров.
незакрепленного участка стержня, граничные условия закрепления, величина радиальных и тангенциальных зазоров.
2. Математическая модель динамики стержня обмотки в пазу сердечника статора
Рассмотрим упрощенную схему дефектного узла крепления обмотки, представленную на рис. 1. В ней нижний стержень лежит на дне паза и хорошо уплотнен боковыми полупроводящими гофрированными прокладками из стеклотекстолита. На участке длиной ![]() между верхним стержнем и пазовыми клиньями, а также между стержнями имеется распределенный радиальный зазор, величина которого зависит от начальной кривизны верхнего стержня, усадки изоляции в пазах и степени износа соприкасаемых поверхностей. Боковой зазор между верхним стержнем и боковыми поверхностями паза полагаем равным нулю. Зазор между пазовыми клиньями и верхним стержнем считаем достаточно большим, чтобы между ними не происходили соударения. Стержни паза считаем принадлежащими одной фазе. Вибрациями нижнего стержня на дне паза пренебрегаем.
между верхним стержнем и пазовыми клиньями, а также между стержнями имеется распределенный радиальный зазор, величина которого зависит от начальной кривизны верхнего стержня, усадки изоляции в пазах и степени износа соприкасаемых поверхностей. Боковой зазор между верхним стержнем и боковыми поверхностями паза полагаем равным нулю. Зазор между пазовыми клиньями и верхним стержнем считаем достаточно большим, чтобы между ними не происходили соударения. Стержни паза считаем принадлежащими одной фазе. Вибрациями нижнего стержня на дне паза пренебрегаем.
Описание динамики верхнего стержня проведем в рамках модели деформируемого (упругого) тела - тонкого прямого призматического стержня, для которого выполняется гипотеза плоских сечений. В практически важных случаях квадрат отношения высоты стержня к его пролету всегда существенно меньше единицы: ![]() . Поэтому распределение напряжений и деформаций, создаваемых в стержне, примем такими же, как это предписывается элементарной теорией изгиба. Зависимостью граничных условий и изгибной жесткости стержня от длины, температуры и возмущающих сил, а также случайным характером закрепления в процессе эксплуатации пренебрегаем.
. Поэтому распределение напряжений и деформаций, создаваемых в стержне, примем такими же, как это предписывается элементарной теорией изгиба. Зависимостью граничных условий и изгибной жесткости стержня от длины, температуры и возмущающих сил, а также случайным характером закрепления в процессе эксплуатации пренебрегаем.

Рис. 1. Схема дефектного узла крепления обмотки в пазу сердечника статора мощного турбогенератора: 1 - пазовый клин; 2- прокладка под клин (стеклотекстолит); 3 - верхний стержень; 4 – прокладка между стержнями (стеклотекстолит); 5 - нижний стержень, 6 – прокладка на дне паза (электронит), 7 – сердечник статора, 8 – радиальные зазоры.
Расчетная схема рассматриваемой распределенной виброударной системы (ВУС) «обмотка – сердечник» представлена на рис. 2. В ней введена правая система координат, ось ![]() направлена по центральной оси верхнего стержня, а плоскость
направлена по центральной оси верхнего стержня, а плоскость ![]() является нейтральной плоскостью стержня при симметричном изгибе. Обозначим через
является нейтральной плоскостью стержня при симметричном изгибе. Обозначим через ![]() – перемещение точек центральной оси стержня относительно недеформированного состояния;
– перемещение точек центральной оси стержня относительно недеформированного состояния; ![]() - эквивалентную изгибную жесткость стержня при колебаниях;
- эквивалентную изгибную жесткость стержня при колебаниях; ![]() - массу единицы длины стержня. Концы стержня полагаем жестко защемленными неподвижными опорами. Распределенную величину зазора между стержнями определим симметричной функцией
- массу единицы длины стержня. Концы стержня полагаем жестко защемленными неподвижными опорами. Распределенную величину зазора между стержнями определим симметричной функцией
 , (1)
, (1)
где ![]() - максимальное значение зазора в сечении
- максимальное значение зазора в сечении ![]() . Уравнение (1) совпадает со статической кривой изгиба стержня с жестко заделанными концами, повернутыми на угол
. Уравнение (1) совпадает со статической кривой изгиба стержня с жестко заделанными концами, повернутыми на угол ![]() [4].
[4].
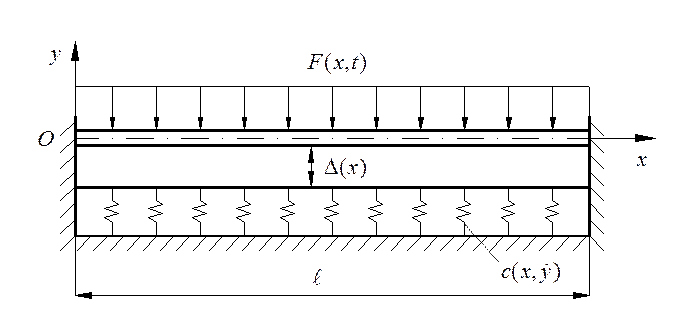
Рис. 2. Расчетная динамическая схема ВУС «обмотка – сердечник»
Рассмотрим внешне силы, возбуждающие колебания стержней обмотки в пазовой части. «В пазовой части основную роль играет радиальное усилие, возникающее в результате взаимодействия токов в стержнях и влияния сердечника статора. Оно пропорционально квадрату тока стержня и максимально для верхнего стержня. Имеется также тангенциальное усилие, вызванное взаимодействием тока в стержнях с потом возбуждения, но оно не велико из-за экранирующего действия стали зубцов» [3].
В рамках диагностического моделирования динамики дефектного узла крепления обмотки учтем основное радиальное электродинамическое усилие. Влиянием тангенциального усилия и магнитных вибраций сердечника на колебания стержней обмотки в пазовой части пренебрегаем.
В проекции на ось ![]() распределенное радиальное электродинамическое усилие, действующее на верхний стержень, имеет вид (рис.2) [3]
распределенное радиальное электродинамическое усилие, действующее на верхний стержень, имеет вид (рис.2) [3]
![]() , (2)
, (2)
где
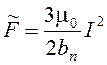 . (3)
. (3)
Здесь ![]() - амплитуда знакопеременной составляющей усилия при синфазном токе в стержнях обмотки, Н/м,
- амплитуда знакопеременной составляющей усилия при синфазном токе в стержнях обмотки, Н/м, ![]() Гн/м – магнитная проницаемость воздуха,
Гн/м – магнитная проницаемость воздуха, ![]() - действующее значение тока в стержне, А,
- действующее значение тока в стержне, А, ![]() - ширина паза в свету, м,
- ширина паза в свету, м, ![]() - номинальная угловая частота тока, равная
- номинальная угловая частота тока, равная ![]() рад/c. При синфазном токе в стержнях радиальное усилие на нижний стержень в 3 раза меньше (3) [3]. Оба радиальных усилия направлены ко дну паза.
рад/c. При синфазном токе в стержнях радиальное усилие на нижний стержень в 3 раза меньше (3) [3]. Оба радиальных усилия направлены ко дну паза.
Диссипацию энергии при колебаниях верхнего стержня учтем через действие распределенных сил внешнего и внутреннего вязкого трения. В рамках диагностического моделирования любая разумная гипотеза о распределении сил трения является одинаково приемлемой. Поэтому полагаем, что силы трения распределены таким образом, что главные координаты для консервативной системы являются главными и для системы с трением.
Контактные деформации стержней обмотки при соударениях опишем в рамках модели упругодиссипативного элемента в каждом сечении стержня, а сами деформации отнесем к основанию системы. Динамическую силовую характеристику распределенной ударной пары (упругодиссипативные свойства основания системы) определим выражением (рис. 2)
![]() , (4)
, (4)
где
 (5)
(5)
Здесь ![]() - функция единичного скачка Хэвисайда,
- функция единичного скачка Хэвисайда, ![]() и
и ![]() – коэффициенты погонной жесткости основания на этапе нагрузки и разгрузки соответственно, H/м2, связанные между собой соотношением
– коэффициенты погонной жесткости основания на этапе нагрузки и разгрузки соответственно, H/м2, связанные между собой соотношением
![]() , (6)
, (6)
где ![]() .
.
С увеличением поверхности контакта жесткость динамической силовой характеристики распределенной ударной пары увеличивается и достигает своего максимума при распределенном ударе по всей длине стержня.
Момент отрыва (окончания удара) в произвольном сечении стержня определяется геометрическим условием
![]() . (7)
. (7)
С учетом сделанных допущений дифференциальное уравнение изгибных колебаний стержня с граничными и начальными условиями имеет вид
 ; (8)
; (8)
![]() ,
, ![]() ,
, ![]() ,
, ![]() ; (9)
; (9)
![]() ,
, ![]() . (10)
. (10)
Здесь ![]() и
и ![]() - коэффициенты внешнего и внутреннего вязкого трения соответственно.
- коэффициенты внешнего и внутреннего вязкого трения соответственно.
Воспользуемся методом Бубнова-Галеркина [5] для нахождения приближенного решения дифференциального уравнения (8) в виде сходящегося ряда ортогональных функций
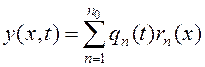 , (11)
, (11)
удовлетворяющих всем граничным условиям. Здесь ![]() - обобщенная координата (функция времени), зависящая от начальных условий и внешних сил;
- обобщенная координата (функция времени), зависящая от начальных условий и внешних сил; ![]() -
- ![]() -я форма собственных колебаний стержня без учета демпфирования, удовлетворяющая дифференциальному уравнению
-я форма собственных колебаний стержня без учета демпфирования, удовлетворяющая дифференциальному уравнению
 , (12)
, (12)
 , (13)
, (13)
и граничным условиям (9), которые запишем в виде
![]() ,
, ![]() ,
, ![]() ,
, ![]() . (14)
. (14)
Здесь ![]() -
- ![]() -я собственная частота консервативной системы.
-я собственная частота консервативной системы.
Решение дифференциального уравнения (12) с граничными условиями (14) имеет вид [4]
![]() , (15)
, (15)
 , (16)
, (16)
где
![]() 4,730,
4,730, ![]() 7,853,
7,853,  ,
, ![]() (17)
(17)
- ненулевые значения корней частотного уравнения
![]() . (18)
. (18)
Коэффициенты ![]() выбраны так, что
выбраны так, что
 . (19)
. (19)
Подставляя выражение (11) в уравнение (8) и принимая во внимание, что
![]() ,
,
получим
 . (20)
. (20)
Знак неравенства в (20) объясняется тем, что выражение (11) не является точным (ограниченный ряд). Умножим выражение (20) на каждую из координатных функций ![]() , затем проинтегрируем по длине стержня и приравняем нулю (усредняем ошибки, внесенные выражением (11), по всей длине стержня)
, затем проинтегрируем по длине стержня и приравняем нулю (усредняем ошибки, внесенные выражением (11), по всей длине стержня)
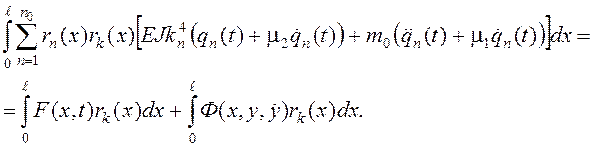 (21)
(21)
С учетом выражения (4) второй интеграл в правой части уравнения (21) принимает вид
 (22)
(22)
Анализ интегро-дифференциального уравнения (21) показывает, что на этапах безударного движения (![]() =0) и распределенного удара по всей длине стержня (
=0) и распределенного удара по всей длине стержня (![]() 0 для
0 для ![]() ) функции времени
) функции времени ![]() являются независимыми. При соударениях части сечений стержня, интеграл от функции
являются независимыми. При соударениях части сечений стержня, интеграл от функции ![]() в (22) зависит от всех функций времени
в (22) зависит от всех функций времени ![]() и не позволяет получить из (21) систему независимых дифференциальных уравнений относительно
и не позволяет получить из (21) систему независимых дифференциальных уравнений относительно ![]() . Поэтому решение интегро - дифференциального уравнения (20) будем искать численно методом припасовывания на малых интервалах времени
. Поэтому решение интегро - дифференциального уравнения (20) будем искать численно методом припасовывания на малых интервалах времени ![]() , заменяя в выражении (22) переменные функции
, заменяя в выражении (22) переменные функции ![]() и
и ![]() на
на ![]() -м шаге по времени постоянными величинами
-м шаге по времени постоянными величинами ![]() и
и ![]() , определенными на предыдущем (
, определенными на предыдущем (![]() ) шаге. Перемещения и скорости в конце
) шаге. Перемещения и скорости в конце ![]() - го шага служат начальными условиями для перемещения и скорости в начале
- го шага служат начальными условиями для перемещения и скорости в начале ![]() - го шага.
- го шага.
С учетом выражения (19) и свойства ортогональности собственных форм колебаний ![]() , получаем, что на малых интервалах времени
, получаем, что на малых интервалах времени ![]() уравнение (21) приводится к системе
уравнение (21) приводится к системе ![]() приближенных несвязанных обыкновенных дифференциальных уравнений функций времени
приближенных несвязанных обыкновенных дифференциальных уравнений функций времени ![]() с постоянными коэффициентами, которые в данном случае будут нормальными координатами:
с постоянными коэффициентами, которые в данном случае будут нормальными координатами:
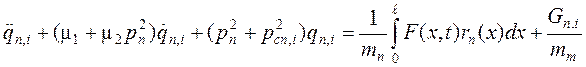 ,
,![]() , (23)
, (23)
где
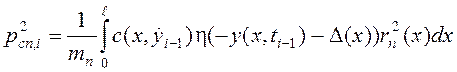 , (24)
, (24)
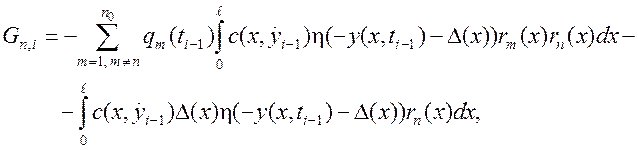 (25)
(25)
 . (26)
. (26)
Здесь ![]() ,
, ![]() - величины, постоянные на
- величины, постоянные на ![]() - м шаге по времени,
- м шаге по времени, ![]() - приведенная масса стержня при колебаниях по
- приведенная масса стержня при колебаниях по ![]() - му тону,
- му тону, ![]() - текущий момент времени.
- текущий момент времени.
Подставляя выражение (2) в уравнение (23), запишем его в стандартном виде
 ,
, ![]() , (27)
, (27)
где
![]() ,
,
![]() ,
,
 .
.
Здесь ![]() - коэффициент демпфирования по
- коэффициент демпфирования по ![]() - й форме;
- й форме; ![]() - собственная частота колебаний стержня;
- собственная частота колебаний стержня; ![]() - обобщенная внешняя сила. Величины
- обобщенная внешняя сила. Величины ![]() и
и ![]() постоянные на
постоянные на ![]() - м шаге по времени. На этапах безударного движения
- м шаге по времени. На этапах безударного движения ![]() 0,
0, ![]() 0.
0.
В силу симметрии рассматриваемой ВУС равнодействующая распределенной ударной силы (4) приложена в середине стержня. Ее значения в моменты времени ![]() рассчитываются по формуле
рассчитываются по формуле
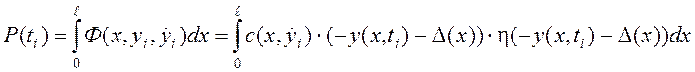 . (28)
. (28)
В слабо демпфированных системах, к которым относятся незакрепленные участки элементов статора, еще недостаточно изучена сама природа явления демпфирования. Поэтому значения относительного демпфирования нормальных форм колебаний [4]
 (29)
(29)
удобнее получать из экспериментов, например, по параметрам ![]() и
и ![]() частотных характеристик незакрепленных элементов статора.
частотных характеристик незакрепленных элементов статора.
Анализ выражения (29) показывает, что при ![]() ,
, ![]() низшие формы колебаний подавляются сильнее, чем высшие формы, а при
низшие формы колебаний подавляются сильнее, чем высшие формы, а при ![]() ,
, ![]() наоборот высшие формы подавляются сильнее, чем низшие формы.
наоборот высшие формы подавляются сильнее, чем низшие формы.
Экспериментальная оценка значений относительного демпфирования ![]() собственных форм колебаний незакрепленных элементов статора показала, что они достаточно близки между собой. Объясняется это тем, что ни потери на внутреннее трение для большинства материалов, ни конструкционный гистерезис от частоты не зависят [6]. Поэтому в первом приближении можно принять
собственных форм колебаний незакрепленных элементов статора показала, что они достаточно близки между собой. Объясняется это тем, что ни потери на внутреннее трение для большинства материалов, ни конструкционный гистерезис от частоты не зависят [6]. Поэтому в первом приближении можно принять ![]() и определять значения коэффициентов демпфирования по приближенной формуле
и определять значения коэффициентов демпфирования по приближенной формуле
![]() . (30)
. (30)
К слабо демпфированным системам здесь и далее будем относить системы, у которых ![]() [4]. В работе [3] приводятся экспериментальные данные, согласно которым для стержня обмотки в пазовой части минимальные значения относительного демпфирования
[4]. В работе [3] приводятся экспериментальные данные, согласно которым для стержня обмотки в пазовой части минимальные значения относительного демпфирования ![]() (0,013; 0,025).
(0,013; 0,025).
В условиях, когда обобщенные силы заданы, собственные функции и собственные частоты известны, значения коэффициентов демпфирования по формам колебаний и динамические силовые характеристики распределенной ударной пары определены, нелинейное дифференциальное уравнение порогового типа (8) приобретает определенный вид. Его решение на малых интервалах времени ![]() сводится к решению системы
сводится к решению системы ![]() несвязанных линейных дифференциальных уравнений (27) с постоянными коэффициентами. Рекуррентные формулы для вычисления динамических перемещений по
несвязанных линейных дифференциальных уравнений (27) с постоянными коэффициентами. Рекуррентные формулы для вычисления динамических перемещений по ![]() -й форме колебаний стержня с демпфированием в моменты времени
-й форме колебаний стержня с демпфированием в моменты времени ![]() имеют вид [4]
имеют вид [4]
 (31)
(31)
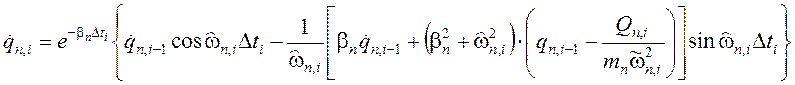 ,(32)
,(32)
- где ![]() и
и ![]() - смещение и скорость смещения нормальных координат в начале рассматриваемого
- смещение и скорость смещения нормальных координат в начале рассматриваемого ![]() - го интервала времени;
- го интервала времени;
![]()
- частота свободных радиальных колебаний стержня по ![]() - й форме с учетом демпфирования. Значения
- й форме с учетом демпфирования. Значения ![]() и
и ![]() служат начальными условиями для следующего
служат начальными условиями для следующего ![]() шага.
шага.
3. Определение параметров виброударной системы «обмотка – сердечник»
Согласно справочным данным [7] удельные массы ![]() стержней статорных обмоток мощных турбогенераторов серии ТВВ отличаются не более чем на 40 %, а моменты инерции
стержней статорных обмоток мощных турбогенераторов серии ТВВ отличаются не более чем на 40 %, а моменты инерции ![]() их поперечных сечений - не более чем в 3 раза. Поэтому без нарушения общности получаемых решений анализ динамики ВУС «обмотка – сердечник» проведем на примере статорной обмотки турбогенератора ТВВ-320-2 со следующими близкими к реальным значениям параметрами обмотки (рис.1):
их поперечных сечений - не более чем в 3 раза. Поэтому без нарушения общности получаемых решений анализ динамики ВУС «обмотка – сердечник» проведем на примере статорной обмотки турбогенератора ТВВ-320-2 со следующими близкими к реальным значениям параметрами обмотки (рис.1): ![]() 0,033 м,
0,033 м, ![]() 0,099 м,
0,099 м, ![]() 2,5.1010 Н/м2,
2,5.1010 Н/м2, ![]() 2,66.10-6 м4,
2,66.10-6 м4, ![]() 12,8 кг/м. Ширина паза
12,8 кг/м. Ширина паза ![]() 0,033 м.
0,033 м.
Схема соединения обмотки – двойная звезда. Поэтому максимальное действующее значение синфазного тока в каждом стержне паза ![]() 5,1 кА. Подставляя
5,1 кА. Подставляя ![]() в формулу (3) находим оценку максимального значения амплитуды знакопеременной составляющей электродинамического усилия
в формулу (3) находим оценку максимального значения амплитуды знакопеременной составляющей электродинамического усилия ![]() 1500 Н/м. Номинальная угловая частота тока
1500 Н/м. Номинальная угловая частота тока ![]() рад/c.
рад/c.
Подставляя первый корень (17) частотного уравнения (18) в выражение (13) находим первую критическую длину ![]() стержня, при которой первая собственная частота колебаний стержня
стержня, при которой первая собственная частота колебаний стержня ![]() совпадает с частотой внешней силы
совпадает с частотой внешней силы ![]() (рис. 3,а). Её значение
(рис. 3,а). Её значение ![]() 1,605 м. Согласно выражению (26) приведенные массы
1,605 м. Согласно выражению (26) приведенные массы ![]() всех форм колебаний стержня равны друг другу и линейно зависит от его длины
всех форм колебаний стержня равны друг другу и линейно зависит от его длины ![]() (рис.3,б). При длине стержня
(рис.3,б). При длине стержня ![]() имеем
имеем ![]() = 20,4 кг.
= 20,4 кг.

Рис. 3. Зависимость низшей собственной частоты колебаний стержня (а) и его приведенной массы (б) от длины ![]()
Постоянная составляющая электродинамического усилия (2) направлена ко дну паза и обеспечивает выборку зазора между стержнями. Максимальный статический прогиб стержня возникает в срединном сечении [4]
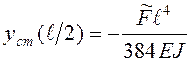 . (33)
. (33)
При ![]() и
и ![]() 1500 Н/м имеем
1500 Н/м имеем ![]() -385 мкм.
-385 мкм.
На этапе нагрузки коэффициент погонной жесткости основания ![]() учитывает контактную жесткость двух стержней обмотки. Поэтому
учитывает контактную жесткость двух стержней обмотки. Поэтому
![]() , (34)
, (34)
где ![]() - эмпирический коэффициент линеаризованной погонной контактной жесткости стержня. На этапе разгрузки коэффициент погонной жесткости основания
- эмпирический коэффициент линеаризованной погонной контактной жесткости стержня. На этапе разгрузки коэффициент погонной жесткости основания ![]() определяется по формуле (6). Экспериментально установлено, при местом смятии стержня до 100 мкм значения
определяется по формуле (6). Экспериментально установлено, при местом смятии стержня до 100 мкм значения ![]() (4,5.108; 4,9.109) Н/м2. Причем, максимальное значение
(4,5.108; 4,9.109) Н/м2. Причем, максимальное значение ![]() несколько меньше теоретического
несколько меньше теоретического
 8,3.109 Н/м2.
8,3.109 Н/м2.
Подставляя эти значения в формулу (34) получаем, что при деформациях основания до 200 мкм значения ![]() (2,25.108; 41,5.108) Н/м2 и
(2,25.108; 41,5.108) Н/м2 и ![]() 1.
1.
Для удобства представления и анализа результатов расчета динамики ВУС в установившихся режимах движения введем следующие расчетные параметры:
· ![]() и
и ![]() - соответственно максимальное положительное и отрицательное значение радиального смещения стержня в сечении
- соответственно максимальное положительное и отрицательное значение радиального смещения стержня в сечении ![]() относительно его недеформированного положения;
относительно его недеформированного положения;
· ![]() - максимальное значение сигнала ударной силы
- максимальное значение сигнала ударной силы ![]() (28);
(28);
· ![]() - амплитудное значение сигнала ударной силы
- амплитудное значение сигнала ударной силы ![]() на частоте вынуждающей электродинамической силы, номинально 100Гц;
на частоте вынуждающей электродинамической силы, номинально 100Гц;
· ![]() - верхняя частота частотного диапазона сигнала ударной силы
- верхняя частота частотного диапазона сигнала ударной силы ![]() , в котором сосредоточено 90% энергии сигнала;
, в котором сосредоточено 90% энергии сигнала;
· ![]() - среднее по реализации стационарного виброударного процесса число соударений за период действия электродинамического усилия, номинально 0,01с;
- среднее по реализации стационарного виброударного процесса число соударений за период действия электродинамического усилия, номинально 0,01с;
· ![]() - среднее квадратическое значение (СКЗ) сигнала ударной силы
- среднее квадратическое значение (СКЗ) сигнала ударной силы ![]() в полосе частот от 200 до
в полосе частот от 200 до ![]() Гц;
Гц;
 , [Н], (35)
, [Н], (35)
где ![]() ,
, ![]() - разрешение по частоте в дискретном спектре
- разрешение по частоте в дискретном спектре ![]() сигнала ударной силы. Здесь
сигнала ударной силы. Здесь ![]() 200 Гц,
200 Гц, ![]() 16 кГц - верхняя частота в спектре сигнала ударной силы.
16 кГц - верхняя частота в спектре сигнала ударной силы.
Для сравнения параметров ударных сил, возникающих при распределенном и сосредоточенном ударе, введем две конфигурации ВУС:
- первая с распределенной ударной парой (РУП) определена в разделе 2, где распределенная величина зазора дается выражением (1);
- вторая с сосредоточенной ударной парой (СУП). Ее конфигурацию определим следующим образом: величина зазора в срединном сечении стержня ![]() , где
, где ![]() 0,06 м равна
0,06 м равна ![]() ; в остальных сечениях стержня зазор между основанием и стержнем превышает возможные деформации последнего.
; в остальных сечениях стержня зазор между основанием и стержнем превышает возможные деформации последнего.
4. Результаты математического моделирования динамики виброударной системы «обмотка – сердечник»
Математическая модель динамики распределенной ВУС «обмотка – сердечник», расчетная схема которой представлена на рис.2, реализована в программе на ПЭВМ и включает в себя 12 независимых структурных и физико - механических параметров. Программа позволяет проводить вычислительные эксперименты по изучению динамики ВУС в переходных и установившихся режимах движения, рассчитывать временные и спектральные параметры сигнала ударной силы, возбуждающей виброакустические колебания конструкции статора при различных значениях структурных и физико - механических параметров системы.
В программе расчет динамики ВУС (решение дифференциального уравнения (8)) ведется численно методом припасовывания по формулам (31), (32) для первых ![]() 6 собственных форм колебаний стержня с шагом интегрирования по времени
6 собственных форм колебаний стержня с шагом интегрирования по времени ![]() 3.10-7 с, граничными и начальными условиями вида (9), (10). После определенного числа циклов счета в системе устанавливается стационарный виброударный процесс. Вычисления прекращаются, когда мощность виброударного процесса за время ~2c изменяется не более чем на 1%. По алгоритму быстрого преобразования Фурье (БПФ) рассчитываются амплитудные спектры сигналов смещения (11) и ударной силы (28) с разрешением по частоте
3.10-7 с, граничными и начальными условиями вида (9), (10). После определенного числа циклов счета в системе устанавливается стационарный виброударный процесс. Вычисления прекращаются, когда мощность виброударного процесса за время ~2c изменяется не более чем на 1%. По алгоритму быстрого преобразования Фурье (БПФ) рассчитываются амплитудные спектры сигналов смещения (11) и ударной силы (28) с разрешением по частоте ![]() 2 Гц.
2 Гц.
По результатам расчетов динамики ВУС, полученных при значениях параметров системы ![]() (0; 1500] Н/м,
(0; 1500] Н/м, ![]() [1,3; 2] м,
[1,3; 2] м, ![]() [0; 2]мм,
[0; 2]мм, ![]() [0,01; 0,2],
[0,01; 0,2], ![]() [2,25.108; 41,5.108] Н/м2,
[2,25.108; 41,5.108] Н/м2, ![]() [0,5; 1], установлено, что не при всех комбинациях значений этих параметров можно использовать экспериментально определенные значения параметров динамической силовой характеристики обмотки. Объясняется это тем, что область их применимости ограничена деформациями основания до 200 мкм, имеющими практическое значение. Кроме того должно выполняться правило: значениям
[0,5; 1], установлено, что не при всех комбинациях значений этих параметров можно использовать экспериментально определенные значения параметров динамической силовой характеристики обмотки. Объясняется это тем, что область их применимости ограничена деформациями основания до 200 мкм, имеющими практическое значение. Кроме того должно выполняться правило: значениям ![]() ,
, ![]() должны соответствовать малые деформации основания, а значениям
должны соответствовать малые деформации основания, а значениям ![]() ,
, ![]() - большие значения деформации основания до 200 мкм.
- большие значения деформации основания до 200 мкм.
Рассмотрим результаты расчета динамики ВУС в установившихся режимах движения при деформациях основания до 200 мкм, для которых это правило выполняется.
На рис. 4 представлены расчетные зависимости, полученные при значениях параметров системы ![]() 1500 Н/м,
1500 Н/м, ![]() 1,605 м (
1,605 м (![]() 100 Гц),
100 Гц), ![]() 1. Использованы следующие обозначения: (1) – РУП,
1. Использованы следующие обозначения: (1) – РУП, ![]() 2,25.108 Н/м2,
2,25.108 Н/м2, ![]() 0,2; (2) – РУП,
0,2; (2) – РУП, ![]() 4,15.109 Н/м2,
4,15.109 Н/м2, ![]() 0,01; (3) – СУП,
0,01; (3) – СУП, ![]() 4,15.109 Н/м2,
4,15.109 Н/м2, ![]() 0,01.
0,01.
На рис. 5 представлены расчетные зависимости, полученные при значениях параметров системы ![]() 1,605 м (
1,605 м (![]() 100 Гц),
100 Гц), ![]() 384 мкм,
384 мкм, ![]() 4,15.109 Н/м2 ,
4,15.109 Н/м2 , ![]() 1. Использованы следующие обозначения: (1) – РУП,
1. Использованы следующие обозначения: (1) – РУП, ![]() 0,01; (2) – РУП,
0,01; (2) – РУП, ![]() 0,2; (3) – СУП,
0,2; (3) – СУП, ![]() 0,01; (4) – СУП,
0,01; (4) – СУП, ![]() 0,2.
0,2.
На рис. 6 представлены расчетные зависимости, полученные при значениях параметров системы ![]() 1500 Н/м,
1500 Н/м, ![]() 384 мкм,
384 мкм, ![]() 1. Использованы следующие обозначения: (1) – РУП,
1. Использованы следующие обозначения: (1) – РУП, ![]() 2,25.108 Н/м2,
2,25.108 Н/м2, ![]() 0,2; (2) – РУП,
0,2; (2) – РУП, ![]() 4,15.109 Н/м2,
4,15.109 Н/м2, ![]() 0,01; (3) – СУП,
0,01; (3) – СУП, ![]() 4,15.109 Н/м2,
4,15.109 Н/м2, ![]() 0,01.
0,01.
Анализ зависимостей на рис.4, рис.5 и рис.6, позволяет сделать следующие выводы.
- Размах виброударного процесса ограничен величиной зазора ![]() (1).
(1).
- С увеличением величины зазора ![]() интенсивность виброударного процесса сначала увеличивается, а потом уменьшается до нуля (рис.4,б,е). Максимум интенсивности приходится на величину зазора
интенсивность виброударного процесса сначала увеличивается, а потом уменьшается до нуля (рис.4,б,е). Максимум интенсивности приходится на величину зазора ![]() 384 мкм, при которой, согласно формуле (33), постоянная составляющая электродинамического усилия (2) вызывает статическую деформацию стержня
384 мкм, при которой, согласно формуле (33), постоянная составляющая электродинамического усилия (2) вызывает статическую деформацию стержня ![]() .
.
- Чем больше относительное демпфирование ![]() , тем интенсивность виброударного процесса меньше (рис. 5,а,б).
, тем интенсивность виброударного процесса меньше (рис. 5,а,б).
- С увеличением длины ![]() незакрепленного участка стержня (уменьшением первой собственной частоты
незакрепленного участка стержня (уменьшением первой собственной частоты ![]() его колебаний (рис. 3,а) интенсивность виброударного процесса увеличивается (рис. 6,б,е).
его колебаний (рис. 3,а) интенсивность виброударного процесса увеличивается (рис. 6,б,е).

Рис. 4. Зависимость расчетных параметров динамики ВУС «обмотка – сердечник» от величины зазора ![]() в срединном сечении стержня
в срединном сечении стержня

Рис. 5. Зависимость параметров сигнала ударной силы ![]() ВУС «обмотка – сердечник» от амплитуды
ВУС «обмотка – сердечник» от амплитуды ![]() знакопеременной составляющей электродинамического усилия при различных значениях относительного демпфирования
знакопеременной составляющей электродинамического усилия при различных значениях относительного демпфирования ![]()

Рис. 6. Зависимость расчетных параметров динамики ВУС «обмотка – сердечник» от низшей собственной частоты колебаний стержня ![]()
- Погонная жесткость основания ![]() оказывает существенное влияние на виброударный режим движения и параметры сигнала ударной силы. При ее минимальном значении
оказывает существенное влияние на виброударный режим движения и параметры сигнала ударной силы. При ее минимальном значении ![]() = 2,25.108 Н/м2 и большом относительном демпфировании
= 2,25.108 Н/м2 и большом относительном демпфировании ![]() 0,2 в ВУС устанавливаются периодические режимы движения типа 1Т, 2Т и т.д. При ее максимальном значении
0,2 в ВУС устанавливаются периодические режимы движения типа 1Т, 2Т и т.д. При ее максимальном значении ![]() = 4,15.109 Н/м2 и малом относительном демпфировании
= 4,15.109 Н/м2 и малом относительном демпфировании ![]() 0,01 в ВУС практически всегда реализуется стохастический виброударный режим движения, что видно по флуктуациям значений параметра
0,01 в ВУС практически всегда реализуется стохастический виброударный режим движения, что видно по флуктуациям значений параметра ![]() на рис. 4,д и рис. 6,д.
на рис. 4,д и рис. 6,д.
- Верхняя частота ![]() спектра сигнала ударной силы
спектра сигнала ударной силы ![]() лежит в интервале от 800 до 5000 Гц. Ее значение сильно зависит от погонной жесткости основания
лежит в интервале от 800 до 5000 Гц. Ее значение сильно зависит от погонной жесткости основания ![]() и слабо зависит от таких параметров ВУС, как зазор
и слабо зависит от таких параметров ВУС, как зазор ![]() , амплитуда
, амплитуда ![]() знакопеременной составляющей электродинамического усилия, длина
знакопеременной составляющей электродинамического усилия, длина ![]() незакрепленного участка стержня и относительного демпфирования
незакрепленного участка стержня и относительного демпфирования ![]() (рис. 4,в; рис. 5,в; рис. 6,в).
(рис. 4,в; рис. 5,в; рис. 6,в).
Оценим влияние структурных и физико - механических параметров ВУС на спектральный состав сигнала ударной силы. На рис. 7 представлены результаты расчетов, полученные при значениях параметров системы ![]() 1500 Н/м,
1500 Н/м, ![]() 1,605 м (
1,605 м (![]() 100 Гц),
100 Гц), ![]() 1, (а), (в), (д) -
1, (а), (в), (д) - ![]() 20 мкм, (б), (г), (е) -
20 мкм, (б), (г), (е) - ![]() 1000 мкм. Использованы следующие обозначения: (а), (б) – РУП,
1000 мкм. Использованы следующие обозначения: (а), (б) – РУП, ![]() 2,25.108 Н/м2,
2,25.108 Н/м2, ![]() 0,2; (в), (г) – РУП,
0,2; (в), (г) – РУП, ![]() 4,15.109 Н/м2,
4,15.109 Н/м2,![]() 0,01; (д), (е) – СУП,
0,01; (д), (е) – СУП, ![]() 4,15.109 Н/м2,
4,15.109 Н/м2, ![]() 0,01. Видно, что спектральный состав сигналов ударных сил в ВУС с РУП и СУП отличается большим разнообразием. Установлены следующие особенности изменения спектров сигнала ударной силы с развитием дефекта.
0,01. Видно, что спектральный состав сигналов ударных сил в ВУС с РУП и СУП отличается большим разнообразием. Установлены следующие особенности изменения спектров сигнала ударной силы с развитием дефекта.
- При малом зазоре, большом демпфировании и минимальной погонной жесткости основания спектр сигнала ударной силы в РУП имеет вид амплитудно - импульсной модуляции в зоне собственной частоты колебаний стержня на упругом основании (~700 Гц на рис. 7,а). С увеличением величины зазора значения амплитуд дискретных составляющих спектра, целочисленно кратных частоте электродинамического усилия, номинально 100Гц, увеличиваются; огибающая дискретных амплитуд спектра принимает вид одиночного косинусоидального импульса с шириной большого лепестка до 2 кГц (рис. 7,б).
- При малом зазоре, малом демпфировании и большой погонной жесткости основания спектр сигнала ударной силы в РУП представляет собой широкополосный шум, интенсивность которого уменьшается с ростом частоты (рис. 7,в). С увеличением величины зазора от 20 до 1000 мкм значения амплитуд дискретных составляющих спектра, кратных частоте вынуждающей электродинамической силы, номинально 100 Гц, увеличиваются (рис. 7,г), а интенсивность шумовой составляющей спектра остается практически неизменной. При зазоре ![]() 1,3 мм спектр становится дискретным.
1,3 мм спектр становится дискретным.
- При малом зазоре, малом демпфировании, и большой жесткости основания спектр сигнала ударной силы в СУП также как и в РУП представляет собой широкополосный шум. Однако в отличие от сигнала ударной силы в РУП его интенсивность уменьшается с ростом частоты быстрее и напоминает лепестки синусоидальных волн. Выделяются отдельные дискретные составляющие, кратные частоте вынуждающей электродинамической силы, номинально 100 Гц (рис. 7,г). С увеличением величины зазора интенсивность шумовой составляющей спектра изменяется незначительно, а амплитуды дискретных составляющих спектра увеличиваются. При зазоре ![]() 1 мм спектр сигнала ударной силы становится дискретным (рис. 7,е).
1 мм спектр сигнала ударной силы становится дискретным (рис. 7,е).
По результатам анализа можно сделать следующие выводы.
- В ВУС с РУП и СУП реализуются стохастические, почти периодические и периодические виброударные режимы движения типа 1Т, 2Т и т.д..
- При небольшом (до 1000 мкм) зазоре и амплитуде электродинамического усилия![]() 500 Н/м спектр сигнала ударной силы в ВУС с РУП и СУП даже при неизменных граничных условиях закрепления обмотки представляет собой преимущественно широкополосный шум с верхней частотой от 800 Гц до 5 кГц. Случайный характер закрепления обмотки [3] в процессе эксплуатации генератора увеличивает область параметров ВУС, при которых реализуются стохастические режимы движения.
500 Н/м спектр сигнала ударной силы в ВУС с РУП и СУП даже при неизменных граничных условиях закрепления обмотки представляет собой преимущественно широкополосный шум с верхней частотой от 800 Гц до 5 кГц. Случайный характер закрепления обмотки [3] в процессе эксплуатации генератора увеличивает область параметров ВУС, при которых реализуются стохастические режимы движения.
- Тенденция изменения расчетных параметров сигнала ударной силы с развитием дефекта зависит от изменяемого структурного параметра системы; может носить трендовый (рис.6) и экстремальный (рис.4) характер. Значения расчетных параметров сигнала ударной силы в ВУС с РУП больше чем в ВУС с СУП.
- Бифуркация режимов движения, возникающая при изменении структурных параметров системы и вынуждающей электродинамической силы, хорошо обнаруживается по скачкообразному изменению СКЗ сигнала ударной силы ![]() (рис. 4,е; рис. 5,б; рис. 6,е).
(рис. 4,е; рис. 5,б; рис. 6,е).
Расчеты показывают, при величине зазора ![]() 2 мм максимальные знакопеременные изгибные напряжения в заделке незакрепленного участка стержня длиной
2 мм максимальные знакопеременные изгибные напряжения в заделке незакрепленного участка стержня длиной ![]() не превышают 20 МПа, т.е. являются неопасными. Вместе с тем на практике имели место случаи, «когда верхний стержень обмотки был уложен в паз с зазором по отношению к нижнему стержню около 7 мм. В результате вибрации в пазовой части в стержне сломались верхние элементарные проводники и изоляция» [8]. Поэтому при значительных зазорах дефект ослабления обмотки в пазовой части следует считать опасным, влияющим на надежность работы генератора.
не превышают 20 МПа, т.е. являются неопасными. Вместе с тем на практике имели место случаи, «когда верхний стержень обмотки был уложен в паз с зазором по отношению к нижнему стержню около 7 мм. В результате вибрации в пазовой части в стержне сломались верхние элементарные проводники и изоляция» [8]. Поэтому при значительных зазорах дефект ослабления обмотки в пазовой части следует считать опасным, влияющим на надежность работы генератора.

Рис. 7. Фрагменты амплитудных спектров сигнала ударной силы в различных установившихся режимах движения ВУС «обмотка – сердечник»
Выводы
1. Построена динамическая диагностическая модель узла крепления обмотки в пазу сердечника статора, которая описывает распределенные линейные и сильно нелинейные (виброударные) радиальные изгибные колебания стержня обмотки в пазу сердечника с учетом экспериментально определенных динамических силовых характеристик ударных пар. Включает в себя 12 структурных и физико - механических параметров системы и позволяет количественно оценивать параметры ударных сил, возбуждающих виброакустические колебания конструкции статора работающего генератора.
2. Изучена динамика симметричной распределенной виброударной системы «обмотка – сердечник» в установившихся режимах движения с учетом первых 6- ти собственных форм колебаний стержня обмотки и показано, что в системе реализуются стохастические, почти периодические и периодические виброударные режимы движения типа 1Т, 2Т и т.д.
3. Установлено, что при небольшом (до 1000 мкм) зазоре между стержнями обмотки в пазовой части и амплитуде знакопеременной составляющей электродинамического усилия ![]() 500 Н/м спектр сигнала радиальной ударной силы в виброударной системе с распределенной и сосредоточенной ударной парой представляет собой преимущественно широкополосный шум с верхней частотой от 800 Гц до 5 кГц.
500 Н/м спектр сигнала радиальной ударной силы в виброударной системе с распределенной и сосредоточенной ударной парой представляет собой преимущественно широкополосный шум с верхней частотой от 800 Гц до 5 кГц.
4. Тенденция изменения СКЗ сигнала ударной силы с развитием дефекта зависит от изменяемого структурного параметра системы; может носить трендовый и экстремальный характер.
5. Бифуркация режимов движения, возникающая при изменении структурных параметров системы и вынуждающего электродинамического усилия, хорошо обнаруживается по скачкообразному изменению СКЗ сигнала ударной силы.
6. Рассчитаны спектры сигналов ударных сил, возбуждающих виброакустические колебания конструкции статора на разных стадиях развития дефекта. Они могут быть использованы для имитационного моделирования вынужденных реакций конструкции статора, проводимого с целью ответа на вопрос о возможности их спектрального обнаружения на обшивке корпуса статора работающего генератора и определения спектральных диагностических признаков дефекта ослабления крепления статорной обмотки в пазовой части формализованным методом.
Литература
1. В.А. Цветков Диагностика мощных генераторов. – М.: НЦ ЭНАС, 1995. – 235 с.
2. Проектирование турбогенераторов: учеб. пособие для вузов / В.И. Извеков, Н.А. Серихин, А.И. Абрамов. - М.: МЭИ, 2005. - 440 с.
3. Эксплуатация турбогенераторов с непосредственным охлаждением / Под. ред. Л.С. Линдорфа, Л.Г. Мамиконянца. – М.: Энергия, 1972. – 352 с.
4. Тимошенко С.П., Янг Д.Х., Уивер У. Колебания в инженерном деле / Пер. с англ. Л.Г. Корнейчука; Э.И. Григолюка. – М.: Машиностроение. - 1985. -472 с.
5. Ильин М.М., Колесников К.С., Саратов Ю.С. Теория Колебаний: Учеб. для вузов / Под. общ. ред. К.С. Колесникова. – М.: МГТУ им. Н.Э. Баумана, 2003. -272 с.
6. Бидерман В.Л. Прикладная теория механических колебаний. Учебное пособие для втузов. - М.: Высшая школа, 1972. – 416 с.
7. Справочник по ремонту турбогенераторов / Под. ред. Х.А. Бекова, В.В. Барило. - М.: ИПКгосслужбы, ВИПКэнерго, 2006. – 724 с.
8. Ростик Г.В. Оценка технического состояния турбогенератора. Учебно-практическое пособие. М.: ИПКгосслужбы, 2008. – 492 с.
Публикации с ключевыми словами: динамика, математическая модель, вибрация, дефект, спектр, турбогенератор, обмотка, сердечник, узел крепления, диагностическая модель, структурный параметр, виброударная система, ударная пара, режим движения, ударная сила
Публикации со словами: динамика, математическая модель, вибрация, дефект, спектр, турбогенератор, обмотка, сердечник, узел крепления, диагностическая модель, структурный параметр, виброударная система, ударная пара, режим движения, ударная сила
Смотри также:
- Методология моделирования трехмерных механических систем с помощью универсальных программных комплексов анализа
- Математические модели балки и направляющих на ее основе для программ моделирования
- Сравнение результатов анализа динамических систем на макроуровне с помощью отечественных и зарубежных комплексов САПР
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



