научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 08, август 2013
DOI: 10.7463/0813.0578962
УДК 621.7.043.
Россия, МГТУ им. Н.Э. Баумана
Введение
При строительстве трубопроводов применяются такие соединительные детали трубопроводов, как переходники рис. 1. Стальные переходники используются для соединения труб с разным диаметром. Благодаря переходникам трубопровод становится надёжным и прочным.

Рис.1. Типы трубных переходников: а) концентрический симметричный; б) крутоизогнутый; в) асимметричный; г) конфузорно-диффузорный; д) ступенчатый.
При изготовлении переходников используют методы обработки резанием. Коэффициент использования материала при обработке резанием деталей переходников низкий, что является серьезным недостатком. С целью повышения коэффициента использования материала, заготовку для механической обработки получают штамповкой.
В работах [1–8] рассмотрено несколько вариантов изготовления переходников из трубчатых заготовок. Наиболее экономичным среди различных вариантов изготовления переходников методами листовой штамповки, является метод получения переходников совмещением раздачи и обжима. Совмещение операций раздачи и обжима позволяет интенсифицировать процесс формоизменения трубчатой заготовки и получить ступенчатые и конические детали с любым углом конусности за один переход с минимальными отходами металла [2-4].
Особенностью совмещенного процесса обжима-раздачи является наличие двух участков пластической деформации, разделённых между собой упругодеформируемым участком заготовки. На одном из участков пластической деформации осуществляется увеличение диаметра заготовки, т.е. раздача, на другом - уменьшение диаметра заготовки, т.е. обжим.
В работе [6] показано, что при одинаковых условиях на обоих участках деформирование на участке раздачи осуществляется более интенсивно, чем на участке обжима.
Целью работы является исследование и расчет влияния величины коэффициента трения на напряженное и деформированное состояние заготовки при совмещении операций раздачи и обжима при изготовлении переходников, а также определение изменения высоты и толщины стенки заготовки при совмещенной операции.
В работе проведено исследование совмещенного процесса раздачи и обжима, которое позволило определить действующие напряжения и деформаций для обеих зон раздачи и обжима заготовки. Научная новизна работы заключается в построении математических моделей для управления процессом одновременного деформирования заготовка посредством совмещения операций обжима и раздачи заготовки при варьировании величиной коэффициента трения между заготовкой и инструментом.
Методы исследования
При анализе напряжённого и деформированного состояний совмещённой операции обжима и раздачииспользуется метод суперпозиции, при котором общий очаг пластической деформации условно разбивается на две области раздачи и обжима,решение проводится для каждой из областей при определённых, соответствующих данной области, граничных условиях. Затем полученные решения распространяются на весь общий очаг деформации.
При совпадении очагов деформации обжима и раздачи, в которых действуют окружные, соответственно сжимающие и растягивающие напряжения, граница очагов деформации проходит в сечении, где меридиональные сжимающие напряжения при обжиме и раздаче равны между собой. Напряженное и деформированное состояние заготовки в этом случае определяют на основании ранее полученных зависимостей для обжима и раздачи. Сила деформирования заготовки в этих условиях для обжима и раздачи, очевидно, одинакова. Наибольшее изменение диаметра исходной заготовки можно получить при назначении наибольших коэффициентов обжима и раздачи заготовки. Общий коэффициент совмещенной операции обжим с раздачей равен
![]() ,
,
где ![]() – коэффициент обжима заготовки;
– коэффициент обжима заготовки; ![]() – коэффициент раздачи заготовки;
– коэффициент раздачи заготовки; ![]() –радиус исходной заготовки;
–радиус исходной заготовки; ![]() –максимальный радиус заготовки после операции раздачи;
–максимальный радиус заготовки после операции раздачи; ![]() –минимальный радиус заготовки после операции обжима.
–минимальный радиус заготовки после операции обжима.
При допустимых значениях коэффициентов обжима![]() и раздачи
и раздачи![]() , общий коэффициент совмещенной операции будет равен
, общий коэффициент совмещенной операции будет равен ![]() [4].
[4].
Метод суперпозиции даёт наглядное представление о процессе формоизменения, однако целостную, физическую картину механизма деформирования, он, к сожалению, отразить не в состоянии. Тем не менее, его использование для отдельных операций даёт возможность избежать трудностей при анализе процессов формоизменения. В соответствии с представленным рис. 2, область обжима распространяется от радиуса ![]() до
до ![]() , область раздачи от
, область раздачи от ![]() до
до ![]() .
.

Рис. 2. Схема напряженного и деформированного состояний заготовки при совмещенной операции обжима и раздачи
Определение напряжений и деформаций в очаге деформации
Для определения полей напряжений по очагу деформации заготовки при раздаче и обжиме применяют метод совместного решения приближенного дифференциального уравнения равновесия и уравнения пластичности. Принятые допущения: схема напряженного состояния- плоская (![]() ). Общее дифференциальное уравнение равновесия для тонкостенной оболочки имеет вид
). Общее дифференциальное уравнение равновесия для тонкостенной оболочки имеет вид
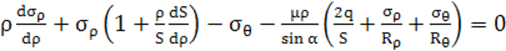 . (1)
. (1)
Здесь ![]() — главные нормальнее напряжения в меридиональном направлении;
— главные нормальнее напряжения в меридиональном направлении; ![]() — главные нормальнее напряжения в тангенциальном направлении;
— главные нормальнее напряжения в тангенциальном направлении; ![]() — толщина стенки деформируемой заготовки;
— толщина стенки деформируемой заготовки; ![]() — коэффициент трения между инструментом и заготовкой;
— коэффициент трения между инструментом и заготовкой; ![]() — радиус кривизны оболочки в меридиональном сечении;
— радиус кривизны оболочки в меридиональном сечении; ![]() — радиус кривизны оболочки в тангенциальном сечении.
— радиус кривизны оболочки в тангенциальном сечении.
Условие пластичности для операции обжима, имеет вид
![]() , (2)
, (2)
условие пластичности для операции раздача - вид
![]() . (3)
. (3)
Здесь ![]() — напряжение текучести материала.
— напряжение текучести материала.
Изменение толщины стенки по очагу деформации определяем по следующим зависимостям:
- для области операции обжима
 , (4)
, (4)
- для области операции раздачи
 . (5)
. (5)
Здесь ![]() — исходная толщина заготовки;
— исходная толщина заготовки; ![]() — исходный радиус заготовки;
— исходный радиус заготовки;![]() –текущий радиус в области операции обжима;
–текущий радиус в области операции обжима;![]() – текущий радиус в области операции раздачи.
– текущий радиус в области операции раздачи.
Расчеты проведены на ЭВМ с использованием программы MathCAD. Исходными данными являлись значения радиусоврасчетных точек:![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;![]() .
. ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() – угол конуса детали переходника.
– угол конуса детали переходника.
Варьировали значения следующих параметров:
- значения коэффициента трения  на трех уровнях
на трех уровнях ![]() ;
;
- значения текущего радиуса обжима  на пяти уровнях
на пяти уровнях ![]() ;
;
- значения текущего радиуса раздачи  на пяти уровнях
на пяти уровнях ![]() .
.
Исходной заготовкой является стакан, полученный многопереходной вытяжкой из круглой плоской заготовки без межоперационных отжигов.
Упрочнение при этом учитывали по зависимости
![]() ,
,
где ![]() — напряжение текучести n-го перехода;
— напряжение текучести n-го перехода; ![]() — коэффициент вытяжки n-го перехода.
— коэффициент вытяжки n-го перехода.
Эта формула учитывает предыдущую наследственность упрочнения следующим образом:
- для области операции обжима
![]() ,
, ![]() ;
;
- для области операции раздачи
![]() ,
, ![]() .
.
Решая совместно уравнения (1) и (2) с учетом изменения толщины стенки в очаге деформации по зависимости (4) для обжима, и (1), (3), (5) - для раздачи, получаем выражения, характеризующее распределение напряжений в очаге деформации в меридиональном направлении:
- для области операции обжима
![]() , (6)
, (6)
![]() ; (7)
; (7)
- для области операции раздачи
 , (8)
, (8)
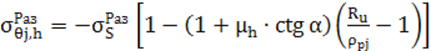 . (9)
. (9)
Результаты расчета представлены на рис. 3. Из графиков видно, что с увеличением коэффициента трения увеличиваются сжимающие напряжения ![]() и уменьшаются растягивающие напряжения
и уменьшаются растягивающие напряжения ![]() .
.
|
а) |
|
б) |
|
в) |
Рис. 3. Напряжения |
Определение максимальных напряжений и сил деформирования
Определим величину максимальногомеридионального сжимающего напряжения с учетом изгиба и спрямления на входе в очаг деформации,при коэффициенте трения ![]() =0,15для операции обжима:
=0,15для операции обжима:
 , (10)
, (10)
![]() Мпа.
Мпа.
Сила деформирования при операции обжиме равна
![]() ,
,
![]() ,
, ![]() .
.
Определим величину максимального меридионального сжимающего напряжения с учетом изгиба и спрямления на входе в очаг деформации, при коэффициенте трения ![]() =0,15, для операции раздачи:
=0,15, для операции раздачи:
 , (11)
, (11)
![]() МПа
МПа
Сила деформирования при операции раздачи равна
![]() ,
,
![]() ,
, ![]() .
.
Погрешность значений сил деформирования для операции обжима и раздачи составила
![]() .
.
Получили, что при одинаковых коэффициенте трения, степени деформации и углах конусности пуансона и матрицы сила раздачи примерно на 75% меньше силы обжима, в связи с чем раздача происходит более интенсивно, чем обжим. Поэтому сила раздачи будет недостаточна для получения конической части обжимом. Увеличить коэффициент формоизменение при обжиме можно, варьируя коэффициентом трения. Для получения более интенсивного обжима, очевидно, необходимо назначить коэффициент трения для обжима меньше, чем для раздачи. Из анализа напряженного состояния можно заметить, что максимальные сжимающие напряжения в меридиональном направлении при раздаче меньше, чем при обжиме. Поэтому необходимо увеличивать величину ![]() для раздачи. Увеличение напряжения можно добиться, если назначить коэффициент трения при раздаче больше, чем при обжиме, а также применить дополнительный подпор в меридиональном направлении.
для раздачи. Увеличение напряжения можно добиться, если назначить коэффициент трения при раздаче больше, чем при обжиме, а также применить дополнительный подпор в меридиональном направлении.
Влияние коэффициента трения на напряжения
Проведем варьирование значением коэффициента трения между инструментом и заготовкой при операциях раздаче и при обжиме и вычислим значения максимальных меридиональных напряжений в зависимости от коэффициента трения.
Значения коэффициента трения при операции обжима равно  ,
,
значения коэффициента трения при операции раздачи — 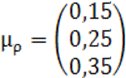 .
.
Подставляем значения ![]() в уравнение (10), получим значение максимального сжимающего меридионального напряжения при различных значениях
в уравнение (10), получим значение максимального сжимающего меридионального напряжения при различных значениях ![]() для обжима
для обжима
 .
.
Подставляем значения ![]() в уравнение (11), получим значение максимального сжимающего меридионального напряжения при различных значениях
в уравнение (11), получим значение максимального сжимающего меридионального напряжения при различных значениях ![]() для раздачи
для раздачи
 .
.
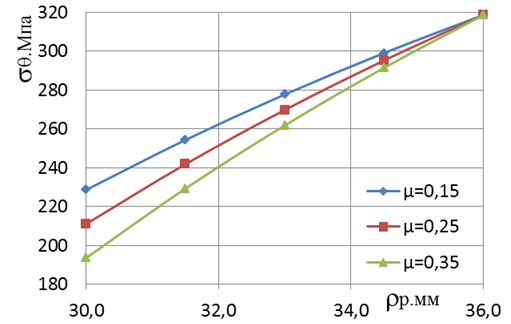
Результаты расчета представлены на рис. 4, при различных значениях ![]() для обжима и
для обжима и ![]() для раздачи.
для раздачи.
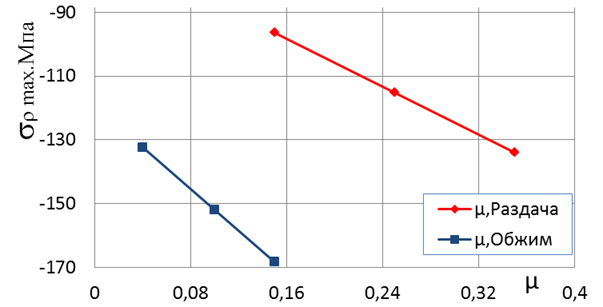
Рис. 3. Зависимость ![]() от
от ![]()
Анализируя полученные решения, можно отметить, что при одинаковых коэффициентах трения и при прочих равных условиях максимальные сжимающие напряжения в меридиональном направлении при раздаче меньше, чем при обжиме. Равномерно изменяя значения коэффициента трения (увеличивая при раздаче и уменьшая при обжиме), добиваемся повышения максимальных напряжений при раздаче, тем самым повышая интенсивность протекания процесса обжима. Оптимальными являются значения коэффициентов трения 0,04 при обжиме и 0,35 при раздаче. Максимальные напряжения при раздаче получаются чуть больше, чем при обжиме. Этого достаточно для равномерного протекания одновременно раздачи и обжима.
Определение деформаций
Для нахождения деформаций используем уравнение связи между напряжениями и деформациями [5]
![]() . (12)
. (12)
Условие несжимаемости имеет вид
![]() . (13)
. (13)
Здесь ![]() ,
, ![]() и
и ![]() - напряжения, действующие соответственно в меридиональном и широтном направлениях, а также перпендикулярно срединной поверхности заготовки;
- напряжения, действующие соответственно в меридиональном и широтном направлениях, а также перпендикулярно срединной поверхности заготовки; ![]() ,
, ![]() и
и ![]() - приращение деформаций в тех же направлениях.
- приращение деформаций в тех же направлениях.
Приращение деформаций определяем по формулам
![]() , (14)
, (14)
![]() , (15)
, (15)
![]() . (16)
. (16)
Для плоско-напряженного состояния ![]() , поэтому справедливо равенство
, поэтому справедливо равенство
![]() . (17)
. (17)
Подставляя значения ![]() из формул (14, 15, 16) в формулу (17) и произведя несложные преобразования, получим
из формул (14, 15, 16) в формулу (17) и произведя несложные преобразования, получим
![]() . (18)
. (18)
Обозначим ![]() , где
, где ![]() – текущий коэффициент соотношения полей напряжений.
– текущий коэффициент соотношения полей напряжений.
Интегрируя уравнение (18), получим
![]() . (19)
. (19)
Считаем, что ![]() - является осредненной постоянной величиной по очагу деформации, поэтому при интегрировании ее можно вынести за знак интеграла. В последующих расчетах
- является осредненной постоянной величиной по очагу деформации, поэтому при интегрировании ее можно вынести за знак интеграла. В последующих расчетах ![]() принимается переменной величиной, зависящей от
принимается переменной величиной, зависящей от ![]() и
и ![]() . Это допущение отражено в работе Е.А. Попова [5].
. Это допущение отражено в работе Е.А. Попова [5].
Область обжима
Произвольная постоянная интегрирования определяется из граничных условий рис. 2, при ![]() ,
, ![]() .
.
Подставляя граничные условия в формулу (19), получаем ![]() .
.
Тогда ![]() .
.
Откуда получаем следующие значения:
- деформация по толщине
![]() ; (20)
; (20)
- окружную деформацию определяем по формуле
![]() . (21)
. (21)
Меридиональную деформацию устанавливаем из условия несжимаемости при известных ![]() и
и ![]() :
:
![]() . (22)
. (22)
Толщину стенки в очаге деформации получаем из формулы (20):
 . (23)
. (23)
Используя формулы (6), (7), (20) – (23) при коэффициенте трения ![]() , определяем напряжения
, определяем напряжения![]() , деформации e и толщину Sобжимаемой части заготовки в любом точке с текущем радиусом
, деформации e и толщину Sобжимаемой части заготовки в любом точке с текущем радиусом ![]() , который изменяется от
, который изменяется от ![]() до
до ![]() .
.
Результаты расчета напряжения ![]() представлены на рис. 5, при различных значениях
представлены на рис. 5, при различных значениях ![]() для обжима.
для обжима.

Рис. 5. Зависимость![]() от
от![]()
Результаты расчета деформацииe представлены на рис. 6, при различных значениях ![]() для обжима.
для обжима.
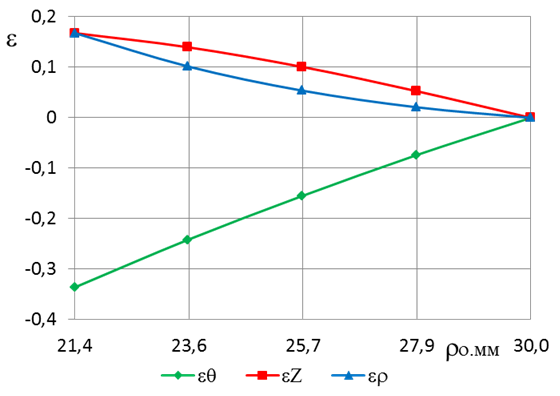
Рис. 6. Изменение деформации (окружной ![]() , по толщине
, по толщине ![]() , меридиональной деформации
, меридиональной деформации ![]() ) относительно от расстояния от центра заготовки
) относительно от расстояния от центра заготовки
Результаты расчета изменения толщины S заготовки представлены на рис. 7, при различных значениях ![]() для обжима.
для обжима.

Рис. 7. Изменение толщины стенки заготовки относительно расстоянияот центра заготовки
Из приведенных выше расчетов можно заметить, что деформированное состояние при обжиме неоднородно по очагу деформации, оно меняется в зависимости от соотношения нормальных напряжений ![]() и
и ![]() . Когда меридиональная деформация заготовки в процессе деформирования равна нулю (
. Когда меридиональная деформация заготовки в процессе деформирования равна нулю (![]() ), при этом, меридиональные напряжения равны
), при этом, меридиональные напряжения равны ![]() , а абсолютные значения напряжений
, а абсолютные значения напряжений ![]() и
и ![]() , то деформированное состояние в этих точках является плоским. На остальных участках заготовки деформированное состояние объемное. Когда меридиональные напряжения
, то деформированное состояние в этих точках является плоским. На остальных участках заготовки деформированное состояние объемное. Когда меридиональные напряжения ![]() уменьшаются происходит утолщение стенки (
уменьшаются происходит утолщение стенки (![]() ).
).
Область раздачи
Произвольная постоянная интегрирования в формуле (43) для области раздачи определяется из граничных условий. При ![]() , толщина стенки S будет равна соответствующей толщине стенки исходной заготовки (граничные условия при раздаче и граничные условия при обжиме одинаковые при
, толщина стенки S будет равна соответствующей толщине стенки исходной заготовки (граничные условия при раздаче и граничные условия при обжиме одинаковые при ![]() ) (рис. 2).
) (рис. 2).
Подставляем граничные условия в формулу (19), получаем
![]() .
.
Тогда
![]() .
.
Откуда получим формулы текущей деформации ![]() и толщины
и толщины ![]() в области вытяжки в любой точке с радиусом
в области вытяжки в любой точке с радиусом ![]() .
.
Деформация по толщине определяем по формуле
 , (24)
, (24)
окружную деформацию — по формуле
![]() . (25)
. (25)
Меридиональную деформацию устанавливаем из условия несжимаемости при известных![]() и
и ![]() :
:
![]() . (26)
. (26)
Толщину стенки в очаге деформации можно получить из формулы (24):
 . (27)
. (27)
Используя формулы (8), (9), (24) – (27) при коэффициенте трения ![]() определяем напряжения
определяем напряжения ![]() и
и ![]() , деформации e и толщину Sраздаваемой части заготовки в любом точке с текущем радиусом
, деформации e и толщину Sраздаваемой части заготовки в любом точке с текущем радиусом ![]() , который изменяется от
, который изменяется от ![]() до
до ![]() .
.
Результаты расчета напряжения представлены на рис. 8, при различных значениях![]() для раздачи.
для раздачи.

Рис. 8. Зависимость ![]() и
и ![]() от
от![]()
Результаты расчета деформацииe представлены на рис. 9, при различных значениях ![]() для раздачи.
для раздачи.

Рис. 9. Изменение деформации (окружной ![]() , по толщине
, по толщине![]() , меридиональной деформации
, меридиональной деформации![]() ) относительно от расстояния от центра заготовки
) относительно от расстояния от центра заготовки
Результаты расчета изменения толщины Sзаготовки представлены на рис. 10, при различных значениях ![]() для раздачи.
для раздачи.
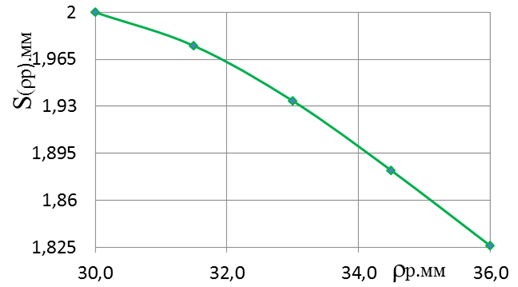
Рис. 10. Изменение толщины стенки заготовки относительно расстоянияот центра заготовки
Из приведенных выше расчетов можно заметить, что деформированное состояние при раздаче также неоднородно по очагу деформации. Оно меняется в зависимости от соотношения нормальных напряжений ![]() и
и ![]() ,и в точках, где абсолютные значения напряжений
,и в точках, где абсолютные значения напряжений![]() и
и ![]() равны между собой, толщина заготовки в процессе деформирования не изменяется , деформированное состояние - плоское.
равны между собой, толщина заготовки в процессе деформирования не изменяется , деформированное состояние - плоское.
В общем случае деформированное состояние заготовки объемное, причем там, где ![]() , происходит утолщение стенки(
, происходит утолщение стенки(![]() ), а на участке, где
), а на участке, где![]() - утонение (
- утонение (![]() ).
).
Результаты расчетов
При обжиме толщина стенки заготовки возрастает на 18%, а при раздаче уменьшается на 9%. Так как при раздаче высота заготовки уменьшается на 9,1%, а при обжиме высота увеличивается на 16,8%, общее увеличение высоты заготовки в совмещенной операции составит 7,7%, что говорит о том, что в этой совмещенной операции превалирует все же операция обжима.
Выводы
1) Варьируя величиной коэффициента трения между заготовкой и инструментом, можно управлять процессом одновременного деформирования заготовка посредством совмещения операций обжима и раздачи.
2) Величина коэффициента трения в области раздачи деформируемой заготовки должна в (3…5 раз) превышать значения коэффициента трения в области обжима. Тем самым возрастают меридиональные сжимающие напряжения раздачи, равные или несколько больше напряжений обжима (![]() ), что обеспечивает одновременное выполнение операций раздачи и обжима.
), что обеспечивает одновременное выполнение операций раздачи и обжима.
3) Высота заготовки после деформирования увеличивается на 7,7% за счет обжима, положительное значение ![]() при обжиме компенсируется отрицательной меридиональной деформаций при раздаче.
при обжиме компенсируется отрицательной меридиональной деформаций при раздаче.
Список литературы
1. Романовский В.И. Справочник по холодной штамповке. 6-е изд., перераб. и доп. Л.: Машиностроение, Ленингр. отделение, 1979. 520 с.
2. Ковка и штамповка: справочник. В 4 т. Т. 4. Листовая штамповка / Под ред. С.С. Яковлева. М.: Машиностроение, 2010. 732 с.
3. Семёнов Е.И. Ковка и штамповка. М.: Машиностроение, 1987. 544 с.
4. Попов Е.А., Ковалев В.Г., Шубин И.Н. Технология и автоматизация листовой штамповки. М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. 480 с.
5. Попов Е.А. Основы теории листовой штамповки. М.: Машиностроение, 1977. 278 с.
6. Горбунов М.Н. Штамповка деталей из трубчатых заготовок. М.: Машгиз, 1960. 190 с.
7. Евсюков С.А. Способ получения переходников с наружным цилиндрическим пояском: пат. 2087234 Российская Федерация. 1997.
8. Евсюков С.А. Способ получения переходников с внутренним цилиндрическим пояском: пат. 2060086 Российская Федерация. 1996.
Публикации с ключевыми словами: пластичность, раздача,, обжим, переходник, совмещенная операция, уравнения равновесия, уравнения связи, напряжений и деформаций, влияние трения
Публикации со словами: пластичность, раздача,, обжим, переходник, совмещенная операция, уравнения равновесия, уравнения связи, напряжений и деформаций, влияние трения
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||