научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 09, сентябрь 2011
УДК 621.983.7
МГТУ им. Н.Э. Баумана
Одной из задач, решением которых традиционно занимаются теория и практика обработки металлов давлением, является увеличение степени деформации, достижимой за один переход при минимальных затратах. Возможности формоизменения при обжиме цилиндрических заготовок ограничиваются потерей устойчивости с образованием продольных или поперечных складок. Исследованные ранее методы силовой и термической интенсификации позволяют значительно повысить степень деформации, но их использование ограничено размерами заготовки и параметрами технологического процесса. Предложенный способ обжима позволяет повысить степень формоизменения заготовки благодаря использованию матрицы с кольцевыми канавками. Применение такого способа не требует использования нагревательного оборудования и сложных конструкций штамповой оснастки.
В качестве основных теоретических предпосылок анализа используются положения, сформулированные Е. А. Поповым в работе [1]. В начальный период образования контактного участка очага пластической деформации, особенно при наличии больших углов конусности матрицы, краевая часть заготовки отходит от поверхности матрицы. Это объясняется тем, что элементы заготовки, деформированные при перемещении из участка свободного изгиба в участок, контактирующий с матрицей, имеют определенную кривизну срединной поверхности в меридиональном сечении. Для изменения кривизны необходимо действие изгибающего момента. Так как на краевую часть заготовки не действуют внешние силы, способные вызвать изгибающий момент, необходимый для спрямления, изменение кривизны происходит за счет внутренних сил, вызванных окружными напряжениями σθ где θ –полярный угол в цилиндрических координатах.
При использовании матрицы с кольцевыми канавками кромка обжимаемой трубной заготовки в процессе формоизменения совершает движения вовнутрь канавки, а затем наружу, находясь вне контакта с поверхностью матрицы. Такая форма рабочей поверхности матрицы наилучшим образом учитывает естественную, происходящую под действием внутренних напряжений деформацию кромки заготовки и уменьшает поверхность контакта заготовки с матрицей. В результате сила контактного трения между заготовкой и матрицей эффективно снижается в том месте, которое является наиболее напряженным из-за особенностей деформации кромки заготовки.
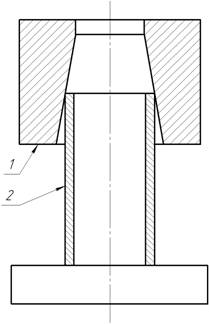
Очаг пластической деформации для обжима в матрице с кольцевыми канавками разобьем на несколько зон (рис. 1). Участки 1 имеют контакт с матрицей по вершинам выступов между канавками. На этих участках, наряду с тангенциальными напряжениями σρ, где ρ – полярный радиус в цилиндрических координатах, и окружными напряжениями σθ, на поверхности заготовки действуют нормальные контактные напряжения σn. Протяженность каждого из рассматриваемых участков можно считать равной длине усеченной вершины выступа между кольцевыми канавками. Участок 2 образуется в результате действия спрямляющего момента и не имеет контакта с рабочей поверхностью инструмента. Пластическая деформация этого участка происходит за счет сил, действующих внутри обжимаемой заготовки. Участок 3 свободного изгиба находится на входе заготовки в формообразующую часть матрицы. Заготовка на данном участке не соприкасается с инструментом. На участке 4 действует момент спрямления стенки заготовки, под влиянием которого она принимает коническую форму. На этом участке заготовки нет контакта с инструментом.

а) б)
Рис. 1. Схемы обжима заготовки: а) в гладкой матрице: 1 –матрица; 2 – заготовка;
б) схема внутренних и внешних сил при обжиме в матрице с кольцевыми канавками и зоны в очагах пластической деформации: 1 – зона контакта с инструментом; 2 – зона изгиба-спрямления концевой части заготовки; 3 – зона без контакта с инструментом; 4 – зона изгиба-спрямления на входе в матрицу; μ – коэффициент трения; r0 – радиус обжатого торца заготовки; r1, r2 … r6 – промежуточные радиусы на матрице; α – угол обжима; – высота участка контакта заготовки с матрицей; l – шаг между канавками; σρ.max – максимальные тангенциальные напряжения; Rз – радиус исходной заготовки; S – толщина стенки заготовки
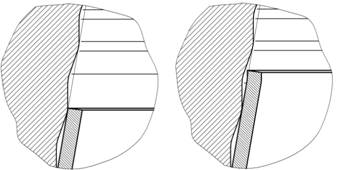
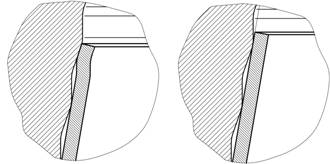
На рис. 2 показаны этапы обжима в конической матрице. На начальном этапе обжима заготовка касается вершины ступеньки (рис. 2, а). При дальнейшем деформировании концевая часть заготовки отходит от матрицы (рис. 2, б), это соответствует приведенным ниже формулам. Когда часть заготовки, не имеющая контакта с матрицей, достигает длины l (см. рис. 1), заготовка касается следующего выступа матрицы, где при контакте с матрицей заготовка обжимается (рис. 2, в). После того как заготовка прошла дальше и оказалась уже не на вершине выступа, за счет возникновения спрямляющего момента часть заготовки, находящаяся между ступеньками, спрямляется (рис. 2, г). Таким образом, по пути пластического деформирования заготовка только концевой частью деформируется в контакте со ступенчатой поверхностью матрицы. Остальная поверхность заготовки контактирует только с вершинами кольцевых выступов на поверхности матрицы.
а) б)
в) г)
Рис. 2. Этапы деформирования в ступенчатой матрице: а – выход концевой части на вершину ступеньки; б – деформирование концевого участка без контакта с инструментом; в – деформирование коническим участком ступеньки; г – спрямление участков заготовки между ступеньками
Определим σρ.max, действующее в недеформируемых стенках заготовки, в соответствии с предложенной схемой (см. рис. 1). Уравнение равновесия для случая осесимметричного деформирования тонкостенной заготовки имеет вид [1]:
ρ(dσρ/dρ) + σρ – σθ – μρ/sin α(σρ/Rρ + σθ/Rθ) = 0, (1)
где μ – коэффициент трения; α – угол наклона касательной к вершинам матрицы; Rρ – радиус кривизны заготовки в тангенциальном направлении; Rθ – радиус кривизны заготовки в окружном направлении.
Рассмотрим уравнение равновесия для каждого из участков, используя схему на рис. 1. Принимаем допущение, что зона контакта на участке 1 прямолинейна, с углом наклона α и равна величине h =1/3l. Тогда, при Rρ = ∞; Rθ = ρ/cosα; α = const, получим уравнение равновесия без учета изменения толщины:
ρ(dσρ/dρ) + σρ – σθ(1 + μctg α) = 0. (2)
После совместного решения уравнения (2) с условием пластичности Сен-Венана и отыскания произвольной постоянной из граничного условия σρ = 0 при ρ = r0 получим:
σρ = – σs(1 + μctg α) (1 – r0/ρ), (3)
где σs – напряжение текучести.
Считаем, что изгиб и спрямление с одинаковыми пределами изменения радиусов кривизны дают одинаковое увеличение меридионального напряжения на Δσρ. Величина Δσρ на участке 1 определяется по формуле из [1]
Δσρ1 = σsS/(4Rρ); (4)
Rρ = σsS/[4σρ1,2 (1 – cos α)]. (5)
где S – толщина стенки заготовки.
При подстановке значения ρ, равного r1, определим значение σρ1,2, действующее в коническом участке на границе участка 1 с участком 2 по формуле:
σρ1,2 = – σs(1 + μctg α)(1 – r0/r1). (6)
Совместным решением уравнения пластичности и уравнения равновесия (1) при условии, что µ = 0 для участка изгиба-спрямления 2, получим дифференциальное уравнение
dσρ/(σρ + σs) = –(dρ/ρ). (7)
Интегрируя (7), получаем выражение
σρ = σs + С1/ρ. (8)
Найдем величину С1 из условия, что σρ = σρ1,2 + Δσρ при ρ = r1:
С1 = σs [1 – (1 + μctg α)(1 – r0/r1) – S/(4Rρ)]; (9)
r1 = Rз – 3lsin α, (10)
Найденное значение постоянной (9) подставляем в уравнение (8) и находим уравнение для определения напряжения σρ2 в участке II при ρ = r2:
σρ2 = –σs [1 – r1/r2 + (1 + μctg α)(1 – r0/r1) – S/(4Rρ)]; (11)
r2 = Rз – (2l + h)sin α. (12)
где Rз – радиус исходной заготовки.
Решая совместно выражения (3) при ρ = r3 и (11) получаем уравнение для определения напряжения σρ1–3 на границе участков 1 и 3:
σρ1–3 = –σs [1 – r1/r2 + (1 + μctg α)(2 – r0/r1 – r2/r3) – s/(4Rρ)]; (13)
r2 = Rз – 2lsin α. (14)
На участке 3 стенка заготовки имеет коническую форму на протяжении всего процесса. Расчет напряжений σρ на этом участке проводим по формуле (3) учитывая, что µ = 0. Выражение для Δσρ на этом участке:
Δσρ3 = –σs(1 – r3/r4); (15)
r4 = Rз – (l + h) sin α, (16)
Получаем выражение для σρ на участке 3:
σρ3 = –σs [2 – r1/r2 – r3/r4 + (1 + μctg α)(2 – r0/r1 – r2/r3) + S/(4Rρ)]. (17)
Аналогичный подход используем для определения σρ.max на всех участках очага на всем протяжении очага пластической деформации до участка 4. Получаем значение напряжения σρ3,4 для границы контакта участка 3 и 4:
 (18)
(18)
где n – количество кольцевых канавок.
Учитывая влияние изгиба-спрямления при входе в матрицу получаем σρ.max, действующее в цилиндрической недеформированной стенке заготовки:
 (19)
(19)
Rρ′ = (σsS)/[4σρ.max3,4(1 – cos α)], (20)
где Rρ′ – радиус изгиба на участке изгиба-спрямления при входе в матрицу. С учетом упрочнения и изменения толщины заготовки получаем:
 (21)
(21)
По представленным формулам построены графики зависимости силы обжима от коэффициента обжима для гладкой матрицы и матрицы с тремя кольцевыми канавками (рис. 3). Расчет проведен при относительной толщине заготовки S/(2Rз) = 0,1. Шаг кольцевых канавок l рассчитан по формуле
 (22)
(22)
l = √Sr0/(2cos α). (23)
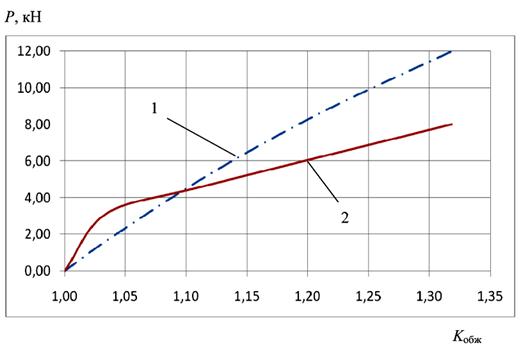
Рис. 3. График зависимости силы обжима P от коэффициента обжима Kобж: – для гладкой матрицы; 2 – для матрицы с тремя кольцевыми канавками
Графики показывают, что использование матрицы с кольцевыми канавками рационально при коэффициенте обжима Kобж > 1,1, что позволяет значительно снизить силу пластического деформирования при обжиме. Если принять в качестве условия то, что потеря устойчивости произойдет при силе P = 8 кН, то коэффициенты обжима для гладкой матрицы и матрицы с тремя кольцевыми канавками составят 1,19 и 1,32 соответственно. В этом случае увеличение Kобж составляет 11 %.
Способ обжима в матрице с кольцевыми канавками позволяет снизить силу при обжиме и повысить степень формоизменения за счет снижения влияния сил контактного трения, и тем самым уменьшить количество технологических переходов при штамповке.
Литература
1. Попов Е. А. Основы теории листовой штамповки. М.: Машиностроение, 1977. 278 с.
2. Попов О. В. Основы методики теоретического анализа при штамповке деталей из труб с применением термической и силовой интенсификации // Кузнечно-штамповочное производство. 1971. ╧ 6. С. 14–17.
Публикации с ключевыми словами: труба, штамповка, сила, интенсификация, кольцевые канавки, профилированная матрица, обжим
Публикации со словами: труба, штамповка, сила, интенсификация, кольцевые канавки, профилированная матрица, обжим
Смотри также:
- Разработка оптимальной технологии штамповки детали ╚подвеска╩ с использованием системы моделирования QFORM
- Моделирование процесса штамповки диска из жаропрочного никелевого сплава ЭП 742-ИД
- Моделирование процесса обратного выдавливания деталей из сплаваБрБ2 по схеме подвижного контейнера с применением DEFORM-2D
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



