научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 02, февраль 2009
УДК 621.396.677
МГТУ им. Н.Э.Баумана,
chernshv@bmstu.ru
Найденное в [1] приближенное выражение, связывающее коэффициент отражения плавной нерегулярной линии передачи (НЛП) с Т-волнами ![]() с функцией преобразования
с функцией преобразования ![]() , имеющее вид
, имеющее вид
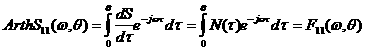 , (1)
, (1)
полезно и при решении задач частотного синтеза НЛП на отражение. Так, задаваясь отсчётами S11(ωm, θ), получаем возможность сразу же пересчитать отсчёты F11(ωm, θ), что позволяет найти хорошее начальное приближение для синтеза.
Рассмотрим методику синтеза в данном случае.
Интерполяционная формула для функции преобразования имеет вид [2]:
![]()
В свою очередь функция местных отражений может быть представлена в виде [2]:
![]()
где ![]() .
.
Волновое сопротивление НЛП при синтезе определяется, как
 ,
,
где ρ0 – волновое сопротивление начала НЛП.
Далее в зависимости от типа НЛП (коаксиальная линия, полосковая или др.) определяют её геометрические характеристики, что и является по сути целью синтеза.
Тем не менее, полученное начальное приближение конфигурация НЛП, не является окончательным, а её характеристики могут отличаться от заданных. Это приводит к тому, что, как правило, в рамках численного решения задачи синтеза требуется корректировка полученной конфигурации. В этом заключается специфика методки синтеза, основанного на начальном приближении (1).
Критерием оптимизации при таком синтезе является минимизация среднеквадратической невязки, которая записывается, как
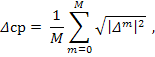
где ![]() - невязка на отдельных отсчетных частотах.,
- невязка на отдельных отсчетных частотах., ![]() – значения отсчётов коэффициента отражения, полученные при начальном приближении,
– значения отсчётов коэффициента отражения, полученные при начальном приближении, ![]() – отсчёты, заданные при синтезе.
– отсчёты, заданные при синтезе.
Критерием выхода из итерационной процедуры является попадание среднеквадратической невязки в заданную область точности: Δср ≤ ε.
В случае же невыполнения этого условия , то есть Δср ≥ ε, применяется итеративная (циклическая) корректировка.
Корректировка заключается в модификации отсчётных значений F11(ωm, θ) и повторении процедур определения конфигурации НЛП, её анализе, подсчёте невязок с последующей проверкой выполнения вышеописанных условий. Модификация F11 (ωm,θ) производится путём разложения зависимости F11m(S11m) в ряд Тейлора в окрестности ![]() до второго члена. Выражение модификации на каждой итерации имеет вид :
до второго члена. Выражение модификации на каждой итерации имеет вид :
![]()
Индексы k, k+1 означают предыдущую и текущую итерации соответственно.
Производная функции F11m(S11m) рассчитывается с использованием конечных разностей на конце линии с помощью выражения
![]()
где dτ соответствует времени задержки на одном шаге продольного разбиения (сегменте) линии длиной dz.
Итерации прекращаются, если удаётся сделать невязку Δср меньше ε.
Рассмотрим пример решения задачи частотного синтеза по четырем отсчётам S11(ωm,θ) распределённой линии с Т-волной. Волновое сопротивление трансформируется вдоль НЛП от 50 до 377 Ом. Подобная НЛП может быть использована в качестве многофункциональной СШП рупорной антенны с полосой пропускания 4 ГГц при средней частоте 4 ГГц, обеспечивающей подавление второй гармоники генератора с частотой сигнала 4 ГГц. Для этого на частоте 8 ГГц задан коэффициент отражения, равный 0.95. На частотах 2, 4, 6 ГГц коэффициент отражения задан равным нулю. Зависимость волнового сопротивления от продольной координаты синтезированной НЛП приведена на рис. 1.
|
ρ(τ), Ом
|

z,м
Рис.1. Зависимость волнового сопротивления синтезированной НЛП
от продольной координаты
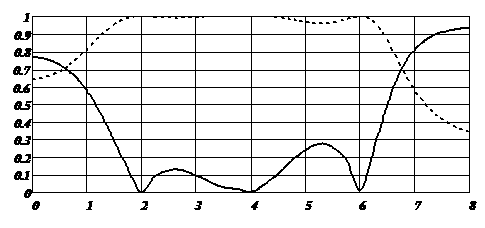
На рис. 2 и рис. 3 приведены частотные характеристики синтезированной НЛП, посчитанные по классической методике для каскадного соединения.
|
| S11(ω, θ)|,
| S21(ω, θ)|
|
f, ГГц
Рис. 2. АЧХ синтезированной НЛП
(сплошная линия - | S11(ω, θ)|, пунктирная - | S21(ω, θ)|)
|
arg(S11(ω, θ)),
arg(S21(ω, θ)),
рад
|
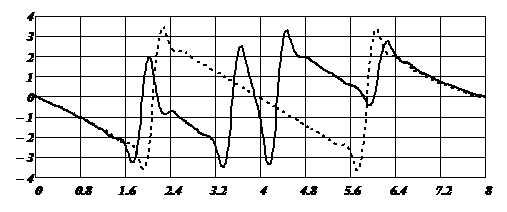
f, ГГц
Рис. 3. ФЧХ синтезированной НЛП
(сплошная линия - arg(S11(ω, θ)), пунктирная - arg(S21(ω, θ)))
Синтез линии был произведён за пятнадцать корректировочных итераций при заданной точности ε = 0.01. Конечная невязка составила Δср = 0.00925. Как видно из полученных результатов на рис.2, коэффициент отражения в полосе прозрачности НЛП не превосходит 0.3.
Описанная в работе методика численного синтеза позволяет решать самые разнообразные задачи. Область применимости методов анализа, построенных на основе полученных выражений достаточно широка. Метод гиперболического арктангенса, основанный на приближении (1), удобен из-за сокращения затрат машинного времени и возможности представить выражение для коэффициента отражения фактически в явном виде. Его недостаток – существенная ошибка для резко неоднородных ЛП.
Полезной и ценной оказывается возможность проводить синтез НЛП на отражение в частотной области, используя выражение (1), позволяющее получить начальное приближение, с дальнейшим применением алгоритмов численной корректировки. Описанным образом удаётся решать многие задачи синтеза недиссипативных НЛП с Т-волнами. Затруднения возникают в случае синтеза НЛП с квази-Т волнами, для которых фазовая скорость волны зависит от геометрических характеристик в поперечном сечении НЛП.
Литература
1. Чернышев С.Л. Приближенный аналитический синтез сверхширокополосных устройств на плавных нерегулярных линиях. Наука в образовании: электронное издание, 0420800025\0001, ╧1, 2008 .
2. Мещанов В.П., Тупикин В.Д., Чернышев С.Л. Коаксиальные пассивные устройства.-Саратов, Изд-во СГУ, 1993.
Публикации с ключевыми словами: синтез, нерегулярная линия передачи, сверхширокополосный, частотная область
Публикации со словами: синтез, нерегулярная линия передачи, сверхширокополосный, частотная область
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



