научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2009
УДК 519.6:621.39
МГТУ им. Н.Э.Баумана,
e-mail: chernshv@bmstu.ru
Расчет сверхширокополосных устройств, в том числе устройств фильтрации, излучения и др. на плавных нерегулярных линиях передачи (НЛП) с Т-волнами осуществляется с применением численных методов, так как отсутствуют аналитические методы расчета их конфигурации. В связи с этим происходит постоянный поиск наиболее эффективных методов их синтеза [1]. В данной статье рассматривается решение дифференциального уравнения плавной НЛП, которое значительно облегчает такой синтез.
В [2] было показано, что характеристики плавной НЛП описываются следующим нелинейным дифференциальным уравнением
 , (1)
, (1)
где ![]() - волновой коэффициент отражения от входа НЛП,
- волновой коэффициент отражения от входа НЛП, ![]() - время запаздывания волны, отраженной от произвольного сечения НЛП,
- время запаздывания волны, отраженной от произвольного сечения НЛП, ![]() - так называемая функция преобразования, связанная с функцией местных отражений НЛП
- так называемая функция преобразования, связанная с функцией местных отражений НЛП ![]() через преобразование Фурье [2]:
через преобразование Фурье [2]:
![]() .
.
Одной из наибольших сложностей является решение уравнения (1). Его решают численно. И это численное решение сходится тем быстрее, чем точнее найдено его начальное приближение. Найдем такое решение с применением степенных рядов. Для этого требуется разложить входящие в (1) сомножители в ряд Маклорена и приравнять коэффициенты получающихся при перемножении рядов при соответствующих степенях аргумента.
Для решения требуется получить выражения для нулевой, первой и второй производных ![]() по
по ![]() . Опустим для краткости записи аргументы этих функций.
. Опустим для краткости записи аргументы этих функций.
В [2] было показано, что при значениях ![]()
![]() . Таким образом, в окрестности нулевой точки можно положить, что
. Таким образом, в окрестности нулевой точки можно положить, что ![]() .
.
Значение второй производной найдем из уравнения (1), из которого видно, что при ![]()
 .
.
Для нахождения значения первой производной рассмотрим выражение для ![]() . Можно показать, что для плавной НЛП с малыми значениями местных коэффициентов отражения справедливо выражение
. Можно показать, что для плавной НЛП с малыми значениями местных коэффициентов отражения справедливо выражение
![]() , (2)
, (2)
где ![]() - характеристический полином, определяемый переотражениями между участками НЛП.
- характеристический полином, определяемый переотражениями между участками НЛП.
Используя (2), нетрудно получить, что
![]() .
.
Следовательно, при ![]()
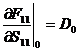 , где
, где ![]() при
при ![]() .
.
Таким образом, искомые производные найдены.
Теперь разложим сомножители, входящие в (1) в ряд Маклорена.
Левая часть (1) будет иметь вид
![]() , (3)
, (3)
где ![]() .
.
Первая производная из правой части имеет вид
![]()
![]() , (4)
, (4)
где ![]() , а
, а ![]() .
.
Сомножитель в правой части приобретает вид
 , (5)
, (5)
где ![]() ,
, ![]() .
.
Подставим ряды (3)-(4) в (1), раскроем скобки и приравняем коэффициенты при соответствующих степенях ![]() .
.
В итоге получаем
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
то есть четные производные при ![]() равны нулю, а нечетные производные при
равны нулю, а нечетные производные при ![]() равны
равны ![]() .
.
Полученные результаты позволяют определить зависимость ![]() .
.
Представим эту зависимость в виде ряда Маклорена:
![]() .
.
Производные, входящие в это выражение нами определены. После их подстановки получаем

Заметим, что в круглых скобках последнего выражения стоит выражение, совпадающее с разложением в ряд гиперболического арктангенса:
![]()
Таким образом, нами получен окончательный вид решения уравнения (1):
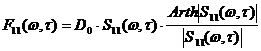 .
.
Это решение используется для быстрого численного решения уравнения (1) с итерационным уточнением коэффициента ![]() , начальное значение которого равно единице.
, начальное значение которого равно единице.
Литература
1. Чернышев С.Л. Приближенный аналитический синтез сверхширокополосных устройств на плавных нерегулярных линиях. Наука в образовании: электронное издание, 0420800025\0001, ╧1, 2008
2. Мещанов В.П., Тупикин В.Д., Чернышев С.Л. Коаксиальные пассивные устройства.-Саратов, Изд-во СГУ, 1993.
Публикации с ключевыми словами: нерегулярная линия передачи
Публикации со словами: нерегулярная линия передачи
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



