научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2013
DOI: 10.7463/1113.0623564
УДК 539.3
Россия, МГТУ им. Н.Э. Баумана
Введение
Композиционные материалы на основе неорганических связующих (фосфатных, алюмо-фосфатных, хромо-фосфатных, магний-фосфатных, алюмо-хромофосфатных (АХФС) представляют собой перспективных класс конструкционных материалов для создания теплонагруженных конструкций [1-6]. Материалы данного класса сохраняют работоспособность до температуры 1500 °С без оплавления, имеют хорошие диэлектрические характеристики во всем интервале рабочих температур, относительно высокие прочностные показатели при температурах до 800 °С, обладают термостойкостью в окислительных средах, повышенной ударной вязкостью [7-9].
Одним из перспективных типов композиционных материалов на неорганической матрицы являются композиты на основе кварцевой ткани и матрицы из АХФС с добавлением мелкодисперсный наполнителей в виде порошка электроплавленного корунда ![]() и керамики
и керамики ![]() [6]. При высоких температурах в матрице и волокнах композитов на основе АХФС происходят сложные фазовые превращения, приводящие к необратимому изменению всех тепломеханических и теплофизических свойств материала. Вообще говоря, композиты на основе неорганических матриц при высоких температурах представляют собой многофазную систему, состоящую из нескольких твёрдых фаз, механически и химически взаимодействующих между собой.
[6]. При высоких температурах в матрице и волокнах композитов на основе АХФС происходят сложные фазовые превращения, приводящие к необратимому изменению всех тепломеханических и теплофизических свойств материала. Вообще говоря, композиты на основе неорганических матриц при высоких температурах представляют собой многофазную систему, состоящую из нескольких твёрдых фаз, механически и химически взаимодействующих между собой.
Математические модели термомеханического поведения композитов на неорганических матрицах были разработаны в [7-9], в работе [9] была предложена многомасштабная модель внутренней структуры алюмо-фосфатного композита. Цель настоящей работы – построение математической модели композитов на основе АХФС, позволяющей более детально описать переменную микроструктуру многофазного композита с учетом кинетики процессов, протекающих в композиционных материалах на АХФ связующих при высоких температурах, а также позволяющей прогнозировать зависимость модулей упругости и пределов прочности материала от режима температурного нагрева. При создании этой модели использован опыт разработки моделей термомеханического высокотемпературного поведения композиционных материалов на полимерных матрицах [10-13].
Многоуровневая модель композиционных материалов на АХФ матрице при высоких температурах. Тканевые композиционные материалы на АХФ матрице рассмотрим как многоуровневую структуру, состоящую из 4-х структурных уровней (Рис. 1). Каждый структурный уровень состоит из большого числа соответствующих ячеек периодичности (ЯП).

Рис. 1. Многоуровневая модель структуры КМ на АХФС
ЯП 1-го структурного уровня состоит из 2-х элементов: тканевого наполнителя на основе переплетенных нитей и АХФ матрицы. Нити в ткани состоят из большого числа моноволокон, соединенных матрицей, поэтому введем ЯП 2-го структурного уровня – ЯП2b, состоящую из 1 моноволокна, окруженного матрицей. Сама АХФ матрица также представляет собой композитную структуру – она состоит собственно из АХФС и дисперсных керамических частиц на основе оксидов алюминия и хрома: ![]() и
и ![]() , поэтому матрицу полагаем состоящей из ЯП2а (рис.1). При высоких температурах в моноволокнах и АХФС происходят фазовые превращения, поэтому и матрицу и моноволокна полагаем состоящими из ЯП3а и ЯП3b, соответственно. Фазовые превращения в стеклянных волокнах при нагреве происходят по механизму роста кристобаллитной фазы и уменьшения исходной аморфной фазы стекловолокна, поэтому ЯП3b состоит из 2-х фаз: аморфной (h-фаза) и кристаллической (l-фаза) (рис. 1). ЯП3а состоит из 2-х фаз: одна соответствует той части связующего, для которой фазовые превращения происходят по алюмосодержащей цепочке (рис. 2), а вторая – по хромосодержащей цепочке.
, поэтому матрицу полагаем состоящей из ЯП2а (рис.1). При высоких температурах в моноволокнах и АХФС происходят фазовые превращения, поэтому и матрицу и моноволокна полагаем состоящими из ЯП3а и ЯП3b, соответственно. Фазовые превращения в стеклянных волокнах при нагреве происходят по механизму роста кристобаллитной фазы и уменьшения исходной аморфной фазы стекловолокна, поэтому ЯП3b состоит из 2-х фаз: аморфной (h-фаза) и кристаллической (l-фаза) (рис. 1). ЯП3а состоит из 2-х фаз: одна соответствует той части связующего, для которой фазовые превращения происходят по алюмосодержащей цепочке (рис. 2), а вторая – по хромосодержащей цепочке.
Каждая из этих фаз 3-его уровня, в свою очередь, представляется в виде 5-фазной системы. При нагреве до высоких температур происходит перераспределение соотношения между этими фазами. Схема фазовых превращений в АХФС [2] на 4-м структурном уровне показана на рисунке 2.
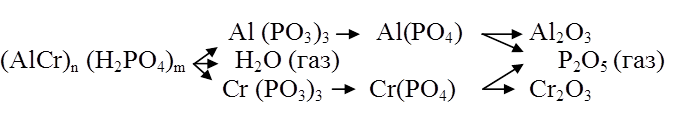
Рис. 2. Схема фазовых превращений в АХФС при нагреве до 1500 К
Введем следующие обозначения для фаз КМ. На 1-м структурном уровне: ![]() – это содержание армирующих тканевых нитей и матрицы – составляющих ЯП 1 (
– это содержание армирующих тканевых нитей и матрицы – составляющих ЯП 1 (![]() ). эти концентрации не меняются при нагреве:
). эти концентрации не меняются при нагреве:![]() На 2-м структурном уровне в ЯП2а:
На 2-м структурном уровне в ЯП2а: ![]() ,
,![]() ,
,![]() – концентрации керамических включений
– концентрации керамических включений ![]() ,
, ![]() и АХФС в матрице (
и АХФС в матрице (![]() ), а в ЯП2b:
), а в ЯП2b: ![]() – относительное содержание моноволокна и окружающей его части АХФ матрицы. В ЯП3b:
– относительное содержание моноволокна и окружающей его части АХФ матрицы. В ЯП3b: ![]() – это относительные концентрации аморфной и кристаллической фазы волокон, которые связаны соотношением:
– это относительные концентрации аморфной и кристаллической фазы волокон, которые связаны соотношением: ![]() .Концентрации фаз в ЯП3а обозначим следующим образом:
.Концентрации фаз в ЯП3а обозначим следующим образом: ![]() (
(![]() ), их значения таковы:
), их значения таковы: ![]()
![]() .
.
Для фаз ЯП 4-го уровня – ЯП4a и ЯП4bвведем обозначения:![]() – объемная концентрация полимерной фазы
– объемная концентрация полимерной фазы ![]() ,
, ![]() – объемная концентрация метафосфатной фазы
– объемная концентрация метафосфатной фазы ![]() ,
, ![]() – объемная концентрация ортофосфатной фазы
– объемная концентрация ортофосфатной фазы ![]() ,
, ![]() – объемная концентрация керамической фазы
– объемная концентрация керамической фазы ![]() ,
, ![]() – объемная концентрация газовой фазы
– объемная концентрация газовой фазы ![]() . Все эти фазы связаны соотношением:
. Все эти фазы связаны соотношением:
 (1)
(1)
индекс ![]() соответствует алюмосодержащей цепочке, а индекс
соответствует алюмосодержащей цепочке, а индекс ![]() – хромосодержащей цепочке фаз АХФС.
– хромосодержащей цепочке фаз АХФС.
Математическая модель изменения фазового состава АХФС в ЯП 4-ого уровня при нагреве. Математические модели алюмо- и хромсодержащей цепочек превращения АХФС в ЯП4а и ЯП4bбудем рассматривать как отдельные, но аналогичные друг другу. Система уравнений для расчета объёмных концентраций фаз в ЯП4а и ЯП4bследует из системы законов сохранения масс фаз:
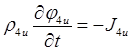

 (2)
(2)
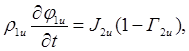

где обозначены: ![]() – плотности фаз (полагаются постоянными, кроме плотности газовой фазы
– плотности фаз (полагаются постоянными, кроме плотности газовой фазы ![]() ),
), ![]() – вектор скорости движения газовой фазы,
– вектор скорости движения газовой фазы, ![]() – коэффициенты газификации,
– коэффициенты газификации, ![]() – массовые скорости фазовых превращений, для которых имеют место соотношения Аррениуса:
– массовые скорости фазовых превращений, для которых имеют место соотношения Аррениуса:
 (3)
(3)
здесь ![]() – энергии активации фазовых превращений,
– энергии активации фазовых превращений, ![]() – предэкспоненциальные множители, R– газовая постоянная.
– предэкспоненциальные множители, R– газовая постоянная.
Модель для расчета упругих свойств матрицы в ЯП 4-го уровня при нагреве. Рассмотрим модельную форму ЯП4а и ЯП4b, в которой каждая фаза имеет форму пустотелого куба, а газовая фаза – сплошного куба. Оси локальной системы координат ![]() ориентированы так, как показано на рисунке 2. Выделим 1/2 ЯП4а, принадлежащую полуплоскости
ориентированы так, как показано на рисунке 2. Выделим 1/2 ЯП4а, принадлежащую полуплоскости ![]() и разделим ее на 5 частей плоскостями
и разделим ее на 5 частей плоскостями![]() , совпадающими с границами раздела фаз. Тогда каждый такой j-й слой содержит j фаз. Используя принцип сложения слоёв [14] при одноосном напряженном состоянии в направлении оси
, совпадающими с границами раздела фаз. Тогда каждый такой j-й слой содержит j фаз. Используя принцип сложения слоёв [14] при одноосном напряженном состоянии в направлении оси ![]() , вычисляем сначала эффективные модули упругости
, вычисляем сначала эффективные модули упругости ![]() каждого j-го слоя, полагая, что деформации растяжения
каждого j-го слоя, полагая, что деформации растяжения ![]() в направлении
в направлении ![]() в разных фазах внутри каждого j-го слоя совпадают с деформацией слоя
в разных фазах внутри каждого j-го слоя совпадают с деформацией слоя ![]() , а нормальные напряжения
, а нормальные напряжения ![]() в направлении
в направлении ![]() в каждом слое представляют собой сумму напряжений в фазах
в каждом слое представляют собой сумму напряжений в фазах ![]() , тогда имеют место следующие соотношения
, тогда имеют место следующие соотношения
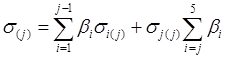
![]()
![]()
![]()
 (4)
(4)
здесь ![]() – модули упругости фаз,
– модули упругости фаз, ![]() и
и ![]() – осредненное напряжение и осредненная деформация в ЯП4а или ЯП4b,
– осредненное напряжение и осредненная деформация в ЯП4а или ЯП4b, ![]() – относительные толщины слоев (
– относительные толщины слоев ( ),
), ![]() – относительные площади сечений фаз плоскостью
– относительные площади сечений фаз плоскостью ![]() , которые связаны с концентрациями фаз следующими соотношениями:
, которые связаны с концентрациями фаз следующими соотношениями:
![]()
![]() (5)
(5)
![]() .
.
С помощью соотношений (4) вычисляем эффективные модули упругости матрицы ![]() в ЯП4а или ЯП4b,связывающие напряжения
в ЯП4а или ЯП4b,связывающие напряжения ![]() и деформации
и деформации ![]() законом Гука
законом Гука ![]() :
:
 ,
, 
![]() (6)
(6)
Модули упругости ![]() фаз полагаем постоянными, а модули упругости
фаз полагаем постоянными, а модули упругости ![]() керамической фазы C при высоких температурах изменяются согласно степенной зависимости
керамической фазы C при высоких температурах изменяются согласно степенной зависимости
 (7)
(7)

Рис. 3. Схема ячейки периодичности ![]() ЯП4а и ЯП4b
ЯП4а и ЯП4b
Модель для расчета упругих свойств АХФС на 3-м уровне. На 3-м структурном уровне в рамках ЯП3а осуществляется соединение алюмосодержащих и хромосодержащих фаз матрицы. В этих целях для ЯП3 используем указанную выше модель ячейки периодичности с кубической формой фаз, тогда для эффективного модуля упругости АХФС на 3-м уровне ![]() получаем формулы, аналогичные формулам (6):
получаем формулы, аналогичные формулам (6):
![]()
![]() (8)
(8)
![]()
![]()
Модель изменения упругих свойств стеклянных моноволокон в ЯП3 при нагреве. Изменение объемной концентрации аморфной h-фазы стеклянных волокон описывается уравнениями сохранения масс:

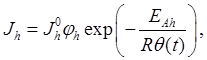 (9)
(9)
где: ![]() – плотность аморфной фазы,
– плотность аморфной фазы, ![]() – энергия активации аморфной фазы,
– энергия активации аморфной фазы, ![]() – предэкспоненциальный множитель. Концентрация кристаллической фазы находится с помощью соотношения
– предэкспоненциальный множитель. Концентрация кристаллической фазы находится с помощью соотношения ![]() .
.
Изменение модуля упругости для стеклянных волокон при нагреве определяется двумя факторами: 1) изменением упругих свойств волокна в аморфном состоянии при относительно низких температурах; 2) физико-химическими процессами кристаллизации при высоких температурах. Первый фактор вызывает обратимое изменение модуля упругости ![]() волокон, второй – приводит к необратимым к изменениям после охлаждения.
волокон, второй – приводит к необратимым к изменениям после охлаждения.
Используя для ЯП3bуказанную выше модель ячейки периодичности с кубической формой фаз, для модуля упругости ![]() . моноволокон получаем следующие выражения:
. моноволокон получаем следующие выражения:
![]()
![]() (10)
(10)
![]()
![]()
Для учета обратимого изменения упругих свойств волокон модуль упругости аморфной фазы волокон полагаем зависящим от температуры, согласно модели, предложенной в [10]:
![]()
![]() (11)
(11)
где ![]() ,
, ![]() – константы модели.
– константы модели.
Модель для расчета упругих характеристик 1Dкомпозита на 2-м уровне.
ЯП2b (1-D элемент) представляет собой одно моноволокно цилиндрической формы, окруженное АХФ матрицей (рис. 4).
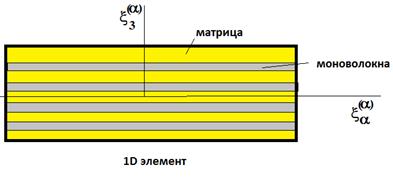
Рис. 4. Геометрия ЯП2b 1-Dэлемента
Данный тип материала является трансверсально-изотропным, в связи с этим, у 1D-элемента не один эффективный модуль упругости, как у изотропной матрицы, а два: продольный и поперечный. Всего у 1-D элемента 5 независимых упругих констант, для их вычисления используем смесевые формулы [10, 15, 16]:
![]() ,
, 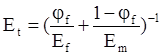 ,
,
![]() ,
, ![]() , (12)
, (12)
 ,
,
где ![]() – продольный модуль упругости нити в направлении ее укладки,
– продольный модуль упругости нити в направлении ее укладки, ![]() – поперечный модуль упругости нити,
– поперечный модуль упругости нити, ![]() – продольный коэффициент Пуассона,
– продольный коэффициент Пуассона, ![]() – поперечный коэффициент Пуассона нити,
– поперечный коэффициент Пуассона нити, ![]() – продольный модуль сдвига,
– продольный модуль сдвига,  – поперечный модуль сдвига нити. В формулах (3) обозначены:
– поперечный модуль сдвига нити. В формулах (3) обозначены: ![]() – модули упругости моноволокон,
– модули упругости моноволокон, ![]() – коэффициент Пуассона моноволокон,
– коэффициент Пуассона моноволокон, ![]() – продольный модуль сдвига моноволокон,
– продольный модуль сдвига моноволокон, ![]() и
и ![]() – модуль упругости и коэффициент Пуассона матрицы,
– модуль упругости и коэффициент Пуассона матрицы, ![]() – относительное объемное содержание моноволокон в 1D элементе. Вместо смесевых формул (3) можно использовать более точные формулы расчета эффективных упругих характеристик однонаправленных композитов, основанные на численном решении таких же локальных задач на ЯП низшего структурного уровня, этот подход рассматривался в работе [15,16]. В данной работе в целях создания более эффективного вычислительного алгоритма, были использованы более простые смесевые формулы (12).
– относительное объемное содержание моноволокон в 1D элементе. Вместо смесевых формул (3) можно использовать более точные формулы расчета эффективных упругих характеристик однонаправленных композитов, основанные на численном решении таких же локальных задач на ЯП низшего структурного уровня, этот подход рассматривался в работе [15,16]. В данной работе в целях создания более эффективного вычислительного алгоритма, были использованы более простые смесевые формулы (12).
Модель для расчета упругих характеристик матрицы на 2-м уровне.
Для расчета эффективного модуля упругости матрицы на 2-м структурном уровне также воспользуемся кубической моделью, полагая, что упругие модули керамики на основе Al2O3 и Cr2O3 близки, тогда используя формулы (6), получаем для эффективного модуля упругости АХФ матрицы:
![]()
![]() (13)
(13)
![]()
![]()
Здесь ![]() – модуль упругости керамических частиц.
– модуль упругости керамических частиц.
Методика расчета эффективных упругих характеристик тканевого композита в ЯП1. 1-й и 2-й структурный уровни отличаются от уровней 3 и 4 тем, что для ЯП1 и ЯП2 известна достаточно четко оформленная стабильная геометрическая микроструктура фаз "искусственного" происхождения, образованная нитями, сплетенными в ткань (ЯП1), моноволокнами, собранными в нити (ЯП2b) и керамическими частицами (ЯП2a). Для расчета упругих характеристик на 1-м и 2-м уровнях можно применять более точные конечно-элементные методы [17]. В целях сокращения вычислительных затрат для расчета эффективных упругих характеристик в ЯП 2-го уровня выше были применены приближенные методы, но для ЯП объединяющего 1-го уровня применим именно конечно-элементный метод, основанный на методе асимптотического осреднения [18,19].
Согласно этому методу для ЯП1 сформулируем серию так называемых локальных задач Lpq теории упругости на 1/8 части ЯП1 ![]() [15,16]
[15,16]
 (14)
(14)
где p, q – индексы задач, изменяющиеся в пределах от 1 до 3 (всего имеется 9 различных задач Lpq), ![]() – компоненты векторов перемещений (искомые неизвестные функции задачи) в задаче Lpq ,
– компоненты векторов перемещений (искомые неизвестные функции задачи) в задаче Lpq , ![]() ,
, ![]() – компоненты тензоров напряжений и деформаций в ЯП,
– компоненты тензоров напряжений и деформаций в ЯП, ![]() - «локальные» декартовы координаты в ЯП,
- «локальные» декартовы координаты в ЯП, ![]() - производные по локальным координатам,
- производные по локальным координатам, ![]() – скачки функций на поверхностях раздела
– скачки функций на поверхностях раздела ![]() компонентов композита, где
компонентов композита, где ![]() – номера армирующих компонентов (нитей) композита,
– номера армирующих компонентов (нитей) композита, ![]() – индекс, соответствующий матрице композита (для ткани с полотняным или саржевым переплетением
– индекс, соответствующий матрице композита (для ткани с полотняным или саржевым переплетением ![]() ),
), ![]() – компоненты тензоров модулей упругости структурных компонентов композита (их различие для разных компонент - нитей и матрицы, описывает зависимость от координат
– компоненты тензоров модулей упругости структурных компонентов композита (их различие для разных компонент - нитей и матрицы, описывает зависимость от координат![]() ).
).
Система (14) дополняется специальными граничными условиями на торцевых поверхностях ![]() 1/8 ЯП:
1/8 ЯП:
 ,
,
 (15)
(15)
![]()
Граничные условия на плоскостях симметрии ![]() имеют вид аналогичный соотношениям (15), в которых следует положить
имеют вид аналогичный соотношениям (15), в которых следует положить ![]() , где
, где ![]() – осредненные деформации по ЯП, являющиеся входными данными для задачи Lpq.
– осредненные деформации по ЯП, являющиеся входными данными для задачи Lpq.
Для вычисления компонент тензоров модулей упругости нитей ![]() (
(![]() – область в ЯП, занятая
– область в ЯП, занятая ![]() -й нитью в системе координат
-й нитью в системе координат ![]() ,связанной с ЯП) воспользуемся моделью [20], в которой каждая нить (являющаяся криволинейно-трансверсально изотропным материалом) рассматривается как система большого числа элементарных нитевых сегментов (ЭНС), на которые
,связанной с ЯП) воспользуемся моделью [20], в которой каждая нить (являющаяся криволинейно-трансверсально изотропным материалом) рассматривается как система большого числа элементарных нитевых сегментов (ЭНС), на которые ![]() -ю нить делят плоскости, ортогональные к оси
-ю нить делят плоскости, ортогональные к оси ![]() (рис. 5). Введем новую декартову прямоугольную систему координат
(рис. 5). Введем новую декартову прямоугольную систему координат ![]() – назовем ее "собственную системой координат ЭНС", точка начала
– назовем ее "собственную системой координат ЭНС", точка начала ![]() которой принадлежит линии центров тяжести нити, а ось
которой принадлежит линии центров тяжести нити, а ось ![]() повернута по отношению к оси
повернута по отношению к оси ![]() единой для ЯП1 локальной системы координат на угол
единой для ЯП1 локальной системы координат на угол ![]() , меняющийся вдоль одной координаты
, меняющийся вдоль одной координаты ![]() , т.е поворот собственной системы координат
, т.е поворот собственной системы координат ![]() осуществляется вокруг оси
осуществляется вокруг оси ![]() . В собственной системе координат
. В собственной системе координат ![]() каждый ЭНС будем считать трансверсально-изотропным 1D- элементом, тогда его упругие характеристики в
каждый ЭНС будем считать трансверсально-изотропным 1D- элементом, тогда его упругие характеристики в ![]() вычисляются по формулам (12).
вычисляются по формулам (12).

Рис. 5. Модель изогнутой нити в тканевом композите
По этим значениям упругих констант составим тензоры упругих податливостей ![]() нитей в собственных системах координат
нитей в собственных системах координат ![]() , используя матричное представление тензоров упругих податливостей [21]
, используя матричное представление тензоров упругих податливостей [21]
 (16)
(16)
Тензор модулей упругости нитей в собственной системе координат ![]() является обратным для тензора упругих податливостей:
является обратным для тензора упругих податливостей: ![]() . Для нахождения компонент тензора модулей упругости нити в единой системе координат
. Для нахождения компонент тензора модулей упругости нити в единой системе координат ![]() используем формулы преобразования компонент тензора 4-го ранга при повороте системы координат на угол
используем формулы преобразования компонент тензора 4-го ранга при повороте системы координат на угол ![]() [22]
[22]
![]() , (17)
, (17)
где ![]() - матрицы поворота системы координат
- матрицы поворота системы координат ![]() относительно
относительно ![]() .
.
Матрица композита (компонент с номером ![]() ) является изотропной, ее тензор упругих податливостей
) является изотропной, ее тензор упругих податливостей ![]() одинаков в собственной и единой системах координат, и выражается через технические упругие константы стандартным образом [21, 22]:
одинаков в собственной и единой системах координат, и выражается через технические упругие константы стандартным образом [21, 22]:
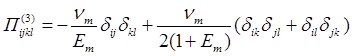 , (18)
, (18)
Для определения компонент тензора эффективных модулей упругости композита ![]() , связывающего осредненные по ЯП1 напряжения и деформации композита:
, связывающего осредненные по ЯП1 напряжения и деформации композита: ![]() , воспользуемся решением серии локальных задач
, воспользуемся решением серии локальных задач ![]() (14), (15). Методика численного конечно-элементного их решения описана в [17, 23, 24], после численного решения задач
(14), (15). Методика численного конечно-элементного их решения описана в [17, 23, 24], после численного решения задач ![]() находим поля перемещений
находим поля перемещений ![]() и напряжений
и напряжений ![]() в ЯП при заданных значениях средних деформаций
в ЯП при заданных значениях средних деформаций ![]() . По этим полям вычисляем средние напряжения
. По этим полям вычисляем средние напряжения
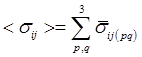 , где:
, где: 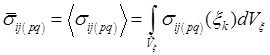 , (19)
, (19)
тогда компоненты тензора эффективных модулей упругости композита вычисляются по формулам
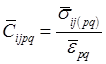 , (20)
, (20)
где по p и q суммирования нет. После расчета тензора модулей упругости ![]() рассчитывается эффективный тензор упругих податливостей
рассчитывается эффективный тензор упругих податливостей ![]() , являющийся обратным к
, являющийся обратным к ![]() , в результате находим девять технических упругих констант композита:
, в результате находим девять технических упругих констант композита: ![]() – эффективные модули Юнга;
– эффективные модули Юнга; ![]() – эффективные коэффициенты Пуассона;
– эффективные коэффициенты Пуассона; ![]() – эффективные модули сдвига.
– эффективные модули сдвига.
Методики численного моделирования композитов на неорганической матрице.
Для нахождения распределения объемных концентраций матрицы в ЯП 4-го уровня и дальнейшего вычисления модуля упругости матрицы и моноволокон в зависимости от температуры нагрева использовался неявный метод Эйлера решения систем ОДУ (2) и (9). Модуль упругости матрицы и волокон при различных температурах вычислялся по аналитическим формулам (4)-(8), (10)-(13). Для решения локальных задач (14), (15) в ЯП1 применялся метод конечного элемента. Все вышеизложенные методы решения задач были реализованы в среде программирования MicrosoftVisualC++ 2008. Численное решение больших систем линейных алгебраических уравнений методами сопряженных градиентов, препроцессинг и постпроцессинг, в том числе 3D визуализация осуществлялись в программном комплексе, разработанном в научно-образовательном центре «Суперкомпьютерное инженерное моделирование и разработка программных комплексов» МГТУ им. Н.Э. Баумана [23, 24].
Следует отметить, что в настоящее время в литературе отсутствуют систематизированные экспериментальные данные по характеристикам фаз АХФС, поэтому фактически целью вычислительной части данной работы было исследование вопроса - существуют ли такие значения параметров предложенной модели АХФС, которые обеспечивают адекватное описание температурных зависимостей упругих характеристик тканевых композитов на основе АХФС. Более детальное исследование данной проблемы, - восстановление истинных значений характеристик фаз АХФС, приводящее к необходимости решения обратных задач, целесообразно реализовывать только после указанных предварительных исследований, демонстрирующих принципиальную адекватность разработанной модели. Решение обратных задач планируется в дальнейших исследованиях по данной проблеме.
Результаты численного моделирования. Расчеты проводились для случая равномерного линейный нагрева по закону: ![]() со скоростью
со скоростью ![]() до температуры 1600К. Ввиду отсутствия достоверных данных о характеристиках фаз был сделан ряд допущений: плотности
до температуры 1600К. Ввиду отсутствия достоверных данных о характеристиках фаз был сделан ряд допущений: плотности ![]() фаз АХФС в ЯП 4-го уровня были приняты одинаковыми. Энергии активации фаз
фаз АХФС в ЯП 4-го уровня были приняты одинаковыми. Энергии активации фаз ![]() и предэкспоненциальные множители
и предэкспоненциальные множители ![]() фаз подбирались таким образом, чтобы существование каждой из фаз при линейном нагреве соответствовало определенному температурному диапазону, который известен для типичного состава АХФС [1, 2]. Значения полученных таким образом характеристик фаз представлены в таблице 1. На рисунках 6 и 7 показаны графики изменения концентраций фаз
фаз подбирались таким образом, чтобы существование каждой из фаз при линейном нагреве соответствовало определенному температурному диапазону, который известен для типичного состава АХФС [1, 2]. Значения полученных таким образом характеристик фаз представлены в таблице 1. На рисунках 6 и 7 показаны графики изменения концентраций фаз ![]() по алюмосодержащей и хромосодержащей цепочкам АХФС при линейном нагреве. Константы, характеризующие характер убывания модуля упругости керамической фазы были выбраны равными
по алюмосодержащей и хромосодержащей цепочкам АХФС при линейном нагреве. Константы, характеризующие характер убывания модуля упругости керамической фазы были выбраны равными ![]() .
.
Значения характеристик фаз стеклянных волокон взяты из работы [10], эти константы представлены в табл. 2. Изменение объемные концентраций фаз стеклянного волокна при нагреве показано на рис. 8.
Таблица 1. Характеристики фаз АХФС в ЯП4.
Фазы/(№ фазы) |
| Характеристики | |||
|
|
|
| Г | |
| 2000 | 5600 | 300000 | 10 | 0,05 |
| 2000 | 8000 | 191000 | 25 | - |
| 2000 | 8200 | 30000 | 20 | - |
| 2000 | 10000 | 300000 | 35 | - |
| 2000 | 10500 | 30000 | 30 | - |
| 2000 | - | - | 45 | 0.05 |
| 2000 | - | - | 40 | 0.05 |
Таблица 2. Характеристики фаз стеклянных волокон, ![]() – аморфная фаза,
– аморфная фаза, ![]() – кристаллическая фаза.
– кристаллическая фаза.
Фазы |
| Характеристики | ||
|
|
|
| |
Аморфная | 2200 | 7000 | 6600 | 80 |
Кристаллическая | 2000 | - | - | 1 |

Рис. 6. Объемные концентрации ![]() АХФС по алюмосодержащей цепочке: полимерной фазы (1), метафосфатной фазы (2), ортофосфатной фазы (3), керамической фазы (4), газовой фазы (5)
АХФС по алюмосодержащей цепочке: полимерной фазы (1), метафосфатной фазы (2), ортофосфатной фазы (3), керамической фазы (4), газовой фазы (5)

Рис. 7. Объемные концентрации ![]() АХФС по хромосодержащей цепочке: полимерной фазы (1), метафосфатной фазы (2), ортофосфатной фазы (3), керамической фазы (4), газовой фазы (5)
АХФС по хромосодержащей цепочке: полимерной фазы (1), метафосфатной фазы (2), ортофосфатной фазы (3), керамической фазы (4), газовой фазы (5)

Рис. 8.Изменение объемные концентраций фаз ![]() стеклянного волокна при нагреве: аморфная фаза (1), кристаллическая фаза (2)
стеклянного волокна при нагреве: аморфная фаза (1), кристаллическая фаза (2)
На рисунке 9 показан график изменения модуля упругости АХФС ![]() при линейном нагреве, рассчитанный с помощью соотношений (8). Ввиду того, что графики изменения модуля упругости связующего АХФС при нагреве не были известны, значения модулей упругости фаз, использованные в этих расчетах, подбирались таким образом, чтобы обеспечить наилучшее совпадение расчетных кривых изменения модуля упругости тканевого композита на основе АХФС. График изменения модуля упругости кварцевого волокна в зависимости от температуры, рассчитанный по формулам (9)-(11), показан на рис. 10.
при линейном нагреве, рассчитанный с помощью соотношений (8). Ввиду того, что графики изменения модуля упругости связующего АХФС при нагреве не были известны, значения модулей упругости фаз, использованные в этих расчетах, подбирались таким образом, чтобы обеспечить наилучшее совпадение расчетных кривых изменения модуля упругости тканевого композита на основе АХФС. График изменения модуля упругости кварцевого волокна в зависимости от температуры, рассчитанный по формулам (9)-(11), показан на рис. 10.

Рис. 9. Модуль упругости АХФС ![]() (2), модуль упругости матрицы по хромосодержащей цепочке (1), модуль упругости матрицы по алюмосодержащей цепочке (3)
(2), модуль упругости матрицы по хромосодержащей цепочке (1), модуль упругости матрицы по алюмосодержащей цепочке (3)

Рис.10. Модуль упругости ![]() кварцевого волокна в зависимости от температуры.
кварцевого волокна в зависимости от температуры.
Далее, учитывая полученные модули упругости, были рассчитаны эффективные упругие характеристики матрицы 2-го уровня с помощью МАО и МКЭ. Объемная доля включений (коэффициент армирования) в ЯП на 2-м уровне был принят равным 0.1. Последним шагом алгоритма является расчет эффективного модуля упругости всего тканевого композита и сравнение с экспериментальными данными. На рисунке 11 показаны расчетная и экспериментальная кривые изменения модуля упругости ![]() тканевого композита в направлении укладки волокон (по основе ткани). Достигнутая точность моделирования находится в приемлемом, для поставленных задач, диапазоне значений. разработанная модель композита позволяет прогнозировать эффект повышения упругих свойств композита при нагреве до температур
тканевого композита в направлении укладки волокон (по основе ткани). Достигнутая точность моделирования находится в приемлемом, для поставленных задач, диапазоне значений. разработанная модель композита позволяет прогнозировать эффект повышения упругих свойств композита при нагреве до температур ![]() , а также снижение модуля упругости при дальнейшем нагреве в области
, а также снижение модуля упругости при дальнейшем нагреве в области ![]() .
.

Рис. 11.Изменение модуля ![]() упругости тканевого композита на основе АХФС при нагреве, 1 –экспериментальные значения [9], 2 – численный расчёт.
упругости тканевого композита на основе АХФС при нагреве, 1 –экспериментальные значения [9], 2 – численный расчёт.
Выводы
Разработана математическая модель процессов, протекающих в композиционном материале на неорганическом алюмо-хромофосфатном связующем при высоких температурах, которая позволяет прогнозировать сложный нелинейный характер зависимости упругих характеристик композиционного материала от температурного режима нагрева.
Сравнение результатов расчетов с экспериментальными данными позволяет говорить о вполне удовлетворительной точности разработанной модели. С помощью проведенных численных расчетов определены характерные значения характеристик материала – констант модели.
Разработанная модель может быть применена для прогнозирования изменения упругих характеристик композиционных материалов на неорганической матрице при сложных режимах нагрева, что позволяет сократить необходимый объем экспериментальных исследований.
Список литературы
1. Абзгильдин Ф.Ю., Тесвятский С.Г. Асбофосфатные материалы. Киев, Наукова думка, 1980. 99 с.
2. Технология и свойства фосфатных материалов / Под ред. В.А. Копейкина. М.: Стройиздат, 1974. 224 с.
3. Сычев М.М. Неорганические клеи. Л., Химия, 1974.
4. Толстогузов В.Б. Неорганические полимеры. М.: Наука, 1967. 191 с.
5. Копейкин В.А., Петрова А.П., Рашкован И.П. Материалы на основе металлофосфатов. М.: Химия, 1976. 199 с.
6. Епифановский И.С., Димитриенко Ю.И., Ширяев А.В. Композиция для керамического электроизоляционного материала: пат. 2028993 РФ.1995.
7. Dimitrienko Yu.I., Epifanovsky I.S. Investigation of High Temperature Deformations of Composites on an Inorganic Matrix // Moscow International Composites Conference 1990 (MICC 90) / I.N. Fridlyander,V.I. Kostikov (eds.). Springer, 1991. P.1206-1210. DOI: 10.1007/978-94-011-3676-1_232
8. Димитриенко Ю.И., Епифановский И.С. Математическое моделирование процессов образования технологических напряжений в элементах конструкций из минеральных текстолитов // Композиционные материалы в изделиях машиностроения: материалы конференции. Реутов, НПО Машиностроения,1989. С. 23-28.
9. Dimitrienko Yu.I. Inorganic Matrix Composite Materials: Peculiarities, modelling, testing // ECC8. European Conf. on Composite Materials. Science. Technology and Applications (3-6 June 1998, Napoli, Italy). WoodHead Publishing Limited. 1998. Vol. 4. P. 201-208.
10. Димитриенко Ю.И. Механика композиционных материалов при высоких температурах. М.: Машиностроение, 1997.368 с.
11. Димитриенко Ю.И., Минин В.В., Сыздыков Е.К. Численное моделирование процессов тепломассопереноса и кинетики напряжений в термодеструктирующих композитных оболочках // Вычислительные технологии. 2012. Т. 17, № 2. С.43-59.
12. Димитриенко Ю.И., Минин В.В., Сыздыков Е.К. Моделирование внутреннего тепломассопереноса и термонапряжений в композитных оболочках при локальном нагреве // Математическое моделирование. 2011. Т. 23, № 9. С. 14-32.
13. Димитриенко Ю.И., Минин В.В., Сыздыков Е.К. Моделирование термомеханических процессов в композитных оболочках при локальном нагреве излучением // Механика композиционных материалов и конструкций. 2011. Т. 17, № 1. С. 71-91.
14. Тарнопольский Ю.М., Жигун И.Г., Поляков В.А. Пространственно-армированные композиционные материалы. М.: Машиностроение. 1987. 224 с.
15. Димитриенко Ю.И., Соколов А.П. Многомасштабное моделирование упругих композиционных материалов // Математическое моделирование. 2012. Т. 24, № 5. С. 3-20.
16. Димитриенко Ю.И., Соколов А.П. Численное моделирование композиционных материалов с многоуровневой структурой // Известия РАН. Серия физическая. 2011. Т. 75, № 11. С. 1549-1554.
17. Димитриенко Ю.И., Соколов А.П. Метод конечных элементов для решения локальных задач механики композиционных материалов. М.: МГТУ им. Н.Э. Баумана, 2010. 66 с.
18. Бахвалов Н.С., Панасенко Г.П. Осреднение процессов в периодических средах. М.: Наука, 1984. 352 с.
19. Победря Б.Е. Механика композиционных материалов. М.: Изд-во МГУ, 1984. 334 с.
20. Димитриенко Ю.И., Соколов А.П., Сборщиков С.В. Моделирование микро-разрушения тканевых композитов // Инженерный журнал: наука и инновации. 2012. № 2. Режим доступа: http://engjournal.ru/catalog/mathmodel/material/32.html (дата обращения 01.10.2013).
21. Димитриенко Ю.И. Механика сплошной среды. В 4 т. Т. 4. Основы механики твердых сред. М.: Изд-во МГТУ им. Н.Э. Баумана, 2013. 620 с.
22. Димитриенко Ю.И. Механика сплошной среды. В 4 т. Т. 2. Универсальные законы механики и электродинамики сплошной среды. М.: Изд-во МГТУ им. Н.Э. Баумана. 2011. 560 с.
23. Димитриенко Ю.И., Соколов А.П. Разработка системы автоматизированного вычисления эффективных упругих характеристик композитов // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2008. № 2. С. 57-67.
24. Димитриенко Ю.И., Соколов А.П. Автоматизация прогнозирования свойств композиционных материалов на основе метода асимптотического осреднения // Информационные технологии. 2008. № 8. С. 31-38.
Публикации с ключевыми словами: моделирование, термоупругость, композиционные материалы, метод асимптотического осреднения, высокие температуры, метод конечного элемента, неорганические связующие, алюмо-хромофосфатные связующие, термомеханика, многоуровневая микроструктура
Публикации со словами: моделирование, термоупругость, композиционные материалы, метод асимптотического осреднения, высокие температуры, метод конечного элемента, неорганические связующие, алюмо-хромофосфатные связующие, термомеханика, многоуровневая микроструктура
Смотри также:
- Моделирование нестационарного внутреннего теломассопереноса в теплозащитных кострукциях на основе трехмерного конечно-элементного анализа
- Оптимизация многокомпонентных дисперсно-армированных композитов на основе сплайн-аппроксимации
- Математическое моделирование диэлектрических свойств полимер-керамических композиционных материалов методом асимптотического осреднения
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



