научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2013
DOI: 10.7463/1013.0623343
УДК 539.8
Россия, МГТУ им. Н.Э. Баумана
Введение
В связи с необходимостью создания изоляционных многокомпонентных гетерогенных систем, обладающих диэлектрическим усилением, возникает вопрос о моделировании эффективных свойств композиционных материалов [9, 10, 12]. Описание воздействия электромагнитного поля на сильно неоднородные среды осуществляется с помощью уравнений с быстроосциллирующими коэффициентами, характеризующими свойства отдельных компонент композиционного материала. Основная идея метода асимптотического осреднения дифференциальных уравнений (МАО), предложенного в работах Н. С. Бахвалова, E. Санчез-Паленсии, А. Бенсуссана [1, 11, 13], состоит в замене гетерогенного материала однородной средой, обладающей усредненными физико-механическими параметрами. Быстроосциллирующие коэффициенты уравнений представляются в виде периодических функций. Проводится асимптотическое исследование решений поставленной задачи. Однако, применимость МАО ограничивается поиском эффективных характеристик композитов, обладающих достаточно простой геометрической структурой. Для расчета эффективных свойств сложноструктурированных композиционных материалов, обладающих свойством центральной симметрии (рис. 1), разработана модернизация МАО приводящая задачу с периодическими граничными условиями к серии задач, так называемых Lp , классического типа [4-8]. Решается цикл обратных задач Lp с адаптированными компонентами в направлениях пространства для установления эффективных характеристик композита и тангенса угла диэлектрических потерь.
Решение серии Lp задач и поиск эффективных характеристик композита
Для композиционного материала, характерный размер которого ![]() , и существует характерный размер ячейки периодичности (ЯП)
, и существует характерный размер ячейки периодичности (ЯП) ![]() введем малый параметр
введем малый параметр  , и два типа безразмерных координат:
, и два типа безразмерных координат:  – глобальные,
– глобальные,  – локальные, где
– локальные, где ![]() – декартовы координаты.
– декартовы координаты.
Исходя из периодичности структуры композита, периодический характер присваивается диэлектрической проницаемости, комплексная амплитуда которой будет рассматриваться как функция координат ![]() :
:![]() , где
, где ![]() – длина сторон ЯП.
– длина сторон ЯП.
Относительно потенциала ![]() строится асимптотического разложения по параметру
строится асимптотического разложения по параметру ![]() :
:
 (1)
(1)
Для объема ЯП  введены фазы
введены фазы ![]() , принадлежащие разному типу компонент. С использованием разложения (1), свойств периодичной функции, правил дифференцирования сложной функции рассмотрим систему уравнений, описывающую воздействие переменного электрического поля на композит
, принадлежащие разному типу компонент. С использованием разложения (1), свойств периодичной функции, правил дифференцирования сложной функции рассмотрим систему уравнений, описывающую воздействие переменного электрического поля на композит
 (2),
(2),
где ![]() – операция осреднения по «ячейке периодичности»,
– операция осреднения по «ячейке периодичности», ![]() -условия периодичности,
-условия периодичности, ![]() -средняя напряженность композита.
-средняя напряженность композита.
Задача (2) содержит нестандартные условия нормировки в виде интегральных уравнений Вольтера первого рода и условия периодичности на границе ЯП, что создает трудности при численном ее решении. Для упрощения поиска решения вводим функции псевдопотенциала
 , (3)
, (3)
где![]() ;
; ![]() – новые неизвестные функции от
– новые неизвестные функции от ![]() , уже не являющиеся периодическими.
, уже не являющиеся периодическими.
Далее вводится предположение о центральной симметрии ЯП относительно центра локальных координат, что позволяет вместо решения на всей ЯП ![]() решение на 1/8 ЯП
решение на 1/8 ЯП ![]() .
.
Используя выражения (4) получаем задачу электродинамики композита на 1/8 ЯП
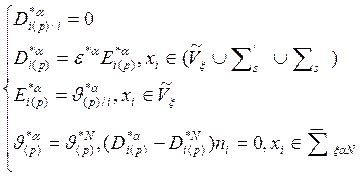 , (4)
, (4)
где  - поверхности контакта компонентов внутри подобласти, координатные плоскости –
- поверхности контакта компонентов внутри подобласти, координатные плоскости –![]() , торцевые поверхности «ячейки периодичности»–
, торцевые поверхности «ячейки периодичности»– ![]()
К задаче (4) присоединяются граничные условия на 1/8 ЯП
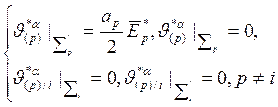 . (5)
. (5)
Задачи Lp имеют «классический» вид относительно функций ![]() , т.е. являются «контактными» задачами электростатики с граничными условиями на поверхности области
, т.е. являются «контактными» задачами электростатики с граничными условиями на поверхности области ![]() .
.
Компоненты тензора эффективной комплексной диэлектрической проницаемости среды определяется как
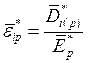 ,
,
где  -осредненная по объему ЯП индукция электрического поля.
-осредненная по объему ЯП индукция электрического поля.
Метод конечных элементов для серии Lpзадач
На объеме 1/8 ЯП, аналогично работе [5], рассмотрим вариационную формулировку задачи электродинамики
 , (6)
, (6)
где ![]() - комплексная амплитуда вектора индукции внешнего поля, заданного на поверхности «ячейки периодичности» композита
- комплексная амплитуда вектора индукции внешнего поля, заданного на поверхности «ячейки периодичности» композита ![]() , на поверхности
, на поверхности ![]() – нулевые граничные условия;
– нулевые граничные условия; ![]() и
и ![]() - виртуальное изменение псевдопотенциала и производная виртуального изменения.
- виртуальное изменение псевдопотенциала и производная виртуального изменения.
Для решения вариационного уравнения (6) используется метод конечных элементов. Область ![]() разбивается на четырехузловые элементы
разбивается на четырехузловые элементы ![]() :
: ![]() . Для каждого элемента
. Для каждого элемента ![]() записывается уравнение (6) имеет вид
записывается уравнение (6) имеет вид
 (7)
(7)
Псевдопотенциал ![]() аппроксимируем как
аппроксимируем как
![]() , (8)
, (8)
где ![]() –координатный столбец значений электрического потенциала
–координатный столбец значений электрического потенциала ![]() в узлах конечного элемента,
в узлах конечного элемента, ![]() – координата j-го узла конечного элемента, j=1…m, m– число узлов,
– координата j-го узла конечного элемента, j=1…m, m– число узлов, ![]() – матрица функций формы.
– матрица функций формы.
Производные от псевдопотенциала ![]() представим в виде координатного столбца
представим в виде координатного столбца
![]() , (9)
, (9)
где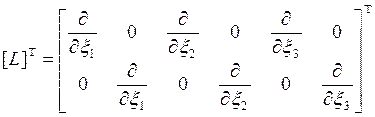 – матрица операторов дифференцирования.
– матрица операторов дифференцирования.
Вариационное уравнение (7) с учетом (8) и (9) имеет вид

где ![]() – матрица градиентов потенциала. Вынося вариацию
– матрица градиентов потенциала. Вынося вариацию ![]() за знак интегралов, получаем разрешающую систему линейных алгебраических уравнений (СЛАУ):
за знак интегралов, получаем разрешающую систему линейных алгебраических уравнений (СЛАУ):
![]() . (10)
. (10)
В СЛАУ (10) матрица ![]() является локальной матрицей «жесткости» для конечного элемента, представленной выражением:
является локальной матрицей «жесткости» для конечного элемента, представленной выражением:
 ,
,
где тензор диэлектрической проницаемости ![]() .
.
Локальный вектор правой части![]() СЛАУ (10) имеет вид
СЛАУ (10) имеет вид
 .
.
Таким образом, если собрать СЛАУ (10) для всех конечных элементов, то получим глобальную СЛАУ относительно псевдопотенциала для всей рассматриваемой области ![]()
![]() , (3.34)
, (3.34)
где ![]() – глобальная матрица жесткости,
– глобальная матрица жесткости, ![]() – глобальный столбец внешних нагрузок. Решением (3.34) получаем распределение электрического поля внутри проектируемого наноструктурированного композита.
– глобальный столбец внешних нагрузок. Решением (3.34) получаем распределение электрического поля внутри проектируемого наноструктурированного композита.
Численный расчет эффективных диэлектрических характеристик
В качестве исследуемого образца выбран композит на основе поливинилхлорида (ПВХ) - матрица и сегнетоэлектрической керамики ЦТС-19 - наполнитель. Для определения диэлектрических свойств композита при воздействии переменного электромагнитного поля проведен расчет серии Lpзадач с применением метода конечных элементов и метода бисопряженных градиентов, на базе программного комплекса, разработанного в НОЦ «СИМПЛЕКС» МГТУ имени Н.Э. Баумана.
Для двух типов геометрий композиционных материалов – с ячейкой периодичности (ЯП) гексагонального типа с различными радиусами армирующих включений (рис. 1), рассчитана эффективная диэлектрическая проницаемость при воздействии электрического поля диапазона частот от 10-2 до104 Гц. Установлена частотная зависимость мнимой и действительной части комплексной диэлектрической проницаемости композитов на основе пластиката для мелкодисперсного наполнителя ЦТС-19 характерными размерами ~1 мкм и ~10 мкм при равной объемной доле включений (рис. 2 и рис. 3).

Рис. 1. Композиционный материал с мелкодисперсным наполнителем 2-х типов: с гексагональной формой ЯП и с кубической симметрией ЯП
Оценка адекватности математической модели и точности численных методов расчета эффективных диэлектрических характеристик получены посредством сравнения расчетных характеристик действительной и мнимой частей ![]() и
и ![]() эффективной диэлектрической проницаемости, а также тангенса угла диэлектрических потерь
эффективной диэлектрической проницаемости, а также тангенса угла диэлектрических потерь ![]() композита с результатами экспериментальных данных [2, 3].
композита с результатами экспериментальных данных [2, 3].

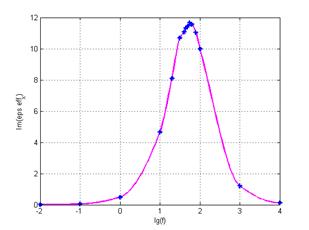
Рис. 2. Частотные зависимости ε' и ε̋ для композита на основе ПВХ с керамическими включениями ЦТС-19, d~1 мкм, φf=40%

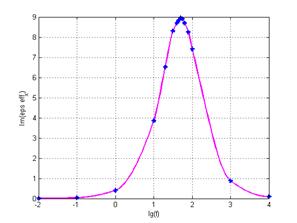
Рис. 3. Частотные зависимости ε' и ε̋ композита на основе ПВХ с керамическими включениями ЦТС-19, d~10мкм, φf=40%
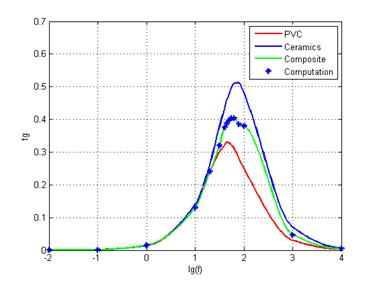
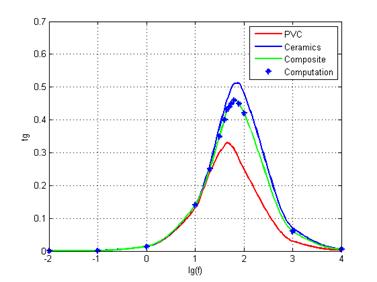
Проведен расчет тангенса угла диэлектрических потерь для каждого типа композита с коэффициентами армирования φf равными 10% и 40 %, что позволяет проанализировать энергоемкость композита и в дальнейшем установить оптимальную концентрацию керамических включений в композите (рис. 4-5). Характер поведения тангенса угла диэлектрических потерь, при варьировании объемной доли включений, свидетельствует о хорошей точности используемых математических методов и соответствии физическому смыслу математической модели.

а) б)
Рис. 4. Расчетные и экспериментальные зависимости тангенс угла диэлектрических потерь tgδ компонентов композита: (ПВХ –PVC), керамики ЦТС-19 и самого композита, φf=10% , d~10 мкм (а), d~1 мкм (б)
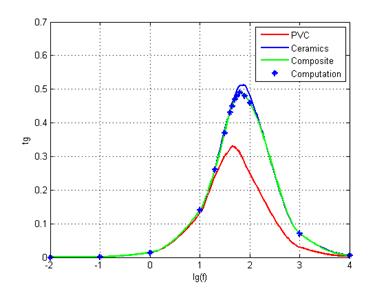
а) б)
Рис. 5. Расчетные и экспериментальные зависимости тангенс угла диэлектрических потерь tgδ компонентов композита: (ПВХ –PVC), керамики ЦТС-19 и самого композита, φf=40% , d~10 мкм (а), d~1 мкм (б) .
Заключение
В данной работе проведено асимптотическое исследование эффективных диэлектрических характеристик сложноструктурированных композитов с применением МАО. Сформулирована серия локальных задач на «ячейке периодичности» композита. Проведен расчет эффективной диэлектрической проницаемости полимерного композита с мелкодисперсными включениями керамики ЦТС-19 с применением метода конечных элементов. Проанализирована частотная зависимость диэлектрических характеристик и тангенса угла диэлектрических потерь гетерогенных структур с различными концентрациями и размерами мелкодисперсных включений при воздействии электрического поля в диапазоне частот от 10-2 до104 Гц. Получено хорошее совпадение численных расчетов и экспериментальных данных для диэлектрических свойств дисперсно-армированных полимер-керамических композитов[2, 3].
Поддержка
Работа проведена при финансовой поддержке Министерства образования и науки Российской Федерации по Соглашениям о предоставлении гранта в форме субсидий № 14.B37.21.0448, 14.B37.21.1869, НИР № 1.5433.2011, № 14.132.21.1699 в рамках ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 годы и РФФИ № 12-08-00998.
Список литературы
1. Бахвалов Н.С., Панасенко Г.П. Осреднение процессов в периодических средах. Математические задачи механики композиционных материалов. М.: Наука, 1984. 352 с.
2. Гефле О.С., Лебедев С.М., Похолков Ю.П. Частотные спектры комплексной диэлектрической проницаемости композиционных диэлектриков на основе поливинилхлорида // Известия Томского политехнического университета. 2007. Т. 310, № 1. С. 87-91.
3. Гефле О.С., Лебедев С.М., Ткаченко С.Н. Поведение полимерных композиционных материалов с наполнителем из сегнетоэлектрической керамики в электрическом поле // Известия Томского политехнического университета. 2005. Т. 308, № 4. С. 64-68.
4. Димитриенко Ю.И., Кашкаров А.И. Расчет эффективных характеристик композитов с периодической структурой методом конечных элементов // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2002. № 2. С. 95-108.
5. Димитриенко Ю.И., Соколов А.П. Многомасштабное моделирование упругих композиционных материалов // Математическое моделирование. 2012. Т. 24, № 5. С. 3-20.
6. Димитриенко Ю.И., Соколов А.П. Разработка системы автоматизированного вычисления эффективных упругих характеристик композитов // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2008. № 2. С. 57-67.
7. Димитриенко Ю.И., Соколов А.П. Система автоматизированного прогнозирования свойств композиционных материалов // Информационные технологии. 2008. № 8. С. 31-38.
8. Димитриенко Ю.И., Соколов А.П., Маркевич М.Н. Моделирование диэлектрических характеристик композиционных материалов на основе метода асимптотического осреднения // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2013. № 1.
DOI: 10.7463/0113.0531682
9. Емец Ю.П. Эффективная диэлектрическая проницаемость трехкомпонентных композиционных материалов с анизотропной структурой // Журнал технической физики. 2005. Т. 75, вып. 2. С. 67-72.
10. Шелухин В.В., Терентьев С.А. Гомогенизация уравнений Максвелла и дисперсия Максвелла-Вагнера // Доклады Академии наук. 2009. Т. 424, № 3. С. 402-406.
11. Bensoussan A., Lions JL., Papanicalaou G Asymptotic analysis for periodic structures. Amsterdam; New York: North-Holland Pub. Co.,1978. 396 p.
12. Kettunen H., Qi J., Wallen H., Sihvola A. Frequency dependence of effective permittivity of simple dielectric composites // Proceedings of ACES 2010. Tampere, Finland. 2010. P. 248-253.
13. Sanchez-Palencia E. Book chapters // In: Homogenization techniques for composite media /Sanchez-Palencia E., Zaoui A. (eds.). Berlin, Heidelberg: Springer, 1987. P. 121-192. DOI: 10.1007/3-540-17616-0 (Ser. Lecture notes in Physics; no. 272).
Публикации с ключевыми словами: математическое моделирование, композиционные материалы, метод асимптотического осреднения, эффективная диэлектрическая проницаемость, сегнетоэлектрическая керамика
Публикации со словами: математическое моделирование, композиционные материалы, метод асимптотического осреднения, эффективная диэлектрическая проницаемость, сегнетоэлектрическая керамика
Смотри также:
- Метод решения задачи оптимизации структуры дисперсно-армированных композитов при ограничениях на тепловые и прочностные свойства
- Моделирование термоупругих характеристик композитов на основе алюмо-хромофосфатных связующих
- Моделирование высокоскоростных процессов в демпфирующих системах с фазовыми превращениями
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



