научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 09, сентябрь 2013
DOI: 10.7463/0913.0623173
УДК 537.876
Россия, МГТУ им. Н.Э. Баумана
Россия, Москва, ФГУП «ЦНИРТИ им. академика А.И. Берга»
Введение
Объектом исследования является взаимодействие дисперсной системы с электромагнитным излучением (ЭМИз) сверхвысокочастотного (СВЧ) диапазона. В широком смысле слова, дисперсная система – смесь из двух и более веществ, которые не реагируют друг с другом химически. Из них наибольший интерес для исследования представляют аэрозоли – дисперсные системы, в которых дисперсионной средой является газ, а дисперсной фазой – твердые или жидкие частицы [1]. Они могут быть как естественного (пыль, туман, дым), так и искусственного происхождения. Под искусственно созданными дисперсными системами будем понимать взвесь из специально созданных частиц с особыми свойствами. Такие дисперсные системы актуальны в связи с их применением для изменения условий распространения ЭМИз СВЧ в пространстве; т.е. такие дисперсные системы могут применяться как аэрозольные образования для уменьшения радиолокационной (РЛ) заметности на СВЧ объектов военной техники (наземной, воздушной, космической) при условии, что такие дисперсные системы поглощают ЭМИз СВЧ без существенного отражения ЭМИз СВЧ. Таким образом, в настоящее время актуальной является задача разработки дисперсной системы, не отражающей, но поглощающей ЭМИз СВЧ. В представляемой работе авторы предлагают методику расчета слабо отражающей, но поглощающей ЭМИз СВЧ дисперсной системы, связывающую параметры дисперсной системы (концентрацию, геометрическую форму и размеры частиц, диэлектрическую и магнитную проницаемость материала частиц) с ее радиопоглощательными и радиоотражательными характеристиками. В данной работе рассматривается дисперсная среда, состоящая из взвеси нитевидных структур в воздухе. Нитевидные структуры представляют собой вытянутые частицы, имеющие большое отношение длины к диаметру. Обоснование использования частиц именно такой формы приводится ниже.
Известна теоретическая модель дисперсной системы (аэрозольного образования) для расчета ее радиопоглощательных и радиоотражательных характеристик [2–4]. В данной модели рассматривается дисперсная система из вытянутых эллипсоидов, выполненных из диэлектрического материала и покрытых слоем из электропроводного материала. Радиопоглощательные и радиоотражательные характеристики такой системы оцениваются с помощью понятий эффективной диэлектрической проницаемости εeff и эффективной проводимости σeff системы:
![]()
![]() , (1)
, (1)
где ε – диэлектрическая проницаемость материала эллипсоидов, µ – масса эллипсоидов в единичном объеме системы, µ0 – плотность материала эллипсоидов (таким образом, µ/µ0 – объемная доля эллипсоидов в рассматриваемом объеме), σ и m0 – проводимость и плотность электропроводного материала, m – масса электропроводного материала в единичном объеме. Такой подход весьма спорен, поскольку формулы (1) представляют собой достаточно грубую оценку и не являются общепринятыми. В настоящей работе авторы предприняли попытку сформулировать альтернативные соотношения (составляющие методику расчета слабо отражающей, но поглощающей ЭМИз СВЧ дисперсной системы). Вывод альтернативных соотношений основывался на следующих соображениях.
Проходя через дисперсную систему, часть электромагнитных волн (ЭМВ) отражается (рассеивается) и поглощается, а часть проходит насквозь. Соответственно, для среды (дисперсной системы) можно ввести взаимосвязанные между собой коэффициенты прохождения, отражения и поглощения (для полного описания достаточно рассчитать любые два из этих коэффициентов; мы будем рассчитывать коэффициенты отражения и поглощения). Как известно, свойства среды описывают материальные уравнения [5], устанавливающие связь между векторами напряженности электрического и магнитного поля и векторами электрической и магнитной индукции в среде:
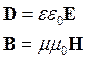 , (2)
, (2)
где
E – вектор напряжённости электрического поля,
H – вектор напряжённости магнитного поля,
D – вектор электрической индукции,
B – вектор магнитной индукции,
ε, μ – диэлектрическая и магнитная проницаемости вещества,
ε0, μ0 – константы системы СИ.
Таким образом, достаточно знать диэлектрическую и магнитную проницаемости среды, чтобы понять, какими будут коэффициенты отражения, поглощения и прохождения. Для немагнитных веществ μ = 1 (рассмотрим этот случай), и можно ограничиться нахождением одной лишь диэлектрической проницаемости ε.
Метод расчёта отражательных и поглощательных характеристик системы
Соотношения (2) справедливы для сплошных сред. Но можно ли считать дисперсную систему сплошной средой? Очевидно, что это зависит от конкретных значений длины волны падающего ЭМИз, размера и концентрации частиц дисперсной фазы. Для дисперсной системы с заданными параметрами, весь диапазон ЭМИз может быть условно разделен на три области (поддиапазона):
1) Длина волны падающего ЭМИз много больше размеров частиц дисперсной фазы и расстояния между ними;
2) длина волны падающего ЭМИз больше размеров частиц, но меньше расстояния между ними;
3) длина волны падающего ЭМИз меньше размеров частиц.
В данной работе рассматривается первая область спектра. В первой области спектра корректно применение приближения геометрической оптики: дисперсную систему можно рассматривать как прозрачную сплошную среду с некоторой эффективной диэлектрической проницаемостью εэфф (как это и было сделано в [4]). Однако, для расчета εэфф дисперсной системы авторы предлагают вместо грубых соотношений (1) использовать известную формулу Клаузиуса — Моссотти[6] (формула Клаузиуса-Мосотти применима для описания диэлектриков с электронной поляризуемостью, для учета ориентационной поляризуемости, необходимо использовать формулу Ланжевена — Дебая), связывающую эффективную статическую диэлектрическую проницаемость εэфф дисперсной системы с поляризуемостью частиц:
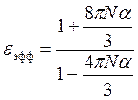 , (3)
, (3)
где
N – концентрация частиц дисперсной фазы,
α – поляризуемость частиц.
Выражение для поляризуемости 𝛼 частицы эллиптической формы с полуосями a, b, c приведено в [7]:
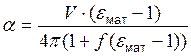 , (4)
, (4)
где
V – объем эллипса,
εмат – диэлектрическая проницаемость материала эллипса,
f – фактор формы.
Фактор формы f, в свою очередь, определяется выражением [7]:
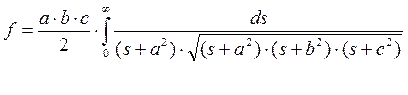 . (5)
. (5)
Конечно, необходимо обозначить границы применимости соотношения Клаузиуса — Моссотти для статических полей в случае переменного поля. Сделаем это по аналогии с [5, С. 153]: если время t распространения ЭМИз от любой точки дисперсной системы до точки наблюдения пренебрежимо мало, статическое приближение вполне приемлемо для описания процессов переменного поля. На практике указанное условие выполняется практически всегда (t=Р/c, где с – скорость света, Р – расстояние между точкой дисперсной системы и точкой наблюдения, имеющее порядок 100 м), таким образом, соотношение Клаузиуса — Моссотти вполне применимо в данной работе. Также необходимо отметить, что в переменных полях диэлектрическая проницаемость среды – комплексная величина, представляемая в виде [5]:
![]() . (6)
. (6)
В классической электродинамике ε'' материала выражается через проводимость материала и частоту падающего ЭМИз [5], [6]:
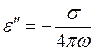 , (7)
, (7)
где
σ – проводимость материала (здесь можно пренебречь вкладом проводимости воздуха, т.к. она намного меньше проводимости материала),
ω– частота падающего ЭМИз.
Подставив (4) в (3), с учетом (5), (6), (7) получим искомую эффективную диэлектрическую проницаемость εэфф дисперсной системы.
Конечным результатом представляемой методики является расчет коэффициента отражения R дисперсной системы по формуле геометрической оптики (аналогично [4]):
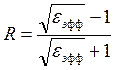 . (8)
. (8)
Затухание ЭМВ в дисперсной системе определяется, подобно сплошной среде, по формуле Бугера — Ламберта — Бера [6]:
![]() , (9)
, (9)
где
I0 – интенсивность падающей волны,
γ – коэффициент затухания дисперсной системы,
z – толщина поглощающего слоя дисперсной системы.
Коэффициент затухания γ, в свою очередь, выражается через найденную диэлектрическую проницаемость εэфф дисперсной системы [6]:
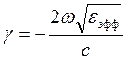 , (10)
, (10)
где
ω – частота ЭМИз,
с – скорость света.
Выражения (9), (10) являются продуктом строгого теоретического расчета для среды с диэлектрической проницаемостью εэфф. Таким образом, вычислив по приведенной методике коэффициент отражения R и коэффициент поглощения A=I/I0, инженер однозначно описывает свойства дисперсной системы в диапазоне длин волн ЭМИз, который был определен как «первый».
Результаты моделирования
Используя приведенную методику, для первой области спектра авторами был произведен расчет параметров дисперсной системы с приемлемыми уровнями отражения и поглощения ЭМИз СВЧ. Данный расчет был основан на следующих исходных данных. Дисперсная система моделировалась как облако частиц (эллипсоидов), имевшее форму полусферы, в центре которой находился защищаемый объект (для которого было необходимо уменьшить РЛ заметность, рис. 1).
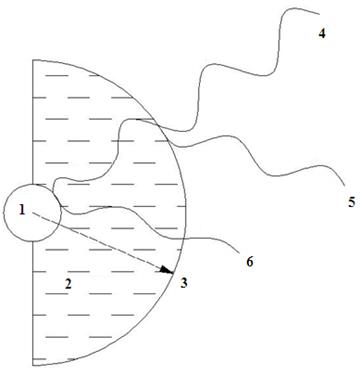
1 – защищаемый объект, 2 – дисперсная система, 3 – толщина защищаемого слоя, 4 – падающий сигнал, 5 – отраженный сигнал, 6 – ослабленный сигнал, отраженный от объекта
Рисунок 1 – Способ снижения заметности объекта в РЛ диапазоне с помощью дисперсной системы
При моделировании полагалось, что коэффициент отражения R дисперсной системы не должен был превышать 0,01, а амплитуда отраженного от объекта сигнала после прохождения дисперсной системы уменьшалась в 10 раз (что соответствовало бы уменьшению мощности этого сигнала на 20 дБ). То есть результирующий отраженный сигнал (сумма отраженного от дисперсной системы и объекта сигналов) должен был испытывать ослабление по сравнению с падающим сигналом на 20 дБ. В результате расчета были получены параметры дисперсной системы (удовлетворявшей указанным требованиям по коэффициенту отражения): радиус полусферы, концентрация частиц, масса дисперсной системы*, частотный диапазон ЭМИз и др. (таблица 1, 2). В таблице 1 приведены полученные параметры частиц дисперсной фазы. Расчет показал, что частицы вытянутой формы, имеющие отношение длины к диаметру порядка 500 (таблица 1), обеспечивают выполнение указанных требований по коэффициенту отражения при концентрации более низкой, чем в случае, например, частиц сферической и прочей непродолговатой формы. В таблице 2 приведены остальные параметры дисперсной системы, удовлетворявшей заявленным требованиям по коэффициенту отражения. Нижние границы частотных диапазонов ЭМИз из таблицы 2 соответствовали максимальному отражению ЭМИз от дисперсной системы и минимальному поглощению ЭМИз (наихудший случай). С увеличением частоты ЭМИз коэффициент отражения R дисперсной системы уменьшался, а уровень поглощения ЭМИз увеличивался. Верхние границы диапазонов из таблицы 2 соответствовали минимальному отражению ЭМИз от дисперсной системы и максимальному поглощению ЭМИз (наилучший случай). Верхние границы диапазонов определялись минимальными длинами волн, для которых теоретическая модель представленной методики сохраняла физический смысл (для соответствующих значений концентрации частиц).
Таблица 1 - Расчетные параметры частиц дисперсной фазы
Малая полуось эллипса (ось а = ось b), мкм | Большая полуось эллипса (ось c), мкм | Проводимость, | Относительная диэлектрическая проницаемость (стат. значение) |
2,4
| 1000 | 104 | от 1 до 10 |
Результаты, представленные в таблице 2, отражают один из вариантов практического применения таких дисперсных систем – снижение заметности объекта в радиолокационном диапазоне частот.
Таблица 2 - Расчетные параметры дисперсной системы при ее практическом применении для снижения заметности объекта в радиолокационной области
Радиус полусферы, м | Масса дисперсной системы, кг | Концентрация частиц N, м-3 | Диапазон работы Δf, ГГц |
14,517 | 0,6180 | 107 | от 2,725 (11 см) до 64,6 (4,6 мм) |
3,149 | 0,0063 | 107 | от 12 (2,5 см) до 64,6 (4,6 мм) |
14,200 | 3,7050 | 6,4·107 | от 1 (30 см) до 120 (2,5 мм) |
Заключение
Таким образом, представлена методика расчета слабо отражающей, но поглощающей ЭМИз СВЧ дисперсной системы. В представленной методике использованы более строгие соотношения, чем, например в [4]. Она показала возможность создания дисперсной системы, функционирующей в диапазоне частот от 1 ГГц (30 см) до 120 ГГц (2,5 мм). При этом ее размеры (14 м) сравнимы с размерами объекта военной техники, а масса дисперсной фазы составляет всего 3,7 кг. Конечно, заявленная методика нуждается в экспериментальном подтверждении. Используя полученную методику, задавшись широким диапазоном значений исходных параметров (a, b, c, εмат, N) определить наилучшие значения этих параметров, соответствующие минимальному коэффициенту отражения R и максимальному коэффициенту затухания γ дисперсной системы в как можно более широком диапазоне Δf.
Работа выполнена при финансовой поддержке в рамках государственного контракта № 14.513.11.0025 ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы».
7. Список литературы
1. Фукс Н.А. Механики аэрозолей. М.: Издательство Академии наук СССР, 1955. 351 с.
2. Алексашенко В.А., Соловьев А.А. Обоснование возможности изменения параметров среды прохождения электромагнитных сигналов в широком диапазоне частот // VIII международная конференция « Кибернетика и высокие технологии XXI века» (C&T-2007) (Воронеж, ВГУ, 15–17 мая 2007 г.) : тр. Воронеж, 2007.
3. Алексашенко В.А., Соловьев А.А., Солодов А.А. Создание поглощающих сред // Вестник АВН. 2008. № 4.
4. Алексашенко В.А., Кузина М.Ю., Лобанов Б.С. Разработка теоретической модели и технологии создания искусственных сред, поглощающих электромагнитные излучения в широком диапазоне частот – от радиолокационного до оптического // 15 международная научно-техническая конференция «Радиолокация, навигация, связь» : тр. Воронеж, 2009.
5. Никольский В.В. Теория электромагнитного поля. М.: Высшая школа, 1961. 372 с.
6. Петров Ю.И. Физика малых частиц. М.: Наука, 1982. 327 с.
7. Хиппель А. Р. Диэлектрики и их применение: пер. с англ. М.: Госэнергоиздат, 1959. 335 с.
Публикации с ключевыми словами: моделирование, поглощение, рассеяние, электромагнитная волна, СВЧ диапазон, дисперсная среда
Публикации со словами: моделирование, поглощение, рассеяние, электромагнитная волна, СВЧ диапазон, дисперсная среда
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



