научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 05, май 2012
УДК 621.3
Россия, МГТУ им. Н.Э. Баумана
Россия, Южный федеральный университет
В современных сверхбольших интегральных схемах (далее СБИС) с субмикронными размерами элементов используется многослойная металлизация, применение которой позволяет существенно повысить степень интеграции, поскольку в этом случае всю поверхность кристалла можно использовать для формирования только активных структур [1]. Однако ее применение, как, впрочем, и применение любой другой технологии, создает и свои проблемы. Одной из таких проблем является возникновение рельефа на поверхности кристалла при формировании нескольких проводящих слоев, что приводит к технологическим трудностям при их создании.
Известно, что для формирования слоя межсоединений при производстве КМОП СБИС используют субтрактивный процесс. Это значит, что первоначально на поверхность пластины наносят сплошной проводящий слой, в котором с помощью операций литографии и последующего травления открытых участков получают требуемый рисунок межсоединений.
После получения рисунка проводящего слоя на него осаждают изолирующий слой (обычно изолятором является диоксид кремния), причем в процессе осаждения над проводниками образуются локальные ступеньки (рельеф). Если не принять соответствующих мер, то в таком случае формирование следующего проводящего слоя будет осуществляться уже на рельефную поверхность, что может привести к разрывам участков проводников, имеющих малую толщину. Кроме того, вследствие более низкой скорости травления проводящего слоя на наклонных участках могут остаться непротравленные области. В этом случае наличие рельефа может привести и к возникновению закороток.
Для удаления локальной ступеньки, возникающей при осаждении диоксида кремния, используют технологический процесс химико-механической планаризации (далее ХМП), в силу особенностей которого, на поверхности кристалла СБИС тем не менее возможно сохранение рельефа поверхности (глобальной ступеньки).
Одной из проблем связанных с возникновением глобальной ступеньки на поверхности пластины является ограничение процесса получения резистивной маски при проекционной литографии. Известно [2], что в соответствии со вторым критерием Релея, глубина фокусировки DOF оптической системы установки проекционной литографии определяется выражением:
 ,
,
где λ – длина волны экспонирующего излучения, а NA – числовая апертура объектива. Это значит, что в случае использования, например, установки проекционной литографии с параметрами: λ = 365 нм, NA = 0,6, глубина фокусировки составит величину порядка 0,5 мкм. Дополнительно при наличии рельефа поверхности пластины в процессе изготовления СБИС возможно наличие непротравленных контактных окон, а при увеличении времени травления - их растравливание.
Всё вместе сказанное приводит к нестабильности технологического процесса производства СБИС и снижению процента выхода годных микросхем.
Описанную технологию формирования многоуровневой металлизации обычно применяют для производства СБИС с минимальной проектной нормой большей 0,13 мкм. При меньшей проектной норме в качестве материала для формирования многослойной металлизации вместо алюминия используют медь. В этом случае при получении рисунка проводящего слоя возникают сложности с ее эффективным травлением. С целью решения данной проблемы фирмой “IBM” разработана технология dual-damascene process, в которой ХМП проводится по слою меди, а не диоксида [3].
Особенности технологического процесса ХМП
Хотя процесс ХМП и позволяет повысить планарность слоя двуокиси кремния, но технологически он имеет и свои определенные недостатки.
В результате исследований, проведенных группой специалистов из Массачусетского Технологического Института (МТИ), в которых использовались четыре тестовых фотошаблона (ФШ), было показано, что ключевым параметром, который влияет на процесс планаризации диоксида кремния, является плотность заполнения нижележащего слоя [1].

Рис. 1. Тестовые ФШ, использованные специалистами МТИ для исследования характеристик процесса ХМП, и полученные с их помощью результаты
Вид тестовых ФШ и результаты проведенных с их помощью исследований иллюстрирует рисунок 1. Из графиков видно, что для ФШ с изменяющимися площадью, шагом и отношением периметра к площади при планаризации диоксида выраженных зависимостей нет. Тогда как для шаблона с изменяющейся плотностью хорошо видна линейная зависимость конечной толщины диоксида (толщина, отсчитываемая от верхней точки слоя металлизации) от плотности заполнения нижележащего слоя.
В результате анализа полученных данных становится очевидным, что процесс ХМП наиболее чувствителен к плотности заполнения рисунка проводящего слоя, на который наносится изолирующий слой диоксида кремния. Это следует и из того, что осаждение изолирующего окисла проводится по технологии осаждения из газовой фазы (CVD, Chemical-VaporDeposition), в которой диоксид осаждается конформно, то есть, повторяя нижележащий рельеф поверхности кристалла СБИС с некоторым уширением проводников. Следовательно, плотность заполнения нижележащего слоя передается изолирующему диоксиду, но при этом необходимо учитывать уширение проводников.
Задача моделирования процесса ХМП связана с задачей получения оптимального заполнения топологического слоя фиктивными фигурами (далее dummy-структуры). С помощью dummy-структур существует возможность заполнить пустые места топологии таким образом, чтобы получить наименьший разброс плотности заполнения рисунка топологического слоя по кристаллу, что, в свою очередь, приведет к снижению разброса толщины межслойного диэлектрика.
Локальная и эффективная плотность заполнения
Для вычисления локальной плотности заполнения слоя d разделим весь топологический слой на квадраты со стороной W так, как показано на рисунке 2. Тогда после разбиения будем иметь одинаковую для всех квадратов площадь, равную Sкв = W2, и суммарную площадь элементов, которые лежат внутри квадрата, равную Sэл. Локальную плотность заполнения квадрата i,j определим как: dij = Sij эл/Sкв.

Рис. 2. Вычисление локальной плотности заполнения топологического слоя
Чтобы непосредственно осуществить моделирование процесса ХМП, необходим расчет эффективной плотности заполнения, являющейся результатом двумерной свертки локальной плотности заполнения d и некоторой матрицы, называемой ядром свертки. Последнее определяет «величину» влияния между соседними элементами топологии (локальной плотности) и расстояние, на котором его необходимо учитывать. С точки зрения физической интерпретации ядро свертки позволяет учесть прогиб полировальной подушки и степень ее адаптации к рельефу поверхности.
Двумерная свертка рассчитывается по следующему выражению:
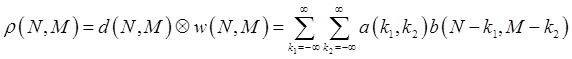
где d(N,M) – матрица локальной плотности заполнения исходной топологии, а w(N,M) – ядро свертки.
Задача расчета локальной плотности заполнения
На первый взгляд данная задача является тривиальной. Заметим, что она относится к области вычислительной геометрии, которая как раз и рассматривает алгоритмы решения геометрических задач автоматизированными средствами [4, 5].
Таким образом, задача расчета локальной плотности заполнения сводится к пересечению N не перекрывающихся одинаковых квадратов заданного размера и расположенных без зазора по всей площади кристалла с содержимым топологического слоя СБИС, представленного в виде множества произвольных не перекрывающихся полигонов, то есть к выполнению логической операции дизъюнкции. После ее выполнения необходимо вычислить площадь отсеченных полигонов, лежащих внутри обрабатываемого квадрата. В результате работы всего алгоритма должен быть получен двумерный массив вещественных значений. Элементы данного массива содержат значения площади отсеченных полигонов для каждого из квадратов. Для получения же матрицы локальной плотности заполнения каждый из элементов этого массива необходимо разделить на площадь квадрата.
Если принять во внимание то обстоятельство, что рабочие элементы топологии не перекрываются и не накладываются друг на друга и весь топологический слой представляет собой K многоугольников (далее полигонов), то вычислительная сложность алгоритма в операциях пересечения двух полигонов равна R = Θ(N×K).
Рассмотрим следующий пример. Пусть число полигонов в топологическом слое металлизации с проектной нормой 0,35 мкм равно 5×106 и они размещены на квадратном кристалле площадью S = 10 мм2. Тогда для расчета локальной плотности заполнения число квадратов со стороной 80 мкм (размер сетки моделирования, см. [1]), составит:
В результате имеем следующее число пересечений полигонов с квадратами расчета локальной плотности:
![]()
Отметим что на практике, расчет локальной плотности заполнения с использованием различных библиотек вычислительной геометрии, таких как KBool, CGAL, GGL, PolyBoolean и GPC для реального кристалла СБИС оказался невозможным. Выяснение причин этого показало, что библиотеки CGAL, CGL, GPC эффективно обрабатывают графическую информацию и плохо – топологическую информацию большого объема, а библиотеки KBool и PolyBoolean требуют больших затрат оперативной памяти для хранения информации о полигонах топологического слоя перед его обработкой.
Кроме того, недостаток большинства приведенных библиотек применительно к обработке топологии слоев СБИС, представленных в формате GDSII, состоит в том, что эти библиотеки работают с полигонами, в которых отверстия представляются отдельными контурами. В результате возникают дополнительные вычислительные затраты, связанные с проверкой существования в полигоне отверстий и, при положительном результате, в необходимости определения внешнего и внутреннего контуров.
В настоящее время существует система автоматизированного проектирования (далее САПР) Calibre компании “MentorGraphics”, которая позволяет проводить расчет локальной плотности заполнения с учетом указанных выше требований. Однако данная САПР является закрытой, что не позволяет напрямую использовать ее возможности при решении задач, требующих разработки дополнительного программного обеспечения (далее ПО).
Тем не менее, для решения задачи оптимального заполнения топологического слоя dummy-структурами необходимо иметь возможность проводить соответствующие расчеты, используя только одну систему. Поэтому весь алгоритм заполнения должен быть реализован как единая программа, что невозможно при использовании вышеуказанной САПР.
Представление полигона
Для решения задачи оптимального заполнения топологического слоя СБИС dummy-структурами был разработан алгоритм расчета локальной плотности заполнения, использующий послойную топологическую информацию, представленную в виде набора полигонов, в котором сами полигоны, в свою очередь, представлены в виде набора точек – вершин полигона.
Вершины полигона соединены ребрами. Причем нормальным считается обход вершин полигона против часовой стрелки. Тогда расчет его площади дает положительное значение, необходимое для вычисления локальной плотности. Однако в этом случае необходимо учитывать и направление обхода полигона при вычислении его пересечения с квадратом. Представление полигона согласно приведенному выше правилу показано на рисунке 3.

Рис. 3. Представление полигона
Информационно полигон представляется в виде одномерного массива целых 32-х битных координат. При выполнении операции пересечения полигона с квадратом расчета локальной плотности заполнения массив его координат переписывается в список. Хранение координат в виде списка позволяет повысить быстродействие алгоритма нахождения пересечения в случае добавления и исключения элементов (координат вершин), тогда как постоянное хранение информации обо всех координатах полигонов в виде списков требует больших затрат оперативной памяти.
Для сохранения информации о каждом из полигонов требуется хранить все его координаты (два 32-х битных числа), число вершин (32-х битное значение) и указатель на область памяти (64-х битное значение). То есть общее число бит информации для хранения одного полигона в этом случае будет равно 64N+96, где N – число вершин полигона. Тогда как в двусвязном списке кроме координат полигона и числа его вершин к каждой координате необходимо добавить еще два указателя (два 64-х битных значения). Общий объем затрачиваемой памяти в этом случае составит 128N+32 бит.
Алгоритм «разбиения» слоя
В приведенном выше примере для расчета локальной плотности заполнения большое число операций пересечения вызвано тем, что каждый ij-квадрат всегда пересекается со всеми полигонами топологического слоя, хотя является очевидным, что ни один квадрат из левого нижнего угла не может пересечься с полигонами верхнего правого угла (рисунок 4). Из этого следует, что в результате выполнения большего числа операции пересечения квадрата расчета локальной плотности с полигонами топологического слоя будет получено пустое множество точек.
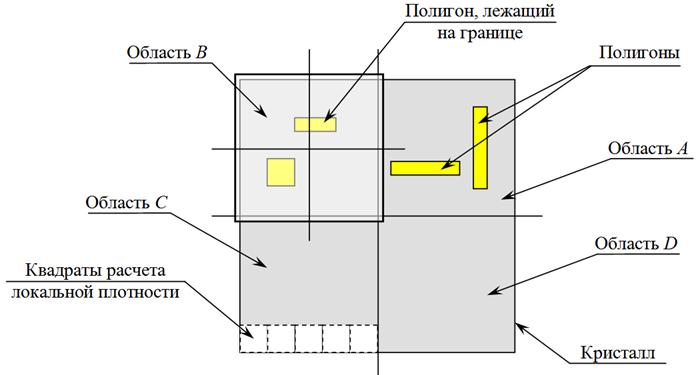
Рис. 4. Разбиение топологического слоя на области
Чтобы сократить вычислительные затраты необходимо провести, как бы «быстрое пересечение», которое позволит получить не окончательный результат, а только часть информации о взаимном расположении полигона и квадрата локальной плотности. Такой информацией может быть, например, определение того «лежит или нет полигон полностью внутри заданного квадрата».
В результате перед выполнением операций пересечения между квадратом расчета локальной плотности заполнения и полигонами топологического слоя всю область кристалла можно разбить на несколько областей, не прибегая при этом к использованию алгоритма, определяющего пересечение двух полигонов.
Для сортировки полигонов достаточно проверить, расположен ли он полностью в некоторой области, т.е. принадлежат ли все его вершины этой области. Тогда, например, полигоны, полностью лежащие в области A, не могут пересекаться с полигонами, полностью лежащими в области C. Такой подход снижает число вызовов алгоритма, определяющего пересечение полигонов, в результате чего затраты времени на вычисления сокращаются.
Дальнейшее разбиение топологического слоя также будет приводить к сокращению числа операций. Это вытекает из следующих соображений. Пусть после первого разделения в областях A, B, C, D (рисунок 4) число полигонов будет NA, NB, NC, ND, а число квадратов расчета локальной плотности заполнения в каждой из них равно: KI = K/4. Тогда число операций пересечения полигонов в каждой из областей составит RX = KI×NX, а суммарное число операций пересечения:

Из полученного выражения видно, что общее число операций R снизилось в четыре раза. Тогда, если каждую из полученных областей рекурсивно разбивать до тех пор, пока она не будет равна по размерам квадрату расчета локальной плотности, получим:

 , где r – глубина рекурсии.
, где r – глубина рекурсии.
Значит при глубине рекурсии равной 5, получим число операций пересечения двух полигонов равным R = K×N/1024. То есть число операций пересечения в этом случае сократится более чем в 1000 раз.
Еще одно преимущество описанного алгоритма разбиения топологического слоя на списки областей заключается в возможности его «распараллеливания», т.е. проведения одновременных вычислений на многоядерных или многопроцессорных системах. Причем число ядер (или процессоров) в данном случае ограничено только глубиной рекурсии. Так на каждую единицу увеличения глубины рекурсии, появляется возможность добавить шестнадцать новых вычислительных потоков (по четыре на каждую область).
При выполнении расчетов на основе рассмотренного далее алгоритма параллельность вычислений была обеспечена с использованием спецификации OpenMulti-Processing (далее OpenMP) из библиотеки программ на языке C++, поскольку ее применение обеспечивает наиболее простой интерфейс для возможности ведения параллельных вычислений, а также полностью поддерживается выбранным компилятором SunStudioC++.
В проведенном выше расчете было сделано допущение. Чтобы понять, в чем оно состояло, обратим внимание на полигон, лежащий на границе двух областей (рисунок 5), который относится сразу к нескольким областям. В этом случае выбор областей разбиения (см. рисунок 4) можно осуществить только путем пересечения сортируемого полигона с этой областью, что вытекает из того, что сами полигоны представляются набором точек – вершин полигона. Следовательно, нельзя утверждать, что если ни один из углов полигона не лежит в рассматриваемой области, то сам полигон не пересекается этой областью.
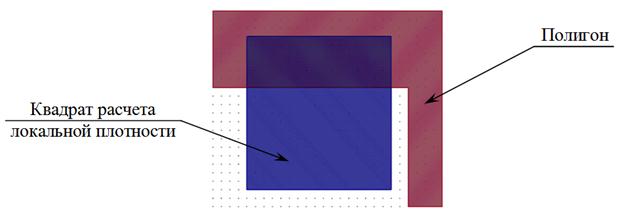
Рис. 5. Перекрытие полигона и квадрата расчета локальной плотности заполнения
Если же использовать алгоритм пересечения, с помощью которого вычисляется пересечение остальных полигонов, то фактического повышения быстродействия от их сортировки по областям получено не будет. Таким образом, при сортировке топологического слоя необходима дополнительная ускоренная обработка тех полигонов, которые целиком не были охвачены квадратом расчета плотности заполнения, что наиболее критично при очень маленькой сетке, используемой для ее расчета.
Прямоугольная оболочка полигона
Одна из возможностей, используя которую можно повысить скорость расчета локальной плотности заполнения, состоит в исключении полигонов, которые заведомо не пересекаются с рассматриваемым квадратом расчета плотности заполнения. Для ее реализации проведем проверку полигонов, основываясь на следующем их свойстве.
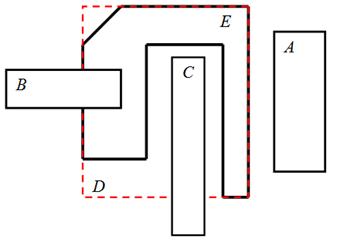
Рис. 6. Использование прямоугольной оболочки полигона для сокращения времени расчета
Пусть D – прямоугольная оболочка полигона E. Тогда некоторый полигон B пересекается с Е, только если B пересекается с D (рисунок 6). Так как по определению все точки полигона E лежат внутри оболочки D и, если ни одна точка полигона B не лежит в D, то полигоны B и Е не пересекаются.
Учет данного свойства дает следующие преимущества. Если обычно для определения области, к которой следует отнести полигон при сортировке, необходимо пересечь квадрат расчета локальной плотности с полигоном, то в случае учета описанного свойства достаточно вычислить только пересечение двух прямоугольников. Например, из рисунка 7 видно, что если прямоугольник D не пересекает квадрат расчета локальной плотности заполнения, то нет смысла проводить вычисления, применяя более сложный алгоритм определения пересечений двух полигонов.
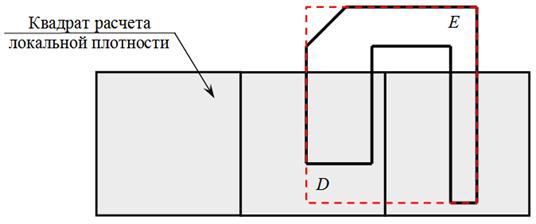
Рис. 7. Сортировка полигонов с использованием прямоугольной оболочки
В свою очередь два прямоугольника пересекаются только в том случае, когда выполняется следующее условие [5]:
 (1)
(1)
где ![]() – координаты вершин левого нижнего и правого верхнего углов рассматриваемых прямоугольников.
– координаты вершин левого нижнего и правого верхнего углов рассматриваемых прямоугольников.
Общий алгоритм расчета локальной плотности
Опишем общий алгоритм расчета локальной плотности заполнения топологического слоя с использованием всех ранее приведенных свойств полигонов.
С этой целью сначала представим весь топологический слой СБИС в виде связанного списка, включающего в себя множество полигонов принадлежащих этому слою. Затем разобьем топологический слой на четыре квадрата (рисунок 4), и на основе первоначального списка сформируем следующие три типа списков: F, R и P.
Списки типа F хранят информацию о полигонах, которые полностью лежат в одном из четырех квадратов.
Список типа R хранит информацию о полигонах, представляющих собой прямоугольники, не лежащие полностью ни в одном из квадратов.
Списки типа P хранят информацию о полигонах, которые пересекаются с соответствующим квадратом расчета локальной плотности заполнения.
Общее число списков равно девяти (по четыре списка F- и P-типов и один список R-типа).
Предположим, что изначально информация о топологическом слое хранится только в одном F-cписке и проведем ее сортировку с учетом вышеизложенных свойств полигонов. В результате получим списки F1-F4, R и P1-P4 (рисунок 8).Затем повторим указанную сортировку для каждого из полученных квадратов, используя, например, для первого квадрата списки F1, R, P1.Сортировку будем проводить до тех пор, пока размер области не станет меньшим, чем размер квадрата расчета локальной плотности заполнения. Затемдля полигонов F-списка вычислим их площадь, а для прямоугольников списка R пересечение с квадратом расчета локальной плотности заполнения проведем на основе неравенств (1), после чего вычисли площадь полученного прямоугольника.

Рис. 8. Сортировка полигонов по спискам при разбиении топологии
Далее для полигонов из P-списков с использованием алгоритма Сазерлэнда-Ходжмана [4] вычислим пересечения. Выбор указанного алгоритма правомочен, поскольку отсекающий полигон имеет форму квадрата (квадрата расчета локальной плотности заполнения), т.е. является выпуклым. Наконец, после выполнения операции пересечения вычислим площадь оставшегося в результате отсечения полигона.
Методы модификации топологии СБИС структурами заполнения
Процесс добавления dummy-структур в топологический слой обычно называют «заполнением топологии», так как топология заполняется относительно небольшими элементами одинаковой формы. Обычно dummy-структуры представляют собой одинаковых размеров прямоугольники или квадраты. Однако это могут быть и полигоны более сложной формы.
Методы заполнения могут быть разделены на две категории: с использованием описанных на специальном языке правил заполнения (далее RBDF, Rule-basedDummyFill) и с использованием моделирования (далее MBDF, Model-basedDummy Fill). При использовании RBDF-метода делается допущение, что толщина межслойного диэлектрика имеет прямо пропорциональную зависимость от локальной плотности заполнения для области кристалла размером порядка 500×500 мкм2. После чего в каждую область добавляется некоторое число dummy-структур так, чтобы проверка правил проектирования дала положительный результат.
При заполнении с помощью RBDF-метода возникает основная проблема, заключающаяся в том, что равномерное распределение локальной плотности заполнения не гарантирует минимального разброса толщины межслойного диэлектрика после операции ХМП. Однако при этом введение структур заполнения в топологию без оптимизации их расположения все же позволяет снизить разброс толщины межслойного диэлектрика после операции ХМП по сравнению с топологией без структур заполнения.
Далее будет рассмотрен алгоритм заполнения топологии слоя СБИС на основе модели, предложенной в работе [6], а также проведено его сравнение с методом заполнения топологии с помощью набора правил.
Алгоритм заполнения топологии СБИС
По сути, задача размещения структур заполнения на основе метода моделирования является оптимизационной задачей. Ее можно сформулировать следующим образом. Пусть допустимым множеством является разрешенные расположения структур заполнения, полученные в результате предыдущих шагов, а целевой функций – разброс толщины межслойного диэлектрика (max(Z(x,y))–min(Z(x,y)) или std(Z(x,y)), где Z(x,y) – распределение толщины межслойного диэлектрика).
Входной информацией для алгоритма является: топология рабочей области кристалла СБИС, ограничения на критерии остановки алгоритма (максимальное число итераций и минимальное изменение целевой функции std(Z(x,y))k+1–std(Z(x,y))k, где k – текущая итерация алгоритма), форма структуры заполнения и ограничения по локальной плотности заполнения для технологической операции плазмохимического травления (ПХТ). Результатом работы алгоритма заполнения является топология слоя СБИС с размещенными структурами заполнения согласно заданным ограничениям.
Алгоритм добавления структур заполнения на основе метода моделирования ХМП показан на рисунке 9. Заполнение топологического слоя СБИС dummy-структурами начинается с выделения областей доступных для заполнения. Для этого первоначально в топологическом слое определяются области с некоторым отступом от рисунка межсоединений. Отступ задается правилами проектирования для dummy-структур.
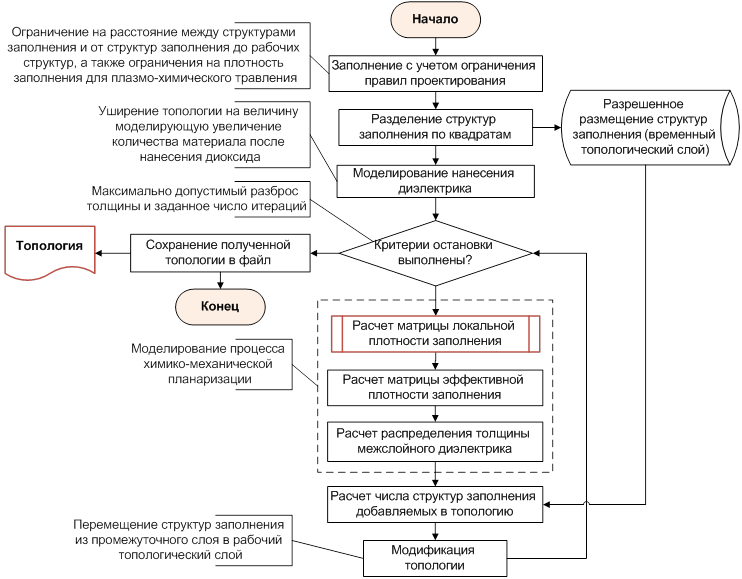
Рис. 9. Алгоритм MBDF-метода для заполнения топологического слоя СБИС
Второй шаг алгоритма состоит в предварительном заполнении топологического слоя СБИС с целью, чтобы были выполнены требования для операции ПХТ по минимальной и максимальной плотности заполнения. В результате выполнения двух шагов остается некоторое число dummy-структур, которые либо могут быть добавлены в топологический слой, либо нет, в зависимости от результата моделирования операции ХМП. Заключительный этап представляет собой цикл, задача которого состоит в выборке требуемого числа dummy-структур из слоя заполнения для каждого из квадратов, в котором проводится моделирования операции ХМП. Во время выполнения цикла расчет числа добавляемых структур заполнения для каждого из квадратов моделирования осуществляется по следующим выражениям:
![]()
где G – коэффициент («скорость заполнения»), [◦] – оператор округления до ближайшего целого числа, zср – среднее значение толщины диоксида. Полученные значения Nijпреобразуются согласно следующему выражению:

где Nij max – максимальное число структур заполнения для ij-квадрата. Это преобразование необходимо, поскольку число добавляемых в квадрат структур заполнения не может быть большим максимально допустимого числа, заранее установленного ранее по результатам анализа входной топологической информации.
Из приведенных выражений видно, что во время своей работы алгоритм, основываясь на промоделированном распределении толщины, приводит значение толщины остаточного диоксида кремния к среднему значению. Выражения для расчета числа добавляемых структур заполнения ранее были предложены в работе [7].
Результаты применения различных алгоритмов заполнения
Рассмотрим пример модификации топологического слоя СБИС dummy-структурами при использовании методов RBDF и MBDFдля топологии первого уровня металлизации тестового кристалла, содержащего два блока статической памяти (СОЗУ) и набор тестовых структур. Общий вид модифицируемого топологического слоя и «характерные» для заполнения области тестового кристалла показаны на рисунке 10.

Рис. 10. Общий вид тестового кристалла до и после заполнения, Справа внизу – гистограмма распределения плотности заполнения для RBDF-метода
Заполнение по методу, основанному на наборе правил, осуществлялось с помощью системы автоматизированного проектирования «Calibre» компании «MentorGraphics». Данная САПР позволяет с помощью написанных на языке разработанного фирмой «MentorGraphics» сценариев SVRF (StandardVerificationRuleFormat) заполнять топологический слой dummy-структурами с учетом определенных ограничений, каковыми могут быть ограничения на диапазон локальных плотностей заполнения в каждом квадрате топологии кристалла СБИС и градиент их изменения между соседними квадратами.
Результат применения RBDF-метода показан на рисунке 11а, из которого видно, что вся площадь кристалла заполнена dummy-фигурами равномерно в квадратах размером 500×500 мкм2. С целью оценки качества заполнения с использованием данного метода использовалась гистограмма распределения локальной плотности заполнения, которая приведена на рисунке 10. Из нее видно, что примерно 80% квадратов имеют локальную плотность заполнения 30-40%, а ее разброс не превышает 10%.
Заполнение MBDF, согласно алгоритму, приведенному на блок-схеме (рисунок 9), проводится в несколько шагов. На первом шаге для обеспечения необходимых требований по выполнению операции ПХТ слоя металлизации с помощью САПР «Calibre» весь кристалл заполнялся dummy-структурами с ограничениями на локальную плотность заполнения от 30% до 70%. Результат заполнения в виде карты локальной плотности заполнения представлен на рисунке 11а для RBDF-метода и на рисунке 11б для MBDF-метода.

(а) (б)
Рис. 11. Локальная плотность заполнения по RBDF-методу (а) и MBDF-методу (б)
Рассмотрим распределение полученной локальной плотности заполнения после заполнения различными методами (рисунок 11). В данном случае расчет локальной плотности заполнения проводился по квадратам размером 20×20 мкм2. Из рисунков 11а и 11б видно, что при использовании метода MBDF плотность заполнения неравномерна, а при использовании метода RBDF плотность заполнения самих dummy-структур равномерна, в том числе в зонах расположения блоков памяти, имеющих высокую плотность рисунка топологического слоя, в то время как при использовании метода MBDF блоки памяти окружены редкими dummy-структурами.

(а) (б)
Рис. 12. Распределение толщины межслойного диэлектрика после моделирования операции ХМП по методу RBDF (а) и методу MBDF (б)
Полученные в результате моделирования распределения остаточной толщины межслойного диэлектрика показаны на рисунке 12, из которого видно, что разброс толщины при заполнении на основе моделирования операции ХМП значительно меньше, нежели при заполнении по RBDF-методу.

(а) (б)
Рис. 13. Гистограмма распределения толщины диоксида кремния после моделирования операции ХМП для RBDF (а) и MBDF (б)
Количественное описание полученных результатов более наглядно представлено в виде гистограмм, приведенных на рисунке 13. На рисунке видно, что при заполнении топологического слоя dummy-структурами на основе метода моделирования дисперсия разброса толщины межслойного диэлектрика существенно меньше, что позволяет радикально уменьшить остаточный рельеф поверхности кристалла СБИС после выполнения операции ХМП.
Выводы
Предложенный алгоритм расчета локальной плотности заполнения топологического слоя субмикронных СБИС позволяет проводить моделирование операции ХМП без использования других САПР, что дает возможность адекватно оценивать форму рельефа поверхности межслойной изоляции в процессе производства СБИС. В свою очередь завершенный цикл моделирования операции ХМП позволит разработать более совершенные алгоритмы оптимального заполнения топологического слоя dummy-структурами,
На примере тестового кристалла с помощью модельных исследований показаны преимущества предлагаемого метода заполнения топологии СБИС dummy-структурами перед стандартным способом, основанном на контроле правил проектирования. Представлен результат заполнения топологического слоя тестового кристалла dummy-структурами, из которого видно существенное снижение разброса толщины диоксида кремния.
Литература
1. Y. Li, Microelectronic Applications Of Chemical-Mechanical Planarization [Text] : Wiley Interscience, 2008. – 734p. – ISBN 978-0-471-71919-9.
2. C. C. Chiang, J. Kawa, Design For Manufacturability And Yield For Nano-Scale CMOS [Text] : Springer, 2007. – 251 стр.
3. R. DeJule. Dual-Damascene: Overcoming Process Issues / Ruth DeJule: [Электронный ресурс].(http://www.semiconductor.net/article/204962-Dual_Damascene_Overcoming_Process_Issues.php). Проверено 09.04.2010.
4. Вычислительная геометрия и компьютерная графика на C++ [Текст] : монография / М.Ласло; Пер. с англ. В. Львова. - М. : Бином, 1977. – 301 с. : ил. - Пер. изд. : Computation algeometry and computer graphics in C++ / M. J. Laszlo. - S.l., 1996. - 5000 экз.
5. Препарата Ф. Вычислительная геометрия: введение [Текст] / Ф. Препарата, М. Шеймос ; Пер. с англ. - М. : Мир, 1989. - 478 с. - ISBN 5-03-001041-6.
6. Гладких А.А. Анализ повторяемости и точности моделирования операции химико-механической планаризации слоя двуокиси кремния. – М.: Издательство МГТУ им. Баумана, 13-я Молодежная международная научно-техническая конференция «Наукоемкие технологии и интеллектуальные системы 2011», 2011. – стр. 324-338
7. A. Kahng, G. Robins, A. Singh, and A. Zelikovsky. Filling Algorithms and Analyses for Layout Density Control. IEEE Trans. CAD, 18(4):445-462, April 1999.
Публикации с ключевыми словами: моделирование, dummy-структуры, кристаллы, полигоны, химико-механическая планаризация, СБИС
Публикации со словами: моделирование, dummy-структуры, кристаллы, полигоны, химико-механическая планаризация, СБИС
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||




