научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 02, февраль 2013
DOI: 10.7463/0213.0539000
УДК 519.6
Россия, МГТУ им. Н.Э. Баумана
Введение
Параллельные манипуляторы, основанные на платформе Стюарта, в настоящее время широко применяются для многих механизмов. По сравнению с последовательными манипуляторами, они обладают некоторыми преимуществами: высокая жесткость и точность позиционирования, хорошие динамические характеристики. В практике обычно используют параллельные манипуляторы с тремя или шестью степенями свободы, например робот «Дельта» имеет три степени свободы, гексапод ‑ шесть степеней свободы [1]. Чтобы повысить рабочие характеристики робота, параллельные манипуляторы могут соединяться между собой, образуя многосекционные параллельные роботы-манипуляторы.
Додекапод представляет собой развитие гексапода и имеет 12 степеней свободы. Додекапод по сравнению с гексаподом имеет большее рабочее пространство и используется для многих целей, например, на его основе может быть построен робот, перемещающийся по сложной поверхности или в трубе переменного профиля [2, 3].
В работе с помощью метода Денавита-Хартенберга [4] выполнено исследование кинематики односекционного параллельного манипулятора типа додекапод.
1. Постановка задачи
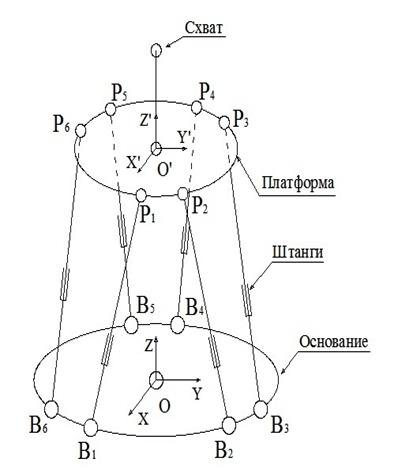
Приведем прежде схему гексапода (рисунок 1а). Гексапод состоит из неподвижного основания и подвижной платформы, соединенных между собой шестью штангами типа шарнир-призма-шарнир (ШПШ). Схват манипулятора крепится к платформе. Штанги связаны с основанием сферическими шарнирами ![]() , а с платформой – шарнирами Гука.
, а с платформой – шарнирами Гука.
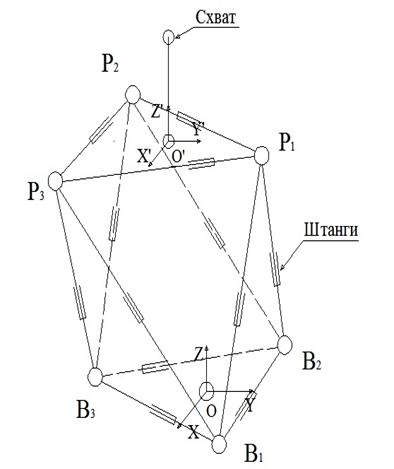
Додекапод состоит из 12 штанг и шести шарнирных узлов (рисунок 1б). В отличия от гексапода, додекапод не имеет основания и платформы. Можно сказать, что додекапод является развитием гексапод, в том смысле, что все шарниры могут в нем перемещаться относительно друг друга. Благодаря этому додекапод может быть использован для построения мобильных роботов, перемещающихся в сложной среде. Штанги додекапода также, как штанги гексапода, имеют тип ШПШ.
а) б)
Рисунок 1- Структура гексапода (а) и додекапода (б)
Задача анализа кинематики додекапода заключается в установлении отношений между длинами штанг ![]() и положениями узлов
и положениями узлов ![]() ,
, ![]() . Задача разделяется на две подзадачи ‑ прямая позиционная задача и обратная позиционная задача. Прямую позиционную задачу формулируют следующим образом: известны длины штанг манипулятора
. Задача разделяется на две подзадачи ‑ прямая позиционная задача и обратная позиционная задача. Прямую позиционную задачу формулируют следующим образом: известны длины штанг манипулятора ![]() . Требуется найти координаты всех узлов
. Требуется найти координаты всех узлов ![]() ,
, ![]() . Обратная позиционная задача формулируется как задача отыскания длин штанг
. Обратная позиционная задача формулируется как задача отыскания длин штанг ![]() по известным положениям узлов манипулятора
по известным положениям узлов манипулятора ![]() ,
, ![]() .
.
Рассматриваем частный случай, когда узлы ![]() ,
, ![]() образуют равносторонние треугольники. Задача такого сорта возникает при изучении движения додекапода в прямолинейной трубе постоянного или переменного сечения. Додекапод при этом можно рассматривать как гексапод, в котором совпадают пары шарниров (
образуют равносторонние треугольники. Задача такого сорта возникает при изучении движения додекапода в прямолинейной трубе постоянного или переменного сечения. Додекапод при этом можно рассматривать как гексапод, в котором совпадают пары шарниров (![]() ), (
), (![]() ), (
), (![]() ), а также пары шарниров (
), а также пары шарниров (![]() ), (
), (![]() ), (
), (![]() ). Подобно гексаподу назовем треугольник
). Подобно гексаподу назовем треугольник ![]() основанием додекапода, а треугольник
основанием додекапода, а треугольник ![]() – платформой.
– платформой.
2. Обратная позиционная задача
Положим, что начала координаты ![]() основания и платформы находятся в центрах треугольников
основания и платформы находятся в центрах треугольников ![]() и
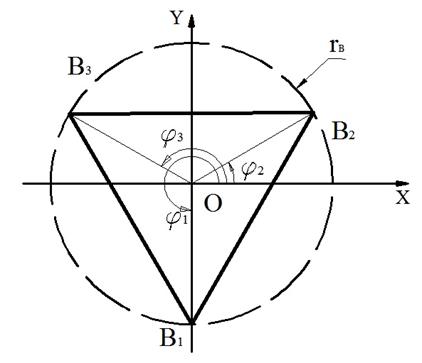
и ![]() соответственно (рисунок 2).
соответственно (рисунок 2).

а) б)
Рисунок 2 - Координаты шарниров на основание (а) и платформе (б)
Координаты шарниров ![]() на платформе и
на платформе и ![]() на основании определяются формулами
на основании определяются формулами
![]() , (1)
, (1)
![]() , (2)
, (2)
где ![]() – радиусы платформы и основания;
– радиусы платформы и основания; ![]() - полярные углы шарниров
- полярные углы шарниров ![]() и
и ![]() соответственно;
соответственно; ![]() - координаты шарнира
- координаты шарнира ![]() на платформе и шарнира
на платформе и шарнира ![]() на основании,
на основании, ![]() .
.
Для того чтобы определить длины штанг, нужно преобразовать координаты шарниров на платформе в систему координат ![]() на основание (рисунок 3).
на основание (рисунок 3).
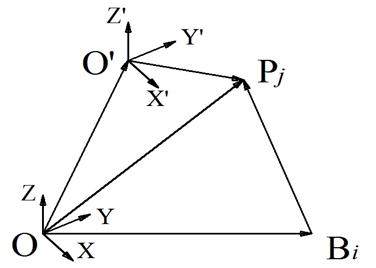
Рисунок 3 -Схема векторов для штанги ![]()
Из схемы, представленной на рисунке 3, следует справедливость формулы
![]() ,
, ![]() , (3)
, (3)
где компоненты векторов ![]() вычисляются по формулам вида (1), (2);
вычисляются по формулам вида (1), (2); ![]() – матрица перехода от системы координат
– матрица перехода от системы координат ![]() к системе координат
к системе координат ![]() ;
; ![]() - оператор скалярного произведения.
- оператор скалярного произведения.
Существуют различные методы перехода от системы координат ![]() к системе координат
к системе координат ![]() . Мы используем метод Ролла-Пича-Йора [2], который заключается в следующем: сначала начало системы координат
. Мы используем метод Ролла-Пича-Йора [2], который заключается в следующем: сначала начало системы координат ![]() по вектору переноса
по вектору переноса ![]() переносим в точку
переносим в точку ![]() . Затем последовательно поворачивать систему координат
. Затем последовательно поворачивать систему координат ![]() вокруг осей
вокруг осей ![]() на углы
на углы ![]() (рисунок 4).
(рисунок 4).

Рисунок 4. Трансформирование системы координат метода Ролла-Пича-Йора
Обобщенная матрица преобразования имеет в этом случае вид
 ,
,
где ![]() – матрица вращения, определяемая выражением
– матрица вращения, определяемая выражением

 ; (4)
; (4)
![]() – матрица переноса;
– матрица переноса; ![]() - матрица центрального проектирования;
- матрица центрального проектирования; ![]() – коэффициент масштабирования.
– коэффициент масштабирования.
Таким образом, используем обобщенную матрицу преобразования вида
 . (5)
. (5)
Алгоритм решения обратной задачи:
1) вычислить позиции всех точек ![]() по формулам (1), (2),
по формулам (1), (2),
2) определить матрицу преобразования ![]() по (4),(5),
по (4),(5),
3) вычислить длины всех штанг по формуле (3).
3. Прямая позиционная задача
При неизвестных параметрах ![]() , определяющих положение и ориентацию платформы, длины штанг платформы, полученные из формулы (3), являются корнями системы шести уравнений второго порядка
, определяющих положение и ориентацию платформы, длины штанг платформы, полученные из формулы (3), являются корнями системы шести уравнений второго порядка
 , (6)
, (6)
где ![]() – координаты шарнира
– координаты шарнира ![]() на основании;
на основании; ![]() - координаты шарнира
- координаты шарнира ![]() на платформе;
на платформе; ![]() - матрицавращения (4);
- матрицавращения (4); ![]() .
.
Систему (6) решаем методом сведения к задаче нелинейного программирования
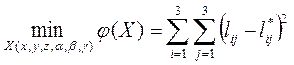 , (7)
, (7)
где
 .
.
Для решения задачи (7) используем метод роя частицами [5]. Полагаем, что положение частицы в пространстве поиска определяет вектор ![]() , а функция приспособленности частицы равна
, а функция приспособленности частицы равна
 . (8)
. (8)
Алгоритм метода роя частиц.
1) Инициализируем популяцию из ![]() частиц, положение каждой из которых определяет вектор X.
частиц, положение каждой из которых определяет вектор X.
2) Для каждой из частиц ![]() по формуле (7) вычисляем значение функции (8).
по формуле (7) вычисляем значение функции (8).
3) Вычисляем текущие приращения положения частиц
![]() , (9)
, (9)
где ![]() ;
;![]() ;
; ![]() - (6х1) - вектор случайных чисел, равномерно распределенных в интервале
- (6х1) - вектор случайных чисел, равномерно распределенных в интервале ![]() ;
;![]() - символ прямого произведения векторов;
- символ прямого произведения векторов; ![]() - вектор координат частицы, соответствующий ее наилучшему значению функции приспособленности в течение всех предыдущих итераций, то есть
- вектор координат частицы, соответствующий ее наилучшему значению функции приспособленности в течение всех предыдущих итераций, то есть
![]() ;
;
![]() - вектор координат соседней с данной частицы (в смысле используемой топологии соседства) с наилучшим значением приспособленности, т.е.
- вектор координат соседней с данной частицы (в смысле используемой топологии соседства) с наилучшим значением приспособленности, т.е.
![]() ,
,
где ![]() - множество соседей частицы
- множество соседей частицы ![]() .
.
4)Находим новые позиции всех частиц популяции по формуле
![]() . (10)
. (10)
5) Повторяем шаги 2 – 4 до выполнения условия окончания итераций, например, до достижения заданного числа итераций.
Пример.
Пусть длины штанг манипулятора равны
![]() ;
;
радиусы основания и платформы ![]() . Положения шарниров на основании определяют углы
. Положения шарниров на основании определяют углы  , а на платформе
, а на платформе  .
.
Используем метод роя частиц с параметрами: число частиц ![]() , число итерации
, число итерации ![]() . Для повышения вероятности локализации глобального экстремума используем метод мультистарта с числом стартов K=30.
. Для повышения вероятности локализации глобального экстремума используем метод мультистарта с числом стартов K=30.
Результат решения задачи иллюстрирует рисунок 5.
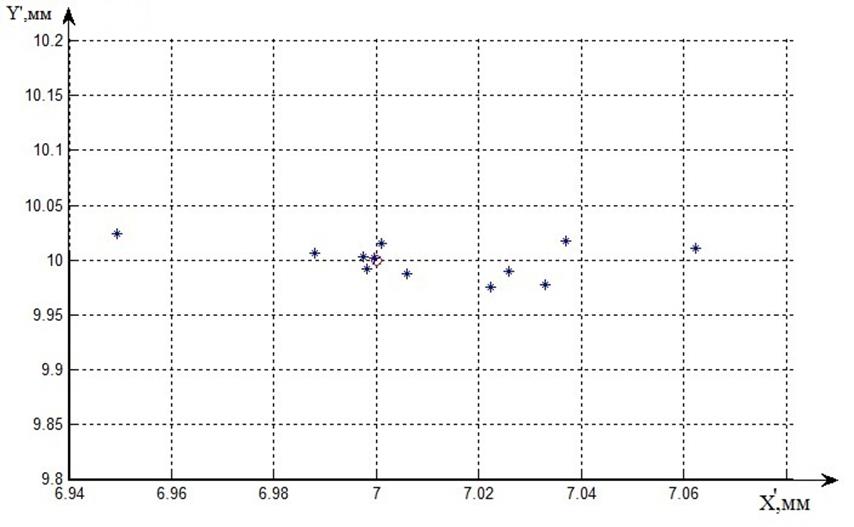
Рисунок 5 - Полученные наилучшие частицы на плоскость ![]()
На рисунке 5 красная точка – точное положение точки ![]() ; синие точки – 11 лучших решений по результатам 30 стартов.
; синие точки – 11 лучших решений по результатам 30 стартов.
Полученные результаты показывают высокую скорость сходимости алгоритма. Сходимость метода роя частиц иллюстрирует рисунок 6.
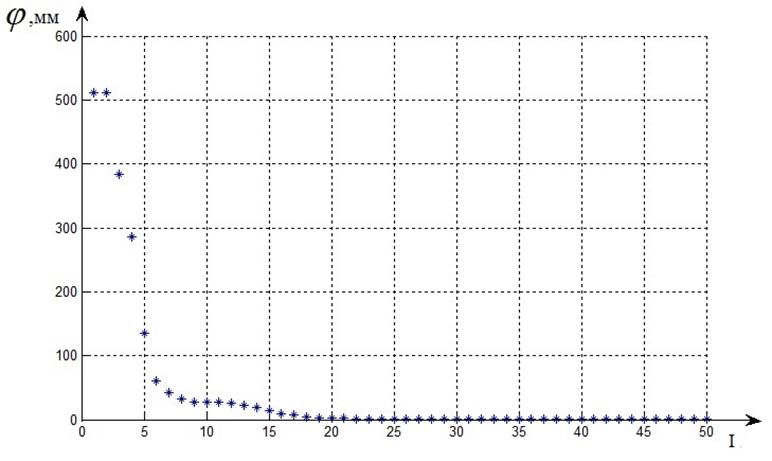
Рисунок 6 – Сходимость метода роя частиц
Представленные результаты получены с помощью программного обеспечения, разработанного в среде Matlab.
4. Ориентация платформы
Положение и ориентация платформы ![]() могут быть заданы двумя способами.
могут быть заданы двумя способами.
1) Задание положения начальной точки ![]() и переход от системы координат, связанной с основанием, к системе координат, связанной с платформой, методом Ролла-Пича-Йора с углами
и переход от системы координат, связанной с основанием, к системе координат, связанной с платформой, методом Ролла-Пича-Йора с углами ![]() .
.
2) Задание положения начальной точки ![]() и направленного вектора
и направленного вектора ![]() .
.
Рассматриваем задачу перехода от первого представления ко второму, т.е. задачу
![]() . (11)
. (11)
Направленный вектор ![]() в системе координат
в системе координат ![]() имеет координаты
имеет координаты ![]() в системе координат
в системе координат ![]() , то есть
, то есть  .(12)
.(12)
Из (12) следует, что
 (13)
(13)
Если платформа не вращается, то ![]() . Тогда
. Тогда
 (14)
(14)
Если платформа вращается на угол ![]() вокруг оси
вокруг оси ![]() , то
, то ![]() . Тогда имеем
. Тогда имеем
 (15)
(15)
Заключение
В работе решены прямая и обратная задача кинематики односекционного манипулятора параллельной структуры типа «додекапод». Прямая задача решена с использованием метода роя частиц, который дает быстрый поиск с минимумом меньше чем ![]() . Результаты работы предполагается в последующем использовать для отыскания рабочего пространства додекапода, а также для решения задачи его динамики. С помощью матрицы трансформирования положения и ориентация любой плоскости может выражаться двумя способами: по направленному вектору или по трансформированию.
. Результаты работы предполагается в последующем использовать для отыскания рабочего пространства додекапода, а также для решения задачи его динамики. С помощью матрицы трансформирования положения и ориентация любой плоскости может выражаться двумя способами: по направленному вектору или по трансформированию.
Список литературы
1. Merlet J.P. Parallel Robots. KluwerAcademicPublishers, 2000. 394 p.
2. Саяпин С.Н., Синев А.В. Адаптивный мобильный пространственный робот-манипулятор и способ организации движений и контроля физико-механических свойств и геометрической формы контактируемой поверхности и траектории перемещения с его помощью: пат. 2424893 РФ. 2011.
3. Зенкевич С.Л., Юшенко А.С. Основы управления манипуляционными роботами. М.: МГТУ им. Н.Э. Баумана, 2004. 114 с.
4. Bande P., Seibt M., Uhlmann E., Saha S.K., Rao P.V.M. Kinematics analyses of Dodekapod // Mechanism and Machine Theory. 2005. Vol. 40, no. 6. P. 740-756. DOI: 10.1016/j.mechmachtheory.2004.11.006
5. Карпенко А.П., Селиверстов Е.Ю. Обзор методов роя частиц (PSO) для задачи глобальной оптимизации // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2009. № 3. Режим доступа: http://technomag.edu.ru/doc/116072.html (дата обращения 21.12.2012).
Публикации с ключевыми словами: метод роя частиц, додекапод, параллельный манипулятор, кинематика додекапода, Ролл-Пич-Йор
Публикации со словами: метод роя частиц, додекапод, параллельный манипулятор, кинематика додекапода, Ролл-Пич-Йор
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



