научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 08, август 2013
DOI: 10.7463/0813.0587740
УДК 519.6
Россия, МГТУ им. Н.Э. Баумана
ФГБУН «Институт машиноведения им. А.А. Благонравова РАН (ИМАШ РАН)
Введение
Благодаря своей универсальности и функциональным возможностям додекапод может быть успешно применен в качестве базового модуля в робототехнических системах, предназначенных для решения широкого круга задач в интересах силовых структур, здравоохранения и экономики страны. При этом додекапод может эксплуатироваться, как индивидуально, так и коллективно, в составе роевых интеллектуальных робототехнических систем, способных самоорганизовываться и объединять додекаподы в пространственные линейные или поверхностные активные структуры для решения широкого круга более сложных задач, например, совместное преодоление препятствий и др. Поэтому исследование функциональных возможностей додекапода актуально.
Додекапод представляет собой односекционный параллельный манипулятор, который можно считать развитием широко известного гексапода или платформы Стюарта [1]. Идея додекапода представлена в работе [2]. В этой работе, а также в работах [3, 4] рассмотрены возможности использования додекапода как мобильного пространственного робота-манипулятора, перемещающегося по сложной поверхности или в трубе переменного профиля. В публикации [5] представлены результаты исследования кинематики додекапода.
В статье рассматривается одна из функциональных возможностей додекапода - движение в прямолинейной цилиндрической трубе постоянного и переменного сечений.
1. Схема додекапода и основные обозначения
Додекапод состоит из шести шарнирных узлов ![]() и двенадцати штанг переменной длины, соединяющих эти узлы (рисунок 1). Узлы
и двенадцати штанг переменной длины, соединяющих эти узлы (рисунок 1). Узлы ![]() и
и ![]() определяют две параллельные плоскости. При движении додекапода в цилиндрической трубе, как постоянного, так и переменного сечений, эти тройки узлов играют роль упоров. Когда, например, тройка узлов
определяют две параллельные плоскости. При движении додекапода в цилиндрической трубе, как постоянного, так и переменного сечений, эти тройки узлов играют роль упоров. Когда, например, тройка узлов ![]() фиксирована, узлы
фиксирована, узлы ![]() могут перемещаться вдоль трубы за счет одновременного изменения длин боковых штанг
могут перемещаться вдоль трубы за счет одновременного изменения длин боковых штанг ![]() (рисунок 2). Принимаем, что в процессе движения додекапода отсутствует проскальзывание шарниров.
(рисунок 2). Принимаем, что в процессе движения додекапода отсутствует проскальзывание шарниров.
Введем следующие основные обозначения:
![]() ‑ минимальная и максимальная длины штанг додекапода;
‑ минимальная и максимальная длины штанг додекапода;
![]() ‑ диаметр шарнира додекапода;
‑ диаметр шарнира додекапода;
![]() ‑ длины штанг на гранях
‑ длины штанг на гранях ![]() ,
, ![]() , когда соответствующие узлы соприкасаются с внутренней поверхностью трубы;
, когда соответствующие узлы соприкасаются с внутренней поверхностью трубы;
![]() ‑ минимальное расстояние между плоскостями
‑ минимальное расстояние между плоскостями ![]() ,
, ![]() (когда длины боковых штанг достигают минимальной длины);
(когда длины боковых штанг достигают минимальной длины);
![]() - максимальное расстояние между плоскостями
- максимальное расстояние между плоскостями ![]() ,
, ![]() (когда длины боковых штанг достигают максимальной длины);
(когда длины боковых штанг достигают максимальной длины);
![]() – шаг движения додекапода.
– шаг движения додекапода.
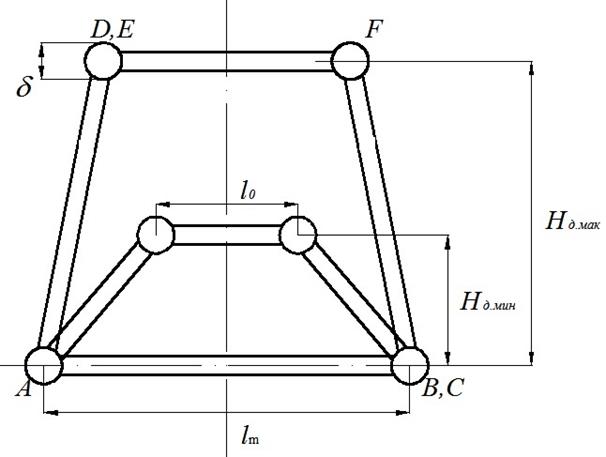
Рисунок 1 – Схема додекапода

а) б)
Рисунок 2 - Додекапод в цилиндрической трубе постоянного сечения: а) передний вид; б) боковой вид
2. Алгоритм движения додекапода в прямолинейной трубе постоянного сечения
Пусть труба имеет внутренний диаметр ![]() . Для того, чтобы в процессе движения додекапод прочно фиксировался в трубе, треугольники
. Для того, чтобы в процессе движения додекапод прочно фиксировался в трубе, треугольники ![]() ,
, ![]() должны быть равносторонними и их плоскости должны быть перпендикулярны оси симметрии трубы (рисунок 3).
должны быть равносторонними и их плоскости должны быть перпендикулярны оси симметрии трубы (рисунок 3).
Из рисунка 3 имеем равенство
 .
.
С учетом очевидного ограничения ![]() , из этого равенства получаем условие
, из этого равенства получаем условие
 . (1)
. (1)
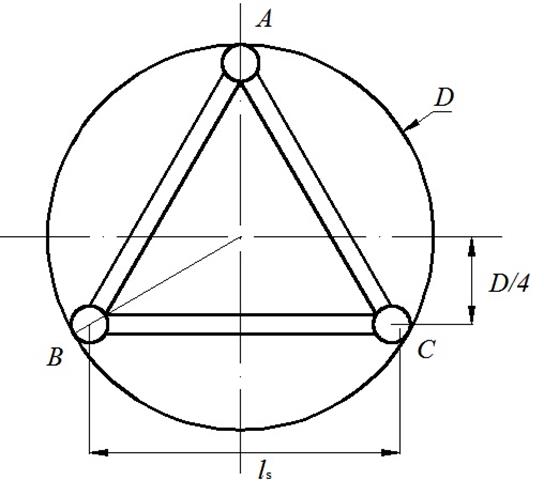
Рисунок 3 – К определению длин штанг додекапода
Алгоритм движения додекапода имеет следующий вид (рисунок 4).
1) Задаем начальные положения длин штанг и начальные положения шарниров:
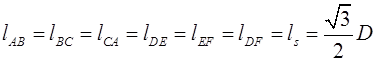 ;
; ![]() .
.
2) Уменьшаем длины штанг ![]() со значения
со значения ![]() до величины
до величины ![]() .
.
3) Аналогично уменьшаем длины штанг ![]() с
с ![]() до
до ![]() .
.
4) Увеличиваем длины штанг ![]() с
с ![]() до
до ![]() .
.
5) Уменьшаем длины штанг ![]() с
с ![]() до
до ![]() .
.
6) Увеличиваем длины штанг![]() с
с ![]() до
до ![]() .
.
7) Увеличиваем длины штанг ![]() с
с ![]() до
до ![]() . В результате додекапод перемещается вправо на шаг
. В результате додекапод перемещается вправо на шаг ![]() .
.
8) Повторяем шаги 2-7 требуемое число раз.
Движение додекапода в прямолинейной трубе постоянного сечения иллюстрирует рисунок 4.

а) б) в) г)

д) з) ж)
Рисунок 4 – Эатпы движения додекапода в трубе постоянного сечения а) начальное состояние; б) – г) левая грань движется вперёд; д) –ж) правая грань движется вперёд
3. Алгоритм движения додекапода в прямолинейной трубе переменного сечения
Пусть цилиндрическая труба имеет две части постоянного сечения с диаметрами соответственно ![]() (длина
(длина ![]() ) и
) и ![]() (длина
(длина ![]() ) и переход от первой части ко второй длиной
) и переход от первой части ко второй длиной ![]() (рисунок 5).
(рисунок 5).

Рисунок 5 – Схема преодоления додекаподом перехода от трубы большего диаметра к трубе меньшего диаметра
В данной ситуации существует опасность столкновения боковых штанг додекапода с поверхностью трубы в переходе. Легко видеть, что для того, чтобы избежать столкновения, необходимо, во-первых, выполнение следующих очевидных неравенств:
 ;
;  . (2)
. (2)
Во-вторых, для корректного преодоления додекаподом перехода имеют место ограничения на максимально допустимую длину шага додекапода ![]() . Для определения этих ограничений рассмотрим два возможных положения додекапода на переходе (рисунок 6).
. Для определения этих ограничений рассмотрим два возможных положения додекапода на переходе (рисунок 6).

а) б)

в) г)
Рисунок 6 – Возможные положения додекапода на переходе трубы а) ‑ б) ‑ грань ABC находится в трубе большего диаметра; в) ‑ г) – грань ABC находится внутри перехода
3.1. Случай 1. Грань ![]() находится в первой части трубы (которая имеет диаметр
находится в первой части трубы (которая имеет диаметр ![]() ) – рисунок 7.
) – рисунок 7.

Рисунок 7 – К определению величины максимального шага додекапода: случай 1
Пусть начало ![]() системы координат
системы координат ![]() находится в центре трубы перед переходом. Легко видеть, что координаты шарнира
находится в центре трубы перед переходом. Легко видеть, что координаты шарнира ![]() в этой системе координат равны
в этой системе координат равны  , а шарнира
, а шарнира ![]() ‑
‑ 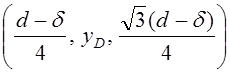 . Величина
. Величина ![]() принимает свое минимальное значение в ситуации, когда шарнир А находится в начале перехода, то есть имеет место неравенство
принимает свое минимальное значение в ситуации, когда шарнир А находится в начале перехода, то есть имеет место неравенство ![]() . Кроме того, из рисунка 7 имеем очевидное равенство
. Кроме того, из рисунка 7 имеем очевидное равенство ![]() .
.
Максимальное допустимое значение ![]() шаг додекапода принимает, если боковая штанга
шаг додекапода принимает, если боковая штанга ![]() касается правой границы перехода (когда диаметр перехода уже равен
касается правой границы перехода (когда диаметр перехода уже равен ![]() ). Эта точка касания на рисунке 7 обозначена
). Эта точка касания на рисунке 7 обозначена ![]() . Точка
. Точка ![]() находится на линии
находится на линии ![]() и расстояние ее до оси симметрии трубы равно
и расстояние ее до оси симметрии трубы равно  . Таким образом, имеет место система уравнений
. Таким образом, имеет место система уравнений
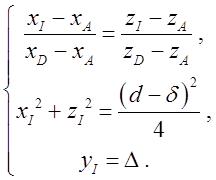 (3)
(3)
Решение системы уравнений (3) имеет вид

где
 .
.
Из рисунка 7 следует справедливость отношения
 ,
,
где
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Отсюда следует выражение
 . (4)
. (4)
Как вытекает из формулы (4), свое максимальное значение величина ![]() принимает при
принимает при ![]() .
.
Таким образом, имеем следующий алгоритм преодоления додекаподом перехода.
1) Если выполняется неравенство
![]() , (5)
, (5)
то грань ![]() сразу переходит в правую часть трубы с шагом
сразу переходит в правую часть трубы с шагом ![]() . Далее додекапод движется с постоянным шагом, равным
. Далее додекапод движется с постоянным шагом, равным ![]() .
.
2) В случае не выполнения неравенства (5), грань ![]() перемещается вперед с шагом
перемещается вперед с шагом ![]() .
.
3.2. Случай 2. Грань ![]() находится внутри перехода (рисунок 8).
находится внутри перехода (рисунок 8).

Рисунок 8 – К определению величины максимального шага додекапода: случай 2
В этом случае аналогично первому случаю координаты точек ![]() равны соответственно
равны соответственно
 ,
,  ,
,
где
 ,
,  .
.
Как и в случае 1, координаты ![]() точки
точки ![]() получаем путем решения систему уравнения (3). Из рисунка 8 следует справедливость отношения
получаем путем решения систему уравнения (3). Из рисунка 8 следует справедливость отношения  , где
, где ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Таким образом, в данном случае имеем следующее выражение для величины максимального шага додекапода:
 . (6)
. (6)
Вид функции ![]() иллюстрирует рисунок 9, из которого следует, что максимальное значение величина
иллюстрирует рисунок 9, из которого следует, что максимальное значение величина ![]() принимает при
принимает при  . Рисунок соответствует случаю
. Рисунок соответствует случаю ![]() .
.

Рисунок 9 – Значения максимального шага додекапода ![]() в функции величины
в функции величины ![]() : синяя линия -
: синяя линия - ![]() ; красная -
; красная - ![]() ; черная –
; черная – ![]()
Алгоритм движения додекапода по переходу имеет в случае 2 следующий вид.
1) Додекапод движется вперед с шагом ![]() до выполнения неравенства
до выполнения неравенства
![]() , (7)
, (7)
после чего грань ![]() перемещается сразу в правую часть труба с шагом
перемещается сразу в правую часть труба с шагом ![]() . Далее додекапод движется с постоянным шагом, равным
. Далее додекапод движется с постоянным шагом, равным ![]() .
.
2) Если неравенство (7) не выполнено, то преодоление додекаподом перехода невозможно.
В качестве простого приближенного условия возможности преодоления додекаподом перехода может быть использовано условие
 . (8)
. (8)
3.3. Алгоритм преодоления додекаподом сужения трубы имеет следующий вид.
1) Додекапод перемещается по левой части трубы (имеющей диаметр ![]() ) с шагом
) с шагом ![]() , который обеспечивает изменение длин боковых штанг в диапазоне
, который обеспечивает изменение длин боковых штанг в диапазоне 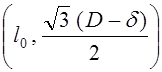 .
.
2) Если условие (8) выполняется, то додекапод останавливается – преодоление перехода невозможно. В противном случае додекапод преодолевает переход, выбирая шаг своего перемещения по формуле (4) или формуле (6).
3) Додекапод продолжает двигаться по правой части трубы (имеющей диаметр ![]() ) с шагом
) с шагом ![]() , который обеспечивает изменение длин боковых штанг в диапазоне
, который обеспечивает изменение длин боковых штанг в диапазоне  .
.
Данный алгоритм иллюстрирует рисунок 10.


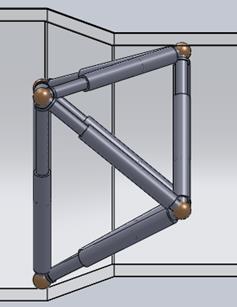
а) б) в)

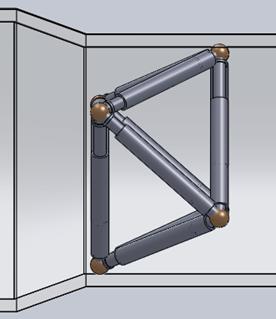
д) е)
Рисунок 10 – Этапы преодоления додекаподов сужения цилиндрической трубы
Из характера зависимости ![]() следует, что
следует, что
1) если ![]() (переход узкий), то додекапод может преодолеть переход, не меняя шага движения,
(переход узкий), то додекапод может преодолеть переход, не меняя шага движения,
2) если  , то
, то ![]() имеет малое значение, то есть додекапод преодолевает переход с малым шагом.
имеет малое значение, то есть додекапод преодолевает переход с малым шагом.
Заключение
В работе получены условия преодоления додекаподом сужения цилиндрической трубы, а также алгоритмы движения додекапода в прямолинейной цилиндрической трубе переменного сечения. Полученные результаты относятся к ситуации, когда додекапод переходит из трубы большего диаметра в трубу меньшего диаметра. Эти результаты легко переносятся на случай, когда додекапод преодолевает расширение трубы.
В развитие работы планируется разработка алгоритмов движения додекапода в непрямолинейных цилиндрических трубах, в таких же перекрещивающихся трубах, а также в не цилиндрических трубах (например, имеющих квадратное или эллиптическое сечение).
Список литературы
1. Merlet J.P. Parallel Robots. KluwerAcademicPublishers, 2000. P. 31-65.
2. Саяпин С.Н., Синев А.В. Адаптивный мобильный пространственный робот-манипулятор и способ организации движений и контроля физико-механических свойств и геометрической формы контактируемой поверхности и траектории перемещения с его помощью : пат. 2424893 РФ. 2011.
3. Саяпин С.Н. Додекапод как современный этап развития пространственных параллельных роботов // Проблемы машиностроения и надежности машин. 2012. № 6. С. 31-45.
4. Sayapin S.N. Parallel spatial robots of dodecapod type // Journal of Machinery Manufacture and Reliability. November 2012. Vol. 41, iss. 6. P. 457-466. DOI: 10.3103/S1052618812060143
5. Данг С.Х. Кинематика односекционного параллельного манипулятора типа «додекапод» // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2013. № 2. DOI: 10.7463/0213.0539000
Публикации с ключевыми словами: додекапод, параллельный манипулятор, цилиндрическая труба
Публикации со словами: додекапод, параллельный манипулятор, цилиндрическая труба
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



