научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2013
УДК 51-77:330.4:519.21
Тульский филиал Российского государственного торгово-экономического университета
Введение
На протяжении нескольких десятилетий в экономическую науку, в целом, и в эконометрику, в частности, широко внедряются методы исследований и математический аппарат, применяемые в физике. В частности, используется такое понятие как «энтропия».
Этому подходу посвящено много публикаций, среди которых следует отметить работы таких ученых, как В. Бурлачков [2], E.T. Jaynes [14], R. Kümmel [15], В.В. Глущенко [4], С.Д. Хайтун [9] и другие. Автор также применял подобный подход в исследованиях процессов контроля и управления в машиностроении [11].
Предложенный метод проводит аналогию между экономическими и термодинамическими процессами, что, с одной стороны, позволяет добиться новых интересных результатов, имеющих практическое значение, но, с другой стороны, не всегда позволяет получить интересующие практиков зависимости и оценить значимость моделей. Автор предлагает новый подход, базирующийся на методах теории информации, основанной К. Шенноном [10] и Н. Винером [3].
Постановка задачи
Как известно, практически все статистические методы исследования взаимосвязей предполагают, что модель является линейной либо может быть сведена к ней и все переменные, входящие в нее, имеют нормальное распределение. Если же эти допущения отсутствуют, то практически невозможно оценить значимость коэффициентов модели и получить надежные доверительные интервалы.
Еще в 1975 году Н.С. Райбман и В.М. Чадеев [8] показали, что корреляционные модели не дают надежных результатов. Более того, остаточная дисперсия, являющейся основой для оценки значимости параметров влияния факторов на признак, никоим образом не может служить мерой взаимодействия. Также возникают проблемы с определением законов распределения случайных величин. Как правило, в этих задачах используют критерий Пирсона, хотя структура его такова, что он дает достоверные результаты только при решении вопроса о нормальности распределения.
Толчок к широкому применению методов теории информации автор получил при изучении работ Г.П. Башарина [1] и С. Кульбака [5].
В предисловии к книге Кульбака [5] академик А.Н.Колмогоров писал: «... аналитический аппарат теории информации был создан тогда, когда здание математической статистики было в своих основных, находящих наиболее широкое применение, частях уже построено и кодифицировано. Но новые мысли и аналитический аппарат теории информации должны, по-видимому, привести к заметной перестройке этого здания».
Можно отметить, что 90-м годам XX века сформировался новый подход в разных областях науки и техники, который можно назвать «энтропийным подходом». Теория информации позволяет унифицировать известные результаты теории статистических выводов, что наглядно показано в работе С. Кульбака [5].
Анализ литературы, посвященной информационной теории управления, приводит к выводу, что «... информационный подход дает единую точку зрения на все виды управления, независимо от его цели и типа управления системы» [7]. Теория информации, как и статистическая физика, благодаря своим методам и обобщениям позволяет исследовать объекты сложной природы на относительно простых и наглядных математических моделях.
Изначально энтропия рассматривалась как мера величины, характеризующей процессы перехода тепловой энергии в механическую. Связь между энтропией как мерой неопределенности и термодинамической энтропией достаточно долго оставалась неясной, но в последней четверти ХХ века она была установлена [6].
Рассмотрим некоторые соотношения из теории информации, которые мы будем использовать в дальнейшем.
Энтропия, как мера связи
Пусть некоторая система имеет дискретный набор состояний х1, х2, …, хk, которые она может принимать с вероятностями p1, p2, …, pk. Тогда, согласно К. Шеннону [10], мера неопределенности или энтропия системы имеет следующее числовое значение
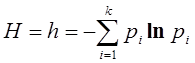 (1)
(1)
Вероятности, используемые в выражении (1), как правило, определяются опытным путем, следовательно, при расчетах, вместо точных значений приходится использовать эмпирические оценки, рассчитанные через частоты наблюдений соответствующих состояний, т.е. в качестве оценки энтропии будет использоваться величина
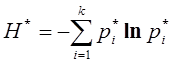 , (2)
, (2)
где 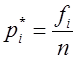 - частости; fi – частоты наблюдений соответствующих состояний; n – количество наблюдений (объем выборки).
- частости; fi – частоты наблюдений соответствующих состояний; n – количество наблюдений (объем выборки).
Как было показано Г.П. Башариным [1] при достаточно общих предположениях, в том числе и в предположении о стремлении количества состояний к бесконечности, статистическая оценка энтропии (2) имеет асимптотически нормальное распределение с параметрами
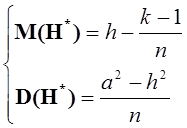 (3)
(3)
Здесь
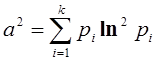 (4)
(4)
Параметры a2 и h в дальнейшем будем называть энтропийными параметрами распределения.
Приведенные выше соотношения справедливы для дискретных случайных величин, в то время как на практике мы имеем дело с непрерывными распределениями, в связи с чем приходится проводить процедуру дискретизации.
Пусть W(x) – функция плотности вероятности некоторой случайной величины Х с дисперсией σ2.
Нормируем случайную величину Х и введем новую случайную величину ![]() , имеющую функцию плотности w(x). Разобьем область изменения случайной величины на интервалы шириной ∆х. Пронумеруем эти интервалы от нижней до верхней границы числами натурального ряда от 1 до k. Пусть вероятности попадания в каждый интервал равны соответственно
, имеющую функцию плотности w(x). Разобьем область изменения случайной величины на интервалы шириной ∆х. Пронумеруем эти интервалы от нижней до верхней границы числами натурального ряда от 1 до k. Пусть вероятности попадания в каждый интервал равны соответственно ![]() . Введем энтропийные параметры непрерывного распределения следующим образом:
. Введем энтропийные параметры непрерывного распределения следующим образом:
 (5)
(5)
Чем меньше ширина интервалов Dх, тем точнее равенства в формуле (5).
Эмпирическая энтропия непрерывных распределений, прошедших процедуру дискретизации, найденная по результатам опытов, имеет нормальное распределение с параметрами, вычисленными по формулам (3), (4) с учетом (5).
Помимо вышеуказанного свойства эмпирической энтропии, что позволяет ввести новый критерий идентификации вида закона распределения [11], методы теории информации дают возможность построения адекватных моделей нелинейных процессов.
Рассмотрим двумерную случайную величину Z=(X,Y). Пусть Х - входной параметр, а Y– выходной параметр. Дискретизируем области изменения одномерных случайных величин X и Y. Пусть pxi (i=1…k1) – вероятности попадания значений случайной величины Х в соответствующие интервалы, а pyj (j=1…k2) – то же для Y. Обозначим через pij вероятность попадания случайной величины Z в соответствующую клетку.
Вычислим энтропии всех трех величин:
 (6)
(6)
Количество информации, передаваемое от входного параметра X выходному параметру Y, равно
![]() (7)
(7)
Можно показать, что в случае статистической независимости случайных величин X и Y энтропия двумерной величины Z равна сумме энтропий одномерных величин, а в случае детерминированной монотонной зависимости одномерных величин все три энтропии равны. На основании этого можно ввести параметр «коэффициент информационной связи»
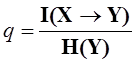 , (8)
, (8)
который равен нулю при статистической независимости одномерных величин и равен единице при детерминированной монотонной связи.
В работах F. Attneave [12] и A. von Eye [13] показано, что эмпирическая информация I*(X→Y) с точностью до постоянного множителя имеет χ2-распределение:
![]() (9)
(9)
Здесь m = (k1-1)(k2-1) - количество степеней свободы; k1, k2 - количество интервалов разбиения входного и выходного параметров соответственно; n - объем выборки.
Информация, передаваемая от одного параметра к другому, считается значимой, если
![]() , (10)
, (10)
где χ2m,α – α-квантиль χ2m-распределения; α – доверительная вероятность.
В этом случае считается также значимым и коэффициент информационной связи q*.
Пример построения информационной модели
По данным исследования зависимости производительности труда (Y) от заработной платы (X) (в процентах от базовой величины) получены следующие данные (табл. 1).
Таблица 1.
№ | Х | Y | № | X | Y | № | X | Y | № | X | Y | № | X | Y |
1 | 134 | 109 | 21 | 147 | 112 | 41 | 102 | 69 | 61 | 146 | 113 | 81 | 127 | 116 |
2 | 136 | 116 | 22 | 180 | 140 | 42 | 132 | 108 | 62 | 154 | 102 | 82 | 101 | 75 |
3 | 148 | 102 | 23 | 125 | 108 | 43 | 131 | 97 | 63 | 176 | 138 | 83 | 153 | 122 |
4 | 127 | 98 | 24 | 113 | 80 | 44 | 122 | 98 | 64 | 128 | 106 | 84 | 111 | 89 |
5 | 133 | 87 | 25 | 124 | 84 | 45 | 139 | 99 | 65 | 116 | 81 | 85 | 152 | 107 |
6 | 121 | 95 | 26 | 116 | 84 | 46 | 147 | 117 | 66 | 110 | 83 | 86 | 154 | 107 |
7 | 155 | 106 | 27 | 147 | 113 | 47 | 121 | 92 | 67 | 124 | 96 | 87 | 129 | 101 |
8 | 104 | 69 | 28 | 159 | 107 | 48 | 122 | 97 | 68 | 103 | 85 | 88 | 156 | 115 |
9 | 146 | 106 | 29 | 110 | 83 | 49 | 136 | 108 | 69 | 166 | 119 | 89 | 143 | 114 |
10 | 158 | 115 | 30 | 101 | 72 | 50 | 136 | 100 | 70 | 173 | 137 | 90 | 120 | 88 |
11 | 154 | 116 | 31 | 132 | 109 | 51 | 133 | 84 | 71 | 124 | 86 | 91 | 117 | 89 |
12 | 166 | 131 | 32 | 107 | 85 | 52 | 105 | 76 | 72 | 122 | 92 | 92 | 128 | 98 |
13 | 101 | 73 | 33 | 106 | 92 | 53 | 135 | 103 | 73 | 118 | 99 | 93 | 139 | 105 |
14 | 129 | 94 | 34 | 152 | 117 | 54 | 133 | 104 | 74 | 159 | 128 | 94 | 148 | 110 |
15 | 102 | 86 | 35 | 124 | 100 | 55 | 111 | 8n | 75 | 161 | 119 | 95 | 146 | 104 |
16 | 119 | 94 | 36 | 120 | 82 | 56 | 116 | 90 | 76 | 172 | 144 | 96 | 156 | 113 |
17 | 156 | 114 | 37 | 126 | 90 | 57 | 140 | 109 | 77 | 139 | 105 | 97 | 101 | 76 |
18 | 150 | 121 | 38 | 127 | 106 | 58 | 159 | 139 | 78 | 125 | 94 | 98 | 129 | 95 |
19 | 177 | 145 | 39 | 150 | 130 | 59 | 162 | 143 | 79 | 114 | 101 | 99 | 102 | 86 |
20 | 147 | 111 | 40 | 114 | 94 | 60 | 115 | 90 | 80 | 120 | 95 | 100 | 119 | 94 |
Первый шаг – построение диаграммы рассеивания (рис. 1).
На рис. 1 по горизонтали отложены значения фактора X, а по вертикали – признака Y. Визуальный анализ дает основание утверждать, что нет аномальных наблюдений, все точки не сильно удалены от других.
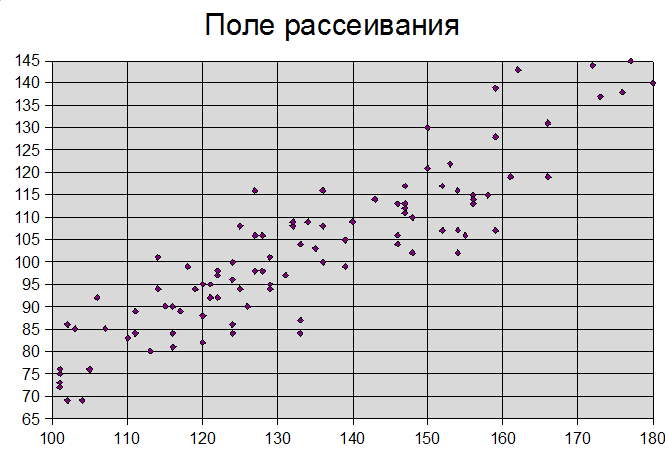
Рис. 1. Поле рассеивания экспериментальных наблюдений зависимости производительности труда (Y) от заработной платы (X) (в процентах от базовой величины).
Первый шаг. Строим двумерную гистограмму. Для этого разбиваем области изменения фактора Х и признака Y на интервалы, ширина которых близка к среднему квадратическому отклонению.
В табл. 2 приведены основные статистические характеристики исследуемых случайных величин.
В табл. 3 приведены частоты попадания значений двумерной случайной величины в соответствующие интервалы.
Таблица 2
Основные статистические характеристики
| Х | Y |
Среднее | 133,21 | 102,1 |
Стандартное отклонение | 20,27154 | 17,34062 |
Дисперсия выборки | 410,9353 | 300,697 |
Минимум | 101 | 69 |
Максимум | 180 | 145 |
Таблица 3.
Двумерная гистограмма.
Y | X | f(y) | |||
100-120 | 120-140 | 140-160 | 160-180 | ||
69-86 | 17 | 4 |
|
| 21 |
86-103 | 13 | 17 | 3 |
| 33 |
103-120 |
| 12 | 20 | 2 | 34 |
120-137 |
|
| 5 | 2 | 7 |
137-145 |
|
|
| 5 | 5 |
f(x) | 30 | 33 | 28 | 9 |
|
Второй шаг. Вычисляем энтропии H(X), H(Y), H(X,Y).
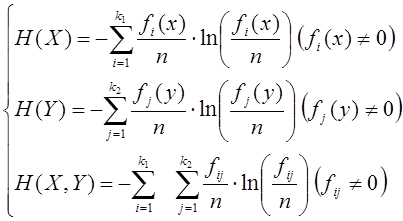
В результате расчетов получаем:
H(X)=1,300196; H(Y)=1,396325; H(X,Y)=2,134019.
Взаимная информация равна I(X→Y)=H(X)+H(Y)-H(X,Y)=0,562502.
Коэффициент информационной связи равен
q(X→Y)= I(X→Y)/H(Y)=0,402844.
Третий шаг. Оценка значимости найденной связи.
Значимость связи оценивается по критерию Пирсона χ2.
Взаимная информация с точностью до множителя 2n имеет распределение Пирсона: ![]() , где k1 – число интервалов разбиения области изменения случайной величины X, а k2 – число интервалов разбиения области изменения случайной величины Y. В нашем случае k1=4, k2=5.
, где k1 – число интервалов разбиения области изменения случайной величины X, а k2 – число интервалов разбиения области изменения случайной величины Y. В нашем случае k1=4, k2=5.
Итак, расчетное значение критерия Пирсона равно ![]() .
.
Табличное значение при числе степеней свободы m=(4-1)×(5-1)=12 и доверительной вероятности α=0,95 равно ![]() .
.
Т.к. расчетное значение критерия Пирсона больше табличного, то связь между признаком Y и фактором Х значима.
Заключение
Таким образом, в статье обоснована возможность использования статистики «энтропия» для решения разнообразных задач эконометрики.
В дальнейших публикациях автора предполагается рассмотреть информационный критерий идентификации вида закона распределения, проблемы построения и анализа информационных моделей, решение задач дискриминации и идентификации.
Список литературы
1. Башарин Г.П. О статистической оценке энтропии независимых случайных величин // Теория вероятностей и ее применения. 1956. Т. IV, № 3. С. 361-364
2. Бурлачков В. Экономическая наука и эконофизика: главные темы диалога // Вопросы экономики. 2007. № 12. С. 111-122.
3. Винер Н. Кибернетика, или управление и связь в животном и машине : пер. с англ. М.: Наука, 1983. 340 с.
4. Глущенко В.В. Использование спирали развития в виде n - кратно циклической би-спирали информации в борьбе с энтропией и хаосом в системных исследованиях экономики и управления // Управление экономическими системами. 2011. № 12. Режим доступа: http://uecs.ru/uecs-36-122011/item/852--n- (дата обращения 12.12.2012).
5. Кульбак С. Теория информации и статистика. М.: Наука, 1967. 408 с.
6. Мартин Н., Ингленд Дж. Математическая теория энтропии. М.: Мир, 1988. 350 с.
7. Петров Б.Н., Петров В.В., Уланов Г.М., Агеев В.М., Запорожец А.В., Усков А.В., Кочубиевский И.Д. Начала информационной теории управления // Техническая кибернетика. 1970. № 3. С. 10-14.
8. Райбман Н.С., Чадеев В.М. Построение моделей процессов производства. М.: Энергия, 1975. 376 с.
9. Хайтун С.Д. Социальная революция, энтропия и рынок // Общественные науки и современность. 2000. № 6. С. 94-109.
10. Шеннон К. Работы по теории информации и кибернетике : сб. статей : пер. с англ. М.: Иностранная литература, 1963. 829 с.
11. Юдин С.В. Информационный анализ // Известия Тульского государственного университета. Сер. Математика. Механика. Информатика. 1995. Т. 1, вып. 3. С. 136-145.
12. Attneave F. Information theory in der Psychologie. 2 Aufl. Bern, Stuttgart, Wienn. 1991.
13. Eye A. von. On the Equivalence of the Information-Theoretic Transmission-Measure to the Common 7c 52 0-Statistic // Biom. J. 1982. Vol. 24. P. 391-398.
14. Jaynes E.T. How Should We Use Entropy In Economics? St. John’s College, Cambridge. Available at: http://bayes.wustl.edu/etj/articles/entropy.in.economics.pdf , accessed 12.12.2012.
15. Kümmel Reiner. The Second Law of Economics: Energy, Entropy, and the Origins of Wealth. New York: Springer, 2011. 293 p.
Публикации с ключевыми словами: моделирование, анализ, теория информации, энтропия, эконометрика
Публикации со словами: моделирование, анализ, теория информации, энтропия, эконометрика
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



