научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#3 Март 2005
Норенков И.П. д-р техн. наук проф., Трудоношнв В.А. канд. техн. наук доцент, Федорук В.Г. канд. техн. наук доцент, МГТУ им. Н.Э.Баумана Обсуждаются вопросы многоаспектного моделирования мехатронных устройств. Приведены результаты расчета объектов, содержащих подсистемы различной природы. Целью статьи является рассмотрение подхода к анализу на ЭВМ мехатронных устройств. При этом под мехатронными устройствами понимаются объекты, для исследования и проектирования которых используются математические модели, отражающие взаимное влияние протекающих в объекте процессов различной физической природы. Рассмотрение ведется на макроуровне, т.е. при дискретизации пространственных величин, что приводит к моделям в виде систем обыкновенных дифференциальных уравнений. В то же время описываемый подход отличается от принятого в теории автоматического управления тем, что в математических моделях используются не абстрактные сигналы, а величины, непосредственно характеризующие физическое состояние объекта (токи, потенциалы, давления, силы и т.п.) и связанные компонентными уравнениями. В современных системах автоматизированного проектирования (САПР) для анализа на макроуровне, как правило, применяются программы одноаспектного (монодисциплинарного) моделирования. Определились программы - мировые лидеры - для анализа электронных схем (Spice) и механических устройств (Adams, Dyna). Так, в программах типа Spice в качестве фазовых переменных используются электрические токи и напряжения. Хотя влияние температуры на электрические процессы можно учесть путем введения в модели компонентов температурных зависимостей параметров, такой учет является все же односторонним. В Spice-подобных программах обратное влияние электрических переменных на тепловой режим не предусматривается и, следовательно, отсутствуют возможности учета двустороннего (взаимного) влияния фазовых переменных тепловой и электрической подсистем. Аналогичная ситуация имеет место и в отношении других физических подсистем и известных программ анализа. Математический аппарат анализа, разработанный для одноаспектного моделирования, входит составной частью в методики анализа мехатронных устройств. Однако требуются и развивающие дополнения, приводящие к инвариантности форм представления моделей разных физических объектов и, следовательно, к объединению моделей и их решению в едином вычислительном процессе. Прежде всего к таким дополнениям нужно отнести аналогии фазовых переменных, компонентных и топологических уравнений, в достаточной мере описанные в литературе [1, 2]. Разработаны методики построения эквивалентных схем, являющиеся основой для многоаспектных моделей [3]. Однако до настоящего времени методики многоаспектного моделирования почти не используются в существующих САПР, хотя в средствах анализа систем с физически разнородными подсистемами нуждается большинство проектных организаций приборостроительного профиля. Вначале статьи кратко изложены основы единообразного построения эквивалентных схем объектов в разных приложениях, далее рассмотрены вопросы построения математических моделей взаимодействия подсистем различной физической природы и проиллюстрированы возможности многоаспектного моделирования на примерах конкретных мехатронных устройств. Эквивалентные схемы мехатронных устройств. Наличие аналогий фаэовых переменных и уравнений в разных приложениях позволяет создать единое математическое и программное обеспечение для САПР объектов мехатроники. Выделяются два типа уравнений, составляющих математические модели (ММ): уравнения, описывающие состояния элементов, так называемые компонентные, и уравнения, зависящие от конфигурации подсистемы, от способов соединения элементов друг с другом, так называемые топологические. Фазовые переменные, фигурирующие в этих уравнениях, также можно разделить на два типа: переменные типа потенциала и типа потока. Переменные типа потенциала 'соответствуют местам соединения (узлам, полюсам) элементов, переменные типа потока соответствуют двухполюсным элементам, представляемым в схемах в виде ветвей. Выбор фазовых переменных для подсистем неоднозначен, так, например, для механической подсистемы в качестве фазовых переменных типа потенциала может быть выбрана либо скорость либо перемещение. Предлагаемый в таблице набор фазовых переменных нашел практическое применение в известной программе анализа ПА7 [4]. Аналогии топологических уравнений выражаются в уравнениях равновесия и непрерывности. Уравнения равновесия для перечисленных в таблице подсистем имеют вид: åXi=0, (1) iÎq где Х1 — переменная типа потока, т.е. принадлежащая множеству {F, М, I, О, Ф}, q — множество номеров ветвей, инцидентных i-му узлу. Уравнения непрерывности выглядят так: åYj=0, (2) jÎp
где У, — переменная типа потенциала, т.е. принадлежащая множеству (V, w, U, Р, T), р — множество номеров ветвей, входящих в j-й контур. В различных предметных областях эти уравнения носят разные названия, так, например, в механике — это принцип Даламбера и принцип сложения скоростей, в электронике — первый и второй законы Кирхгофа. Важно, что формы
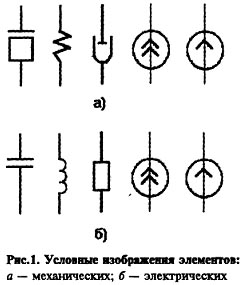 представления уравнений в разных приложениях идентичны. Это обстоятельство приводит к идентичности методик составления эквивалентных схем разных подсистем, объединяемых далее в общую исследуемую схему. Составление эквивалентных схем выполняется следующим образом. Сначала разработчик определяет существенные, с его точки зрения, эффекты, влияющие на состояние объекта. Сначала разработчикопределяет существенныес его точки зрения,эффекты,влияющие насостояние объекта. Затем выбирается базовый узел эквивалентной схемы. Для механической поступательной подсистемы базовый узел соответствует инерциальной системе отсчета, в электрической подсистеме — это корпус прибора. Далее выбранные эффекты моделируются включением тех или иных элементов в схему. Так, в механической поступательной подсистеме инерционные свойства тел определяются элементами массы, одним полюсом подключаемыми к базовому узлу, другим полюсом — к узлу, изображающему тело с инерционной массой. Упругие свойства представляются элементами упругости, подключаемыми к узлам, соединенным упругой связью. Диссипативные потери учитываются элементами потерь, подключаемыми к контактирующим узлам. Воздействия на механическую поступательную подсистему могут изображаться с помощью источника силы и источника скорости. Условные изображения перечисленных элементов показаны на рис. 1,а. Аналогичным образом строятся эквивалентные схемы механических вращательных подсистем. Способы построения эквивалентных схем электрических и гидравлических подсистем не отличаются от традиционных методик, в которых используются условные изображения элементов емкости, индуктивности, сопротивления, источников тока и напряжения, показанные на рис. 1,б Типы элементов и способы их соединения друг с другом, выражаемые эквивалентной схемой, дополненные численными значениями параметров элементов, составляют сведения, достаточные для получения систем алгебро-дифференциальных уравнений, описывающих поведение исследуемого объекта. Разработано большое количество методов формирования ММ, каждому из которых присущи свои достоинства и недостатки, но их обзор выходит за рамки этой статьи. Пример обобщенного метода формирования математических моделей объектов приведен в [5]. Для алгебраизации получающихся систем уравнений чаще других используется модифицированный метод трапеций, для их линеаризации — метод Ньютона, и для решения систем линейных алгебраических уравнений — разновидности метода Гаусса. Модели взаимодействия подсистем различной физической природы. На рис.2,а и рис.2б представлены поступательная и вращательная подсистемы, с их эквивалентными схемами. Оба объекта состоят из двух взаимодействующих подсистем, эквивалентная схема каждой из которых составлена в соответствии с изложенными выше алгоритмами. Теперь рассмотрим элементы, определяющие взаимодействие между подсистемами. В поступательных подсистемах к ним относятся элементыF1,V2,D1 и D2. В зоне взаимодействия двух подсистем можно записать уравнения взаимосвязи фазовых переменных: F1 = k Fv2, V2 = k V1, k = tg a, где F1 — силовое воздействие на массу тг со стороны массы m2; Fv2 — силовое воздействие на массу т2 со стороны m1 V1 — поступательная скорость массы т1; V2 — поступательная скорость массы т2 Поскольку сила трения зависит от нормальной силы, то для элементов D1 и D2 можно в простейшем случае использовать следующие компонентные уравнения: Fd1=kтрFv2, Fd2=kтрF1. При составлении эквивалентной схемы и записи компонентных уравнений предполагалось, что т1 и т2 всегда находятся в соприкосновении друг с другом, хотя возможен учет разрыва контакта при некотором усложнении эквивалентной схемы и компонентных уравнений элементов взаимосвязи. Для механической вращательной подсистемы элементами, определяющими взаимодействие между элементами J1 и J2 являются M1, w2 и D5. С помощью D5 учитывается проскальзывание ремня по шкивам, М1 = k2Мw2, где Мw2 — момент, воздействующий на J2 со стороны J1 w2 — источник угловой скорости, воздействующий на J2, с уравнением w2 = k2 w1 где w1 — угловая скорость элемента J1 Составление эквивалентных схем для подсистем другой физической природы также формализовано и рассмотрено в литературе [1, 3]. Особенностью получения ММ с помощью эквивалентных схем является то, что внимание при этом
сосредоточивается на компонентных уравнениях элементов, которые могут быть реализованы с нелиней-ностями практически любого типа, причем, поскольку каждое компонентное уравнение при программном исполнении реализуется в подпрограмме, то оно может содержать и логические зависимости.
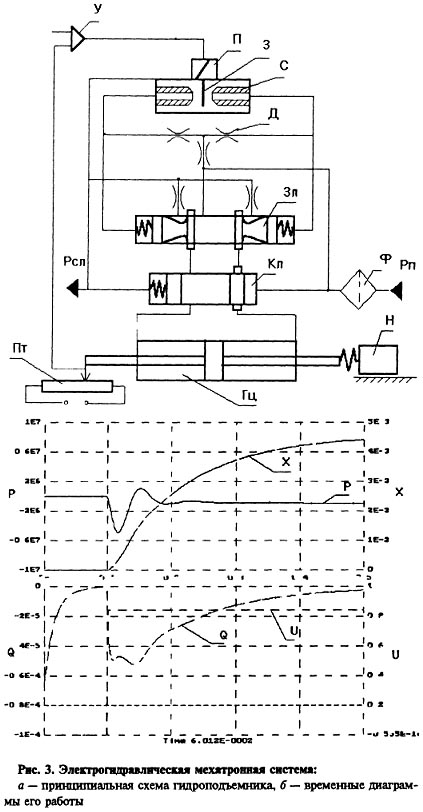
Современные программные комплексы анализа и верификации строятся таким образом, что допускают при разработке ММ использование вложенных моделей, что существенно облегчает этот процесс и, кроме того, этап составления эквивалентных схем становится характерным только при разработке моделей низшего уровня. На более высоких уровнях для пользователей предлагаются более привычные им элементы, например для механики, это может быть редуктор, дифференциал, для гидромеханики — гидролиния, гидроцилиндр и т.п.Примеры анализа динамики конкретных объектов. На рис 3,д приведена принципиальная схема электрогидравлического следящего привода. Здесь: У — усилитель; П — электромеханический преобразователь; 3 — заслонка, С — сопло; Д — дроссели; Зл — золотник; Ф — фильтр, Пт — потенциометр; Гц — гидроцилиндр; Н — нагрузка. Привод работает следующим образом: при изменении сигнала управления возникает ток рассогласования; электромеханический преобразователь перемещает заслонку; зазор между одним соплом и заслонкой увеличивается, между другим уменьшается; из-за возникшей разности давлений смещается золотник; одна из полостей гидроцилиндра подключается к питающей магистрали, другая — к сливу; перемещение поршня гидроцилиндра приводит к смещению нагрузки, одновременно пропорционально смещению изменяется сигнал, снимаемый с потенциометра обратной связи, при нулевом рассогласовании заслонка занимает среднее положение и движение поршня гидроцилиндра прекращается. Таким образом обеспечивается слежение выходного звена гидропривода за сигналом управления. Устройства подобного типа используются в качестве исполнительных устройств автоматических систем управления летательными аппаратами.
На рис. 3,6 представлены временные диаграммы работы привода, полученные с помощью программного комплекса SIMHYD. Здесь X — перемещение штока гидроцилиндра; (3 — расход рабочей жидкости, поступающей в гидроцилиндр; II — управляющее воздействие; Р — перепад давления в полостях гидроцилиндра. По полученным результатам можно оценить быстродействие привода при ступенчатом изменении сигнала управления, а выполнив несколько вариантов расчета с различными параметрами элементов, выбрать лучший из них.
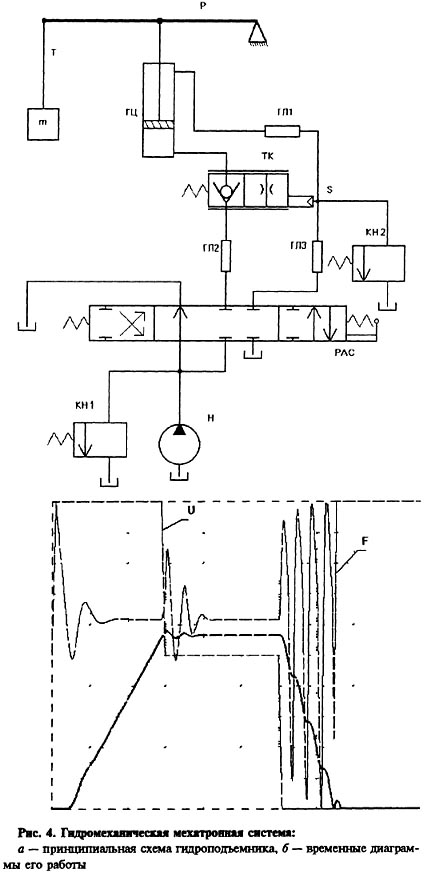
На рис. 4,я изображена принципиальная схема гидроподъемника для перемещения грузов в вертикальном направлении. Обозначения элементов следующие: т — поднимаемый (опускаемый) груз; Т — трос; Р — стрела (рычаг) гидроподъемника; ГЦ — двусторонний гидроцилиндр; ТК — тормозной клапан, состоящий из обратного клапана и нелинейного дросселя, проводимость которого зависит от давления в точке 8; РАС — трехлинейный трехпозиционный распределитель; КН1, КН2 — напорные клапаны; Н — насос; ГЛ1 — ГЛЗ — гидролинии.
Подъемник работает следующим образом: для подъема груза распределитель смещается влево (по схеме) при этом жидкость от насоса через ГЛ2 и обратный клапан тормозного клапана будет поступать в нижнюю (по схеме) полость гидроцилиндра, перемещая его поршень, и, соответственно, через рычаг поднимать груз; из верхней полости гидроцилиндра жидкость через ГЛ1, ГЛЗ и распределитель будет сливаться в бак; при смещении распределителя в центральное положение каналы для движения жидкости из обоих полостей закрываются и поршень останавливается в текущем положении, фиксируя груз; для опускания груза распределитель смещается вправо, жидкость от насоса через распределитель, ГЛЗ, ГЛ1 поступает в верхнюю полость гидроцилиндра, из нижней полости через нелинейный дроссель тормозного клапана (обратный при этом закрыт), ГЛ2 и распределитель жидкость сливается в бак. Назначение напорного клапана КН2 — ограничить в режиме опускания давление в верхней полости гидроцилиндра и, соответственно, скорость опускания груза.
На рис.4,6 показаны временные диаграммы работы гидроподъемника в режимах поднятия и опускания груза, полученные с помощью программного комплекса ПА7. Здесь Р — усилие на тросе; II — управляющее воздействие; X — перемещение груза. Параметры напорного клапана КН2 соответствуют случаю натурных испытаний, в которых происходило раскачивание груза в режиме опускания, что и подтвердили результаты моделирования В результате с помощью моделирования удалось подобрать параметры КН2 для плавного опускания груза.
Использование излагаемых в статье методов и средств мехатроники позволяет существенным образом сократить временные и материальные затраты на проектирование сложных технических устройств.
Интерес к методам и средствам анализа мехатронных устройств за рубежом заметно возрос в последние два-три года, о чем свидетельствует хотя бы работа [6] и организация в 1995 г. международной конференции ССRАМ'95, посвященной проблемам развития мехатроники. Разработанные в нашей стране методики автоматизированного анализа технических объектов на макроуровне позволяют непосредственно приступить к их реализации в промышленных системах автоматизированного проектирования мехатронных устройств. Приведенные примеры моделирования иллюстрируют возможности исследования функционирования сложных систем с учетом взаимного влияния разнородных физических процессов.
Литература
1. Снгорскнй В.П. Математический аппарат инженера — Киек Техиха, 2. Норенков И.П. Введение в автоматизированное проектирование 3. Трудоношин ВА., Пивоваров* Н.В. САПР. Математические модели 4. ТгаДоповЫп УЛ., РеДогик У.С. АрргоасЬез ю МаШетаИса! 'МоЛЖ 5. Норенков И.П., Трудоношнн ВА., Федорук В.Г. Метод формирования 6. СотеНоп! К. Меспа...^па1? [тесЬа1гогас5]/8ресШ1т, Аи& 1994. Р.46-49.
| ||||||||||||||||||||
Публикации с ключевыми словами: анализ, САПР, макроуровень
Публикации со словами: анализ, САПР, макроуровень
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||