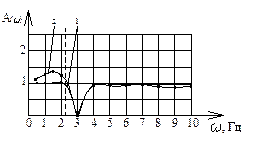научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 05, май 2012
DOI: 10.7463/0512.0378353
УДК 621.534.833.886.6
Россия, НИИ современных технологий, системного анализа и моделирования,
Россия, Иркутский государственный университет путей сообщения
Введение. Задачи виброзащиты и виброизоляции, рассматриваемые в динамике машин, связаны, чаще всего, с поиском и разработкой средств управления динамическим состоянием некоторого объекта, который подвержен действию внешних факторов различной природы. Управление динамическим состоянием, в широком смысле, определяется не только представлениями о возможном выборе рациональных параметров механических колебательных систем, состоящих из некоторого набора элементарных звеньев, но и использованием специальных устройств, реализующих желаемые динамические эффекты. Вибрационная защита машин и оборудования пересекается с задачами таких направлений науки и техники как робототехника, мехатроника, вибрационная диагностика, транспортная динамика и др., поскольку общим является поиск способов и средств управления динамическим состоянием систем [1, 2].
Хотя вопросам реализации способов и средств динамического гашения в течении последних лет уделялось достаточно большое внимание, как со стороны отечественных, так и зарубежных специалистов, многие вопросы не получили должного освещения. Имеются проблемы, связанные с расширением самого понятия динамического гашения колебаний и способах его конструктивно-технических реализаций, учетом влияния таких факторов как сочленения звеньев и др. Динамические гасители колебаний используются как отдельное или автономное направление в технике виброзащиты в тех ситуациях, когда необходимо снизить уровень динамических воздействий при известных, как правило гармонических, воздействиях. В последнее время наметились новые подходы в рассмотрении комбинационных режимов движения в системах с несколькими степенями свободы, когда выделяются определенные формы движения, совместные по нескольким координатам. Одним из направлений изучения режимов динамического гашения становится систематическое развитие идей введения дополнительных динамических связей, реализуемых в достаточно сложных формах, таких, как механические колебательные структуры и механизмы [3].
I. Основы подхода.При всем разнообразии способов и средств, поиске и разработке новых технических решений наиболее распространенными являются методы, основанные на выделении задач, трактующих идею динамического гашения, как присоединение дополнительной массы с помощью упругого элемента [4]. Вместе с тем, достаточно широко известны результаты, связанные с другими формами динамического гашения колебаний, основанные на использовании маятниковых устройств, рычажных механизмов, устройств для преобразования движения, дополнительных вращений звеньев, создающих центробежные силы; известны также технологии уравновешивания и балансировки вращающихся масс [1]. В обобщенном представлении динамическое гашение можно рассматривать и как введение дополнительных связей в интерпретациях, допускаемых теорией автоматического управления (рис. 1 а, б).

Рис. 1. Схема, отражающая введение дополнительной связи:
а) на уровне конструктивно-технических форм; б) структурные интерпретации
Основным недостатком динамического гашения колебаний является сложность их настройки на внешние воздействия, которые обладают нестационарными параметрами. Проблемы возникают и с учетом влияния сил сопротивления, ограничивающих эффективность динамического гашения колебаний в целом. Подход, в рамках которого динамическим аналогом линейной механической колебательной системы становится система автоматического управления, связан с расширением представлений о наборе типовых элементарных звеньев виброзащитных системы, что приводит к разработке технологии соединения типовых элементарных звеньев для получения более сложных структур. Серьезное развитие идеи динамического гашения колебаний получили в работах по балансировке и уравновешиванию вращающих масс, что предопределило появление систем автоматической настройки. Интерес к возможностям построения активных систем управления колебательными процессами в механических системах способствовал развитию мехатроники, как междисциплинарного научного направления в задачах динамики машин. Возможности динамических гасителей колебаний, например, частоты режимов динамического гашения определяются частотным уравнением числителя передаточной функции системы [1]. Рассмотрим особенности выделения и описания обратных связей (Рис. 2 а-е) в механических колебательных системах. В развитие концепции обратной связи предлагается подход к системному рассмотрению основных этапов формирования математических моделей.
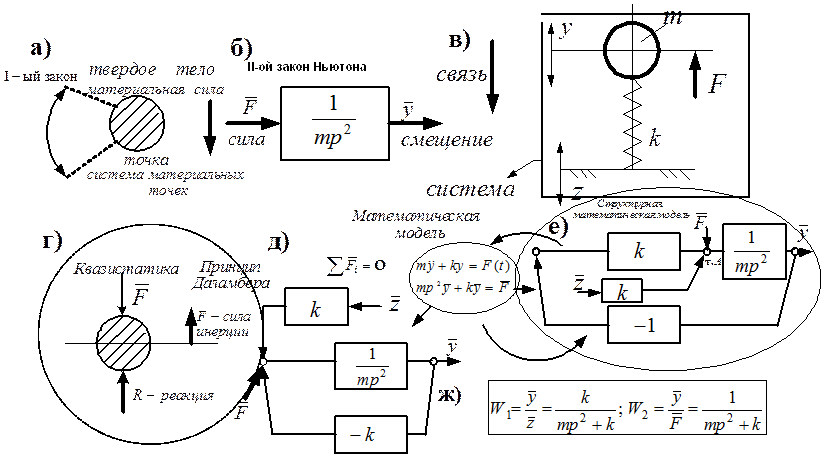
Рис. 2. Принципиальная схема связи понятий в концепции обратной связи
Отметим, что структурные представления (Рис. 2 е) делают равнозначными силовые и кинематические внешние воздействия; это послужило основой развития представлений об обобщенных задачах виброзащиты и виброизоляции. Структурная схема на рис. 2 е может быть названа базовой схемой механических колебательных систем, в том смысле, что более сложные системы могут быть построены путем усложнения базовой системы через введение дополнительных связей или соединения нескольких блоков между собой. Для описания связи между выходными и входными величинам используются передаточные функции. На рис. 2 ж показаны, соответственно, W1 (p) – передаточная функция «смещение объекта массой m – смещение основания z» и W2 (p) – «смещение объекта массой m – внешняя сила F». В простейшей механической колебательной системе (Рис. 3 а), состоящей из двух элементов массами m1 и m2, соединение обеспечивается упругой связью в виде пружины с жесткостью k. В точке А (Рис. 3 б) приложена внешняя сила F; y1 и y2 - координаты смещения масс. Система состоит из двух парциальных систем I и II, отмеченных соответствующими контурами на рис. 3 б. Математическая модель системы приведена на рис. 3 в и представляет собой систему двух дифференциальных уравнений 2-ого порядка. На позиции рис. 3 г приведены передаточные функции W1 (p) и W2 (p), которые позволяю найти частоту собственных колебаний (выражение – (1)) и частоту динамического гашения (выражение (2)). Важным для дальнейшего рассмотрения является то обстоятельство, что парциальные системы I и II имеют перекрестные связи, представленные на структурной схеме (Рис. 3 б) двумя каналами взаимодействия со звеном усиления k. Структурная схема (Рис. 3 б) позволяет путем формальных преобразований построить структурную модель, отражающую такой вид динамического воздействия, как динамическое гашение колебаний при действии внешней возмущающей моногармонической силы F. Режим динамического гашения при расчетной схеме, представленной на рис. 3 а, соответствует введению в структурной схеме (Рис. 3 б) положительной обратной связи. В целом, общая схема (Рис. 3 а-е) динамических взаимодействий в системе свободного движения двух соединенных упругой связью k масс m1 и m2 дает представление о формировании связей и их функциональном назначении [4].
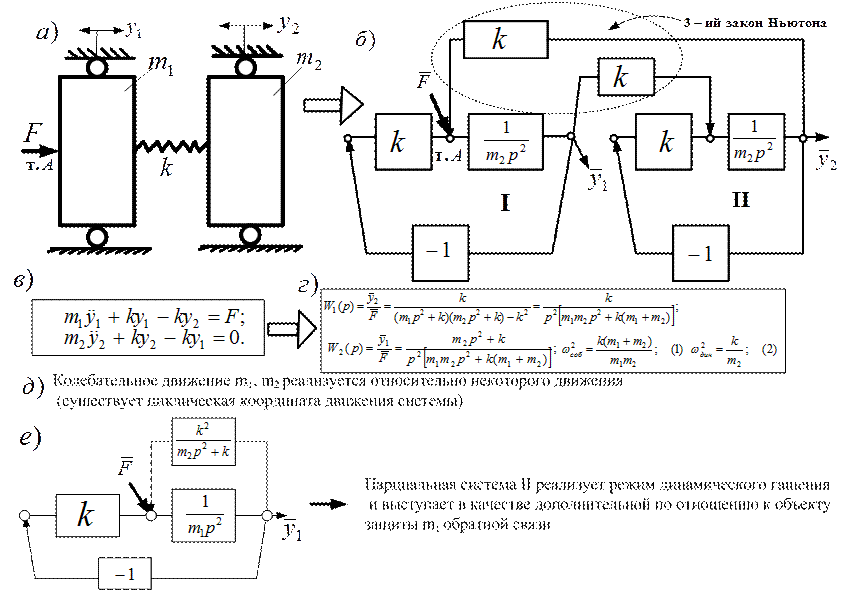
Рис. 3. Общая схема динамического взаимодействия в двухмассовой системе
Структурный подход, развиваемый в статье, предопределяет использование передаточной функции в качестве основной динамической характеристики механических колебательных систем и виброзащитных систем, в частности. Введение понятия о расширенном наборе элементарных типовых звеньев механических колебательных систем позволяет изменять структуры базовых моделей исходной системы; при этом происходит формирование дополнительных обратных связей в виде механических цепей той или иной сложности. В такой интерпретации дополнительная обратная связь может рассматриваться как обобщенная пружина (или квазипружина) и иметь передаточную функцию в виде дробно-рационального выражения. В работе [1] приводятся некоторые примеры реализации дополнительных обратных связей для различных систем.
Присоединение дополнительных масс с целью построения в системе координат, связанной с неподвижной системой отсчета, динамического гасителя колебаний на несколько частот внешних кинематических воздействий, приводит к увеличению значений частоты собственных колебаний парциальной системы, содержащей объект защиты.
II. Динамическое гашение колебаний как введение обратных связей. Виброзащитная система с использованием динамического гашения колебаний может состоять из нескольких элементов. На рис. 4 показано несколько расчетных схем, которые можно разделить на 4 группы:
- динамические гасители имеют связи между массами ![]() и
и ![]() , но элемент массой
, но элемент массой ![]() не имеет связи (
не имеет связи (![]() ) с объектом защиты
) с объектом защиты ![]() (Рис. 4 а);
(Рис. 4 а);
- динамических гасителей два, при этом ![]() и
и ![]() связаны с объектом защиты
связаны с объектом защиты ![]() , но не связаны между собой (
, но не связаны между собой (![]() ) (Рис. 4 б);
) (Рис. 4 б);
- дополнительные массы ![]() и
и ![]() связаны каждый с объектом защиты
связаны каждый с объектом защиты ![]() , но также
, но также ![]() и
и ![]() связаны между собой (
связаны между собой (![]() ), (Рис. 4 в);
), (Рис. 4 в);
- динамический гаситель представляет собой не две дополнительные массы ![]() и
и ![]() , а твердое тело, имеющее массу
, а твердое тело, имеющее массу ![]() и момент инерции
и момент инерции ![]() при упругих опорах
при упругих опорах ![]()
![]() (Рис. 4 г).
(Рис. 4 г).
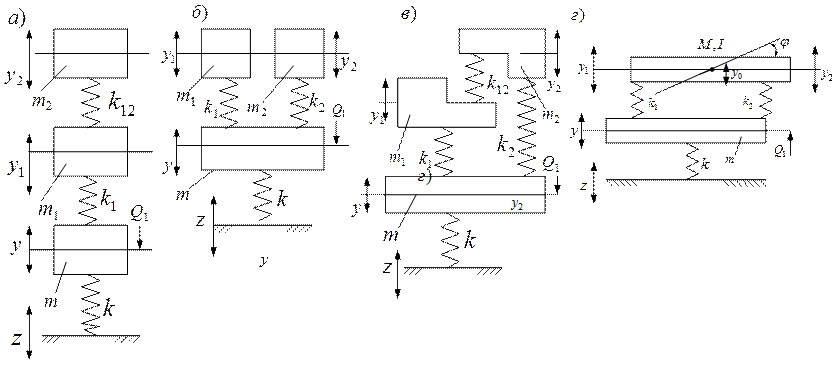
Рис. 4. Расчетные схемы виброзщитных систем с двумя динамическими гасителями колебаний
В качестве примера на рис. 5 приведена структурная схема динамического гасителя колебаний по схеме, соответствующей рис. 4 а. Динамические свойства системы (Рис. 5.) могут быть оценены из анализа структурной схемы: на частоте 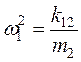 обратная связь «обнуляется», и объект защиты совершает независимые от динамических гасителей колебаний
обратная связь «обнуляется», и объект защиты совершает независимые от динамических гасителей колебаний ![]() и
и ![]() . В свою очередь, знаменатель передаточной функции цепи обратной связи представляет собой частотное уравнение вида
. В свою очередь, знаменатель передаточной функции цепи обратной связи представляет собой частотное уравнение вида
![]() (1)
(1)
Корни уравнения (1) определяют частоты динамического гашения
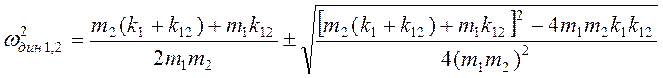 . (2)
. (2)

Рис. 5. Структурная схема системы с динамическим гасителем, состоящим их двух масс (![]() и
и ![]() )
)
Аналогичным образом могут быть рассмотрены расчетные схемы представленные на рис. 4 б и 4 в. Можно отметить, что по сравнению со схемой на рис. 4 а элемент k12 не дает возможности получить упрощения в такой форме как на рис. 4 б из-за наличия непланарных связей, а это требует использования специальных приемов. Учет связности в движениях динамических гасителей m1 и m2 изменяет параметры режима динамического гашения и других, но, в целом, динамические свойства системы остаются теми же, если иметь в виду число резонансов и число режимов динамического гашения.
Расчетная схема такого гасителя со связанными движениями представлена на рис. 4 г. Движение динамического гасителя рассмотрено в системе координат ![]() и
и ![]() , а также в системе координат
, а также в системе координат ![]() и
и ![]() , относящихся к центру тяжести твердого тела. Рассмотрим особенности выбора систем координат. На рис. 6 представлена расчетная схема динамического гасителя колебаний для твердого тела (модельная задача транспортной динамики) с рычажным динамическим гасителем колебаний.
, относящихся к центру тяжести твердого тела. Рассмотрим особенности выбора систем координат. На рис. 6 представлена расчетная схема динамического гасителя колебаний для твердого тела (модельная задача транспортной динамики) с рычажным динамическим гасителем колебаний.

Рис. 6. Расчетная схема системы с упрощенным ДГ и учетом смещения центра масс в т. A1
Решение задачи произведено с учетом изменения положения центра масс системы при установке гасителя. На рис. 7 показаны амплитудно-частотные характеристики (АЧХ); отметим, что семейство кривых, которые отражают влияние изменения смещения точки установки ДГ на свойства системы. Для системы характерно наличие двух режимов динамического гашения в до- и межрезонансных частотах области (рис. 7 а). На рис. 7 б взаимное расположение АЧХ показано более детализировано.
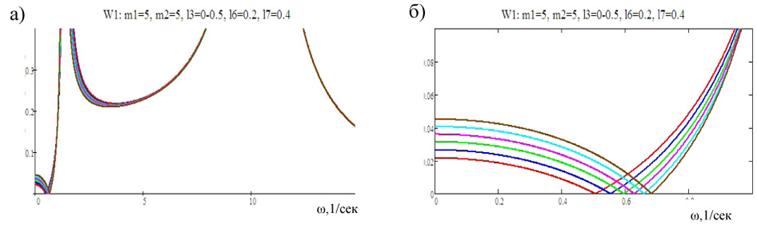
Рис. 7. Семейство АЧХ системы по координате у, при различных значениях l0 (а); взаимное расположение АЧХ в дорезонансной области (б)
Влияние изменения l0 на характер взаимного расположения АЧХ зависит, существенным образом, от соотношения параметров и выбора системы координат объекта защиты.
II. Некоторые приложения теории динамических гасителей. Разработка обобщенной методики математического моделирования динамического гашения колебаний и некоторым приложениям теории требуют определенных уточнений. Предлагаемая подвеска, точнее, ее модель, состоит (Рис. 8) из объекта защиты массой М с учетом моментов инерции I. Центр тяжести твердого тела расположен в т. А; в системе подвески задействованы два рычага с массами m1 m2; их моменты инерции относительно т. А обозначаются соответственно через I1 и I2. К такой расчетной схеме приводится, например, тележка с двумя тяговыми двигателями для электровоза.

Рис. 8. Расчетная схема тележки с инерционными рычагами
Система дифференциальных уравнений движения в системе координат ![]() имеет вид:
имеет вид:
 (3)
(3)
 (4)
(4)
В координатах ![]() и
и ![]() система уравнений (2), (3) преобразуется к другому виду, что позволяет искать соотношение параметров системы, обеспечивающее одновременно гашение по двум координатам. Выбор режима динамического гашения определяется условиями задачи вибрационной защиты и зависит от вида передаточной функции настроечного звена
система уравнений (2), (3) преобразуется к другому виду, что позволяет искать соотношение параметров системы, обеспечивающее одновременно гашение по двум координатам. Выбор режима динамического гашения определяется условиями задачи вибрационной защиты и зависит от вида передаточной функции настроечного звена ![]() . В качестве примера на рис. 9 а,б показаны возможности выбора свойств амплитудно-частотных характеристик (использовался пакет прикладных программ Mathcad).
. В качестве примера на рис. 9 а,б показаны возможности выбора свойств амплитудно-частотных характеристик (использовался пакет прикладных программ Mathcad).
а) б)


Рис. 9. Амплитудно-частотные характеристики системы по координате y:
а) два режима динамического гашения, б) режим динамического гашения до первого резонанса
Последовательная система возможных вариантов построения систем с динамическим гасителем рычажного типа приведены на рис. 10. Амплитудно-частотные характеристики, отражающие особенности динамических свойств, приведены на рис. 11 [5].
а) б)

в)
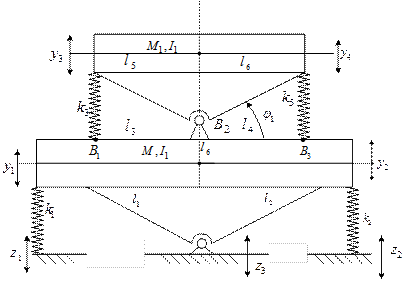
Рис. 10. Расчетная схема для виброзащитной системы с сочленениями:
а – соответствует сочленению ![]() ; б – соответствует сочленению
; б – соответствует сочленению ![]() ; в – соответствует сочленениям
; в – соответствует сочленениям ![]() и
и ![]() одновременно
одновременно

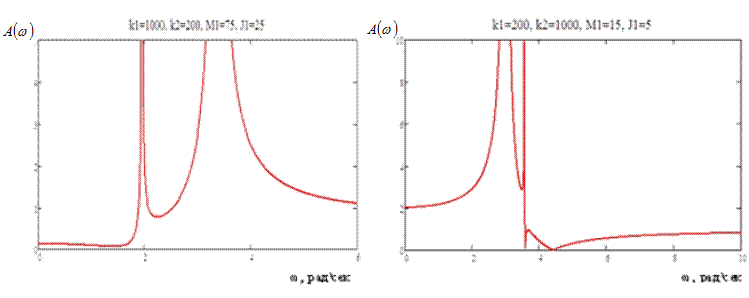
Рис. 11. Виды амплитудно-частотных характеристик системы при различных соотношениях параметров (значения параметров приведены на поле рисунка)
В качестве одного из приложений могут быть рассмотрены возможности динамического гасителя колебаний, получаемого на основе применения обобщенной методики построения математических моделей систем. Схемы, приведенные на рис. 12, связаны между собой возможностями преобразований на основе метода исключения переменных. Общий вид амплитудно-частотной характеристики системы с динамическим гасителем рычажного типа по рис. 12 а приведена на рис. 13.

Рис. 12. Расчетные схемы виброзащитных систем с рычажным динамическим гасителем колебаний: а) упругости рычага и шарниров не учитываются; б) учитываются упругости всех шарниров; в) учитываются упругости шарнира крепления с основаниеми упругость рычага
Передаточная функция виброзащитной системы по рис. 12 а имеет вид:
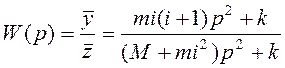 . (5)
. (5)
На рис. 14 приведена построенная на основе (5) Амплитудно-частотная характеристика (ачх), на которой показаны три характерных случая. При выполнении условия M = mi виброзащитная система запирается, а при M ≠ miреализуется один из вариантов амплиьудно-частотной характеристики.
Для рассмотрения особенностей динамического гашения в системах с рычажным связями проводился эксперимент на макете виброзащитной системы с устройством для преобразования движения. Общий вид экспериментальной установки приведен на рис. 14.
|
|
Рис. 13. Амплитудно-частотные характеристики системы при разных соотношениях масс: | Рис. 14. Общий вид экспериментального стенда,
|
Для проведения эксперимента использовался вибростенд марки С-004 (частотный диапазон 0.1-20 Гц), многоканальный синхронный комплект виброизмерительной аппаратуры «Атлант-8» (серийный номер №070), датчики для измерения вибраций – «Виконт» марки ВК-310А. На рис. 15 приведены характерные записи движения объекта в зонах дорезонансной, резонансной и зарезонансной областях. Амплитудно-частотные характеристики при различных значениях передаточного отношения приведены на рис. 16 а,б. Обработка результатов эксперимента проводилась на основе известной методики с применением среднеквадратичных значений измеряемых величины.
| а)
| б)
|
| Рис. 16. Амплитудно-частотные характеристики экспериментальной установки; а) при m=0,2 кг; б) m=0,7 кг | |
Наилучшее совпадение результатов наблюдалась в области низких частот (2-7 Гц). «Запирание» системы, характерное для высоких частот, дает совпадение результатов в пределах 12 %. При увеличении частот >20 Гц эксперимент искажается влиянием нелинейных факторов, связанных с искажением формы внешнего возмущающего сигнала. В целом можно полагать, что эксперимент дает удовлетворительное совпадение с теоретическими расчетами в плане определения возможностей реализации динамических эффектов в различных частотных диапазонах.
Заключение. На основе проведенных исследований предлагается метод построения математических моделей для систем вибрационной защиты, использующих динамические гасители колебаний с несколькими степенями свободы, заключающийся в том, что динамические гасители интерпретируются в виде дополнительных обратных связей. Результаты изучения свойств динамических гасителей колебаний различных конструктивно-технических вариантов позволяют расширить понятие режима динамического гашения и определить значение выбора систем обобщенных координат. Авторами предлагается и разработана методика преобразования структурных схем механических колебательных систем на основе их упрощения через сочленение звеньев, позволившая сформировать обоснование появления и использования в механических системах рычажных связей. Предложение методика оценки свойств механических колебательных систем в режимах динамического гашения колебаний одновременно по нескольким координатам движения объекта защиты.
Библиографический список
1. Елисеев С.В., Резник Ю.Н., Хоменко А.П. Мехатронные подходы в динамике механических систем. – Новосибирск.: Наука. – 2011. – 394 с.
2. Елисеев С.В., Резник Ю.Н., Хоменко А.П., Засядко А.А. Динамический синтез в обобщенных задачах виброзащиты и виброизоляции технических объектов. – Иркутск.: Ирк. гос. университет. – 2008. – 523 с.
3. Вибрации в технике: справочник в 6 т. Т. 6. Защита от вибраций и ударов / под ред. К.В. Фролова. – М.: Машиностроение. – 1981. – 456 с.
4. Елисеев С.В., Ермошенко Ю.В., Трофимов А.Н. К вопросу о построении математических моделей виброзащитных систем с динамическими гасителями колебаний нетрадиционного типа// Современные технологии. Системный анализ. Моделирование. Выпуск 2(30) – Иркутск 2011 с.78-83.
5. Елисеев С.В., Белокобыльский С.В. Обобщенные подходы к построению математических моделей механических систем с Г-образными динамическими гасителями колебаний. // Системы. Методы. Технологии. – № 1(9). – Братск.: БрГУ. – 2011. – с. 9 – 24.
Публикации с ключевыми словами: динамическое гашение колебаний, структурные преобразования математических моделей, обратная связь
Публикации со словами: динамическое гашение колебаний, структурные преобразования математических моделей, обратная связь
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||