научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2011
УДК 621.37: 621.38: 538.911
МГТУ им. Н.Э. Баумана
Сканирующий туннельный микроскоп (СТМ) принадлежит к семейству зондовых микроскопов и входит в состав инструментария большинства лабораторий, занимающихся проблемами нанометрологии и нанотехнологии. С помощью СТМ в сверхвысоком вакууме получают изображения отдельных атомов на чистой поверхности металлических и полупроводниковых образцов. Если вакуум не сверхвысокий (10–10 Торр), но высокий (10–5 Торр), то на поверхности наблюдают монослои адсорбированной воды в смеси с наночастицами (НЧ) органического происхождения размерами от 1 до 100 нм. Если исследование проводится в обычных лабораторных условиях, то к этим монослоям добавляются капиллярные нанослои воды толщиной в сотни нм [1].
Характерная электропроводность органических НЧ в адсорбированных нанослоях находится в диапазоне от металлической до диэлектрической в зависимости от состояния углерода, входящего в их состав. Если углерод внутри НЧ находится в состояниях, характерных для типичных углеводородов, то значения проводимости лежат в диапазоне от полупроводниковой до диэлектрической. Если углерод находится в виде компактных фуллереноподобных скоплений размером порядка 10 нм, то максимальные значения проводимости соответствуют металлам, а минимальные - узкозонным полупроводникам с шириной запрещенной зоны порядка 0,1 эВ.
Эти углеводородные НЧ участвуют в сложном конвективно-дрейфово-диффузионном движении вдоль исследуемой поверхности и активно вмешиваются во все зондовые процессы измерения. Такое вмешательство особенно заметно, когда между исследуемой поверхностью и зондом прикладывается электрическое напряжение более 1 В [2]. Электрическое поле сильно неоднородно на расстояниях от острия зонда порядка радиуса его кривизны 10 нм. Неоднородное поле поляризует НЧ и создает диэлектрофоретическую силу, пропорциональную градиенту квадрата напряженности электрического поля [3]. Эта сила втягивает НЧ в область сильного поля, т.е. способствует их накоплению под зондом именно в той области поверхности образца, которая анализируется с помощью зондового микроскопа. Для нанометрологии такие движения НЧ являются источником крупномасштабных методических погрешностей существенно негауссовского типа. С другой стороны, в нанотехнологии процесс диэлектрофореза используется для самосборки НЧ и рассматривается как перспективный способ создания макетов планарных наноэлектронных приборов типа полевых транзисторов c характерными размерами активной области около 10 нм, а также многофункциональных наноэлектронных устройств вроде «лаборатории на кристалле» [4].
Особенно перспективны для нанотехнологии такие процессы самоорганизации НЧ, когда в ответ на граничное или начальное возмущение в наносистеме разворачивается построение «снизу вверх» сложной наноструктуры. Эта наноструктура может состоять из миллионов упорядоченных НЧ и выполнять заранее заданную приборную функцию во многом аналогично тому, как действует органелла в живой биологической клетке.
Таким образом, исследование поляризации наночастиц в неоднородном электрическом поле зонда СТМ актуально как для зондовой нанометрологии, так и для зондовой нанотехнологии.
В данной работе для моделирования электрического поля вокруг металлических НЧ между зондом СТМ и подложкой использован метод граничных элементов [5]. Чтобы ускорить расчет для большого числа элементов, применен метод функций Грина [6-8]. При этом существенно изменен вид распределения вспомогательных зарядов вне анализируемого объема. Далее эти изменения подробно рассмотрены.
Расчет электростатического поля вокруг зонда и наночастиц. Формула Грина (1) выражает потенциал ![]() в точке
в точке ![]() снаружи объема, ограниченного поверхностью
снаружи объема, ограниченного поверхностью ![]() , через значения на этой поверхности самого потенциала
, через значения на этой поверхности самого потенциала ![]() и его нормальной производной
и его нормальной производной ![]() . Предполагается, что объемная плотность заряда во всех точках
. Предполагается, что объемная плотность заряда во всех точках ![]() отсутствует.
отсутствует.
![]() (1)
(1)
Здесь ![]() – известное (2) фундаментальное решение уравнения Лапласа, зависящее только от расстояния
– известное (2) фундаментальное решение уравнения Лапласа, зависящее только от расстояния ![]() между точками
между точками ![]() и
и ![]() , а
, а ![]() – его нормальная производная в точке
– его нормальная производная в точке ![]() на поверхности
на поверхности ![]() , также известная функция точек
, также известная функция точек ![]() и
и ![]() .
.

где ![]() (2)
(2)

Здесь ![]() – вектор нормали к поверхности в точке
– вектор нормали к поверхности в точке ![]() . В нашем случае наночастиц между зондом и подложкой поверхность
. В нашем случае наночастиц между зондом и подложкой поверхность ![]() состоит из отдельных поверхностей зонда
состоит из отдельных поверхностей зонда ![]() , подложки
, подложки ![]() и каждой из наночастиц
и каждой из наночастиц ![]() . Предполагаем, что наночастицы идеально проводящие и контактируют с поверхностью проводящей подложки. Поэтому все поверхности S- эквипотенциальные. Потенциалы
. Предполагаем, что наночастицы идеально проводящие и контактируют с поверхностью проводящей подложки. Поэтому все поверхности S- эквипотенциальные. Потенциалы ![]() на них известны и задаются внешним источником напряжения между зондом и подложкой (рис.1).
на них известны и задаются внешним источником напряжения между зондом и подложкой (рис.1).
Неизвестной величиной в правой части (1) является ![]() - нормальная производная потенциала. Т.е. неизвестна напряженность электрического поля на поверхностях зонда, подложки и НЧ, пропорциональная поверхностной плотности заряда. Чтобы ее найти, можно применить (3) - вариант формулы Грина (1), справедливый, когда точка
- нормальная производная потенциала. Т.е. неизвестна напряженность электрического поля на поверхностях зонда, подложки и НЧ, пропорциональная поверхностной плотности заряда. Чтобы ее найти, можно применить (3) - вариант формулы Грина (1), справедливый, когда точка ![]() лежит на поверхности
лежит на поверхности ![]() .
.
![]() (3)
(3)
Поскольку в этой формуле все значения потенциалов ![]() известны, ее рассматриваем как интегральное уравнение (4) относительно неизвестной напряженности
известны, ее рассматриваем как интегральное уравнение (4) относительно неизвестной напряженности ![]() на поверхности
на поверхности ![]() .
.
![]() (4)
(4)
Это интегральное уравнение становится матричным (5) после разбиения поверхности ![]() на отдельные элементы
на отдельные элементы ![]() . Предполагаем, что в пределах каждого k-го элемента поверхности искомая напряженность
. Предполагаем, что в пределах каждого k-го элемента поверхности искомая напряженность ![]() постоянна и принимает значение Fk.
постоянна и принимает значение Fk.
![]() m= 1…N (5)
m= 1…N (5)
Здесь N - число всех элементов на поверхностях зонда, подложки и наночастиц, а матричные элементы ![]() есть функция
есть функция ![]() , проинтегрированная по k-му элементу поверхности
, проинтегрированная по k-му элементу поверхности ![]() . Аналогично выглядят и элементы вектора
. Аналогично выглядят и элементы вектора ![]() .
.
![]() m = 1…N (6)
m = 1…N (6)

Для числа N всех элементов поверхности больше примерно 100 решение системы (5) N линейных уравнений занимает неприемлемо большое время. Чтобы сократить число этих уравнений, оставим в уравнении (4) неизвестной напряженность ![]() только на поверхностях НЧ. Чтобы убрать из (4) неизвестную напряженность
только на поверхностях НЧ. Чтобы убрать из (4) неизвестную напряженность ![]() на поверхностях зонда и подложки, применим метод функций Грина.
на поверхностях зонда и подложки, применим метод функций Грина.
Функция Грина для зонда и подложки. По методу функций Грина мы заменяем в формуле (1) фундаментальное решение ![]() такой функцией
такой функцией ![]() , которая не только имеет свойство «фундаментальности» функции
, которая не только имеет свойство «фундаментальности» функции ![]() , но и обращается в ноль в точках
, но и обращается в ноль в точках ![]() на поверхностях зонда
на поверхностях зонда ![]() и подложки
и подложки ![]() . Тогда неизвестная напряженность
. Тогда неизвестная напряженность ![]() в правой части (1) останется только в интеграле по поверхностям наночастиц
в правой части (1) останется только в интеграле по поверхностям наночастиц ![]() (7).
(7).
![]() (7)
(7)
Здесь ![]() –нормальная производная функции Грина
–нормальная производная функции Грина ![]() в точке
в точке ![]() на поверхности
на поверхности ![]() . Она станет известной функцией после нахождения функции Грина
. Она станет известной функцией после нахождения функции Грина ![]() . Таким образом, число уравнений в системе (5) уменьшится до числа элементов Nn, располагающихся только на поверхностях наночастиц
. Таким образом, число уравнений в системе (5) уменьшится до числа элементов Nn, располагающихся только на поверхностях наночастиц ![]() ., но не на поверхностях зонда и подложки.
., но не на поверхностях зонда и подложки.
Для нахождения функции Грина в аналогичной ситуации в работе [6] применялось вспомогательное распределение точечных и линейных зарядов вдоль оси зонда. Такое распределение достаточно для расчета силы притяжения зонда к поверхности, но недостаточно для расчета поля между зондом и произвольно расположенными наночастицами. Для расчета поля внутри экранированного объема в работе [7] применялось вспомогательное распределение точечных зарядов снаружи от объема. Действуя в этом же духе, мы рассмотрим вспомогательное распределение точечных зарядов внутри зонда.
Чтобы выяснить, каким требованиям должно удовлетворять искомое вспомогательное распределение зарядов, вернемся к уравнению (1). При его выводе (см. напр. [9, с. 123]) на функции ![]() и
и ![]() накладывались условия гармоничности и фундаментальности соответственно (8)
накладывались условия гармоничности и фундаментальности соответственно (8)
![]() (8)
(8)
![]()
Здесь ![]() - лапласиан, действующий на переменную
- лапласиан, действующий на переменную ![]() ,
, ![]() – дельта-функция Дирака,
– дельта-функция Дирака, ![]() - бесконечно удаленная поверхность.
- бесконечно удаленная поверхность.
Формула (1) получается после подстановки функций ![]() и
и ![]() в формулу Грина (9) вместо функций
в формулу Грина (9) вместо функций ![]() и
и ![]() соответственно.
соответственно.
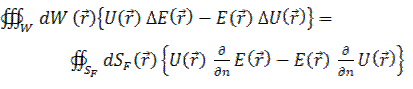 (9)
(9)
Здесь ![]() – элемент объема
– элемент объема ![]() около точки
около точки ![]() , а
, а ![]() – элемент полной поверхности
– элемент полной поверхности ![]() , окружающей весь объем
, окружающей весь объем ![]() . Эта поверхность состоит из бесконечно удаленной поверхности
. Эта поверхность состоит из бесконечно удаленной поверхности ![]() , а также поверхностей зонда
, а также поверхностей зонда ![]() , подложки
, подложки ![]() и наночастиц
и наночастиц ![]() . После применения условий гармоничности и фундаментальности (8) в левой части (9) остается только потенциал
. После применения условий гармоничности и фундаментальности (8) в левой части (9) остается только потенциал ![]() , а справа – правая часть формулы (1), причем из поверхности интегрирования
, а справа – правая часть формулы (1), причем из поверхности интегрирования ![]() исчезает поверхность
исчезает поверхность ![]() и остаются только поверхности зонда
и остаются только поверхности зонда ![]() , подложки
, подложки ![]() и наночастиц
и наночастиц ![]() .
.
Функция ![]() есть потенциал в точке
есть потенциал в точке ![]() , создаваемый точечным зарядом величиной -1/
, создаваемый точечным зарядом величиной -1/![]() , расположенным в той точке
, расположенным в той точке ![]() ., где мы вычисляем значение потенциала
., где мы вычисляем значение потенциала ![]() по формуле (1). Добавим к этому точечному заряду любую совокупность точечных зарядов {Qn}, расположенных вне объема интегрирования формулы (9) в точках
по формуле (1). Добавим к этому точечному заряду любую совокупность точечных зарядов {Qn}, расположенных вне объема интегрирования формулы (9) в точках ![]() . Тогда формула (1) по-прежнему будет верна. Но в ее правой части фундаментальное решение
. Тогда формула (1) по-прежнему будет верна. Но в ее правой части фундаментальное решение ![]() заменяется суммой фундаментальных решений
заменяется суммой фундаментальных решений ![]() , соответствующих точечному заряду в точке
, соответствующих точечному заряду в точке ![]() , и всем дополнительным зарядам Qn в точках
, и всем дополнительным зарядам Qn в точках ![]() внутри зонда. Таким образом, вместо (1) получаем (10).
внутри зонда. Таким образом, вместо (1) получаем (10).
![]() (10)
(10)
Здесь функция Грина ![]() и ее нормальная производная
и ее нормальная производная ![]() зависят от расположения
зависят от расположения ![]() и величины
и величины ![]() вспомогательных зарядов внутри зонда.
вспомогательных зарядов внутри зонда.
![]() (11)
(11)
![]()
Здесь M – полное число вспомогательных зарядов внутри зонда. Вид функций ![]() и
и ![]() приведен в (2). Величины, расположение и число вспомогательных зарядов можно выбирать произвольно, лишь бы функция
приведен в (2). Величины, расположение и число вспомогательных зарядов можно выбирать произвольно, лишь бы функция ![]() обращалась в ноль на поверхностях зонда
обращалась в ноль на поверхностях зонда ![]() и подложки
и подложки ![]() с заданной точностью.
с заданной точностью.
Поскольку поверхность подложки предполагается плоской, для обнуления ![]() на ее поверхности
на ее поверхности ![]() достаточно разместить под этой поверхностью зеркально расположенные заряды. К каждому точечному заряду над поверхностью подложки добавляем зеркальный заряд противоположного знака, расположенный под поверхностью. Получаем
достаточно разместить под этой поверхностью зеркально расположенные заряды. К каждому точечному заряду над поверхностью подложки добавляем зеркальный заряд противоположного знака, расположенный под поверхностью. Получаем
![]() (12)
(12)
Здесь звездочка означает зеркальное отражение в плоскости подложки. Начало отсчета координаты z выбрано на поверхности подложки, поэтому для любого ![]() получаем
получаем ![]() .
.
Таким образом, для расчета функции Грина остается обнулить выражение (12) для точек ![]() на поверхности
на поверхности ![]() зонда. Выбираем число этих поверхностных точек
зонда. Выбираем число этих поверхностных точек ![]() равным числу M вспомогательных зарядов и получаем систему M линейных уравнений для нахождения неизвестных величин
равным числу M вспомогательных зарядов и получаем систему M линейных уравнений для нахождения неизвестных величин ![]() вспомогательных зарядов внутри зонда при заранее заданном их расположении
вспомогательных зарядов внутри зонда при заранее заданном их расположении ![]() .
.
![]() m= 1…M (13)
m= 1…M (13)
Здесь ![]() и
и ![]()
Эта система линейных уравнений решается каждый раз, когда надо вычислить значение функции Грина или ее нормальной производной. Число вспомогательных зарядов много меньше числа граничных элементов. Поэтому решение такой системы экономит тем больше времени, чем мельче разбиение поверхностей НЧ. После нахождения ![]() и
и ![]() находим
находим ![]() из (5), а затем из (7) –потенциал
из (5), а затем из (7) –потенциал ![]() в любой требуемой точке
в любой требуемой точке ![]() .
.
Поляризация наночастиц. В качестве меры поляризации НЧ возьмем максимальное значение ![]() - нормальной составляющей напряженности электрического поля на поверхности этой НЧ. Она пропорциональна максимальной поверхностной плотности индуцированного заряда и фигурирует в выражении для максвелловского тензора напряжения, по которому находят силу, действующую на НЧ в произвольном неоднородном электростатическом поле.
- нормальной составляющей напряженности электрического поля на поверхности этой НЧ. Она пропорциональна максимальной поверхностной плотности индуцированного заряда и фигурирует в выражении для максвелловского тензора напряжения, по которому находят силу, действующую на НЧ в произвольном неоднородном электростатическом поле.
Чем меньше НЧ, тем сильнее броуновское движение и меньше диэлектрофоретическая сила. Поэтому важно исследовать зависимость максимального электрического поля на поверхности НЧ от ее размера. При диэлектрофоретическом образовании кучек, цепочек и т.д. из отдельных НЧ соседние частицы находятся не только во внешнем неоднородном поле, но и в неоднородном поле друг друга (взаимный диэлектрофорез). Поэтому важно знать, как поляризация зависит от взаимного расположения НЧ.
Для изучения зависимости распределения потенциала от параметров наночастиц были взяты такие же характерные параметры зонда, как в [6]. Угол раствора конуса – 30 град, радиус закругления нижней части – 10 нм. Высота всего зонда – более 100 нм. Потенциалы зонда и подложки относительно бесконечно удаленной точки равны 10 В и 0 В соответственно. Зазор между поверхностями зонда и подложки поддерживается равным 21 нм, так чтобы при максимальном сближении зонда и НЧ получался типичный туннельный зазор 1 нм при характерном радиусе НЧ 10 нм.
На рис. 1 показано разбиение поверхностей зонда и наночастиц на граничные треугольные элементы. Стрелками изображены векторы нормали к этим элементам (для ясности на рисунке оставлена только восьмая часть всех стрелочек). Они начинаются в тех точках, в которых вычисляются потенциалы и поля. Внутри каждого поверхностного элемента эти величины предполагаются постоянными. Поверхность зонда образована нижней и верхней сферическими поверхностями, гладко переходящими в боковую конусную поверхность.
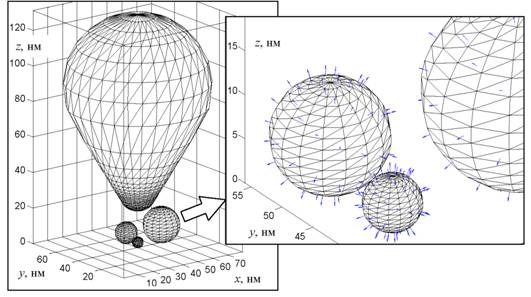
Рис. 1. Элементы поверхностей зонда и наночастиц
На рис. 2 приведены максимальные напряженности электрического поля Fmaxна поверхностях каждой из двух НЧ в зависимости от их взаимного расположения и размеров. На вставке показано расположение НЧ и зонда. При этом первая НЧ остается неподвижной прямо под зондом, а вторая НЧ постепенно удаляется от них по оси x на расстояние в несколько диаметров (указано стрелочкой на рис. 2), где происходит основное падение величины Fmax. Пока первая неподвижная НЧ в зазоре под зондом достаточно мала (радиус R1 меньше 6 нм) поляризация F2 второй подвижной НЧ с радиусом 10 нм падает при удалении от зонда примерно так же, как и в отсутствие первой НЧ в зазоре под зондом (пустые квадратики и треугольники на рис. 2). Но когда радиус R1 неподвижной НЧ в зазоре становится сравнимым с радиусом R2 подвижной НЧ (около 10 нм), поляризация F2 подвижной НЧ уменьшается (пустые кружки на рис. 2) примерно на 10 %. Большая неподвижная НЧ под зондом становится экраном для подвижной НЧ. Этот эффект экранирования проявляется и в постепенном увеличении поляризации F1 неподвижной НЧ по мере удаления от нее подвижной НЧ (черные квадратики и треугольники на рис. 2). Чем меньше радиус R1 неподвижной НЧ, тем больше относительный прирост δ ее поляризации F1 при удалении от нее подвижной НЧ. При уменьшении R1 с 10 нм до 1 нм значение δ возрастает примерно с 10 % до 50 %.
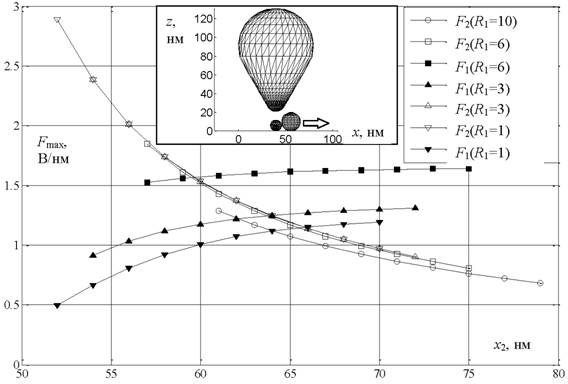
Рис. 2. Поляризация двух наночастиц
Добавление 3-й НЧ в направлении оси yпо соседству с 1-й НЧ под зондом примерно на 30 % уменьшает ее поляризацию, оставляя неизменным характер прироста δ ее поляризации F1 при удалении от нее подвижной НЧ (черные треугольники и ромбики на рис. 3). Это экранирование заметно и для подвижной НЧ, причем тем сильнее, чем больше различаются радиусы НЧ. Если 1-я НЧ мала (R1= 3 нм), то добавление 3-й НЧ с радиусом R3 =10 нм уменьшает поляризацию F2 подвижной НЧ примерно на 10 % (ромбики на рис. 2). С ростом 1-й НЧ до R1=10 нм F2 падает еще на 10 % (кружочки на рис. 2). Добавление НЧ рядом с подвижной НЧ вдали от зонда примерно так же ее экранирует (на 10 %), как и добавление НЧ вблизи зонда.
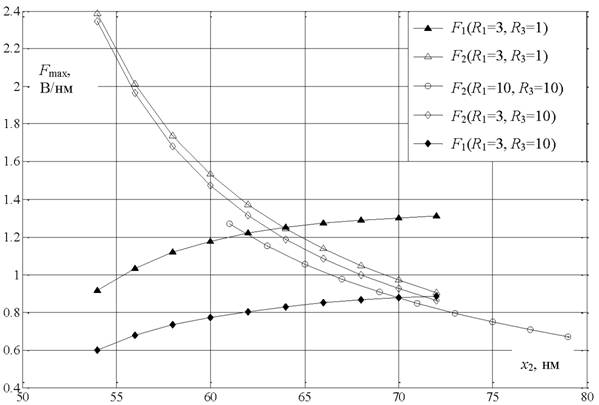
Рис. 3. Поляризация трех наночастиц
Выводы. Металлические наночастицы на проводящей поверхности под зондом туннельного микроскопа взаимно ослабляют поляризацию друг друга. Этот эффект экранирования тем сильнее, чем больше радиус экранирующей наночастицы и меньше радиус экранируемой наночастицы. Типичные значения ослабления поляризации составляют около 10 % при характерных радиусах 10 нм и напряженностях поля на поверхностях наночастиц в несколько единиц В/нм. По мере удаления наночастиц друг от друга взаимное экранирование затухает с характерным размером порядка 10 нм. Для расчета функции Грина зонда и подложки достаточно разместить около сотни вспомогательных точечных зарядов внутри зонда. Полученные результаты найдут применение в зондовых методах нанометрологии и при разработке диэлектрофоретических методов самоорганизации наночастиц в зондовой нанотехнологии.
Литература
1. Васильев С.Ю., Денисов А.В. Особенности туннельно-спектроскопических измерений в конфигурации воздушного сканирующего туннельного микроскопа //Журнал технической физики. 2000. Т. 70. N 1. С. 100 – 106.
2. Critical phenomena of water bridges in nanoasperity contacts /M.He, A.S.Blum, D.E.Aston et al //Journal of Chemical Physics. 2001. V. 114. N 3. P. 1355 – 1360.
3. Lynch B.P., Hilton A.M., Simpson G.J. Nanoscale Dielectrophoretic Spectroscopy of Individual Immobilized Mammalian Blood Cells //Biophysical Journal. 2006. V. 91. N 7. P. 2678 – 2686.
4. Electric field and tip geometry effects on dielectrophoretic growth of carbon nanotube nanofibrils on scanning probes /H. Wei, A.Craig, D.E.Aston et al //Nanotechnology. 2008. V. 19. 455303 (8 p.)
5. Ang W.T. A Beginner's Course in Boundary Element Methods //Universal Publishers. Boca Raton. USA. 2007. (253 p.). http://www.ntu.edu.sg/home/mwtang/bem2011.html
6. Sacha G. M., Sahagun E., Saenz J.J. A method for calculating capacitances and electrostatic forces in atomic force microscopy //Journal of Applied Physics. 2007. V. 101. 024310 (4 p.)
7. Practical Implementation of the Spatial Images Technique for the Analysis of Shielded Multilayered Printed Circuits/ J.S. Gomez-Diaz, M.Martinez-Mendoza, F.J.Perez-Soler et al //Microwave Theory and Techniques, IEEE Transactions on. 2008. V. 56. N 1. P. 131 – 141.
8. Konior J. Vertical and lateral electrostatic forces in a tip-plane system studied with a Green function plus surface charge method //Journal of Applied Physics. 2007. V. 101. 084907 (4 p.)
9. Методы расчета электростатических полей /Н.Н.Миролюбов, M.В.Костенко, М.Л.Левинштейн, Н.Н.Тиходеев //Высшая школа. Москва. 1963. 415 с.
Публикации с ключевыми словами: поляризация, сканирующий туннельный микроскоп, наночастица, электрический потенциал, уравнение Лапласа, функция Грина
Публикации со словами: поляризация, сканирующий туннельный микроскоп, наночастица, электрический потенциал, уравнение Лапласа, функция Грина
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



