научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 04, апрель 2012
УДК.534-141
МГТУ им. Н.Э. Баумана
ВВЕДЕНИЕ
Развитие ракетно-космической техники, создание космических аппаратов (КА) многократного запуска, совершающих различные манёвры на орбите, привели к усилению требований к системам отбора жидкости из баков КА.
В этой связи наиболее перспективными представляются капиллярные системы отбора жидкости (КСОЖ) из баков КА, отличающиеся высокой надежностью, эффективностью, долговечностью, стойкостью к воздействию агрессивных и криогенных компонентов, универсальностью применения, малой массой. Различные модификации таких систем находят в последнее время применения на новых типах КА и других летательных аппаратах.
Цель данной работы заключается в разработке приближенного аналитического метода для анализа краевой задачи об осесимметричных колебаниях двухслойной жидкости совместно с фазоразделяющей мембраной. При решении задачи использован метод собственных функций оператора Лапласа. Решение краевой задачи сводится к бесконечной системе алгебраических уравнений, при усечении которой получено частотное уравнение задачи, и, таким образом, задача сведена к проблеме собственных значений с применением метода Бубнова-Галёркина. частотных характеристик в зависимости от параметров бака.
Рассматриваемая задача является модельной, применительно к современным конструкциям ракетно-космической техники и ранее не рассматривалась.
Решение схожей задачи о колебаниях одной жидкости с диафрагмой было выполнено в работе [4], решение задачи о колебаниях жидкости со свободной поверхностью и упругим днищем - в работе [5]. В работе [6] рассмотрена задача о колебаниях стратифицированной жидкости с упругим днищем.
1. ПОСТАНОВКА ЗАДАЧИ

Рис. 1. Расчётная модель цилиндрического бака с КСОЖ
Полагаем бак жёстким, фазоразделитель будем рассматривать как непроницаемую мембрану, жестко закрепленную по своему контуру. Обозначим её прогиб через ![]() . Введём цилиндрическую систему координат, связанную с центром мембраны, как показано на рис. 1.
. Введём цилиндрическую систему координат, связанную с центром мембраны, как показано на рис. 1.
Примем плотности сред выше и ниже мембраны как ![]() и
и ![]() соответственно, разность плотностей обусловлена двухфазным состоянием криогенного компонента выше мембраны. Жидкость примем невязкой и несжимаемой.
соответственно, разность плотностей обусловлена двухфазным состоянием криогенного компонента выше мембраны. Жидкость примем невязкой и несжимаемой.
Рассматривая движение жидкости как безвихревое, введём потенциал скоростей жидкости, удовлетворяющий уравнению Лапласа, который для данной задачи примет следующий вид

где верхний индекс (1), (2) указывает на жидкость выше и ниже мембраны соответственно.
Условия непротекания в свою очередь примут вид

условие на свободной поверхности

Уравнение колебаний мембраны в осесимметричной постановке и динамическое граничное условие определяет выражение
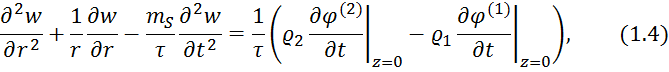
где ![]() масса мембраны,
масса мембраны, ![]() натяжение мембраны,
натяжение мембраны, ![]() разность давлений жидкости на мембрану.
разность давлений жидкости на мембрану.
Граничные условия для мембраны имеют вид
![]()
Кинематические условия при ![]() задают равенства
задают равенства

2. ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ
Введём обобщённые координаты ![]() и представим перемещения мембраны в виде разложения в ряд по собственным формам колебаний мембраны без жидкости
и представим перемещения мембраны в виде разложения в ряд по собственным формам колебаний мембраны без жидкости
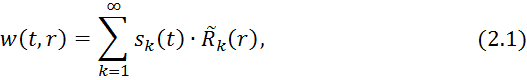
где ![]() формы собственных колебаний мембраны без жидкости, удовлетворяющие условиям полноты и ортогональности, а также граничным условиям при
формы собственных колебаний мембраны без жидкости, удовлетворяющие условиям полноты и ортогональности, а также граничным условиям при ![]() . Функции
. Функции ![]() должны удовлетворять уравнению собственных форм колебаний мембраны и в нашем случае имеют вид:
должны удовлетворять уравнению собственных форм колебаний мембраны и в нашем случае имеют вид:

где![]() корни функции Бесселя 1-го рода, нулевого порядка, причём
корни функции Бесселя 1-го рода, нулевого порядка, причём

![]() частота собственных осесимметричных колебаний
частота собственных осесимметричных колебаний ![]() -тона мембраны в отсутствии жидкости
-тона мембраны в отсутствии жидкости
Потенциал скоростей ![]() жидкости представим в виде
жидкости представим в виде

Решая методом Фурье уравнение Лапласа (1.1) для первой и второй жидкостей соответственно и удовлетворяя граничным условиям (1.2), а также - условию на свободной поверхности (1.3), очевидным образом получим выражения для потенциалов ![]() и
и ![]()

![]()

Вид функций ![]() определили из уравнения Лапласа, которое при разделении переменных в цилиндрических координатах имеет вид уравнения Бесселя
определили из уравнения Лапласа, которое при разделении переменных в цилиндрических координатах имеет вид уравнения Бесселя

решением которого имеет вид ![]() а с учётом граничных условий (1.2) и нормировки
а с учётом граничных условий (1.2) и нормировки ![]()
![]() .
.
Разложим![]() в ряд по ортогональным функциям
в ряд по ортогональным функциям

где 
Кинематическое условие на мембране (1.6) можем представить в виде

или, в развернутом виде

![]()
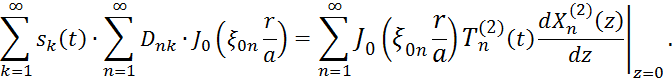
Помножив (2.5) на ![]() , проинтегрируем на интервале от 0 до
, проинтегрируем на интервале от 0 до ![]() и с учётом ортогональности функций Бесселя, получим выражения для потенциалов
и с учётом ортогональности функций Бесселя, получим выражения для потенциалов ![]()

![]()
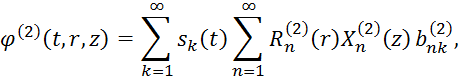
где

Запишем теперь динамическое граничное условие. Согласно (1.4) и (2.6) оно примет вид

![]()

Поскольку ![]() будем в дальнейшем опускать верхний индекс и писать
будем в дальнейшем опускать верхний индекс и писать ![]() .
.
Помножив полученное уравнение на ![]() и интегрировав в пределах от
и интегрировав в пределах от ![]() с учётом ортогональности функций, получим
с учётом ортогональности функций, получим

![]()

где

Запишем выражение (2.8) в виде

![]()
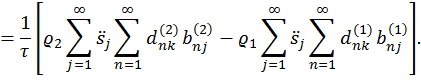
Обозначим

Тогда

![]()

Положим


Откуда получаем систему уравнений

Составив определитель k-го порядка которой, получаем характеристическое уравнение.

Важно отметить, что недиагональные члены определителя обратятся в ноль ввиду ортогональности функций Бесселя.
Зависимость частоты 1-го тона колебаний системы от радиального размера бака представлена на рис. 2. Данные взяты из работы [3], ![]() толщина мембраны,
толщина мембраны, ![]() плотность материала мембраны.
плотность материала мембраны.

Рис. 2. Зависимость частоты от радиуса бака ![]()
![]()
ЗАКЛЮЧЕНИЕ
В настоящей работе разработан приближенно-аналитический метод (на основе принципа Галёркина) рассматриваемой краевой задачи гидроупругости о свободных колебаниях двухслойной жидкости с упругим элементом в виде мембраны. Получено частотное уравнение этой краевой задачи. Найдены численные значения частот собственных колебаний и построена их зависимость от геометрических параметров бака.
ЛИТЕРАТУРА
1. Лойцянский Л.Г. «Механика жидкости и газа», М.: «Дрофа», 2003.- 840 c.
2. Мартинсон Л.К., Малов Ю.И. "Дифференциальные уравнения математической физики", М. Изд-во МГТУ им. Н.Э.Баумана, 2006.- 368 c.
3. «Капиллярные системы отбора жидкости из баков космических аппаратов» под ред. В.М.Поляева, М.: УНПЦ «Энергомаш», 1997.- 328 c.
4. Пожалостин А.А. "Свободные колебания жидкости в жестком круговом цилиндрическом сосуде с упругим плоским дном"//Известия высших учебных заведений. Cер. Авиационная техника.- 1963.- №4.
5. Петренко М.П. "Собственные колебания жидкости со свободной поверхностью и упругого днища цилиндрической полости"// Прикладная механика.- 1969.- Т. V, №6.- С. 44-50.
6. Андронов А.В. "Колебания идеальной стратифицированной жидкости в контейнере с упругим днищем"// Вопросы волновых движений жидкости : сб. науч. тр. - Краснодар: КубГУ,1987.
Публикации с ключевыми словами: уравнение Лапласа, капиллярные системы отбора жидкости, фазоразделитель, мембрана, потенциал скоростей жидкости, функции Бесселя, ортогональные функции
Публикации со словами: уравнение Лапласа, капиллярные системы отбора жидкости, фазоразделитель, мембрана, потенциал скоростей жидкости, функции Бесселя, ортогональные функции
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



