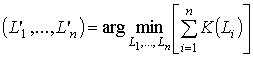научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 08, август 2011
МАДИ
Введение
Одной из задач руководства является построение рациональной организационной структуры, то есть структуры управления предприятием, наиболее полно соответствующей его назначению и приводящей к максимальной эффективности ее функционирования.
Задачи управления организационной структурой на настоящий момент являются малоизученными. Это связано, в первую очередь, со сложностью самой задачи, поскольку на принципы построения организационной структуры оказывает влияние весьма большое число факторов – размер организации, специфика технологии ее функционирования, структура ее документооборота, ограничения по возможностям передачи и переработки информации в системе управления, законодательные ограничения и другие. Вторая сложность связана с тем, что задача построения организационной структуры является «задачей верхнего уровня» по отношению к другим задачам управления. Для того, чтобы оценить эффективность того или иного состава сотрудников, вообще говоря, необходимо решить задачу синтеза оптимальных механизмов управления с учетом заданного состава, в частности, рассчитать оптимальную систему стимулирования для данного состава сотрудников.
Деловая игра наряду с другими методами обучения служит накоплению управленческого опыта формирования организационной структуры, близкого к реальному. Причем с помощью деловых игр это удается сделать несколько лучше, чем при других методах познания. Игра, во-первых, достаточно реально имитирует существующую действительность; во-вторых, создает динамичные организационные модели; в-третьих, более интенсивно побуждает к решению намеченных целей.
Другим назначением деловых игр является научное исследование. Если в основе игры лежит имитация производственных ситуаций, то при их адекватности реальным условиям метод становится удобным научным инструментом.
Педагогические принципы организации деловых игр
Для организации и проведения компьютерных деловых игр необходимо:
· подготовить руководство игры и группы обеспечения;
· подготовить методическое и техническое обеспечение;
· провести адаптацию деловой игры к соответствующему контингенту участников и условиям ее проведения;
· подготовить будущих участников игры, оценить уровень их готовности к игре;
· выполнить необходимые расчеты для оценки последствий различных вариантов решений, сформировать оптимальное или рациональное решение для каждого фрагмента игры.
Рассмотрим имитационные методы активного обучения и их основные характерологические признаки.
А. Метод анализа конкретных ситуаций, заключается в том, что обучаемым предъявляется ситуация, связанная с некоторым моментом функционирования конкретной системы. Задача обучаемых – коллективное принятие управленческого решения в конкретной ситуации. Характерологическим признаком анализа конкретной ситуации являются:
· наличие модели реальной системы, состояние которой рассматривается в некоторый дискретный момент времени;
· коллективная выработка решений;
· многоальтернативность решений;
· единая цель группы при выработке решений;
· наличие системы группового оценивания деятельности обучаемых.
· наличие управляемого эмоционального напряжения обучаемых.
Применение метода анализа конкретных ситуаций целесообразно в тех случаях, когда рассматривается отдельная, относительно сложная организационная, экономическая или управленческая задача, единственно правильное решение или правильное решение которой заранее известно преподавателю. За ним остается последнее слово при подведении итогов.
Б. Ролевые игры. В таких играх обычно отрабатывается умение руководить людьми. Для проведения игры необходимо моделировать управляющие системы, входящие в структуру конкретных систем. Среди участников игры при разборе предлагаемых ситуаций распределяются роли, которые могут носить групповой характер. Задача игры: выработка для исполнителя каждой роли на каждом этапе игры оптимальной стратегии поведения.
В отличие от анализа конкретных ситуаций в ролевых играх:
· необходимо наличие модели управляющей системы;
· решение принятое обучаемым воздействует только на управляющую систему, а не на объект управления;
· комплекс-модель управляющей системы носит динамический характер, где есть ролевое общение, в котором общение может зависеть от хода общения между партнерами.
В. Имитационные игры – это игры с разной целевой направленностью, для которых не свойственны некоторые из перечисленных характерологических признаков ролевых игр.
· В такой игре может быть только одна роль, которая тиражируется (создается множество экземпляров) каждым участником, который в свою очередь готовит свое решение.
· Отсутствует модель управленческой системы и объект управления, остается только модель среды, в которой необходимо принять решение. Здесь моделируется деятельность конкретных руководящих работников или специалистов.
· Отсутствие конфликтной ситуации.
Г. Организационно-деятельностные игры (ОДИ). К классу этих игр можно отнести: проблемные ролевые игры, проблемно-ориентированные деловые игры, апробационно-поисковые игры, инновационные игры. ОДИ применяют при решении сложных социально-производственных задач, когда требуется объединение усилий специалистов разных направлений. Игра базируется на основе предъявляемой игрокам исходной информации о состоянии реальной системы. Далее идет выработка, обсуждение и принятие решений по управлению указанной системой. В таких играх чаще решаются вопросы не оперативного управления, а о разработке программы управления. В игре выявляется комплекс проблем по управлению социально-экономической системой и пути решения этих проблем. В ОДИ обычно рассматриваются кризисные для системы состояния, обеспечивающие повышенную мотивацию участников игры и выработку решений, выводящих систему из кризиса.
Задача формирования организационной структуры
Для того чтобы эффективно решать задачу формирования организационной структуры, рассматривая большое число возможных вариантов структуры, эту задачу приходится несколько искусственно «отделять» от других задач управления и искать рациональную структуру с некоторым «типичным» составом и «стандартными» механизмами управления. И даже при этих упрощениях задачи построения организационной структуры остаются настолько сложными, что какие-либо общие методы их решения в настоящий момент отсутствуют.
Структура технологических потоков в существенной степени определяет организационную структуру, поэтому интересным представляется построение модели структуры управления технологическими связями организации. Технологический граф над множеством вершин N представляет ориентированный граф без петель T=<N, ET>, ребрам которого ![]() сопоставлены r-мерные вектора lT(u, v) с неотрицательными компонентами: lT:ET→Rr+. Вершины данного графа – это элементарные операции технологического процесса предприятия или конечные исполнители (рабочие места). Связь
сопоставлены r-мерные вектора lT(u, v) с неотрицательными компонентами: lT:ET→Rr+. Вершины данного графа – это элементарные операции технологического процесса предприятия или конечные исполнители (рабочие места). Связь ![]() в технологическом графе означает, что от элемента u к элементу v идет r-компонентный поток сырья, материалов, энергии, информации и т.п. Интенсивность каждой компоненты потока и определяется компонентами вектора lT(u, v).
в технологическом графе означает, что от элемента u к элементу v идет r-компонентный поток сырья, материалов, энергии, информации и т.п. Интенсивность каждой компоненты потока и определяется компонентами вектора lT(u, v).
В результате, основными задачами являются: подбор сотрудников под обязанности на основании тестового контроля и переподготовка сотрудников для соответствия требованиям. Причем деловые игры в данной постановке задачи наиболее адекватно подходят в качестве самой модели организационной структуры для принятия коалиционных решений. Функция выигрыша при этом может быть использована как шкала оценки уровня знаний.
Если «расположить» технологический граф в горизонтальной плоскости, то создание организации (или организационной структуры) можно сформулировать как задачу надстройки над технологическим графом дерева. Причем «верхними» узлами дерева будут менеджеры-контролеры, а «нижними» узлами, или листьями – вершины технологического графа.
Группа в узле v графа организации является объединением групп в узлах, непосредственно подчиненных узлу v:
| (1) |
Предполагается, что узел v графа организации контролирует технологические потоки только между вершинами подчиненной ему группы g(v). Определим вектор lT(g) суммарного потока между вершинами произвольной группы g как:
| (2) |
Поскольку общий поток внутри группы g(v) узла v равен lT(g(v)), а потоки lT(g(v1)),..., lT(g(vk)) уже контролируются непосредственными подчиненными узла v, то узел v должен непосредственно контролировать лишь поток LT(v)=lT(g(v))-lT(g(v1))-…-lT(g(vk)), где g(v1),…, g(vk) – группы в узлах-подчиненных {v1,..., vk}=Q(v).
Идентификация уровня квалификации
Для реализации процедур идентификации уровня подготовки в ходе проведения деловых игр предлагается итерационная процедура. При этом определение квалификационного уровня определенного сотрудника является отдельной задачей и ее решение может быть сведено к обработке экспертных оценок всех остальных сотрудников.
Пусть имеется N участников деловой игры, в процессе которой либо вручную, либо автоматически (анализ действий в соответствии со сценарием) каждый дает свою оценку “квалификационного уровня” другому, что может быть сведено в матрицу X, где xij – оценка i-ым участником “квалификации” j-го участника. Интересен вопрос согласованности этих оценок. При полном согласовании все строки должны совпадать.
Однако в общем случае строки не совпадают за счет субъективного мнения каждого. Наиболее естественным путем получения результирующей оценки является взвешенная оценка всех участников:
Xi = α1×x1i + α2×x2i + ... + αN×xNi, | (3) |
где αi – истинная оценка участника деловой игры.
Однако истинной оценкой будем считать ту, которую получим после преобразования с учетом всех построенных оценок. В результате получаем итерационную процедуру:
| (4) |
В качестве начальных весов можем взять веса X(0), определенные некоторым одним случайно или неслучайно выбранным участником. После этого взвесим оценку каждого этими весами, получим новые веса каждого и т.д. Анализ сходимости процедуры основывается на принципе сжимающих отображений.
Оптимизация организационной структуры
В результате построения графа организации для каждой связи технологического графа должен быть назначен ответственный, контролирующий данную связь. Если технологический граф T связный, то для того, чтобы каждая его связь кем-то контролировалась, необходимо наличие в графе организации узла, группа в котором совпадает со всем множеством исполнителей N. Это и будет корневой узел дерева организации.
Содержание каждого из узлов графа организации связано с определенными затратами. Будем считать, что затраты на содержание узла v зависят от потока LT(v), который непосредственно контролирует данный узел, и описываются некоторой функцией K(LT(v))≥0.
Тогда стоимость P(G) всего графа организации G=<V, E> (где V – множество управляющих узлов графа организации (то есть вершин, имеющих подчиненных), а E – множество дуг, определяющих взаимную подчиненность узлов) равна сумме стоимостей его узлов:
Таким образом, задачу определения структуры оптимальной системы управления технологическими связями можно сформулировать как задачу поиска оптимального дерева организации одной группы N на множестве исполнителей N с функционалом стоимости узла, заданным формулой (5).
Пусть построен некоторый граф организации G: определены узлы v1,…, vn, управляющие группами g1,…, gn и контролирующие потоки L1,…, Ln. Стоимость такой организации равна:
| (6) |
Обозначим ![]() сумму всех потоков технологического графа T. Для произвольной организации G выполнено равенство
сумму всех потоков технологического графа T. Для произвольной организации G выполнено равенство 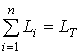 .
.
Временно допустим, что после построения графа организации можно произвольно перераспределять потоки между его узлами для уменьшения загруженности одних узлов и увеличения загруженности других. Тогда при заданном наборе узлов v1,…, vn для определения их загруженности L'1,…, L'n, приводящей к минимальной стоимости системы управления, необходимо решить задачу:
| (7) |
с учетом условия 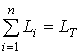 .
.
В силу зависимости функции K(·) от линейной комбинации компонент, можно r-компонентные потоки lT(u, v)=(lT(u, v)1,…, lT(u, v)r) заменить на однокомпонентные потоки ![]() .
.
В результате получаем задачу с однокомпонентными потоками и выпуклой функцией затрат K'(·). Решением данной задачи является равное распределение нагрузки между узлами графа организации – нагрузка L'1=…=L'n=LT/n.
Стоимость организации при такой загруженности узлов равна n·K'(LT/n), и это минимальная стоимость организации суммарного потока LT с n управляющими узлами.
Однако произвольное перераспределение загруженности между управляющими узлами невозможно, поскольку оно полностью определяется группами, которые контролируют узлы, и группами, которые контролируют их непосредственные подчиненные. Следовательно, мы можем только изменить граф организации, передав часть подчиненных одного узла другому. Вместе с передачей подчиненных произойдет и перераспределение потоков.
Однако на практике обычно достаточно найти «хорошую» организацию, затраты на содержание которой не сильно превышают минимальные. Для решения же этой задачи предлагается следующий алгоритм.
1. Найдем примерное количество узлов в дереве организации:
| (8) |
Если бы было возможно распределение потоков поровну между n узлами графа организации, то при количестве узлов в графе, равном n* достигался бы минимум затрат на содержание организации.
2. Определим «эталонный» поток L:=LT/n*, приходящийся на один узел.
3. Будем последовательно добавлять в граф организации узлы таким образом, чтобы контролируемый ими поток был как можно ближе к эталонному потоку L до тех пор, пора каждая связь технологического графа не будет контролироваться одним из узлов графа организации.
Таким образом, одним из обобщений рассматриваемой модели является допущение возможности нахождения в одном узле графа организации нескольких сотрудников.
Организация деловой игры
Оценки соответствия персонала должностным обязанностям в рамках формируемой организационной структуры естественным образом параметризуют организационную структуру. Важную роль в данном случае играют методы адаптивного тестового контроля и активного обучения в рамках проведения компьютерных деловых игр.
Самой простой игрой является та, в которых участники выбирают свои действия одновременно (игра Г0 в нормальной форме). При переходе к иерархическим играм последовательность ходов фиксирована – первым делает ход центр, а затем – участник. Можно усложнять модель и дальше, переходя к всё более сложным играм. Проведем логику перехода от более простых к более сложным задачам (рис. 1.), чтобы более сложная задача могла быть декомпозирована на более простые.
Если имеется один субъект, принимающий решения (рис. 1.а), то он описывается с точки зрения гипотезы рационального поведения (ГРП) как стремящийся максимизировать свою целевую функцию. Далее можно усложнить модель и рассмотреть несколько субъектов на одном уровне (рис. 1.б), описав их взаимодействие игрой Г0 в нормальной форме. Если ввести иерархию, то для двух субъектов (рис. 1.в) их взаимодействие описывается игрой Гi , где ![]() .
.
Предположим, что имеется структура «один начальник – несколько подчиненных» (рис. 1.г). Взаимодействие участников, находящихся на одном уровне, можно описывать игрой Г0. Взаимодействие «начальник-подчиненный» описывается игрой Гi . Тогда условно такую структуру можно представить игрой Гi, определенной на игре Г0, условно обозначив ее Гi(Г0). Далее, пусть есть несколько начальников (центров) и несколько подчиненных (рис. 1.д). На нижнем уровне участники играют игру Г0. Над ними центры играют иерархическую игру Гi, но центры, в свою очередь, разыгрывают на своем уровне игру Г0. В результате получим игру Г0(Гi(Г0)). Можно взять более сложную структуру с более сложным взаимодействием (рис. 1.е). Это будет иерархическая игра между уровнями, и "обычная" игра на каждом из уровней: (Г0(Гi(…Гi(Г0)…)).
Основная идея заключается в том, чтобы декомпозировать сложную структуру игры на набор более простых и воспользоваться результатами исследования последних. Кроме того, между играми и структурами существует глубокая связь – момент принятия субъектом решений определяет его "место" в организационной иерархии.
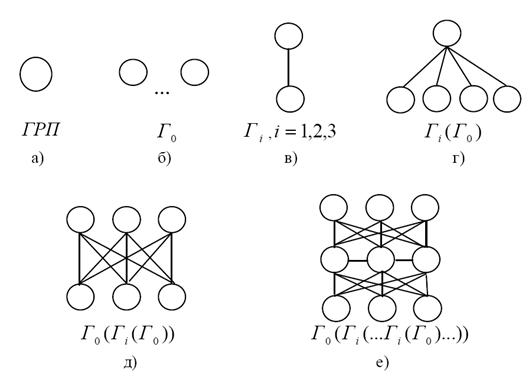
Рис. 1. Игры и структуры
Несомненно, полезно иметь такие механизмы формирования сценариев, когда несколько игр естественным образом объединяются для решения более крупной задачи, в том числе, и моделирования производственной ситуации.
Общий случай разработанной организационно-структурной среды многоролевой ДИ представлен на рис. 2., где:
G — многоролевая деловая игра (МРДИ);
Rj — роли, предусмотренные в G; 1 ≤ j ≤ NR, где NR — количество ролей, предусмотренных в G;
gi — созданные экземпляры G; 1 ≤ i ≤ Ng, где Ng — количество созданных экземпляров G;
rijk — экземпляры предусмотренных ролей в созданных экземплярах G; 1 ≤ j ≤ NR, 1 ≤ k ≤ NRj, где NRj — число созданных экземпляров роли Rj.
По своей структуре индивидуальная одноэкземплярная ДИ, имеющая возможность создания нескольких взаимодействующих экземпляров своей единственной роли, аналогична индивидуальной ДИ с единственным экземпляром этой роли, но поддерживающая несколько взаимодействующих экземпляров самой игры.
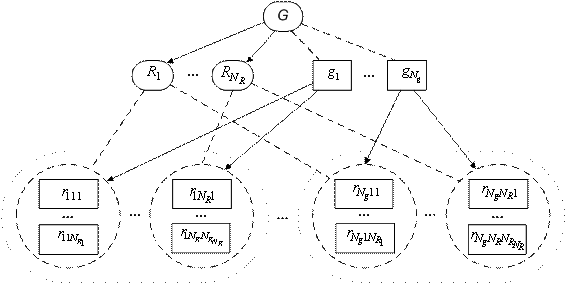
Рис. 2. Общий случай организационно-структурной среды многоролевой ДИ
Пунктирными линиями показаны отношения типа «класс-экземпляр». Стрелками показаны отношения принадлежности. При разработке тела ДИ в сценарии возможны различные варианты организации потоков управления (рис. 3.). Восьмиугольниками обозначены синхронизующие фрагменты.
а)  б)
б)  в)
в)  г)
г) 
Рис. 3. Варианты организации потоков управления в сценарии ДИ
Фрагменты рисунка соответственно определяют: а) ветвление; б) цикл; в) синхронизация всех экземпляров в пределах одной роли; г) синхронизация всех экземпляров всех ролей, входящих в синхронизирующий контур. На рис. 3.г пунктирной линией показан контур синхронизации, объединяющий фрагменты, относящиеся к разным ролям (нитям сценария). Синхронизироваться будут экземпляры только тех нитей, которые входят в контур.
Функционирование организационно-структурной среды ДИ определяется следующими параметрами, значения которых задаются при разработке игры: экземплярность ДИ (одно- или многоэкземплярная); ограничения на выбор ролей (могут ли тиражироваться и в каком количестве), может ли игрок для определенной роли быть заменен моделью.
Заключение
Таким образом, проведен системный анализ методов и моделей формирования организационной структуры управления промышленным предприятием. Показана необходимость решения задач оценки квалификационного соответствия реализации технологических операций. Проведен анализ и классификация деловых компьютерных игр в системе переподготовки персонала промышленных предприятий. Показана целесообразность использования организационно-деятельностных и многоролевых игр. Разработаны формализованные методы синтеза организационной структуры управления с точки зрения подбора персонала для каждой цепи технологического цикла общего производственного процесса предприятия. Разработаны методы, модели и алгоритмы формирования псевдооптимальной организационный структуры в плане стоимости реализации всех операций поддержания технологических процессов. Разработаны механизмы синхронизации действий пользователей в процессе многоролевой деловой игры и предложена методика оценки и переоценки квалификации персонала по результатам проведения деловой игры.
Список литературы
1. Баринов К.А., Остроух А.В., Рожин П.С., Учеваткин Д.А. Использование деловых игр при подготовке управленческих кадров автотранспортного предприятия // Инновационные технологии на транспорте и в промышленности: сб. науч. тр. / МАДИ (ГТУ). – М., 2007. – С. 30-37.
2. Баринов К.А., Остроух А.В., Суркова Н.Е. Реализация деловых игр в компьютерных системах обучения // Открытое и дистанционное образование, ╧ 3 (27), Томский государственный университет 2007. – С. 28-33.
3. Баринов К.А., Бугаев А.В., Буров Д.А., Остроух А.В. Опыт разработки и использования ролевых игр для подготовки и переподготовки специалистов предприятий промышленности и транспортного комплекса // Научный вестник МГТУ ГА, вып. ╧141 / МГТУ ГА. – М. 2009. – С. 189-197.
4. А.А. Воронин, С.П. Мишин. Алгоритмы поиска оптимальной структуры организационной системы // Автоматика и телемеханика. 2002. ╧5. – С. 120–132.
5. Овсиевич Б.Л. Модели формирования организационных структур. – Л.: Наука, 1979.
6. Цвиркун А.Д. Основы синтеза структуры сложных систем. – М.: Наука, 1982.
7. Форд Л., Фалкерсон Д. Потоки в сетях. – М.: Мир, 1966.
8. Бурков В.Н., Заложнев А.Ю., Новиков Д.А. Теория графов в управлении организационными системами. – М.: Синтег, 2001. – 124 с.
9. Пугачев В.П. Тесты, деловые игры, тренинги в управлении персоналом. – М., 2002.
10. Платов В.Я. Деловые игры: разработка, организация, проведение. – М., 1991.
11. Баранов П.В., Сазонов Б.В. Игровая форма развития коммуникации, мышления, деятельности. – М., 1989.
12. Гуреев А.Б., Динова Н.И., Кулжабаев Н.М., Щепкин А.В. Учебные автоматизированные деловые игры. – М.: ИПУ им. В.А. Трапезникова РАН, 1999.
13. Галлямов Ф.Ф. Деловые игры – эффективный инструмент активного обучения. – Владивосток, 1995.
Публикации с ключевыми словами: обучение, управление, организационная структура предприятия, деловая игра, технологический граф, иерархическая игра, сценарий, организационно-структурная среда, каркас
Публикации со словами: обучение, управление, организационная структура предприятия, деловая игра, технологический граф, иерархическая игра, сценарий, организационно-структурная среда, каркас
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||
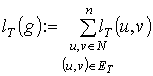 .
.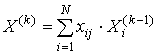
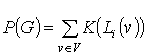
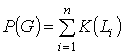 .
.