научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 09, сентябрь 2011
Введение
Стратегия развития любого промышленного предприятия или коммерческой фирмы направлена, прежде всего, на получение прибыли. Прибылью можно пожертвовать ради проникновения на рынок, ради внедрения на рынок новой продукции, ради увеличения доли присутствия, но нельзя игнорировать вовсе. Общеизвестно, что прибыль возникает за счет продажи продукции по цене, превышающей издержки, поэтому получать ее можно либо устанавливая соответствующую цену, либо сокращая издержки. Причем диалектика конкурентной борьбы заставляет предпринимателей постоянно разрываться между стремлением получить монопольные позиции, гарантирующие получение прибыли, хотя бы в небольшом сегменте рынка, и поиском более прибыльных сфер деятельности, приводящим к подрыву чьих-то других монопольных позиций на рынке.
Анализ
Распространение продукции – одна из «трудоемких» и дорогостоящих задач маркетинга. Она предполагает выбор каналов распределения, решения относительно объемов и темпов охвата рынка, расположения продукции на рынке, формирования и поддержания определенных запасов, транспортировки и др. Эти вопросы представляют маркетинговую логистику. Они требуют от предприятия постоянного и неослабного внимания и составляют львиную долю текущих задач управления производством и реализацией. В комплексе маркетинга распространение, также как и ценообразование является одним из рычагов завоевания или удержания целевого сегмента рынка.
Продажа продукции длительного пользования или сложной техники предполагает оказание покупателям услуг по монтажу и сервисному обслуживанию. Здесь требуется не только квалифицированный и обученный персонал и соответствующее оборудование, но и содержание складских помещений, ведение разнообразных форм учета, планирование и осуществление закупок расходных материалов и запасных частей. На посредников также ложится функция ведения переговоров с заказчиками или организация своей сбытовой сети. В этом случае к издержкам и финансовым затратам прибавляется решение организационных и юридических вопросов.
Для описания коллективного поведения агентов недостаточно определить их предпочтения и правила индивидуального рационального выбора по отдельности. В случае, когда в системе имеется единственный агент, гипотеза его рационального (индивидуального) поведения предполагает, что агент ведет себя таким образом, чтобы выбором действия максимизировать значение своей целевой функции. В случае, когда агентов несколько, необходимо учитывать их взаимное влияние: в этом случае возникает игра – взаимодействие, в котором выигрыш каждого агента зависит как от его собственного действия, так и от действий других агентов. Если в силу гипотезы рационального поведения каждый из агентов стремится выбором действия максимизировать свою целевую функцию, то понятно, что в случае нескольких агентов индивидуально рациональное действие каждого из них зависит от действий других агентов.
Теоретико-игровые модели некооперативного взаимодействия
Проведем анализ теоретико-игровой модели некооперативного взаимодействия между n агентами, предполагая, что они принимают решения одновременно и независимо, не имея возможности договариваться о выбираемых действиях, перераспределять получаемую полезность (выигрыш) и т.д.
Каждый агент осуществляет выбор действия xi, принадлежащего допустимому множеству Xi, ![]() – множеству агентов. Выбор действий агентами осуществляется однократно, одновременно и независимо.
– множеству агентов. Выбор действий агентами осуществляется однократно, одновременно и независимо.
Выигрыш i-го агента зависит от его собственного действия ![]() от вектора действий
от вектора действий
| (1) |
оппонентов N\{i} и от состояния природы ![]() , и описывается действительнозначной функцией выигрыша
, и описывается действительнозначной функцией выигрыша ![]() где
где ![]() – вектор действий всех агентов. При фиксированном значении состояния природы совокупность
– вектор действий всех агентов. При фиксированном значении состояния природы совокупность ![]() множества агентов, множеств их допустимых действий и целевых функций представляет игру в нормальной форме. Решение игры в данной модели (равновесие) представляет множество устойчивых в том или ином смысле векторов действий агентов.
множества агентов, множеств их допустимых действий и целевых функций представляет игру в нормальной форме. Решение игры в данной модели (равновесие) представляет множество устойчивых в том или ином смысле векторов действий агентов.
Предполагается, что каждый агент будет стремиться выбрать наилучшие для него (с точки зрения значения его целевой функции) действия при заданной обстановке. Обстановкой для него будет совокупность состояния природы ![]() и обстановки игры
и обстановки игры ![]() . Принцип принятия им решения о выбираемом действии (при фиксированных обстановке и состоянии природы) в данной модели определяется следующим образом:
. Принцип принятия им решения о выбираемом действии (при фиксированных обстановке и состоянии природы) в данной модели определяется следующим образом:
| (2) |
Под решениями в данной постановке задачи понимаются объемы производства, цены на производимую продукцию, накладные расходы на маркетинговые исследования и др.
Анализ используемых методик показал, что существующие подходы к определению необходимого количества и номенклатуры поставляемых промышленных изделий были разработаны для плановой экономики и их использование в условиях рынка неэффективно. В некоторых работах вопросы определения потребности на основе маркетинговых исследований проработаны достаточно глубоко, однако в основном они носят общетеоретический характер, и малопригодны для практического использования. Регрессионные модели, применяемые в настоящее время, требуют частого пересмотра предикторов, что сопряжено с трудоемким процессом определения корреляционной значимости факторов в изменяющейся внешней среде.
В ряде работ рассматриваются задачи сбыта продукции центром и максимизация его прибыли за счет равновесного состояния предприятий-потребителей. В данной работе поставлена и решена обратная задача – задача выбора производителей для размещения производственных заказов, что приводит к конкуренции последних в рамках проведения конкурсных процедур (рис. 1.).

Рис. 1. Согласование цен и объемов производственных заказов
В настоящей работе проведен анализ задач управления реализацией продукции в условиях централизованной схемы и в условиях конкуренции. Первая задача связана с определением согласованных цен на заказы по производству и сбыту, которая рассматривается как оптимизационная, а затем – как игровая. В оптимизационной постановке предполагается, что цены, предлагаемые потребителями, заданы и не меняются. Задача центра (центром можно считать некоторый регион с его региональной стратегией производства и реализации промышленной продукции) в этом случае – определить оптимальную согласованную цену и, соответственно, множество производителей, которые будут участвовать в реализации производственного заказа. В игровой постановке потребители могут менять предлагаемые ими цены. Это и создает игровую ситуацию.
Формирование конкурсных механизмов получения заказов
Предполагается, что подбираются исполнители производственных заказов, каждый агент может претендовать на право реализации различных операций. Обозначим Aij – минимальную цену, по которой агент i еще берется за операцию j, Sij – цена за операцию, предлагаемая агентом i (очевидно, Sij³Aij). Центр (руководитель проекта) должен назначить все операции так, чтобы суммарная стоимость их реализации была минимальной. Примем, что каждый агент берется за реализацию не более, чем одной операции. Для формализации задачи принятия решений центром обозначим xij=1, если операция j назначается агенту i и xij=0 в противном случае. Тогда задачу распределения операций по агентам (сложный конкурс) можно представить в виде следующей математической задачи:
где n – число агентов, m – число операций. При этом стоимость j-ой операции равна  . Фактически здесь переплетаются несколько конкурсов (по числу операций), связанных между собой условием, что агент может быть победителем только в одном из них (то есть может выполнять в итоге только одну операцию). Анализ данного конкурсного механизма в существенной степени зависит от соотношения числа операций и числа агентов.
. Фактически здесь переплетаются несколько конкурсов (по числу операций), связанных между собой условием, что агент может быть победителем только в одном из них (то есть может выполнять в итоге только одну операцию). Анализ данного конкурсного механизма в существенной степени зависит от соотношения числа операций и числа агентов.
Ситуация равновесия Нэша соответствует назначению операций, минимизирующих сумму объективных затрат:
| (4) |
Действительно, пусть {S*ij} – ситуация равновесия. Пусть x*ij=1. Обозначим ∆i=Sij*–Aij. Если Sik–Aik>∆i, то агент будет уменьшать Sik, надеясь получить операцию k и обеспечить больший выигрыш. Это уменьшение будет продолжаться до Sik=Aik+∆i. Если же Sik<Aik+∆i, то увеличение Sik до величины Aik+∆i, очевидно, не изменит назначения операций.
Поэтому решение задачи (3) со значениями {S*ij} эквивалентно решению такой же задачи со значениями Sij=Aij+∆i, i,j=1..n. Наконец, естественно принять, что все агенты, не получившие операций, будут сообщать минимальные оценки Sij=Aij, надеясь получить какую-либо операцию. Отсюда следует, что назначение операций, минимизирующее  , минимизирует и
, минимизирует и  .
.
Рассмотрим случай, когда число агентов равно числу операций. Пусть S={Sij} – некоторая ситуация (совокупность цен, предлагаемых агентами), а xij(S) – соответствует решению задачи назначения. Если агент увеличит цены всех операций на одну и ту же величину S’ij=Sij+∆i, j=1..n, то решение задачи назначения не изменится, и агент получит ту же операцию, но по более высокой цене. Поэтому, естественно, возникает тенденция роста цен. Ограничим цену каждой операции некоторой величиной Lj (лимитная цена операции). Ясно, что хотя бы по одной операции каждый агент предложит лимитную цену.
Ситуация существенно меняется при появлении еще одного агента. При этом договорные цены в ситуации равновесия определяются уже не лимитными ценами {Lj}, а минимальными ценами {Aij}. Если принять, что лимитные цены достаточно велики, то можно показать, что они никак не влияют на равновесные цены.
Пусть агенты перенумерованы таким образом, что агент с номером i получает операцию i, а агент с номером (m+1) вообще не получает операции. В этом случае Ф0=ΣAij определяет оптимальное решение задачи минимизации ΣAij×xij .
В данной ситуации агент (m+1) сообщает в равновесии минимальные цены Sm+1,j=Am+1,j, а остальные агенты – цены Sij=Aij+Δi, i=1..m.
Для определения Δi решается m задач следующего вида:
| (5) |
при ограничениях:
| (6) |
Фактически проведена замена агента k на агента (m+1) в задаче назначения операций. Обозначим Фk значение целевой функции в оптимальном решении этой задачи. При этом Фk³Ф0 для всех k. Пусть теперь Δk>Фk–Ф0. В этом случае решение задачи минимизации Σ (Aij+Δi)xij не будет совпадать с решением задачи минимизации ΣAijxij. Поэтому в ситуации равновесия должно иметь место Δk£Фk–Ф0, а так как агенты заинтересованы в увеличении Δk, то в равновесии Δk=Фk–Ф0 и S*ij=Aij+Фi–Ф0, Фm+1=Ф0. Эффективность конкурсного механизма в случае n=m+1 определяется выражением:
| (7) |
Поскольку все Фi, i=1..n определяются на основе минимальных цен Aij, то эффективность конкурсного механизма определяется только минимальными ценами и не зависит от лимитных цен (при достаточно больших лимитных ценах).
Формализованное представление деловой игры в условиях конкуренции участников
Адекватным математическим инструментом моделирования связей между объектами являются графы. В рамках рассматриваемых моделей сетевого взаимодействия вершинами графа являются игроки, а дуга интерпретируется как наличие направленной связи между игроками.
Во многих сетевых играх для образования связи необходимо согласие обоих игроков – например, игрок по каким-либо причинам может отказаться принимать информацию от другого игрока. Итак, чтобы модель сетевой игры стала стратегической моделью, необходимо формализовать возможности игроков по образованию связей.
Желание i-го игрока образовать связь ij можно описать переменной xijout, которая равна единице, если игрок i хочет образовать связь ij, и нулю в противном случае. Индекс «out» при переменной показывает, что связь ij по отношению к игроку i является исходящей. Если xijout равна единице, будем говорить, что игрок i имеет предложение к игроку j.
Аналогично можно определить переменную xijin , говорящую о том, что игрок i согласен на образование дуги ji от игрока j. Индекс «in» говорит о том, что дуга ji является входящей по отношению к игроку i. Если xijin равно единице, будем говорить, что игрок i принимает предложение игрока j.
Действие xi игрока в сетевой игре представляет пару xi=(xjout, xiin) векторов xjout=(xj1out,…, xjnout), xjin=(xj1in,…, xjnin). Множество всевозможных пар этих векторов обозначим через Xi0 .
Таким образом, действие игрока определяет, по сути, множество его оппонентов, к которым игрок хочет образовать исходящую связь, и множество оппонентов, на образование входящей связи от которых игрок согласен.
Тогда в каждой конкретной игре множество Xi допустимых действий i-го игрока будет подмножеством множества Xi0.
Профиль действий игроков в сетевой игре представляет пару x=(xout, xin) квадратных матриц размера n, элементами которых являются компоненты допустимых xijout, xijin действий игроков. Множество профилей действий сетевой игры будет представлять декартово произведение ![]() .
.
Обстановка x-i для i-го игрока представляет пару x-i=(x-iout, x-iin) матриц размера n´(n-1), элементами которых являются компоненты допустимых действий xijout, xijin всех игроков, кроме i-го. Профиль действий x складывается из действия игрока xi и его обстановки x-i, в этом случае будем считать, что x=(xi, x-i).
Пусть реализовался некоторый профиль действий x=(xout, xin). Тогда, если мы считаем, что для образования связи ij необходимо и достаточно согласия обоих игроков, результирующая сеть g определяется поэлементным умножением матрицы xout на транспонированную матрицу xin, т.е. ![]() . Множество сетей, достижимых при заданном множестве профилей действий X, обозначим через G(X).
. Множество сетей, достижимых при заданном множестве профилей действий X, обозначим через G(X).
В результате стратегическую модель сетевой игры можно определить как совокупность ![]() множества игроков N, их функций выигрыша fi(×),
множества игроков N, их функций выигрыша fi(×), ![]() и множеств допустимых действий
и множеств допустимых действий ![]() .
.
Программные аспекты формирования сценария деловой игры
Следующая задача связана с формализацией представления сценария действий пользователей в ходе деловой игры. Между основной нитью сценария и вспомогательными процессами возможно взаимодействие пользовательских процессов, обмен данными и синхронизация. Фоновые процессы также могут взаимодействовать между собой (рис. 2.).

Рис. 2. Общая схема организации выполнения и взаимодействия фоновых пользовательских процессов
Для организации выполнения фонового процесса в сценарий вводятся дополнительные фрагменты 3-х типов:
· создающие (C) — создают фоновый процесс;
· уничтожающие (D) — принудительно уничтожают фоновый процесс (рис. 3.а);
· ожидающие (WE) — блокируют выполнение основной нити сценария в ожидании наступления некоторого события, связанного с выполнением фонового потока. Их частный случай (WT) — ожидание самостоятельного завершения фонового процесса. Для ожидающего фрагмента также может быть задано максимальное время ожидания. Тогда ожидающий фрагмент блокирует выполнение основной нити сценария до момента наступления заданного события, связанного с выполнением фонового процесса, либо до истечения максимального времени ожидания (рис. 3.б). Наступление события связано с изменением состояния некоторого ресурса, которым может быть сам фоновый процесс или любой другой объект.
· а)  б)
б)  в)
в) 
Рис. 3. Организация параллельных пользовательских процессов
а) с принудительным уничтожением фонового процесса
б) с ожиданием самостоятельного завершения фонового процесса
в) комбинированный вариант завершения
Эти дополнительные фрагменты также являются невизуальными (не имеют визуального представления). Фоновые процессы существуют не дольше времени проигрывания структурного элемента, в контексте которого он был порожден. При создании фонового процесса его идентификатор помещается во внутренний список фоновых процессов породившего его экземпляра проигрывателя. Этот список используется для принудительного уничтожения экземпляром проигрывателя фоновых процессов, которые на данный момент времени уже не должны существовать, но по каким-либо причинам не были уничтожены соответствующими фрагментами сценария структурного элемента.
Pk, Pm — фоновые процессы. Пунктирными стрелками с закрашенным наконечником показаны управляющие действия, связанные с созданием и уничтожением фоновых процессов. Пунктирными стрелками с наконечником в виде уголка показаны сообщения от фоновых процессов, сигнализирующие о наступлении ожидаемого события. Жирными стрелками показано взаимодействие между фрагментами основной нити сценария и фоновыми процессами, а также взаимодействие фоновых процессов между собой.
Фрагменты основной нити сценария могут взаимодействовать с фоновыми процессами посредством: общей памяти; именованных каналов; файлов; баз данных; других разделяемых объектов. Возможен комбинированный вариант завершения фонового процесса (рис. 3.в), при котором в течение заданного периода времени ожидается самостоятельное завершение фонового процесса. Если за указанный интервал времени процесс не завершился, то он завершается принудительно.
В виде фоновых процессов имеет смысл организовывать невизуальные процессы, выполняющие вспомогательные, обслуживающие функции для основной нити сценария. В основной нити сценария реализуются элементы пользовательского интерфейса, которые могут взаимодействовать с фоновым процессом. Использование параллельных процессов в пределах одного экземпляра проигрывателя способствует формированию более компактного сценария и его более эффективному в плане организации во времени выполнению.
Заключение
Проведен системный анализ принципов и методов распространения и продвижения продукции в условиях конкуренции, который показал необходимость выполнения работы по созданию программно-математических методов и инструментальных средств для использования многоролевых деловых игр при определении согласованной ценовой политики в условиях конкуренции. Проведен анализ игровых моделей выбора стратегий управления реализацией продукции, который определил необходимость постановки и решения задачи назначения конкурсной цены в случае равного и неравного количества агентов и операций. Предложены подходы к формализованному описанию действий пользователей в ходе многоролевой игры, что позволило разработать программные компоненты расширения функционала программно-инструментальной среды конструирования многоролевых деловых игр.
Список литературы
1. Баринов К.А., Остроух А.В., Рожин П.С., Учеваткин Д.А. Использование деловых игр при подготовке управленческих кадров автотранспортного предприятия // Инновационные технологии на транспорте и в промышленности: сб. науч. тр. / МАДИ (ГТУ). – М., 2007. – С. 30-37.
2. Баринов К.А., Бугаев А.В., Буров Д.А., Остроух А.В. Опыт разработки и использования ролевых игр для подготовки и переподготовки специалистов предприятий промышленности и транспортного комплекса // Научный вестник МГТУ ГА, вып. ╧141 / МГТУ ГА. – М. 2009. – С. 189-197.
3. Баринов К.А., Остроух А.В., Суркова Н.Е. Реализация деловых игр в компьютерных системах обучения // Открытое и дистанционное образование, ╧ 3 (27), Томский государственный университет 2007. – С. 28-33.
4. Пугачев В.П. Тесты, деловые игры, тренинги в управлении персоналом. – М., 2002.
5. Платов В.Я. Деловые игры: разработка, организация, проведение. – М., 1991.
6. Баранов П.В., Сазонов Б.В. Игровая форма развития коммуникации, мышления, деятельности. – М., 1989.
7. Гуреев А.Б., Динова Н.И., Кулжабаев Н.М., Щепкин А.В. Учебные автоматизированные деловые игры. – М.: ИПУ им. В.А. Трапезникова РАН, 1999.
8. Галлямов Ф.Ф. Деловые игры – эффективный инструмент активного обучения. – Владивосток, 1995.
9. Бурков В.Н., Кондратьев В.В. Механизмы функционирования организационных систем. – М.: Наука, 1981. – 384 с.
10. Гермейер Ю.Б. Игры с непротивоположными интересами. – М.: Наука, 1976. – 327 с.
11. Горелик В.А., Горелов М.А., Кононенко А.Ф. Анализ конфликтных ситуаций в системах управления. – М.: Радио и связь, 1991. – 288 с.
12. Горелик В.А., Кононенко А.Ф. Теоретико-игровые модели принятия решений в эколого-экономических системах. – М.: Радио и связь, 1982. – 144 с.
13. Губко М.В. Механизмы управления организационными системами с коалиционным взаимодействием участников. – М.: ИПУ РАН, 2003. – 118 с.
14. Губко М.В., Новиков Д.А. Теория игр в управлении организационными системами. – М.: Синтег, 2002. – 148 с.
15. Кононенко А.Ф., Халезов А.Д., Чумаков В.В. Принятие решений в условиях неопределенности. – М.: ВЦ АН СССР, 1991. – 211 с.
16. Кукушкин Н.С., Морозов В.В. Теория неантагонистических игр. – М.: МГУ, 1984.
17. Нейман Д., Моргенштерн О. Теория игр и экономическое поведение. – М.: Наука, 1970.
18. Новиков Д.А., Петраков С.Н. Курс теории активных систем. – М.: Синтег, 1999. – 108 с.
19. Новиков Д.А., Чхартишвили А.Г. Рефлексивные игры. – М.: Синтег, 2003. – 160 с.
20. Воробьев Н.Н. Основы теории игр. Бескоалиционные игры. – М.: Наука, 1984.
21. Воробьев Н.Н. Теория игр для экономистов-кибернетиков. – М.: Наука, 1985.
22. Оуэн Г. Теория игр. – М.: Мир, 1971.
23. Мулен Э. Кооперативное принятие решений: аксиомы и модели. – М.: Мир, 1991.
24. Бондарева О.Н. Некоторые применения методов линейного программирования к теории кооперативных игр // Проблемы кибернетики. Вып. 10. – М.: Физматгиз, 1963. – С. 119 – 140.
25. Нэш Д. Бескоалиционные игры / Матричные игры. – М.: Физматгиз, 1961. – С. 205 – 221.
26. Петросян Л.А., Зенкевич Н.А., Семина Е.А. Теория игр. – М.: Высшая школа, 1998.
Публикации с ключевыми словами: принятие решения, деловая игра, сценарий, многоролевая игра, конкуренция, конкурсный механизм, некооперативное взаимодействие, агент, гипотеза рационального поведения, фоновый процесс
Публикации со словами: принятие решения, деловая игра, сценарий, многоролевая игра, конкуренция, конкурсный механизм, некооперативное взаимодействие, агент, гипотеза рационального поведения, фоновый процесс
Смотри также:
- Формальные модели представления и организации деловых игр
- Формирование организационной структуры управления промышленным предприятием с использованием многоролевых деловых игр
- Один из подходов к оценке развития аномальной ситуации ходе полета пилотируемого космического аппарата для выбора рационального решения по её парированию
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||

 ,
,  ,
,  ,
,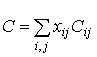 .
.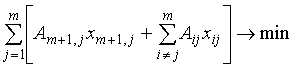 ,
,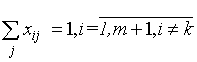 ,
,  .
. .
.


