научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2009
УДК 004
УДК 004.3 +519.6
МГТУ им. Н.Э. Баумана
Во второй части статьи рассмотрены операции стягивания ребер и подразбиения ребра ультра- и гиперграфа, удаления вершины из образов и прообразов заданного множества ребер, удаления ребра из образов и прообразов заданного множества вершин и формирования части графа.
Операции стягивания и подразбиения ребра необходимы, например, для снижения размера входа задачи при анализе планарности графа и изменения структуры объекта с целью улучшения характеристик его функционирования (увеличения пропускной способности, согласования параметров компонентов и соединений и т. п.).
Операции удаления вершин и ребер из образов и прообразов обеспечивают изменение логики функционирования объекта. Операция формирования части графа осуществляет выделение фрагмента структуры объекта для снижения размерности задач анализа при блочно-иерархическом проектировании.
Стягивание рёбер uf и uk ультраграфа HU или гиперграфа H – рис. 7. Соответствует проектной операции соединения двух цепей.

Рисунок 7 – Фрагмент схемы до и после соединения цепей с1 и с2 (а), ее модель в виде ультраграфа HU и результат HU1 стягивания рёбер u1 и u2 (б), гиперграф схемы H и
результат операции H1 (в)
Задаются имена стягиваемых рёбер uf, uk и заменяющего их ребра ut.
Обозначение операции: ╣(HU (X, U), uf, uk, ut) для ультраграфа и
╣(H (X, U), uf, uk, ut) для гиперграфа.
Условие корректности операции: uf, uk Î U.
В результате выполнения операции получаем ультра- или гиперграф
HU1 (X1, U1) = ╣(HU (X, U), uf, uk, ut) или
H1 (X1, U1) = ╣(H (X, U), uf, uk, ut).
Содержательно-формальное описание выполнения операции над ультраграфом HU (X, U).
Для получения ультраграфа HU1 (X1, U1):
1. Копируем множество X под именем X1: X1 = X.
2. Формируем множество рёбер U1, исключая из множества U рёбра uf и uk и добавляя в него ребро ut: U1 = {U \ {uf, uk} · ut}.
3. Получаем множество образов вершин Г1X1, занося в него Г1xi из множества Г1X, если рёбра uf и uk не инцидентны вершине xi, в противном случае:
– удаляя из Г1xi ребро uf и добавляя ребро ut, если вершине xi инцидентно ребро uf,
– удаляя из Г1xi ребро uk и добавляя ребро ut, если вершине xi инцидентно ребро uk,
– удаляя из Г1xi рёбра uf и uk и добавляя ребро ut, если оба ребра инцидентны этой вершине:
Г1X1 = {Г1xi ∕ xi Î X1}, здесь
ìГ1xi, если xi Ï Г1uf & xi Ï Г1uk,
çГ1xi \ uf · ut, если xi Î Г1uf & xi Ï Г1uk,
Г1xi = íГ1xi \ uk · ut, если xi Î Г1uk & xi Ï Г1uf,
îГ1xi \ {uf, uk} · ut, если xi Î Г1uk & xi Î Г1uf,
где Г1xi Î Г1X, Г1uf, Г1uk Î Г1U.
Приведенные для Г1xi выражения очевидны и просты для понимания. Однако их целесообразно записать в более компактном виде, а именно:
ìГ1xi : xi Ï Г1uf & xi Ï Г1uk,
Г1xi = í
îГ1xi \ {uf, uk} · ut : xi Î {Г1uf È Г1uk}.
В дальнейшем аналогичные по смыслу выражения будем записывать таким же образом.
4. Формируем множество прообразов вершин Г2X1, занося в него Г2xi из множества Г2X, если рёбра uf и uk не являются рёбрами, которым инцидентна вершина xi, в противном случае:
– удаляя из Г2xi ребро uf и добавляя ребро ut, если ребру uf инцидентна вершина xi,
– удаляя из Г2xi ребро uk и добавляя ребро ut, если ребру uk инцидентна эта вершина,
– удаляя из Г2xi рёбра uf и uk и добавляя ребро ut, если вершина инцидентна этим рёбрам:
Г2X1 = {Г2xi ∕ xi Î X1}, здесь
ìГ2xi : xi Ï Г2uf & xi Ï Г2uk,
Г2xi = í
îГ2xi \ {uf, uk} · ut : xi Î {Г2uf È Г2uk},
где Г2xi Î Г2X, Г2uf, Г2uk Î Г2U.
5. Формируем множество образов и прообразов рёбер Г2U1 и Г1U1, копируя их из Г2U и Г1U, исключая при этом Г2uf, Г2uk и Г1uf, Г1uk и добавляя образ Г2ut и прообраз Г1ut нового ребра ut соответственно:
Г2U1 = {Г2U \ {Г2uf, Г2uk} · Г2ut},
где Г2ut = Г2uf È Г2uk, Г2uf и Г2uk Î Г2U;
Г1U1 = {Г1U \ {Г1uf, Г1uk } · Г1ut},
где Г1ut = Г1uf È Г1uk, Г1uf и Г1uk Î Г1U.
6. Создаем множество образов F1X1 вершин X1 относительно предиката смежности F1(X1, X1),
– копируя образ F1xi из F1X, если вершине xi не инцидентны рёбра uf и uk или инцидентны оба,
– определяя образ вершины как объединение её образа F1xi Î F1X и множества Г2uk Î Г2U вершин, которые инцидентны ребру uk, если вершине xi инцидентно ребро uf,
– объединяя её образ и множество Г2uf Î Г2U вершин, которые инцидентны ребру uf, если вершине xi инцидентно ребро uk:
F1X1 = {F1xi ∕ xi Î X1}, где
ìF1xi : xi Ï Г1uf & xi Ï Г1uk Ú xi Î Г1uf & xi Î Г1uk,
F1xi = íF1xi È Г2uk : xi Î Г1uf,
îF1xi È Г2uf : xi Î Г1uk,
где F1xi Î F1X, Г1uf и Г1uk Î Г1U, Г2uf и Г2uk Î Г2U.
7. Получаем множество прообразов F1-1X1 вершин X1 относительно предиката смежности F1(X1, X1),
– копируя прообраз F1-1xi из F1-1X, если вершина xi не инцидентна рёбрам uf и uk или инцидентна тому и другому,
– определяя прообраз вершины как объединение её прообраза F1-1xi Î F1-1X и множества Г1uk Î Г1U вершин, которым инцидентно ребро uk, если вершина xi инцидентна ребру uf,
– объединяя её прообраз и множество Г1uf Î Г1U вершин, которым инцидентно ребро uf, если вершина xi инцидентна ребру uk:
F1-1X1 = {F1-1xi ∕ xi Î X1 }, где
ì F1-1xi: xi ÏГ2uf & xi Ï Г2uk Ú xi ÎГ2uf & xi Î Г2uk,
F1-1xi = í F1-1xi È Г1uk : xi Î Г2uf,
î F1-1xi È Г1uf : xi Î Г2uk,
где F1-1xi Î F1-1X, Г2uf и Г2uk Î Г2U, Г1uf и Г1uk Î Г1U.
8. Формируем множество образов F2U1 рёбер U1 относительно предиката смежности F2(U1, U1). При j ¹ t:
– копируя F2uj из множества F2U, если ребру uj не смежны рёбра uf и uk,
– удаляя из F2uj Î F2U ребро uf или ребро uk, если ребру uj смежно ребро uf или uk соответственно, и добавляя ребро ut,
– удаляя из F2uj Î F2U рёбра uf и uk и добавляя ребро ut, если ребру uj смежны рёбра uf и uk,:
F2U1 = { F2uj ∕ uj Î U1}, здесь
ìF2uj : uf Ï F2uj & uk Ï F2uj,
F2uj = í
îF2uj \ {uf, uk} · ut : uf Î F2uj Ú uk Î F2uj,
где F2uj Î F2U.
Образ ребра ut будет:
F2ut = {F2uf È F2uk}, если uf и uk не смежны, и F2ut = {F2uf È F2uk} \ {uf, uk} · ut, если они смежны, т. е. uf Î F2uk Ú uk Î F2uf Ú uf Î F2uk & uk Î F2uf.
9. Создаем множество F2-1U1 прообразов ребер U1. При j ¹ t:
– копируя F2-1uj из множества F2-1U, если ребро uj не смежно ни ребру uf , ни ребру uk,
– удаляя из F2-1uj Î F2-1U ребро uf или ребро uk, если ребро uj смежно ребру uf или uk соответственно, и добавляя ребро ut,
– удаляя из F2-1uj Î F2-1U рёбра uf и uk и добавляя ребро ut, если ребро uj смежно рёбрам uf и uk:
F2-1U1 = {F2-1uj ∕ uj Î U1}, здесь
ìF2-1uj : uf Ï F2-1uj & uk Ï F2-1uj,
F2-1uj = í
îF2-1uj \ {uf, uk} · ut : uf Ï F2-1uj Ú uk Ï F2-1uj,
где F2-1uj Î F2-1U.
Прообраз ребра ut будет:
F2-1ut = {F2-1uf È F2-1uk}, если рёбра uf и uk не смежны, и
F2-1ut = {F2-1uf È F2-1uk} \ {uf, uk} · ut, если они смежны.
Формальное описание операции над гиперграфом H (X, U).
Множества гиперграфа H1 (X1, U1) определяются как:
X1 = X ; U1 = {U \ {uf, uk} · ut};
Г1X1 = {Г1xi : xi ÏГ2uf & xi Ï Г2uk Ú Г1xi \ {uf, uk} · ut : xi Î {Г2uf È Г2uk} ∕ xi Î X1, Г1xi Î Г1X, Г2uf, Г2uk Î Г2U};
Г2U1 = {Г2U \ {Г2uf, Г2uk} · Г2ut}, где Г2ut = Г2uf È Г2uk, Г2uf и Г2uk Î Г2U;
F1X1 = {F1xi ∕ xi Î X1}, здесь
ìF1xi : xi Ï Г2uf & xi Ï Г2uk Ú xi Î Г2uf & xi Î Г2uk,
F1xi = íF1xi È Г2uk : xi Î Г2uf,
îF1xi È Г2uf : xi Î Г2uk,
где F1xi Î F1X, Г2uf и Г2uk Î Г2U.
F2U1 = {F2uj ∕ uj Î U1}, здесь для j ¹ t
ìF2uj : uf Ï F2uj & uk Ï F2uj,
F2uj = í
îF2uj \ {uf, uk} · ut : uf Î F2uj Ú uk Î F2uj,
где F2uj Î F2U.
Образ ребра ut будет:
ì{F2uf È F2uk} : uf Ï F2uk & uk Ï F2uf,
F2ut = í
î{F2uf È F2uk} \ {uf, uk} : uf Î F2uk (uk Î F2uf).
С процедурной точки зрения образ ребра ut целесообразно определять по формуле:
F2ut = {F2uf È F2uk} \ {uf, uk} (смотри примечание 1 в операции «удаление вершины»).
Асимптотическая оценка вычислительной сложности данной операции над ультра- и гиперграфом такая же, как и операции добавления ребра.
Операция может выполняться над куском ультра- или гиперграфа. Если оба стягиваемые ребра внутренние, то в п. 2 определяется
U1кint = {Uкint \ {uf, uk} · ut} и U1кext = Uкext.
Если хотя бы одно из этих рёбер является внешним, должна быть задана информация о виде заменяющего ребра и соответствующим образом сформированы U1кint и U1кext.
Пример. Выполним соединение цепей с1 и с2 в цепь с4 в схеме, показанной на рис. 7, а. В результате операции HU1 (X1, U1) = ╣(HU (X, U), uf, uk, ut) стягивания ребер u1 и u2 ультраграфа схемы, изображенной на рис. 7, б, получим
X1 = {x1, x2,. . . , x6};
U1 = U \ {u1, u2} · u5} = {u3, u4, u5};
Г1X1: Г1x1 = {u1} \ {u1, u2} · u5 = {u5}, Г1x2 = {u2} \ {u1, u2} · u5 = {u5}, Г1x3 = Æ; Г1x4 = {u2} \ {u1, u2} · u5 = {u5}, Г1x5 = {u2, u4} \ {u1, u2} · u5 = {u4, u5}, Г1x6 = {u3};
Г2X1: Г2x1 = Æ, Г2x2 = {u1} \ {u1, u2} · u5 = {u5}, Г2x3 = {{u1, u2} \ {u1, u2} · u5} = {u5}, Г2x4 = Æ, Г2x5 = {u3} Г1x6 = {u4};
Г1U1 = {Г1u3, Г1u4, Г1u5}, где Г1u5 = {x1} È {x2, x4, x5} = {x1, x2, x4, x5};
Г2U1 = {Г2u3, Г2u4, Г2u5}, где Г2u5 = {x2, x3} È {x2, x3} = {x2, x3};
F1X1: F1x1 = {x2, x3} È {x3} = {x2, x3}, F1x2 = {x3} È {x2, x3} = {x3, x2}, F1x3 = Æ, F1x4 = {x3} È {x2, x3} = {x3, x2}, F1x5 = {x3, x6} È {x2, x3} = {x3, x6, x2}, F1x6 = {x5};
F1-1X1: F1-1x1 = Æ, F1-1x2 = {x1} È {x2, x4, x5} = {x1, x2, x4, x5}, F1-1x3 = {x1, x2, x4, x5}, F1-1x4 = Æ, F1-1x5 = {x6}, F1-1x6 = {x5};
F2U1: F2u3 = {u2, u4} \ {u1, u2}} · u5 = {u4, u5}, F2u4 = {u3}, F2u5 = {u5};
F2-1U1: F2-1u3 = {u4}, F2-1u4 = {u3}, F2-1u5 = {u5}.
Для гиперграфа той же схемы, представленного на рис. 7, в, после операции H1 (X1, U1) = ╣(H (X, U), uf, uk, ut) получим:
X1 = {x1, x2,. . . , x6};
U1 = U \ {u1, u2} · u5} = {u3, u4, u5};
Г1X1: Г1x1 = {u1} \ {u1, u2} · u5 = {u5}, Г1x2 = Г1x3 = {u1,u2} \ {u1,u2} · u5 = {u5}, Г1x4 = {u2} \ {u1,u2} · u5 = {u5}, Г1x5 = {u2, u3, u4} \ {u1,u2} · u5 = {u3, u4, u5}, Г1x6 = {u3, u4};
Г2U1 = {Г2u3, Г2u4, Г2u5}, где Г2u5 = {x1, x2, x3} È {x2, x3, x4, x5} = {x1, x2, x3, x4, x5};
F1X1: F1x1 = {x2, x3} È {x2, x3, x4, x5} = {x2, x3, x4, x5}, F1x2 = {x1, x3, x4, x5}, F1x3 = {x1, x2, x4, x5}, F1x4 = {x1, x2, x3, x5}, F1x5 = {x2, x3, x4} È {x6} = {x2, x3, x4, x6}, F1x6 = {x5}.
F2U1: F2u3 = {u2, u4} \ {u1, u2}} · u5 = {u4, u5}, F2u4 = {u2, u3} \ {u1, u2} · u5 = {u3, u5}, F2u5 = {{u2} È {u1, u3, u4}} \ {u1, u2} = {u3, u4}.
Подразбиение ребра uk ультраграфа HU или гиперграфа H – рис. 8. Соответствует проектной операции разрыва цепи и подключения двух новых к вводимому элементу.

Рисунок 8 – Исходная схема до и после введения элемента э7 в цепь с1 (а), ее модель в виде ультраграфа HU и результат HU1 выполнения операции подразбиения ребра u1 (б), гиперграф схемы H и результат той же операции H1 (в)
Осуществляется введением вершины, образуются два новых ребра ur и ut. Задаются разбиваемое ребро uk, вводимая вершина xf, имена новых ребер ur и ut, а также:
· для ультраграфа указываются: ребро, инцидентное вершине xf, и ребро, которому она инцидентна, например, Г1xf = ur и Г2xf = ut; Xr+ = Г2ur и Xt+ = Г2ut – вершины, инцидентные ребрам ur и ut соответственно; Xr– = Г1ur и Xt– = Г1ut – вершины, которым инцидентны указанные ребра;
· для гиперграфа указываются подмножества Xr = Г2ur и Xt = Г2ut вершин, инцидентных ребрам ur и ut.
Обозначение операции:
╠ (HU (X, U), uk, xf, ur, Xr+, Xr–, ut, Xt+, Xt–)для ультраграфа и
╠ (H (X, U), uk, xf, ur, Xr, ut, Xt) для гиперграфа.
Условие корректности операции:
· для ультраграфа – uk Î U; Xr+ Ç Xt+ = Æ; Xr+ È Xt+ = Г2uk · xf ; Xr– Ç Xt– = Æ; Xr– È Xt– = Г1uk · xf; Xr+ Ç Xt– Ú Xr– Ç Xt+ = xf;
· для гиперграфа – uk Î U, Xr È Xt = Г2uk · xf; Xr Ç Xt = xf.
В результате выполнения операции получаем:
– ультраграф HU1 (X1, U1) = ╠ (HU (X, U), uk, xf, ur, Xr+, Xr–, ut, Xt+, Xt–) или
– гиперграф H1 (X1, U1) = ╠ (H (X, U), uk, xf, ur, Xr, ut, Xt).
Содержательно-формальное описание выполнения операции
над ультраграфом HU (X, U).
Для получения ультраграфа HU1 (X1, U1):
1. Определяем множество X1, добавляя в X вершину xf: X1 = X · xf.
2. Формируем множество рёбер U1, исключая из множества U ребро uk и добавляя в него рёбра ur и ut: U1 = U \ uk · {ur, ut}.
3. Получаем множество образов Г1X1, копируя Г1xi из множества Г1X, если ребро uk не инцидентно вершине xi. Если вершине xi инцидентно одно из новых рёбер, то из ее образа в Г1X исключаем ребро uk и добавляем то, которое ей инцидентно в соответствии с исходными данными операции, т. е. ur или ut. Образ вводимой вершины xf – Г1xf:
Г1X1 = {Г1xi ∕ xi Î X1}, где
ìГ1xi Î Г1X : xi Ï Г1uk, где Г1uk Î Г1U,
çГ1xi \ uk · ur : xi Î Г1ur, где Г1xi Î Г1X,
Г1xi = íГ1xi \ uk · ut : xi Î Г1ut, где Г1xi Î Г1X,
îГ1xf : xi = xf.
4. Формируем множество прообразов Г2X1, копируя Г2xi из множества Г2X, если вершина не инцидентна ребру uk. Если вершина инцидентна одному из новых рёбер, то из ее прообраза в Г2X исключаем ребро uk и добавляем то, которому она инцидентна. Прообраз вводимой вершины xf – Г2xf:
Г2X1 = {Г2xi ∕ xi Î X1}, где
ìГ2xi Î Г2X : xi Ï Г2uk, где Г2uk Î Г2U,
÷Г2xi \ uk · ur : xi Î Г2ur, где Г2xi Î Г2X,
Г2xi = íГ2xi \ uk · ut : xi Î Г2ut, где Г2xi Î Г2X,
îГ2xf : xi = xf.
5. Создаем множества образов Г2U1 и прообразов Г1U1 рёбер, копируя их из Г2U и Г1U1, исключая при этом Г2uk и Г1uk и добавляя в соответствующие множества образы и прообразы новых рёбер ur и ut:
Г2U1 = Г2U \ Г2uk · {Г2ur, Г2ut}, где Г2ur = Xr+, Г2ut = Xt+;
Г1U1 = Г1U \ Г1uk · {Г1ur, Г1ut}, где Г1ur = Xr–, Г1ut = Xt–.
6. Определяем множество образов F1X1 вершин X1 для чего для xi ¹ xf:
– копируем F1xi из F1X, если вершине xi не инцидентно ребро uk,
– удаляем из F1xi множество вершин, инцидентных ребру uk, и добавляем множество вершин, инцидентных ребру ur, если вершине xi инцидентно ребро ur,
– удаляем из F1xi множество вершин, инцидентных ребру uk, и добавляем множество вершин, инцидентных ребру ut, если вершине xi инцидентно это ребро.
При xi = xf записываем в F1xf множество вершин, инцидентных ребру ur, если оно инцидентно вводимой вершине, или ребру ut, если данное ребро инцидентно этой вершине:
F1X1 = {F1xi ∕ xi Î X1}, здесь для i ¹ f
ìF1xi Î F1X : xi Ï Г1uk, где Г1uk Î Г1U,
F1xi = í{F1xi \ Г2uk} · Г2ur : xi Î Г1ur, где F1xi Î F1X,
î{F1xi \ Г2uk} · Г2ut : xi Î Г1ut, где F1xi Î F1X,
F1xf = Г2ur : Г1xf = ur Ú Г2ut : Г1xf = ut.
7. Создаем множество прообразов F1-1X1 вершин X1 для чего:
– копируем F1-1xi из F1-1X, если вершине xi не смежно ребро uk,
– удаляем из F1-1xi множество вершин, которым инцидентно ребро uk, и добавляем множество вершин, которым инцидентно ребро ur, если вершина xi инцидентна ребру ur,
– удаляем из F1-1xi множество вершин, которым инцидентно ребро uk, и добавляем множество вершин, которым инцидентно ребро ut, если вершина xi инцидентна этому ребру,
При xi = xf заносим в F1-1xf множество вершин, которым инцидентно ребро ur, если ему инцидентна вводимая вершина, или множество вершин, которым инцидентно ребро ut, если ему инцидентна вводимая вершина:
F1-1X1 = {F1-1xi ∕ xi Î X1}, здесь для i ¹ f
ìF1-1xi Î F1-1X : xi Ï Г2uk, где Г2uk Î Г2U,
F1-1xi = í{F1-1xi \ Г1uk} · Г1ur : xi Î Г2ur, где F1-1xi Î F1-1X,
î{F1-1xi \ Г1uk} · Г1ut : xi Î Г2ut, где F1-1xi Î F1-1X,
F1-1xf = Г1ur : Г2xf = ur ÚГ1ut : Г2xf = ut.
8. Формируем множество образов F2U1 ребер U1 относительно предиката смежности F2(U1, U1), для j ¹ r ¹ t:
– копируя F2uj из множества F2U, если ребро uk не смежно ребру uj,
– удаляя из F2uj Î F2U ребро uk и добавляя ребро ur, если эти рёбра смежны ребру uj,
– удаляя из F2uj Î F2U ребро uk и добавляя ребро ut, если эти рёбра смежны ребру uj,
– удаляя из F2uj Î F2U ребро uk и добавляя рёбра ur, ut , если все эти рёбра смежны ребру uj:
F2U1 = {F2uj ∕ uj Î U1}, здесь
ìF2uj : uk Ï F2uj,
ç{F2uj \ uk} · ur : uk Î F2uj & Г2uj Ç Г1ur ¹ Æ,
F2uj = í{F2uj \ uk} · ut : uk Î F2uj & Г2uj Ç Г1ut ¹ Æ,
î{F2uj \ uk} · {ur, ut} : uk Î F2uj & Г2uj Ç Г1ur ¹ Æ & Г2uj Ç Г1ut ¹ Æ, где F2uj Î F2U.
Рёбра, смежные рёбрам ur и ut, определяются по формулам:
F2ur = È Г1xi и F2ut = È Г1xi, Г1xi Î Г1X.
xi Î Г2u xi Î Г2ut
9. Определяем множество прообразов F2-1U1 рёбер множества U1 относительно предиката смежности F2 (U1, U1), для j ¹ r ¹ t:
– копируя F2-1uj из множества F2-1U, если ребру uk не смежно ребро uj,
– удаляя из F2-1uj Î F2-1U ребро uk и добавляя ребро ur, если этим ребрам смежно ребро uj,
– удаляя из F2-1uj Î F2-1U ребро uk и добавляя ребро ut, если этим ребрам смежно ребро uj,
– удаляя из F2-1uj Î F2-1U ребро uk и добавляя ребра ur, ut , если всем этим ребрам смежно ребро uj:
F2-1U1 = {F2-1uj ∕ uj Î U1}, здесь
ì F2-1uj : uk Ï F2-1uj,
ç{F2-1uj \ uk}· ur : uk Î F2-1uj & Г1uj Ç Г2ur ¹ Æ,
F2-1uj = í{F2-1uj \ uk} · ut : uk Î F2-1uj & Г1uj Ç Г2ut ¹ Æ,
î{F2-1uj \ uk} · {ur, ut} : uk Î F2-1uj & Г1uj Ç Г2ur ¹ Æ & Г1uj Ç
Г2ut ¹ Æ, где F2-1uj Î F2-1U.
Прообразы рёбер ur и ut определяются по формулам:
F2-1ur = È Г2xi и F2-1ut = È Г2xi, Г2xi Î Г2X.
xi Î Г1ur xi Î Г1ut
Формальное описание выполнения операции над гиперграфом.
Множества гиперграфа H1 (X1, U1) получаем по выражениям:
X1 = X · xf; U1 = U \ uk · {ur, ut};
Г1X1 = (Г1xi ∕ xi Î X1}, где Г1xf = {ur, ut} и для i ¹ f
ìГ1xi Î Г1X, если uk Ï Г1xi,
Г1xi = íГ1xi \ uk · ur, если ur Î Г1xi, где Г1xi Î Г1X,
îГ1xi \ uk · ut, если ut Î Г1xi, где Г1xi Î Г1X;
Г2U1 = Г2U \ Г2uk · {Г2ur, Г2ut}, где Г2ur = Xr, Г2ut = Xt;
F1X1 = {F1xi ∕ xiÎX1}, здесь F1xf = Xr · Xt \ xf и для i ¹ f
ìF1xi Î F1X : xi Ï Г2uk, где Г2uk Î Г2U,
F1xi = í{F1xi · Г2ur }\ Г2uk : xi Î Г2ur, где F1xi Î F1X,
î{F1xi · Г2ut} \ Г2uk : xi Î Г2ut, где F1xi Î F1X;
F2U1 = {F2uj ∕ uj Î U1}, здесь для j ¹ r ¹ t
ì F2uj : uk Ï F2uj,
ç{F2uj \ uk} · ur : uk Î F2uj & Г2uj Ç Г2ut = Æ,
F2uj = í{F2uj \ uk}· ut : uk Î F2uj & Г2uj Ç Г2ur = Æ,
î{F2uj \ uk} · {ur, ut} : uk Î F2uj & Г2uj Ç Г2ur ¹ Æ & Г2uj Ç Г2ut ¹ Æ, где F2uj Î F2U.
Рёбра, смежные ребрам ur и ut, определяются по формулам:
F2ur = È {Г1xi \ ur : |Г2ur| > 1 Ú Г1xi : |Г2ur| = 1},
xi Î Г2ur
F2ut = È {Г1xi \ ut : | Г2ut| > 1 Ú Г1xi : |Г2ut| = 1}.
xi Î Г2ut
Асимптотическая оценка вычислительной сложности данной операции над ультра- и гиперграфом такая же, как и операции добавления ребра.
Операция может быть распространена на кусок ультра- или гиперграфа. Если разбиваемое ребро является внешним, должна быть задана информация о виде новых рёбер и соответствующим образом сформированы U1кint и U1кext.
Пример. Выполним подразбиение ребра для варианта модификации схемы, показанного на рис. 8, а. Тогда для операции подразбиения ребра ультраграфа (смотри рис. 8, б) uk = u1, xf = x7, ur = u3, ut = u4 и Г1x7 = {u4}, Г2x7 = {u3}, Г2u3 = {x2, x7}, Г2u4 = {x3, x4}, Г1u3 = {x1}, Г1u4 = {x7}.
В результате выполнения HU1 (X1, U1) = ╠ (HU (X, U), uk, xf, ur, ut) операции получим ультраграф HU1, у которого:
X1 = X · x7 = {x1, x2, …, x7}; U1 = U \ u1 · {u3, u4} = {u2, u3, u4};
Г1X1: Г1x1 = {u1} \ {u1} · u3 = {u3}, Г1x2 = Г1x4 = Г1x5 = Г1x6 = Æ,
Г1x3 = {u2}, Г1x7 = {u4};
Г2X1: Г2x1 = Æ, Г2x2 = {u1} \ {u1} · u3 = {u3}, Г2x3 = {u1} \ {u1} · u4 = {u4}, Г2x4 = {u1} \ {u1} · u4 = {u4}, Г2x5 = {u2}, Г2x6 = {u2}, Г1x7 = {u3};
Г2U1 = {Г2u2, Г2u3, Г2u4}, где: Г2u2 = {x5, x6}, Г2u3 = {x2, x7}, Г2u4 = {x3, x4};
Г1U1 = {Г1u2, Г1u3, Г1u4}, где: Г1u2 = {x3}, Г1u3 = {x1}, Г1u4 = {x7};
F1X1: F1x1 = {x2, x3, x4} \ {x2, x3, x4} · {x2, x7} = {x2, x7}, F1x2 = F1x4 = F1x5 = F1x6 = Æ, F1x3 = {x5, x6}, F1x7 = Г2u4 = {x3, x4};
F1-1X1 : F1-1x1 = Æ , F1-1x2 = {x1}, F1-1x3 = F1-1x4 = {x7}, F1-1x5 = F1-1x6 ={x3}, F1-1x7 = Г1u3 = {x1};
F2U1: F2u2 = Æ, F2u3 = È Г1xi = Г1x2 È Г1x7 = {u4}, F2u4 = È Г1xi =
xi Î Г2u3 xi Î Г2u4
Г1x3 È Г1x4 = {u2};
F2-1U1: F2-1u2 = {u1} \ {u1} · {u4} = {u4}, F2-1u3 = Г2x1 = Æ,
F2-1u4 = Г2x7 = {u3}.
Для гиперграфа показанного на рис. 8, в, операция H1 (X1, U1, Г1X1, Г2U1) =╠ (H (X, U, Г1X, Г2U), uk, xf, ur, ut) подразбиения ребра u1 на рёбра u3 и u4 введением вершины xf = x7 так, что X3 = Г2u3 = {x1, x2, x7} и X4 = Г2u4 = {x3, x4, x7}, дает гиперграф H1, у которого:
X1 = {x1, x2, …, x7}; U1 = {u2, u3, u4};
Г1X1: Г1x1 = Г1x2 = {{u1 \ u1} · u3} = {u3}, Г1x3 = {{{u1, u2} \ u1} · u4} = {u2, u4}, Г1x4 = {{{u1} \ u1} · u4} = {u4}, Г1x5 = Г1x6 = {u2}, Г1x7 = {u3, u4};
Г2U1 = {Г2u2, Г2u3, Г2u4}, где: Г2u2 = {x3, x5, x6}, Г2u3 = {x1, x2, x7},
Г2u4 = {x3, x4, x7}.
Удаление вершины xk из образов и прообразов ребер ультраграфа HU или образов ребер гиперграфа H – рис. 9. Реализует проектную опера-цию отключения элемента схемы эk от множества цепей Сt.

Рисунок 9 – Фрагмент схемы до и после отключения элемента Э3 от цепей с1 и с2 (а), модель схемы в виде ультраграфа HU и результат операции HU1 (б), модель схемы в виде гиперграфа H и результат операции в виде гиперграфа H1и куска H1к (в)
Задается имя удаляемой вершины xk и:
· для ультраграфа – подмножество Uk' инцидентных ей ребер, из прообразов которых следует удалить вершину xk, и подмножество Uk² ребер, которым инцидентна эта вершина и из чьих образов её надо удалить;
· для гиперграфа – подмножество Uk' инцидентных вершине xk ребер, из образов которых её следует удалить.
Обозначение операции: HU (X, U) : {Г1Uk', Г2Uk²}\ xk для ультраграфа и
H(X, U) : Г2Uk' \ xk для гиперграфа.
Условия корректности операции:
– для ультраграфа xk Î X, Uk' Í Uk+ & Uk² Ì Uk– Ú Uk² Í Uk– & Uk' Ì Uk+ Ú Uk' Ì Uk+ & Uk²Ì Uk– , где Uk+ = Г1xk, Uk– = Г2xk;
– для гиперграфа xk Î X, Uk' Ì Г1xk.
При применении операции образуется одна компонента связности, если xk не является вершиной, расщепляющей граф в отношении ребер множества {Uk' È Uk²} для ультраграфа и Uk' для гиперграфа. В противном случае граф распадается на компоненты связности и при преобразовании графа необходимо определять компоненты связности и множества их вершин.
Если xk не является расщепляющей вершиной, в результате выполнения операции получаем:
– ультраграф HU1 (X1, U1) = HU (X, U) : {Г1Uk' , Г2Uk²} \ xk , если
" uj Î{Uk' È Uk²} (|Г2uj| + |Г1uj| > 2), (8)
– кусок ультраграфа HU1к (X1к, U1к) = HU (X, U) : {Г1Uk', Г2Uk²} \ xk, если
$ uj Î {Uk' È Uk²} (|Г2uj| + |Г1uj| = 2), (9)
– гиперграф H1 (X1, U1) = H (X, U) : {Г2Uk' }\ xk, если
" ul Î Uk' (|Г2ul| > 2), (10)
– кусок гиперграфа H1к (X1к, U1к) = H (X, U) : {Г2Uk'} \ xk, если
$ ul Î Uk' (|Г2ul| = 2). (11)
Содержательно-формальное описание выполнения операции
над ультраграфом при справедливости условия (8).
Для получения множеств ультраграфа HU1 (X1, U1):
1. Копируем множества X и U под именами X1 и U1 соответственно:
X1=X ; U1= U.
2. Формируем множество образов вершин Г1X1, копируя их из множества Г1X, если i ¹ k. Из образа Г1xk удаляем ребра множества Uk':
Г1X1 = {Г1xi : i ¹ k Ú Г1xi \ Uk' : i = k ∕ xi Î X1, Г1xi Î Г1X}.
3. Создаем множество прообразов вершин Г2X1, копируя их из множества Г2X1, если i ¹ k. Из прообраза Г2xk удаляем ребра множества Uk²:
Г2X1 = {Г2xi : i ¹ k Ú Г2xi \ Uk² : i = k ∕ xi Î X1, Г2xi ÎГ2X}.
4. Формируем множество образов ребер Г2U1, копируя их из Г2U и удаляя при этом вершину xk из образов ребер множества Ut–:
Г2U1 = {Г2uj : uj Î Uk²Ú Г2uj \ xk : uj Î Uk² ∕ uj Î U1, Г2uj Î Г2U}.
5. Определяем множество прообразов ребер Г1U1, копируя их из Г1U и удаляя при этом вершину xk из прообразов ребер множества Uk':
Г1U1 = {Г1uj : uj Î Uk' Ú Г1uj \ xk : uj Î Uk' ∕ uj Î U1, Г1uj Î Г2U}.
6. Создаем множество F1X1 образов вершин X1 относительно предиката смежности F1(X1, X1) для чего при i ¹ k:
– копируем F1xi из F1X, если вершина xk не была смежна вершине xi или была и остается смежной после её удаления из образов ребер Uk²,
– удаляем из образа F1xi вершину xk, если она становится не смежной xi после её удаления из образов ребер Uk².
Образ F1xk вершины xk получаем как объединение образов Г2uj ребер, инцидентных этой вершине после удаления из её образа Г1xk множества ребер Uk':
F1X1 = {F1xi ∕ xi Î X1}, где при i ¹ k:
ìF1xi : xk Ï F1xi Ú xk Î F1xi & Г1xi Ç {Г2xk \ Uk²} ¹ Æ,
F1xi = í
îF1xi \ xk : xk Î F1xi & Г1xi Ç {Г2xk \ Uk²} = Æ,
здесь: F1xi Î F1X, Г1xi Î Г1X, Г2xk Î Г2X.
F1xk = È Г2uj, где Г1xk Î Г1X, Г2uj Î Г2U.
uj Î Г1xk \ Uk'
Например (смотри рис. 9, б), вершина x3 осталась бы смежной вершине x1 после удаления x3 из образа Г2u1 ребра u1, т. е. F1x1 = {x2, x3}, если бы существовало ребро u5, показанное на рисунке точками. Так как в схеме нет цепи с5 « u5, то после удаления вершины x3 из образа Г2u1 условие
Г1x1 Ç {Г2x3 \ u1} = Æ выполняется и F1x1 = {x2, x3}\ x3 = {x2}.
7. Создаем множество F1-1X1 прообразов вершин X1, для чего при i ¹ k:
– копируем F1-1xi из F1-1X, если вершине xk не была смежна вершина xi или была и остается смежной после её удаления из образов ребер Uk',
– удаляем из прообраза F1-1xi вершину xk, если этой вершине была и остается смежной вершина xi после удаления xk из прообразов ребер Uk'.
Прообраз F1-1xk вершины xk получаем как объединение образов Г1uj ребер, которые инцидентны этой вершине после удаления из её образа Г1xk множества ребер Uk²:
F1-1X1 = {F1-1xi ∕ xi Î X1}, где при i ¹ k:
ìF1-1xi : xk Ï F1-1xi Ú xk Î F1-1xi & Г2xi Ç { Г1xk \ Uk'} ¹ Æ,
F1-1xi = í
îF1-1xi \ xk : xk Î F1-1xi & Г2xi Ç { Г1xk \ Uk'} = Æ,
здесь: F1-1xi Î F1-1X, Г2xi Î Г2X, Г1xk Î Г1X.
F1-1xk = È Г1uj, где Г2xk Î Г2X, Г1uj Î Г1U.
uj Î Г2xk \ Uk²
8. Формируем множество образов F2U1 ребер U1 относительно предиката смежности F2(U1, U1):
– копируя F2uj из множества F2U, если ребру uj не инцидентна вершина xk, либо была и остается инцидентной, но не удаляется из прообразов смежных ей ребер,
– получая F2uj как объединение ребер, инцидентных вершинам множества Г2uj \ xk, если ребро uj удаляется из прообраза Г2xk вершины xk, т. е. вершина становится не смежной ему,
– определяя F2uj как объединение множества ребер, полученного по предыдущему правилу, и ребер, инцидентных вершине xk без множества Uk', если ребро uj не принадлежит множеству ребер, из образов которых удаляется вершина xk, т. е. эта вершина в результате выполнения операции остается инцидентной ребру uj и множество ребер, из прообразов которых удаляется вершина xk, не пусто:
F2U1 = {F2uj ∕ uj Î U1}, здесь
ì F2uj : uj Ï Г2xk Ú uj Î Г2xk \ Uk² & Uk' = Æ,
F2uj = í È Г1xi : uj Î Uk²,
xi Î Г2uj \ xk
î {È Г1xi} È {Г1xk \ Uk'} : uj Ï Uk² & Uk' ¹ Æ,
xi Î Г2uj \ xk
где F2uj Î F2U, Г2xk Î Г2X, Г2uj Î Г2U, Г1xi , Г1xk Î Г1X.
9. Формируем множество прообразов F2-1U1 ребер U1 относительно предиката смежности F2(U1,U1):
– копируя F2-1uj из множества F2-1U, если ребро uj не инцидентно вершине xk,
– удаляя из F2-1uj Î F2-1U множество ребер Uk², если ребро uj было и остается инцидентным вершине xk,
– удаляя из F2-1uj Î F2-1U множество ребер, которым инцидентна вершина xk, если ребро uj принадлежит множеству ребер, из прообразов которых удаляется вершина xk, т. е. этой вершине в результате выполнения операции становится не инцидентно ребро uj:
F2-1U1 = {F2-1uj ∕ uj Î U1}, здесь
ìF2-1uj : uj Ï Г1xk Ú uj Î Г1xk \ Uk' & Uk² = Æ,
F2-1uj = í È Г2xi : uj Î Uk',
xi Î Г1uj \ xk
î {È Г2xi} È {Г2 xk \ Uk²} : uj Ï Uk' & Uk² ¹ Æ,
xi Î Г1uj \ xk
где F2-1uj Î F2-1U, Г1xk Î Г1X, Г2xi, Г2xk Î Г2X, Г1uj Î Г1U .
Для куска ультраграфа HU1к дополнительно формируем множество внешних ребер U1кext, в него включаем те из ребер множества Ut, для которых после выполнения операции сумма количества вершин, инцидентных ему, и количества вершин, которому оно инцидентно, равна единице. Определяем также множество внутренних ребер куска U1кint, исключая из U1к внешние.
При выполнении условия (9), получаем кусок ультраграфа HU1к. Множества X1к, U1к, Г1X1к, Г2X1к, Г2U1к, Г1U1к, F1X1к, F1-1X1к, F2U1к, F2-1U1к определяются по тем же формулам, что и множества ультраграфа HU1 (X1, U1). Множество ребер U1к разбивается на подмножества U1кint и U1кext, такие, что
U1кext = {uj Î { Uk² È Uk' }:(|Г2uj| + |Г1uj|) = 1 ∕ Г2uj Î Г2U1, Г1uj Î Г1U1};
U1кint = U1к \ U1кext.
Формальное описание операции над гиперграфом H (X, U).
При выполнении условия (10) получаем гиперграф H1 (X1, U1):
X1 = X; U1 = U;
Г1X1 = {Г1xi : i ¹ k Ú Г1xi \ Uk' : i = k ∕ xi Î X1, Г1xi Î Г1X};
Г2U1 = {Г2uj : uj Î Uk' Ú Г2uj \ xk : uj Î Uk' ∕ uj Î U1, Г2uj Î Г2U};
F1X1 = {F1xi ∕ xi Î X1}, где при i ¹ k:
ìF1xi : xk Ï F1xi Ú xk Î F1xi & Г1xi Ç { Г1xk \ Uk'} ¹ Æ,
F1xi = í
îF1xi \ xk : xk Î F1xi & Г1xi Ç { Г1xk \ Uk' } = Æ,
здесь: F1xi Î F1X, Г1xi, Г1xk Î Г1X,
F1xk = È{ Г2uj \ xi : | Г2uj | > 1 Ú Г2uj : | Г2uj| = 1}, где Г1xk Î Г1X, Г2uj Î Г2U;
uj Î Г1xk \ Uk'
F2U1 = {F2uj ∕ uj Î U1}, здесь
ìF2uj : uj Ï Г1xk,
F2uj = íF2uj \ ui Î Uk' : uj Î Г1xk \ Uk' & Г2uj Ç Г2ui \ xk = Æ,
îF2uj \ ui Î Г1xk \ Uk' : uj Î Uk' & Г2uj \ xk Ç Г2ui = Æ,
где F2uj Î F2U, Г1xk Î Г2X, Г2uj, Г2ui Î Г2U.
Если справедливо условие (11), получаем кусок гиперграфа H1к (X1к, U1к). Множества X1к, U1к, Г1X1к, Г2U1к , F1X1к, F2U1к формируются по тем же правилам, что и для гиперграфа H1 (X1, U1), а U1кext = {uj Î Uk' : |Г2uj| = 1 ∕ Г2uj Î Г2U1к}, U1кint = U1к \ U1кext.
Если вершина xk является расщепляющей в отношении множества рёбер {Uk' È Uk²} для ультраграфа (Uk' для гиперграфа) и определено множество вершин Xl некоторой компоненты связности, то множество её рёбер
Ul = {uj Î È{Г1xi È Г2xi} ∕ Г1xi Î Г1X, Г2xi Î Г2X},
xiÎXl
а остальные множества находим по формулам для компоненты соответствующего вида с учетом того, что xi и uj определены на множествах Xl и Ul соответственно (xi Î Xl и uj Î Ul).
Поскольку анализ вычислительной сложности данной операции несколько сложнее, чем предыдущих, приведем исходные и промежуточные данные для него по схеме: «наименование формируемого множества» : «количество операций сравнения/копирования в функции от мощности обрабатываемых множеств». Вычислительную сложность будем оценивать для операции над ультраграфом без учета получения образов и прообразов вершин и ребер ультраграфа относительно предикатов смежности F1(X1, X1) и F2(U1, U1).
X1: |X | = n; U1: |U| = m;
Г1X1: (|X| - 1) × |Г1xi| + |Г1xi| × |Uk'| + |Г1xi|;
Г2X1: (|X| -1) × |Г2xi| + |Г2xi| × |Uk²| + |Г2xi|;
Г2U1: (|Uk²| + |Г2uj|) × (|U| – |Uk²|) + (|Г2uj| + |Г2uj|) × |Uk²| = (|U| – | Uk²|) × |Uk²| + |Г2uj| × (|U| + |Uk²|);
Г1U1: (|Uk'| + |Г1uj|) × (|U| – |Uk'|) + (|Г1uj| + |Г1uj|) × |Uk'| = (|U| –
|Uk'|) × | Uk' + |Г1uj| × (|U| + |Uk'|).
Асимптотическая оценка вычислительной сложности данной операции равна:
· в худшем – О(m2) при m > n, если |Г1xi| или |Uk'| (|Г2xi| или |Uk²|) ограничены величиной m, или – О(n × m), если |Г2uj| или|Г1uj| ограничены величиной n либо |Г1xi| или |Г2xi| ограничены величиной m и n> m;
· в лучшем – О(n) при n> m и – О(m) при m > n, если мощности образов и прообразов вершин и ребер, а также |Uk'| и | Uk²| ограничены константой.
Вычислительная сложность операции над гиперграфом имеет тот же порядок.
Операция может выполняться над куском HUк (Xк, Uк) ультра- или Hк (Xк, Uк) гиперграфа. При этом среди компонент связности может появиться граф (графы) вида G®(Æ, u), если для внешних ребер куска HUк (Xк, Uк) выполняется условие
$ ujÎ {Uk' È Uk²}(|Г2uj| + |Г1uj| = 1),
или вида G~ (Æ, u), если для внешних ребер куска Hк (Xк, Uк) выполняется условие
$ ujÎ Uk' (|Г2uj| = 1).
Пример. Отключим в схеме, показанной на рис. 9, а, элемент э3 от цепей с1 и с2. Над моделью схемы в виде ультраграфа (смотри рис. 9, б) выполняется операция удаления вершины x3 из образов ребер u1 и u2, т. е. Uk' = {u2}и Uk² = {u1}. Вершина x3 не является расщепляющей и выполняется условие (8), так как |Г2u1| + |Г1u1| = 3 и |Г2u2| + |Г1u2| = 4.
В результате выполнения операции HU1 (X1, U1) = HU (X, U) : {Г1Uk', Г2Uk²} \ xk получим ультраграф HU1, у которого:
X1 = X = {x1, x3, x4, x5}; U1 = U = {u1, u2, u3, u4};
Г1X1: Г1x1 = {u1}, Г1x2 = {u4}, Г1x3 = {u2, u3} \ {u2} = {u3}, Г1x4 = Æ,
Г1x5 = {u2};
Г2X1: Г2x1 = Æ, Г2x2 = {u1, u2}, Г2x3 = {u1, u4} \ {u1} = {u4}, Г2x4 = {u2, u3}, Г2x5 = Æ;
Г2U1: Г2u1 = {x2, x3} \ x3 = {x2}, Г2u2 = {x2, x4}, Г2u3 = {x4}, Г2u4 = {x3};
Г1U1: Г1u1 = {x1}, Г1u2 = { x3, x5} \ x3 = {x5}, Г1u3 = {x3}, Г1u4 = {x2};
F1X1: F1x1 = {x2, x3} \ x3 = {x2}, F1x2 = {x3}, F1x3 = Г2u3 = {x4}, F1x4 = Æ, F1x5 = {x2, x4};
F1-1X1: F1-1x1 = Æ, F1-1x2 = {x1, x3, x5} \ x3 = {x1, x5}, F1-1x3 = Г1u4 = {x2},
F1-1x4 = {x3, x5}, F1-1x5 = Æ;
F2U1: F2u1 = Г1x2 = {u4}, F2u2 = {u4}, F2u3 = Æ, F2u4 = {u2, u3} \ {u2} = {u3};
F2-1U1: F2-1u1 = Æ, F2-1u2 = Г2{Æ} = Æ, F2-1u3 = {u1, u4} \ {u1} = {u4},
F2-1u4 = {u1, u2}.
В гиперграфе, показанном на рис. 9, в, удалим вершину x3 из образов ребер u1 и u2, т. е. Uk' = {u1, u2}. Так как |Г2u1| = 3 и |Г2u2| = 4, в результате выполнения операции
H1 (X1, U1, Г1X1, Г2U1) = H (X, U, Г1X, Г2U) : {Г2Uk' } \ xk
получаем гиперграф H1, в котором:
X1 = X = {x1, x3, x4, x5}; U1 = U = {u1, u2, u3, u4};
Г1X1: Г1x1 = {u1}, Г1x2 = {u1, u2, u4}, Г1x3 = {u1, u2, u3} \ {u1, u2} = {u3},
Г1x4 = {u2, u3, u4}, Г1x5 = {u2};
Г2U1: Г2u1 = {x1, x2, x3} \ x3 = {x1, x2}, Г2u2 = {x2, x3, x4, x5} \ x3 = {x2, x4, x5}, Г2u3 = {x3, x4}, Г2u4 = {x2, x4}.
При удалении вершины x3 из образа ребра u3 получим кусок гиперграфа H1к, в котором:
X1к = X; U1к = U; U1кext = {u3}, U1кint = {u1, u2};
Г1X1к: Г1x1 = {u1}, Г1x2 = {u1, u2, u4}, Г1x3 = {u1, u2, u3} \ {u3} = {u1, u2},
Г1x4 = {u2, u3, u4}, Г1x5 = {u2};
Г2U1: Г2u1 = {x1, x2, x3}, Г2u2 = {x2, x3, x4, x5}, Г2u3 = {x3, x4} \ x3 = {x4}, Г2u4 = {x2, x4}.
Удаление ребра uk из образов и прообразов вершин ультраграфа HU и образов вершин гиперграфа H – рис. 10. Соответствует проектной операции отключения цепи сk от заданного множества элементов схемы.
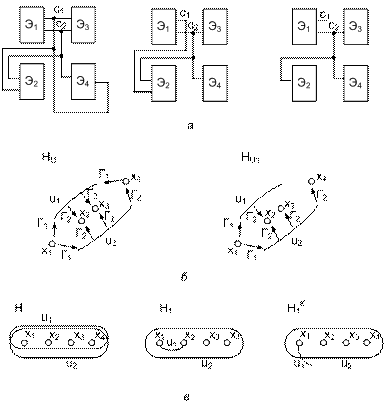
Рисунок 10 – Фрагмент схемы до и после отключения цепи с1 от элементов э3 и э4 (а), модель схемы в виде ультраграфа HU и результат операции HU1 (б), модель в виде гиперграфа H и результаты операции H1 и H1к для вариантов отключения цепи с1 от элементов э3, э4 и э2, э3, э4 (в)
Задается имя удаляемого ребра uk и:
· для ультраграфа – подмножество Xk' инцидентных ему вершин, из прообразов которых надо удалить это ребро, и подмножество Xk² вершин, которым инцидентно это ребро и из чьих образов следует его удалить;
· для гиперграфа – подмножество Xk' инцидентных ребру вершин, из образов которых оно удаляется.
Обозначение операции: HU (X, U) : {Г1Xk², Г2Xk'} \ uk для ультраграфа и
H(X, U) : Г1Xk' \ uk для гиперграфа.
Условия корректности операции:
– для ультраграфа: uk Î U, Xk' Í Г2uk и Xk² Ì Г1uk или Xk' Ì Г2uk и Xk² Í Г1uk или Xk' Ì Г2uk и Xk² Ì Г1uk;
– для гиперграфа uk Î U, Xk' Ì Г2uk.
При применении операции образуется одна компонента связности, если ни одна из вершин множества {Xk' È Xk²} в ультраграфе (Xk' в гиперграфе) не является расщепляющей и для каждой из них |Г1xi| + |Г2xi| >1 для ультраграфа и |Г1xi| > 1 для гиперграфа. В противном случае граф распадается на компоненты связности и при преобразовании графа необходимо определять компоненты связности и множества их вершин.
Если вершины множества {Xk' È Xk²} или Xk' не являются расщепляю-щими, в результате выполнения операции получаем:
– ультраграф HU1 (X1, U1) = HU (X, U) : {Г1Xk², Г2Xk'} \ uk, если
|Г2uk\ Xk'| + |Г1uk\ Xk²| ³ 2, (12)
– кусок ультраграфа HU1к (X1к, U1к) = HU (X, U) : { Г1Xk², Г2Xk'} \ uk, если
|Г2uk \ Xk'| + |Г1uk \ Xk²| = 1, (13)
– гиперграф H1 (X1, U1) = H (X, U) : Г1Xk' \ uk, если
|Г2uk \ Xk'| ³ 2 , (14)
– кусок гиперграфа H1к (X1к, U1к) = H (X, U) : Г1Xk' \ xk, если
|Г2uk \ Xk'| = 1 . (15)
Содержательно-формальное описание выполнения операции над ультраграфом HU (X, U) при справедливости условия (12).
Для получения результата – ультраграфа HU1 (X1, U1):
1. Копируем множества X и U под именами X1 и U1 соответственно:
X1 = X; U1 = U.
2. Формируем множество образов вершин Г1X1, копируя их из множества Г1X и удаляя uk из образов вершин множества Xk²:
Г1X1 = {Г1xi : xi Ï Xk² Ú Г1xi \ uk : xi Î Xk² ∕ xi Î X1, Г1xi Î Г1X}.
3. Получаем множество прообразов вершин Г2X1, копируя их из множества Г2X и удаляя uk из прообразов вершин множества Xk':
Г2X1 = {Г2xi : xi Ï Xk' Ú Г2xi \ uk : xi Î Xk' ∕ xi Î X1, Г1xi Î Г1X}.
4. Формируем множество образов ребер Г2U1, копируя их из Г2U, если j ¹ k, и удаляя из образа Г2uk вершины, принадлежащие множеству Xk':
Г2U1 = {Г2uj : j ¹ k Ú Г2uj \ Xk' : j = k ∕ uj Î U1, Г2uj Î Г2U}.
3. Создаем множество прообразов ребер Г1U1, копируя их из Г1U, если j ¹ k, и удаляя из прообраза Г1uk вершины, принадлежащие множеству Xk²:
Г1U1 = {Г1uj : j ¹ k Ú Г1uj \ Xk² : j = k ∕ uj Î U1, Г1uj Î Г1U}.
4. Определяем множество образов F1X1 для чего:
– копируем F1xi из F1X, если вершине xi не инцидентно ребро uk или было и остается инцидентным после своего удаления из образов вершин множества Xk² и при этом оно не удаляется из прообразов инцидентных ей вершин, т. е. Xk' = Æ,
– получаем F1xi как объединение множества вершин, инцидентных рёбрам образа Г1xi без ребра uk, если оно удаляется из образа вершины xi, т.е.
xi Î Xk²,
– находим F1xi как объединение множества вершин, сфомированного по предыдущему правилу, и множества вершин, инцидентных ребру uk, без множества Xk', если ребро uk не удаляется из образа вершины xi, т. е. xi Ï Xk², и Xk' ¹ Æ:
F1X1 = { F1xi ∕ xi Î X1}, где
ì F1xi : xi Ï Г1uk Ú xi Î Г1uk \ Xk² & Xk' = Æ,
F1xi = í È Г2uj : xi Î Xk²,
uj Î Г1xi \ uk
î {È Г2uj} È {Г2uk \ Xk'} : xi Ï Xk² & Xk' ¹ Æ,
uj Î Г1xi \ uk
где F1xi Î F1X, Г1uk Î Г1U, Г2uj, Г2uk Î Г2U, Г1xi Î Г1X.
5. Формируем множество прообразов F1-1X1 для чего:
– копируем F1-1xi из F1-1X, если вершина xi не инцидентна ребру uk или была и остается инцидентной после удаления ребра из прообразов вершин множества Xk' и при этом ребро не удаляется из образов вершин, которым она инцидентна, т. е. Xk² = Æ,
– получаем F1-1xi как объединение множества вершин, которым инци-дентны ребра прообраза Г2xi без ребра uk, если это ребро удаляется из прообраза вершины xi, т. е. xi Î Xk',
– находим F1-1xi как объединение множества вершин, определенного по предыдущему правилу, и множества вершин, которым инцидентно ребро uk, без множества Xk², если ребро uk не удаляется из прообраза вершины xi, т. е. xi Ï Xk', и Xk² ¹ Æ:
F1-1X1= { F1-1xi ∕ xiÎX1}, где
ì F1-1xi : xi Ï Г2uk Ú xi Î Г2uk \ Xk' & Xk² = Æ,
F1-1xi = í È Г1uj : xi Î Xk',
uj Î Г2xi\ uk
î{È Г1uj } È {Г1uk \ Xk²} : xi Ï Xk' & Xk² ¹ Æ,
uj Î Г2xi \ uk
где F1-1xi Î F1-1X, Г2uk Î Г2U, Г1uk, Г1uj Î Г1U, Г2xi Î Г2X.
6. Получаем множество образов F2U1 ребер U1 относительно предиката смежности F2(U1, U1) для чего при i ¹ k:
– копируем F2uj из F2U1, если ребро uk не было смежно ребру uj или было и остается смежным после его удаления из образов вершин Xk²,
– удаляем из образа F2uj ребро uk, если оно становится не смежным ребру uj после его удаления из образов вершин Xk².
Образ F2uk ребра uk получаем как объединение образов Г1xi вершин, инцидентных этому ребру после удаления из его образа Г2uk множества вершин Xk':
F2U1 = {F2uj ∕ uj Î U1}, где при i ¹ k:
ìF2uj : Г2uj Ç Xk² = Æ,
F2uj = í
îF2uj \ uk : uk Î F2uj & Г2uj Ç {Г1uk \ Xk²} = Æ,
здесь: F2uj Î F2U, Г2uj Î Г2U, Г1uk Î Г1U.
F2uk = È Г1xi, где Г1xi Î Г1X, Г2uk Î Г2U.
xi Î Г2uk \ Xk'
7. Получаем множество прообразов F2-1U1 ребер U1 относительно предиката смежности F2(U1, U1) для чего при i ¹ k:
– копируем F2-1uj из F2-1U1, если ребру uk не было смежно ребро uj или было и остается смежным после удаления uk из прообразов вершин Xk',
– удаляем из прообраза F2-1uj ребро uk, если ребро uj становится не смежным ребру uk после его удаления из прообразов вершин множества Xk'.
Прообраз F2-1uk ребра uk получаем как объединение прообразов Г2xi рёбер, которым инцидентна вершина xi после удаления множества вершин Xk²из прообраза Г1uk ребра uk:
F2-1U1 = {F2-1uj ∕ uj Î U1}, где при i ¹ k:
ìF2-1uj : Г1uj Ç Xk' = Æ,
F2-1uj = í
îF2-1uj \ uk : uk Î F2-1uj & Г1uj Ç {Г2uk \ Xk'} = Æ,
здесь: F2-1uj Î F2-1U, Г1uj Î Г1U, Г2uk Î Г2U.
F2-1uk = È Г2xi, где Г2xi Î Г2X, Г1uk Î Г1U.
xi Î Г1uk \ Xk²
Множества аналитического представления куска ультраграфа HU1к получаем по таким же формулам; дополнительно формируем множество внешних рёбер U1кext, в которое включаем ребро uk, и определяем множество внутренних рёбер куска U1кint, исключая из U1к ребро uk:
U1кext = {uk }, U1кint = U1к \ uk.
Формальное описание операции над гиперграфом H (X, U).
При выполнении условия (14) получаем множества гиперграфа H1:
X1 = X; U1 = U;
Г1X1 = {Г1xi : xi Ï Xk' Ú Г1xi \ uk : xi Î Xk' ∕ xi Î X1, Г1xi Î Г1X};
Г2U1 = {Г2uj : j ¹ k Ú Г2uj \ Xk' : j = k ∕ uj Î U1, Г2uj Î Г2U};
F1X1 = { F1xi ∕ xi Î X1}, здесь:
ìF1xi : xi Ï Г2uk,
F1xi = í
î È {Г2uj \ xi : |Г2uj| > 1 Ú Г2uj : |Г2uj| = 1} : xi Î Xk',
uj Î Г1xi \ uk
F1xi Î F1X, Г2uj, Г2uk Î Г2U, Г1xi Î Г1X;
F2U1 = { F1uj ∕ uj Î U1}, здесь для uj ¹ uk
ìF2uj : Г2uj Ç Xk' = Æ,
F2uj = í
î F2uj \ uk : uj Î F2uk & Г2uj Ç {Г2uk \ Xk'} = Æ,
здесь: F2uj Î F2U, Г2uj, Г2uk Î Г2U и
F2uk = È {Г1xi \ uk : | Г2uk| >1 Ú Г1xi : |Г2uk | = 1},
xi Î Г2uk \ X k'
здесь: F2uj Î F2U, Г2uj, Г2uk Î Г2U, Г1xi Î Г1X.
В случае выполнения условия (15) получаем кусок гиперграфа
HU1к (X1к, U1к), в котором множества X1к, U1к, Г1X1к, Г2U1к, F1X1к, F2U1к формируются по тем же правилам, что и множества гиперграфа H1 (X1, U1), а U1кext = {uk}, U1кint = U1к \ uk.
Если результатом операции является несколько компонент связности и определены множества их вершин {Xl}, множество ребер каждой компоненты будет:
Ul = {uj Î È {Г1'xi È Г2'xi} ∕ Г1xi Î Г1X, Г2xi Î Г2X},
xiÎXl
где Г1'xi = Г1xi, если xi Ï Xk² и Г1'xi = Г1xi \ uk, если xi Î Xk², Г1xi Î Г1X,
Г2'xi = Г2xi, если xi Ï Xk' и Г2'xi = Г2xi \ uk, если xi Î Xk', Г2xi Î Г2X.
Остальные множества аналитческого задания компоненты определяются по соответствующим формулам для компоненты данного вида.
Асимптотическая оценка вычислительной сложности данной операции над ультраграфом без учета операций формирования образов и прообразов относительно предикатов смежности равна:
· в худшем – О(n × m) при m > n, если|Г1xi| или|Г2xi| ограничены m либо|Г2uj| или |Г1uj| ограничены n; О(n2) при n > m, если |Г2uj| и |Xk'| либо |Г1uj| и |Xk²| ограничены величинами m и n соответственно;
· в лучшем О(n) при n> m и О(m) при m > n, если|Г1xi|,|Г2xi|,|Г2uj| , |Г1uj|, |Xk'| и |Xk²| ограничены константой.
Асимптотическая оценка вычислительной сложности операции над гиперграфом имеет тот же порядок.
Операция может быть применена к куску ультра- или гиперграфа. Результатом будет кусок HU1к или H1к соответственно. Если ребро uk было внутренним и выполнялось условие (13) для ультраграфа или (15) для гиперграфа, то это ребро исключается из множесва внутренних и добавляется в множество внешних.
Пример. В схеме, показанной на рис. 10, а, отсоединим цепь с1 от эле-ментов э3 и э4. Для модели схемы в виде ультраграфа (смотри рис. 10, б) множества Xk² = {x4}, Xk' = {x3}, т.е. будет выполняться операция удаления ребра u1 из образа вершины x4 и прообраза вершины x3.
Результатом операции HU1 (X1, U1) = HU (X, U) : { Г1Xk², Г2Xk'} \ uk будет ультраграф HU1, так как вершины x3 и x4 не являются расщепляющими и выполняется условие (12). Образы и прообразы вершин и ребер ультраграфа HU1 относительно предикатов инцидентности и смежности будут:
Г1X1: Г1x1 = {u1, u2}, Г1x2 = Г1x3 = Æ, Г1x4 = {u1} \ u1 = Æ;
Г2X1: Г2x1 = Æ, Г2x2 = {u1, u2}, Г2x3 = {u1, u2} \ u1 = {u2}, Г2x4 = {u2};
Г2U1: Г2u1 = {x2, x3} \ {x3} = {x2}, Г2u2 = {x2, x3, x4};
Г1U1: Г1u1 = {x1, x4} \ {x4} = {x1}, Г1u2 = {x1};
F1X1: F1x1 = Г2u2 È Г2u1 \ {x3} = {x2, x3, x4}; F1x2 = F1x3 = Æ, F1x4 = Æ;
F1-1X1: F1-1x1 = Æ, F1-1x2 = Г1u2 È Г1u1 \ {x4} = {x1}, F1-1x3 = Г1u2 = {x1},
F1-1x4 = {x1};
F2U1: F2u1 = Г1x2 = Æ, F2u2 = F2u2 \ u1 = Æ;
F2-1U1: F2-1u1 = Г2x1 = Æ, F2-1u1 = Æ.
В гиперграфе, показанном на рис. 10, в, удалим ребро u1 из образов вершин x3 и x4. Так как |Г2u1 \ {x3, x4}| = 2, в результате выполнения операции H1 (X1, U1) = H (X, U) : {Г1Xk², Г2 Xk'} \ uk получаем гиперграф H1, изображенный на том же рисунке, в котором:
Г1X1: Г1x1 = Г1x2 = {u1, u2}, Г1x3 = Г1x4 = {u1, u2} \ u1 = {u2};
Г2U1: Г2u1 = {x1, x2, x3, x4} \ {x3, x4} = {x1, x2}, Г2u2 = {x1, x2, x3, x4};
F1X1: F1x1 = {x2, x3, x4}, F1x2 ={x1, x3, x4}, F1x3 ={x1, x1, x4},
F1x4 = {x1, x2, x3};
F2U1: F2u1 = {u2}, F2u2 = {u1}.
При удалении ребра u1 из образов вершин x2, x3, x4 получим кусок ультра- HU1к или гиперграфа H1к, аналитическое представление которых читателю нетрудно получить самостоятельно.
Формирование части ультраграфа HU или гиперграфа H – рис. 11. Реализует проектную операцию определения (локализации) части схемы по заданному множеству элементов Э1 É Э, где Э – множество элементов схемы.

Рисунок 11 – Схема и выделенный фрагмент (а); модель в виде ультраграфа HU, сформированные кусок HU1к – две компоненты связности и подграф HU1 – три компоненты связности (б); модель в виде гиперграфа, кусок и подграф гиперграфа H1к и H1 – две и три компоненты связности соответственно (в)
Операция имеет две модификации: формирование куска HU1к ультраграфа HU или H1к гиперграфа H и формирование подграфа HU1 ультраграфа или подграфа H1 гиперграфа.
Задается множество X1 вершин формируемой части графа.
Обозначение операции: HU (X, U) ¤ X1 или H (X, U) ¤ X1 для формирования куска ультра- или гиперграфа и HU (X,U) ○ X1 или H (X, U) ○ X1 для формирования подграфов тех же графов.
Условие корректности операции: X1 Ì X.
Результатом выполнения операции является:
– кусок ультраграфа HU1к (X1к, U1к) = HU (X, U) ¤ X1или
– гиперграфа H1к (X1к, U1к) = H (X, U) ¤ X1 либо
– подграф ультраграфа HU1 (X1, U1) = HU (X, U) ○ X1 или
– подграф гиперграфа H1 (X1, U1) = H (X, U) ○ X1.
Полученная часть ультра- или гиперграфа может содержать несколько компонент связности. Операция не формирует аналитическое представление каждой компоненты связности. Множества вершин, ребер, образов и прообразов (для ультраграфа) формируемой части графа представляют собой конкатенацию соответствующих множеств компонент связности, входящих в эту компоненту.
Содержательно-формальное описание выполнения операции при
получении куска HU1к (X1к, U1к) ультраграфа HU (X, U).
1. Копируем множество X1 под наименованием X1к : X1к = X1.
2. Формируем множество U1к, включая в него при копировании те рёбра множества U, которые инцидентны вершинам множества X1 и которым инцидентны эти вершины:
U1к = Г1(X1к) È Г2(X1к), где Г1(X1к) = È Г1xi, Г2(X1к)= È Г2xi,
xi Î X1к xi Î X1к
где Г1xi Î Г1X, Г2xi Î Г2X, Г1(X1к) – множество ребер, которые инцидентны вершинам множества X1, Г2(X1к) – множество ребер, которым инцидентны эти вершины.
Примечание: множество U1к можно определить другим способом, а именно:
U1к = {uj Î U : {Г2uj È Г1uj} Ç X1к ¹ Æ / Г2uj Î Г2U, Г1uj Î Г1U}.
Однако использование этой формулы в данном случае нецелесообразно, так как это приведет к тому, что вычислительная сложность операции «в лучшем» будет О(m) даже при |Г2uj| = |Г1uj| = |X1к | = const. Аналогичная формула будет использована для определения U1 подграфа ультраграфа. Читателю предлагается самому продумать основания для её применения.
3. Определяем множество U1кint внутренних ребер, включая в него те ребра из U1к, у которых все вершины их образов и прообразов принадлежат множеству вершин X1к:
U1кint = {uj Î U1к : {Г2uj È Г1uj} Í X1к / Г2uj Î Г2U, Г1uj Î Г1U}.
4. Создаем множество U1кext внешних ребер, исключая из множества U1к внутренние ребра куска ультраграфа:
U1кext = U1к \ U1кint.
5. Получаем множество Г1X1к образов вершин куска HU1к, записывая в него из Г1X образы xi Î X1к:
Г1X1к = {Г1xi Î Г1X / xi Î X1к }.
6. Формируем множество Г2X1к прообразов вершин куска HU1к, записывая в него из Г2X прообразы xi Î X1к:
Г2X1к = {Г2xi Î Г2X / xi Î X1к }.
7. Создаем множество Г2U1к образов ребер куска HU1к так, что образом внутреннего ребра является образ Г2uj одноименного ребра в Г2U ультраграфа HU, а образ внешнего ребра определяется как Г2uj Ç X1к, т. е. удалением вершин, не принадлежащих X1к:
Г2U1к = {Г2uj Ç X1к / uj Î U1к, Г2uj Î Г2U}.
8. Создаем множество Г1U1к прообразов ребер куска HU1к так, что прообразом внутреннего ребра является прообраз Г1uj одноименного ребра в Г1U ультраграфа HU, а прообраз внешнего ребра определяется как Г1uj Ç X1к, т. е. удалением вершин, не принадлежащих X1к:
Г1U1к = {Г1uj Ç X1к / uj Î U1к, Г1uj Î Г1U}.
9. Определяем множество F1X1к образов и прообразов F1-1X1к вершин относительно предиката смежности F1(X1к, X1к), оставляя в F1xi Î F1X и F1-1xi Î F1-1X только те вершины, которые принадлежат множеству X1к:
F1X1к = {F1xi Ç X1к / xi Î X1к, F1xi Î F1X},
F1-1X1к = {F1-1xi Ç X1к / xi Î X1к, F1-1xi Î F1-1X}.
10. Формируем множество F2U1к образов и прообразов F2-1U1к рёбер относительно предиката смежности F2(U1к, U1к), оставляя в F2uj Î F2U и F2-1uj Î F2-1U только те ребра, которые принадлежат множеству U1к:
F2U1к = { F2uj Ç U1к / uj Î U1к, F1uj Î F2U },
F2-1U1к = { F2-1uj Ç U1к / uj Î U1к, F2-1 uj Î F2-1U }.
Для данной операции целесообразно подробно рассмотреть определение количества операций формирования множества ребер куска ультраграфа U1к.
Формирование множества U1к подразумевает:
– определение множества ребер Г1(X1к), которые инцидентны вершинам множества X1, и множества ребер Г2(X1к), которым инцидентны эти вершины. В предположении, что все ребра в Ui = Г1xi для всех xi Î X1к различны, реализация выражений
È Г1xi и È Г2xi
xi Î X1к xi Î X1к
потребует (|Г1xi|2 + |Г2xi|2) ´ St операций , где t = 1, |X1к|;
– определение множества ребер U1к = Г1(X1к) È Г2(X1к), что потребует |Г1(X1к)| ´ |Г2(X1к)| операций сравнения.
Мощности получаемых множеств будут:
– |Г1(X1к)| и |Г2(X1к)| ограничены m или константой, если |Г1xi| и |Г2xi| ограничены теми же величинами;
– |U1к| – ограничена m или константой, если |Г1(X1к)| и |Г2(X1к)| ограничены теми же величинами.
Таким образом асимптотическая оценка сложности формирования множества U1к в худшем будет О(m2×n2), если |Г1xi|, |Г2xi| ограничены m и |X1к| ограничена n, и в лучшем О(1), если они ограничены константой.
Асимптотическая оценка вычислительной сложности данной операции при формировании куска ультраграфа равна:
· в худшем О(n2×m2), если |Г1xi|, |Г2xi| ограничены m и |X1к| ограничена n;
· в лучшем О(m×n), если |Г2uj| = const, а |U1к| и |X1к| ограничены m и n соответственно или О(1), если |X1к|, |U1кext| и |Г2uj| ограничены константой.
Формальное описание выполнения операции получения подграфа HU1 (X1, U1) ультраграфа HU (X, U):
U1 = {uj Î U : {Г2uj È Г1uj} Í X1 / Г2uj Î Г2U, Г1uj Î Г1U}(в отличие от куска ультраграфа у подграфа в множество U1 входят только внутренние ребра);
Г1X1 = {Г1xi Ç U1 / xi Î X1, Г1xi Î Г1X};
Г2X1 = {Г2xi Ç U1 / xi Î X1, Г2xi Î Г2X};
Г2U1 = {Г2uj Î Г2U / uj Î U1};
Г1U1 = {Г1uj Î Г1U / uj Î U1};
F1X1 = {F1xi : F1xi Í X1 Ú È Г2uj : F1xi Ë X1 / xi Î X1, F1xi Î F1X,
uj Î Г1xi Ç U1
Г2uj Î Г2U, Г1xi Î Г1X };
F1-1X1 = {F1-1xi : F1-1xi Í X1 Ú È Г1uj : F1-1xi Ë X1 / xi Î X1, F1-1xi Î F1-1X,
uj Î Г2xi Ç U1
Г1uj ÎГ1U, Г2xi Î Г2X };
F2U1 = {F2uj Ç U1 / uj Î U1, F1uj Î F2U};
F2-1U1 = {F2-1uj Ç U1 / uj Î U1, F2-1uj Î F2-1U}.
Формальное описание выполнения операции получения куска
H1к (X1к, U1к) гиперграфа H (X, U).
X1к = X1; U1к = Г1(X1к), где Г1(X1к) = È Г1xi, Г1xi Î Г1X;
xiÎX1к
U1кint = {uj Î U1к : Г2uj Í X1к / Г2uj Î Г2U}, U1кext = U1к \ U1кint;
Г1X1к = {Г1xi Î Г1X / xi Î X1к};
Г2U1к = {Г2uj : uj Î U1кint Ú Г2uj Ç X1к : uj Î U1кext / uj Î U1к, Г2uj Î Г2U};
F1X1к = {F1xi Ç X1к / xi Î X1к, F1xi Î F1X};
F2U1к = {F2uj Ç U1к / uj Î U1к, F1uj Î F2U}.
Формальное описание выполнения операции получения подграфа H1 (X1, U1) гиперграфа H (X, U):
U1 = {uj Î U : Г2uj Í X1 / Г2uj Î Г2U};
Г1X1 = {U1i Ç U1 / xi Î X1, U1i = Г1xi Î Г1X};
Г2U1 = {Г2uj Î Г2U / uj Î U1};
F1X1 = {F1xi / xi Î X1}, где
ìF1xi : F1xi Í X1, здесь и далее F1xi Î F1X,
F1xi = í È Xi : F1xi Ë X1, где Xi = Г2uj \ xi : |Г2uj | >1 Ú Г2uj : | Г2uj| = 1,
îuj Î Г1xi Ç U1
Г1xi Î Г1X, Г2uj Î Г2U;
F2U1 = { F2uj Ç U1 / uj Î U1, F1uj Î F2U}.
Вычислительная сложность операции над гиперграфом имеет тот же порядок, что и для ультраграфа.
Операция может быть применена для выделения части из куска ультра- или гиперграфа. В этом случае при определении множества внутренних ребер U1кint необходимо дополнительно проверять не было ли ребро внешним в куске HUк. Тогда при выполнении операции, например над куском ультраграфа, выражение в п.п. 3 должно иметь вид:
U1кint = {uj Î U1к & uj Ï Uкext : {Г2uj È Г1uj} Í X1к / Г2uj Î Г2U,
Г1uj Î Г1U}.
Пример. В схеме, показанной на рис. 11, а, выделим фрагмент, включающий элементы э1, э2, э3, э4, э5. Тогда множество вершин формируемого куска ультраграфа HU1к – X1к = X1 = {x1, x2, x3, x4, x5}. Остальные множества аналитического представления этого куска в результате выполнения операции HU1к (X1к,U1к) = HU (X,U) ¤ X1 будут:
U1к = Г1(X1) È Г2(X1) = {u4, u3, u1 } È {u4, u1} = { u4, u3, u1}, U1кint = {u4}, так как только для ребра u4 справедливо условие Г2u4 È Г1u4 = { x2, x5, x1} Í X1, и U1кext = {u3, u1 };
Г1X1к = {Г1xi Î Г1X / xi Î X1} = {{u4}, {u3}, Æ, {u1}, Æ};
Г2X1к = {Г2xi Î Г2X / xi Î X1} = {Æ, {u4}, {u1}, Æ, {u4}};
Г2U1к : Г2u4 = {x2, x5}, Г2u3 = {x10, x11} Ç X1к = Æ,
Г2u1 = {x3, x6} Ç X1к = {x3};
Г1U1к : Г1u4 = {x1}, Г1u3 = {x2} Ç X1к = {x2}, Г1u1 = {x4} Ç X1к ={x4};
F1X1к : F1x1 = {x2, x5} Ç X1к = {x2, x5}, F1x2 = {x10, x11} Ç X1к = Æ, F1x3 = Æ, F1x4 = {x3, x6} Ç X1к = {x3}, F1x5 = Æ;
F1-1X1к : F1-1x1 = Æ, F1-1x2 = {x1} Ç X1к = {x1}, F1-1x3 = {x4} Ç X1к = {x4},
F1-1x4 = Æ, F1-1x5 = {x1} Ç X1к = {x1};
F2U1к : F2u4 = {u3} Ç U1к = {u3}, F2u3 = Æ, F2u1 = {u2} Ç U1к =Æ;
F2-1U1к : F2-1u4 =Æ, F2-1u3 = {u4} Ç U1к = {u4}, F2-1u1 = Æ.
Для подграфа ультраграфа при том же X1 получим:
U1 = {u4};
Г1X1 = {{u4}, Æ, Æ, Æ, Æ}; Г2X1 = {Æ, {u4}, Æ, Æ, {u4}};
Г2U1 : Г2u4 = {x2, x5}; Г1U1 : Г1u4 = {x1};
F1X1 : F1x1 = {x2, x5}, F1x2 = F1x3 = F1x4 = F1x5 = Æ;
F1-1X1 : F1-1x1 = Æ, F1-1x2 = {x1} , F1-1x3 = Æ, F1-1x4 = Æ, F1-1x5 = {x1};
F2U1 : F2u4 = {u3} Ç U1 = Æ; F2-1U1к : F2-1u4 = Æ.
При использовании в качестве модели схемы гиперграфа множества аналитического представления куска H1к (X1к, U1к, Г1X1к, Г2U1к) будут:
X1 = {x1, x2, x3, x4, x5};
U1к = Г1(X1) = {u4, u3, u1}, U1кint = {u4}, U1кext = {u3, u1};
Г1X1к = {Г1xi Î Г1X / xi Î X1} = {{u4}, {u3,u4}, {u1}, {u1}, u4}};
Г2U1к : Г2u4 = {x1, x2, x5}, Г2u3 = {x2, x10, x11} Ç X1к = {x2},
Г2u1 = {x3, x4, x6} Ç X1 = {x3, x4};
Окончание статьи будет опубликовано в последующих выпусках.
Литература
1. Овчинников В.А. Математические модели объектов задач структурного синтеза: Наука и образование. Инженерное образование: Эл. науч. издание. – 2009. – ╧ 4.
Публикации с ключевыми словами: структурный синтез, математические модели
Публикации со словами: структурный синтез, математические модели
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



