научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2009
УДК 004
УДК 004.3 +519.6
(окончание, начало смотри «Наука и образование.
Инженерное образование: Эл. науч. издание. – 2009 – ╧ 10, 11чание»)
В заключительной части статьи рассмотрены операции свертки множества вершин графов, декомпозиции вершины, т. е. замены её частью графа, дополнения части до графа или его куска, объединения и пересечения графов. Эти операции необходимы для организации процесса проектирования при блочно-иерархическом подходе:
– для получения описания объекта при замене его фрагментов компонентами более высокого уровня иерархии;
– для реализации методов последовательной детализации и выделения частей объекта;
– для объединения фрагментов структуры объекта;
– для выполнения процедур контроля.
Все сказанное является общими замечаниями и не ограничивает возможности применения этих операций.
Свертка (факторизация) множества Xсв вершин ультраграфа HU или гиперграфа H – рис. 12. Соответствует проектной операции замены части схемы макроэлементом.

Рисунок 12 – Фрагмент схемы (а), ее модель в виде ультраграфа HU и результат операции ультраграф HU1 и кусок ультраграфа HUсвк (б), гиперграф H(X, U) и результат операции гиперграф H1 и кусок Hсвк (в)
Задается множество сворачиваемых вершин Xсв.
Обозначение операции: HU (X, U ∕ Xсв ~ xсв) и H (X, U ∕ Xсв ~ xсв для ультра- и гиперграфа соответственно.
Условие корректности операции: Xсв Í X.
В результате выполнения операции для случая Xсв Ì X получаем:
– ультраграф HU1 (X1, U1) = HU (X, U ∕ Xсв ~ xсв) или
– гиперграф H1 (X1, U1) = H (X,U ∕ Xсв ~ xсв).
В качестве моделей схем соединения элементов, составляющих макроэлемент, формируются также куски ультраграфа HUсвк (Xсвк, Uсвк) или гиперграфа Hсвк (Xсвк, Uсвк).
Для варианта Xсв = X операцию обозначим как factor (HU (X, U)) для ультра- и factor (H (X, U)) гиперграфа соответственно. Результат операции:
– для ультраграфа HU (X, U) это тривиальный ультраграф
HUF (xсв, Æ) = factor (HU (X, U));
– для гиперграфа H (X, U) это тривиальный гиперграф
HF (xсв, Æ) = factor (H (X, U));
– для куска ультраграфа HUк (Xк, Uк) это одновершинный кусок
HUFк (xсв, Uкext) = factor (HUк (Xк, Uк)), где Uкext – множество внешних ребер преобразуемого куска HUк;
– для куска гиперграфа Hк (Xк, Uк) это одновершинный кусок
HFк (xсв, Uкext) = factor (Hк (Xк, Uк)), где Uкext – множество внешних ребер преобразуемого куска Hк.
Для всех случаев моделью макроэлемента HUсв или HUсвк и Hсв или Hсвк будет сам исходный граф или кусок HU (X, U) или HUк (Xк, Uк) и H (X, U) или Hк (Xк, Uк).
Содержательно–формальное описание результата операции в виде ультраграфа HU1 (X1, U1).
1. Формируем множество X1, исключая из X вершины множества Xсв и добавляя вершину xсв:
X1 = (X \ Xсв) · xсв, где xсв ~ Xсв.
2. Создаем множество рёбер Uсв, включая в него ребра ujÎU, если множество вершин инцидентных ребру и множество вершин, которым оно инцидентно, принадлежит только множеству Xсв:
Uсв = {uj Î U* : {Г2uj È Г1uj} Í Xсв / Г2uj Î Г2U, Г1uj Î Г1U},
где: U* = {Г1Xсв È Г2Xсв}, Г1Xсв = È Г1xi, Г2Xсв = È Г2xi.
xi Î Xсв xi Î Xсв
Примечание: множество Uсв является множеством внутренних ребер Uсвк куска ультраграфа HUсвк.
3. Получаем множество U1, удаляя из множества U множество Uсв:
U1 = U \ Uсв.
4. Формируем множество образов Г1X1, исключая из множества Г1X образы вершин множества Xсв. После чего в множество Г1X1 добавляем образ свернутой вершины xсв. В образ Г1xсв входят ребра множества U1, инцидентные вершинам множества Xсв:
Г1X1 = Г1X \ {Г1xi / xi Î Xсв, Г1xi Î Г1X } · Г1xсв,
где Г1xсв = È Г1xi \ Uсв, Г1xi Î Г1X
xi Î Xсв
или Г1xсв = {uj : Г1uj Ç Xсв ¹ Æ/ uj Î U1, Г1uj Î Г1U}.
5. Создаем множество прообразов Г2X1, исключая из множества Г2X прообразы вершин множества Xсв. После чего в множество Г2X1 добавляем прообраз свернутой вершины xсв. В Г2xсв входят ребра множества U1, которым инцидентны вершины множества Xсв
Г2X1 = Г2X \ {Г2xi / xi Î Xсв, Г2xi Î Г2X } · Г2xсв,
где Г2xсв = È Г2xi \ Uсв, Г2xi Î Г2X
xi Î Xсв
или Г2xсв = {uj : Г2uj Ç Xсв ¹ Æ / uj Î U1, Г2uj Î Г2U}.
6. Получаем множество образов Г2U1, копируя из Г2U образы Г2uj рёбер uj Î U1 и удаляя при этом из образов рёбер, которым инцидентны вершины множества Xсв, вершины, принадлежащие этому множеству, и добавляя вершину xсв:
Г2U1 = {Г2uj / uj Î U1}, где
ìГ2uj Î Г2U : Г2uj Ç Xсв = Æ,
Г2uj = í
î{Г2uj \ Xсв} · xсв : Г2uj Ç Xсв ¹ Æ.
7. Формируем множество прообразов Г1U1, копируя из Г1U прообразы Г1uj рёбер uj Î U1 и удаляя при этом из прообразов рёбер, инцидентных вершинам множества Xсв, вершины, которые принадлежат этому множеству, и добавляя вершину xсв:
Г1U1 = {Г1uj / uj Î U1}, где
ìГ1uj Î Г1U : Г1uj Ç Xсв = Æ,
Г1uj = í
î{Г1uj \ Xсв} · xсв : Г1uj Ç Xсв ¹ Æ.
8. Определяем множество F1X1 образов вершин относительно предиката смежности F1(X, X). Для чего:
– копируем F1xi из F1X, если вершине xi не инцидентна ни одна из вершин множества Xсв,
–удаляем вершины множества Xсв из образа F1xi Î F1X и добавляем в него вершину xсв в противном случае:
F1X1 = { F1xi / xi Î X 1}, здесь для xi ¹ xсв
ìF1xi : F1xi Ç Xсв = Æ,
F1xi = í
î(F1xi \ Xсв) · xсв : F1xi Ç Xсв ¹ Æ,
F1xсв = È F1xi \ Xсв, где F1xi Î F1X.
xi Î Xсв
Вершины, смежные свернутой, получаем объединяя образы вершин множества Xсв и удаляя из результата вершины множества Xсв.
9. Получаем множество F1-1X1 прообразов вершин. Для чего:
– копируем F1-1xi из F1-1X, если вершина xi не инцидентна ни одной из вершин множества Xсв,
– удаляем вершины множества Xсв из прообраза F1-1xi Î F1-1X и добавляем в него вершину xсв в противном случае:
F1-1X1 = {F1-1xi / xi Î X1}, здесь для xi ¹ xсв
ìF1-1xi : F1- 1xi Ç Xсв = Æ,
F1-1xi = í
î(F1-1xi \ Xсв) · xсв : F1-1xi Ç Xсв ¹ Æ,
F1-1xсв = È F1-1xi \ Xсв , где F1-1xi Î F1-1X.
xi Î Xсв
Прообраз вершины xсв получаем, объединяя прообразы вершин множества Xсв и удаляя из результата вершины множества Xсв.
10. Формируем множество F2U1 образов рёбер, копируя F2uj из F2U, если ребру не инцидентна ни одна из сворачиваемых вершин, и удаляя из него свернутые рёбра в противном случае:
F2U1 = {F2uj / uj Î U1}, здесь
ìF2uj Î F2U : Г2uj Ç Xсв = Æ,
F2uj = í
î{F2uj È Uj¢} \ Uсв : Г2uj Ç Xсв ¹ Æ, где F2uj Î F2U, Г2uj Î Г2U,
Uj¢= È Г1xi \ uj, Г1xi Î Г1X.
xi Î Xсв
11. Получаем множество F2-1U1 прообразов ребер, копируя F2-1uj из
F2-1U, если ребро не инцидентно ни одной из сворачиваемых вершин, и удаляя из него свернутые ребра в противном случае:
F2-1U1 = {F2-1uj / uj Î U1}, где
ìF2-1uj Î F2-1U : Г1uj Ç Xсв = Æ,
F2-1uj = í
î{F2-1uj È Uj¢} \ Uсв : Г1uj Ç Xсв ¹ Æ, где F2-1uj Î F2-1U, Г1uj Î Г1U,
Uj¢ = È Г2xi \ uj, Г2xi Î Г2X.
xi Î Xсв
Формальное описание операции над гиперграфом H1 (X1, U1).
Множества результата операции – гиперграфа H1 (X1, U1) будут:
X1 = (X \ Xсв) · xсв, где xсв ~ Xсв;
U1 = U \ Uсв, где Uсв = {uj Î U : Г2uj Í Xсв / Г2uj Î Г2U};
Г1X1 = Г1X \ {Г1xi /xi Î Xсв, Г1xi Î Г1X} · Г1xсв, где Г1xсв = È Г1xi \ Uсв,
xi Î Xсв
или Г1xсв = {uj : Г2uj Ç Xсв ¹ Æ / uj Î U1, Г2uj Î Г2U};
Г2U1 = {Г2uj / uj Î U1}, где
ìГ2uj, если Г2uj Ç Xсв = Æ и Г2uj Î Г2U,
Г2uj = í
î(Г2uj \ Xсв) · xсв, если Г2uj Ç Xсв ¹ Æ;
F1X1 = { F1xi / xi Î X1}, здесь для xi ¹ xсв
ìF1xi : F1xi Ç Xсв = Æ,
F1xi = í
î(F1xi \ Xсв) · xсв : F1xi Ç Xсв ¹ Æ,
F1xсв = È F1xi \ Xсв, где F1xi Î F1X;
xi Î Xсв
F2U1 = {F2uj / uj Î U1}, здесь
ìF2uj Î F2U : Г2uj Ç Xсв = Æ,
F2uj = í
î{F2uj È Uj¢}\ Uсв : Г2uj Ç Xсв ¹ Æ, где F2uj Î F2U, Г2uj Î Г2U,
Uj¢ = È Г1xi \ uj, Г1xi Î Г1X.
xi Î Xсв
Куски ультраграфа HUсвк (Xсвк, Uсвк) и гиперграфа Hсвк (Xсвк, Uсвк) определяются так же, как HU1к (X1к, U1к) и H1к (X1к, U1к) в операции «формирование части ультраграфа HU или гиперграфа H» [2].
Асимптотическая оценка вычислительной сложности данной операции без учета операций определения образов и прообразов вершин и ребер относительно предикатов смежности равна:
· в худшем О(n2×m), если |Г2uj|, |Г1uj| и |Xсв| ограничены n;
· в лучшем О(n) при n > m и О(m) при m > n, если |Г2uj|, |Г1uj|,|Г1xi|,
|Г2xi| и |Xсв| ограничены константой.
Операция применима также к кускам ультра- и гиперграфа, при этом HU1 и H1 будут кусками ультра- и гиперграфа соответственно. Множества внешних ребер этих кусков равны множествам внешних ребер исходных графов.
Пример. Объединим в макроэлемент элементы э2 и э3 схемы, показанной на рис. 12, а. В результате операции HU1 (X1, U1) = H (X, U ∕ Xсв Þ xсв) свертки вершин множества Xсв = {x2, x3} ультраграфа HU получим ультраграф HU1 и кусок ультраграфа HUсвк (смотри рис. 12, б). Множества аналитического представления ультраграфа HU1 (X1, U1) будут:
X1 = {x1, x4, x5, . . . , x10, xсв};
Uсв = {u4}, так как Г2u4 È Г1u4 = {x2} È {x3} = {x2, x3} = Xсв,
U1 = U \ Uсв = {u1, u2, u3, u5};
Г1X1 = {Г1x1, Г1x4, Г1x5, . . . , Г1x10} · Г1xсв, где Г1xсв = {{Г1x2 È Г1x3} \ u4} = {{u2, u3, u4} \ u4} = {u2, u3};
Г2X1 = {Г2x1, Г2x4, Г2x5, . . . , Г2x10} · Г2xсв, где Г2xсв = {u1, u2};
Г2U1: Г2u1 = {{x2, x4} \ {x2, x3} · xсв } = {x4, xсв}, Г2u2 = {{x3, x5, x6} \ {x2, x3} · xсв} = {x5, x6, xсв}, Г2u3 = {x7, x8}, Г2u5 = {x9, x10};
Г1U1: Г1u1 = {x1}, Г1u2 = {{x2} \ {x2, x3} · xсв = {xсв}, Г1u3 = {x3} \ {x2, x3} · xсв}= {xсв}, Г1u5 = {x4};
F1X1: F1x1 = {{x2, x4} \ {x2, x3} · xсв} = {x4, xсв}, F1x4 ={x9, x10}, F1x5 = F1x6 = F1x7 = F1x8 = F1x9 = F1x10 = Æ, F1xсв = {{x5, x6, x3} È {x2, x7, x8} \ {x2, x3}} = {x5, x6, x7, x8};
F1-1X1: F1-1x1 = Æ, F1-1x4 = {x1}, F1-1x5 = F1-1x6 = {{x2} \ {x2, x3} · xсв } = {xсв}, F1-1x7 = F1-1x8 = {{x3} \ {x2, x3} · xсв } = {xсв}, F1-1x9 = F1-1x10 = {x4},
F1-1xсв = {{x1, x3} È {x2} \ {x2, x3}}= {x1};
F2U1: F2u1 = {{u2, u5} È {{ u2}\{u1} È {u3, u4} \ {u1}} \ u4} = {u2, u3, u5}, F2u2 = {{u3, u4} È {{ u2} \ {u2} È { u3, u4} \ {u2}} \ u4} = {u3}, F2u3 = F2u5 = Æ;
F2-1U1: F2-1u1 = Æ, F2-1u2 = {{u1, u4} È {{u1, u4} \ {u2} È {u2} \ {u2}} \ u4} = {u1} , F2-1u3 = {{u2} È {{u1, u4} \ {u3} È {u2} \ {u3}}\ u4}} = {u2, u1},
F2-1u5 ={u1}.
Кусок ультраграфа HUсвк (Xсвк, Uсвк) получим по формулам для куска ультраграфа HU1к в операции «формирование части ультраграфа HU или гиперграфа H» [2]. В этих формулах множество X1к следует заменить на Xсвк, а множество U1к – на множество Uсвк:
Xсвк = {x2, x3},
Uсвк = Г1(Xсвк) È Г2(Xсвк), Uсвк = {u2, u3, u4, u1},
Uсвкint = {uj Î Uсвк : {Г2uj È Г1uj} Í Xсвк / Г2uj Î Г2U, Г1uj Î Г1U},
Uсвкint = {u4},
Uсвкext = Uсвк \ Uсвкint, Uсвкext = {u2, u3, u1};
Г1Xсвк = {Г1xi Î Г1X / xi Î Xсвк}, Г1Xсвк = {Г1x2, Г1x3} = {{u2}, {u3,u4}};
Г2Xсвк = {Г2xi Î Г2X / xi Î Xсвк}, Г2Xсвк = {Г2x2, Г2x3} = {{u1, u4}, {u2}};
Г2Uсвк ={Г2uj : uj Î Uсвкint Ú Г2uj Ç Xсвк : uj Î Uсвкext / uj Î Uсвк, Г2uj Î Г2U};
Г2Uсвк : Г2u2 = {x3, x5, x6} Ç {x2, x3} = {x3} , Г2u3 = {x7, x8} Ç {x2, x3} = Æ, Г2u4 = {x2}, Г2u1 = {x2, x4} Ç {x2, x3} = {x2};
Г1Uсвк ={Г1uj : uj Î Uсвкint Ú Г1uj Ç Xсвк : uj Î Uсвкext / uj Î Uсвк, Г1uj Î Г1U};
Г1Uсвк : Г1u2 = {x2} Ç {x2, x3} = {x2}, Г1u3 = {x3} Ç {x2, x3} = {x3},
Г1u4 = {x3}, Г1u1 = {x1} Ç {x2, x3} = Æ;
F1Xсвк = {F1xi Ç Xсвк / xi Î Xсвк, F1xi Î F1X };
F1Xсвк : F1x2 = {x3, x5, x6} Ç {x2, x3} = {x3}, F1x3 = {x2, x7, x8} Ç {x2, x3} = {x2};
F1-1Xсвк = {F1-1xi Ç Xсвк / xi Î Xсвк, F-1xi Î F1-1X };
F1-1Xсвк : F1-1x2 = {x1, x3} Ç {x2, x3} = {x3}, F1-1x3 = {x2} Ç {x2, x3} = {x2};
F2Uсвк = {F2uj Ç Uсвк / uj Î Uсвк, F2uj Î F2U };
F2Uсвк: F2u2 = {u3, u4} Ç {u2, u3, u4, u1} = {u3, u4}, F2u3 = Æ , F2u4 = {u2} Ç {u2, u3, u4, u1} = {u2}, F2u1 = {u2, u5} Ç {u2, u3, u4, u1} = {u2};
F2-1Uсвк = {F2-1uj Ç Uсвк / uj Î Uсвк, F2-1uj Î F2-1U };
F2-1Uсвк: F2-1u2 = {u1, u4} Ç {u2, u3, u4, u1} = {u1, u4}, F2-1u3 = { u2} Ç {u2, u3, u4, u1} = {u2}, F2-1u4 = {u2} Ç {u2, u3, u4, u1} = {u2}, F2-1u1 = Æ.
При использовании в качестве модели схемы гиперграфа H результатом операции H1 (X1, U1, Г1X1, Г2U1) = H (X, U, Г1X, Г2U ∕ Xсв Þ xсв) будет гиперграф H1 и кусок гиперграфа Hсвк.
Гиперграф H1 (X1, U1, Г1X1, Г2U1):
X1 = {x1, x4, x5, . . . , x10, xсв};
Uсв = {u4}, так как Г2u4 = Xсв, U1 = {u1, u2, u3, u5};
Г1X1: Г1x1 = {u1}, Г1x4 = {u1, u5}, Г1x5 = Г1x6 = {u2}, Г1x7 = Г1x8 = {u3};
Г1x9 = Г1x10 = {u5}, Г1xсв = {u1, u2, u3};
Г2U1: Г2u1 = {x1, x4, xсв}, Г2u2 = {x5, x6, xсв},
Г2u3 = {x7, x8, xсв}, Г2u5 = {x4, x9, x10}.
Для куска гиперграфа Hсвк (Xсвк, Uсвк, Г1Xсвк, Г2Uсвк) множества его аналитического представления будут:
Xсвк = Xсв = {x2, x3};
Uсвк = {u2, u3, u4, u1}, Uсвкint = {u4}, Uсвкext = { u2, u3, u1};
Г1Xсвк = {Г1x2, Г1x3}, где Г1x2 = {u1, u2, u4}, Г1x3 = { u2, u3, u4};
Г2Uсвк = {Г2u1, Г2u2, Г2u3, Г2u4}, где Г2u1 = {x2}, Г2u2 = Г2u4 = {x2, x3},
Г2u3 = {x3}.
Декомпозиция вершины xсв ультраграфа HU1 или гиперграфа H1 – рис. 13 . Реализует проектную операцию замены в схеме макроэлемента его схемой на элементах более высокой степени детализации.

Рисунок 13 – Одновершинные куски ультраграфа HUк (xсв, Uк) (а) и гиперграфа
Hк (xсв, Uк) (б)
Выполняется замена одновершинного куска HUк (xсв, Uк) – рис. 13, а ультраграфа HU1 (X1, U1) или одновершинного куска – рис. 13, б гиперграфа H1 (X1, U1) на многовершинный кусок HUсвк (Xсвк, Uсвк) или Hсвк (Xсвк, Uсвк) соответственно. Ультраграф HU1 и многовершинный кусок HUсвк, гиперграф H1 и многовершинный кусок Hсвк показаны на рис. 12, б и в соответственно.
Имеются аналитические представления ультраграфа HU1 или гиперграфа H1 и многовершинных кусков HUсвк или Hсвк соответственно. Куски HUсвк или Hсвк могут быть получены в результате выполнения операции свертки множества вершин либо каким-то другим способом.
Обозначение операции: HU1 (X1, U1 ∕ xсв Þ Xсвк) для ультраграфа и
H1 (X1, U1 ∕ xсв Þ Xсвк) для гиперграфа.
Условия корректности операции: Uк = {Г1xсв È Г2xсв } Í Uсвк для ультраграфа и Uк = Г1xсв Í Uсвк для гиперграфа, Uк = Uсвкext.
В результате выполнения операции формируется: ультраграф
HU (X, U) = HU1 (X1, U1 ∕ xсв Þ Xсвк) или гиперграф
H(X, U) = H1 (X1, U1 ∕ xсв Þ Xсвк).
Содержательно–формальное описание операции получения ультраграфа HU (X, U).
1. Определяем множество X, исключая из X1 вершину xсв и добавляя вершины множества Xсв:
X = (X1 \ xсв) · Xсвк.
2. Формируем множество рёбер U, добавляя в множество U1 множество внутренних ребер Uсвкint куска ультраграфа HUсвк:
U = U1 · Uсвкint.
3. Получаем множества образов Г1X и прообразов Г2X вершин, удаляя из множеств Г1X1 и Г2X1 образ и прообраз вершины xсв и добавляя образы и прообразы вершин множества Xсв многовершинного куска HUсвк (Xсвк, Uсвк):
Г1X = Г1X1 \ Г1xсв · Г1Xсвк, Г1xсв Î Г1X1,
Г2X = Г2X1 \ Г2xсв · Г2Xсвк , Г2xсв Î Г2X1.
4. Формируем множество образов рёбер Г2U, занося в него:
– образ ребра uj из Г2U1, если вершина xсв не инцидентна ему;
– образ ребра uj из Г2U1, удаляя из него вершину xсв и добавляя в него образ ребра из Г2Uсвк, если uj является внешним ребром куска HUсвк;
– образ ребра uj из Г2Uсвкint, если это ребро внутреннее в куске HUсвк:
Г2U = {Г2uj / uj Î U}, где
ìГ2uj Î Г2U1 : xсв Ï Г2uj,
Г2uj = íГ2uj \ xсв · Xj+ : uj Î Uсвкext, где Г2uj Î Г2U1, Xj+ = Г2uj Î Г2Uсвк,
îГ2uj Î Г2Uсвк : uj Î Uсвкint.
5. Создаем множество прообразов рёбер Г1U, занося в него:
– прообраз ребра uj из Г1U1, если оно не инцидентно вершине xсв;
– прообраз ребра uj из Г1U1, удаляя из него вершину xсв и добавляя в него прообраз ребра из Г1Uсвк, если uj является внешним ребром куска HUсвк;
– прообраз ребра uj из Г1Uсвк, если это ребро внутреннее в куске HUсвк:
Г1U = {Г1uj / uj Î U}, где
ìГ1uj Î Г1U1 : uj Ï Г1xсв, где Г1xсв Î Г1X1,
Г1uj = íГ1uj \ xсв · X– : uj Î Uсвкext, где Г1uj Î Г1U1, Xj– = Г1uj Î Г1Uсвк,
î Г1uj Î Г1Uсвк : uj Î Uсвкint.
6. Определяем множество образов F1X вершин, для чего:
– копируем образ F1xi Î F1X1, если xi является вершиной ультраграфа HU1 и вершина xсв ей не смежна;
– добавляем к образу F1xi Î F1X1 вершины, инцидентные в куске HUсвк рёбрам uj Î Г1xi ультраграфа HU1, и удаляем вершину xсв, если xi является вершиной ультраграфа HU1 и вершина xсв ей смежна;
– добавляем к образу F1xi Î F1Xсвк вершины, инцидентные в ультраграфе HU1 ребрам uj Î Г1xi куска HUсвк, и удаляем вершину xсв, если xi является вершиной этого куска:
F1X = {F1xi / xi Î X}, где
ìF1xi : xi Î X1 & xсв Ï F1xi,
F1xi = í{F1xi · È Г2uj} \ xсв : xi Î X1 & xсв Î F1xi, Г1xi Î Г1X1, Г2uj Î Г2Uсвк,
uj Î Г1xi
î{F1xi · È Г2uj} \ xсв : xi Î Xсвк, Г1xi Î Г1Xсвк, Г2uj Î Г2U1.
ujÎГ1xi
Для первых двух выражений F1xi Î F1X1, для третьего F1xi Î F1Xсвк.
7. Формируем множество прообразов F1-1X вершин, для чего:
– копируем прообраз F1-1xi Î F1-1X1, если xi является вершиной ультраграфа HU1 и вершина xсв не принадлежит этому прообразу;
– добавляем к прообразу F1-1xi Î F1-1X1 вершины, которым инцидентны в куске HUсвк рёбра uj Î Г2xi ультраграфа HU1, и удаляем вершину xсв, если xi является вершиной ультраграфа HU1 и вершина xсв принадлежит прообразу вершины xi в ультраграф HU1;
– добавляем к образу F1-1xi Î F1-1Xсвк вершины, которым инцидентны в ультраграфе HU1 рёбра uj Î Г1xi куска HUсвк, и удаляем вершину xсв, если xi является вершиной этого куска:
F1-1X = { F1-1xi / xi Î X }, где
ìF1-1xi : xi Î X1& xсв Ï F1-1xi, F1-1xi Î F1-1X1,
F1-1xi = í{F1-1xi · È Г1uj} \ xсв : xi Î X1 & xсв Î F1-1xi,
ujÎГ2xi
î{F1-1xi · È Г1uj} \ xсв : xi Î Xсвк,
ujÎГ2xi
где для второго выражения Г2xi Î Г2X1, Г1uj Î Г1Uсвк и F1-1xi Î F1-1X1, а для третьего Г2xi Î Г2Xсвк, Г1ujÎГ1U1 и F1-1xiÎ F1-1Xсвк.
8. Создаем множество образов F2U рёбер, для чего:
– копируем образ F2uj из F2U1 ультраграфа HU1, если ребро uj принадлежит множеству его рёбер и вершина xсв не инцидентна этому ребру;
– удаляем из образа F2uj Î F2U1 рёбра, инцидентные в HU1 вершине xсв, и добавляем рёбра, инцидентные в куске HUсвк вершинам, которые принадлежат образу ребра uj в этом куске, если ребро uj Î U1 ультраграфа HU1 и вершина xсв инцидентна этому ребру;
– копируем образ F2uj из F2Uсвк куска ультраграфа HUсвк, если ребро uj принадлежит множеству его внутренних рёбер:
F2U = { F2uj / uj Î U}, где
ìF2uj : uj Î U1 & xсв Ï Г2uj,
F2uj = í{F2uj \ Г1xсв} · {È Г1xi} : uj Î U1 & xсв Î Г2uj,
xiÎXj+
îF2uj Î F2Uсвк : ujÎ Uсвкint.
Здесь: F2uj Î F2U1, Г2uj Î Г2U1, Г1xсв Î Г1U1, Г1xi Î Г1Xсвк,
Xj+ = Г2ujÎГ2Uсвк.
9. Получаем множество прообразов F2-1U рёбер, для чего:
– копируем прообраз F2-1uj из множества F2-1U1 ультраграфа HU1, если ребро uj принадлежит множеству его рёбер и вершина xсв не принадлежит множеству вершин, которым инцидентно это ребро;
– удаляем из прообраза F2-1uj Î F2-1U1 рёбра, которым инцидентна в HU1 вершина xсв, и добавляем ребра, которым в куске HUсвк инцидентны вершины, принадлежащие прообразу ребра uj в этом куске, если ребро uj Î U1 ультраграфа HU1 и вершина xсв инцидентна этому ребру;
– копируем прообраз F2-1uj из F2-1Uсвк куска ультраграфа HUсвк, если ребро uj принадлежит множеству его внутренних ребер:
F2-1U = { F2-1uj / uj Î U }, где
ìF2-1uj : uj Î U1 & xсв Ï Г1uj,
F2-1uj = í{F2-1uj \ Г2xсв} · {È Г2xi} : uj Î U1 & xсв Î Г1uj,
xi Î Xj-
îF2-1uj Î F2-1Uсвк : ujÎ Uсвкint,
здесь: F2-1uj Î F2-1U1, Г2uj Î Г2U1, Г1xсв Î Г1U1, Г1xi Î Г1Xсвк,
Xj- = Г1uj Î Г1Uсвк.
Формальное описание выполнения операции получения гиперграфа
H (X, U):
X = (X1 \ xсв) · Xсвк; U = U1 · Uсвкint;
Г1X = Г1X1 \ Г1xсв · Г1Xсвк, Г1xсв Î Г1X1;
Г2U = {Г2uj / uj Î U}, здесь
ìГ2uj Î Г2U1 : xсв Ï Г2uj,
Г2uj = íГ2uj \ xсв · Xj : uj Î Uсвкext, где Г2uj Î Г2U1, Xj = Г2uj Î Г2Uсвк,
î Г2uj Î Г2Uсвк : uj Î Uсвкint;
F1X = {F1xi / xi Î X}, где
ìF1xi : xi Î X1 & xсв Ï F1xi,
F1xi = í{F1xi · È Г2uj} \ xсв : xi Î X1& xсв Î F1xi, Г1xi Î Г1X1, Г2uj Î Г2Uсвк,
ujÎГ1xi
î{F1xi · È Г2uj} \ xсв : xi Î Xсвк, Г1xi Î Г1Xсвк, Г2uj Î Г2U1.
uj Î Г1xi
Для первых двух выражений F1xi Î F1X1, для третьего F1xi Î F1Xсвк.
F2U = {F2uj / uj Î U}, где
ìF2uj : uj Î U1 & xсв Ï Г2uj,
F2uj = í{F2uj \ Г1xсв} · {È Г1xi} \ uj : uj Î U1 & xсв Î Г2uj,
xi Î Xj
îF2uj Î F2Uсвк : ujÎ Uсвкint.
Здесь: F2uj Î F2U1, Г2uj Î Г2U1, Г1xсв Î Г1U1, Г1xi Î Г1Xсвк, Xj = Г2uj Î Г2Uсвк.
Асимптотическая оценка вычислительной сложности данной операции без формирования образов и прообразов вершин и ребер относительно предикатов смежности равна:
· в худшем О(n×m) при n > m, если|Г1xi| или|Г2xi| ограничена m либо |Г2uj| или |Г1uj| ограничена n и |Uсвкext| или |Uсвкint| ограничена m,и О(m2) при m > n, если |Uсвкext| или |Uсвкint| ограничена m;
· в лучшем О(n) при n > m, если|Г1xi|, |Г2xi|,|Uсвкext| и |Uсвкint| ограничены константой, и О(m) при m > n, если |Uсвкext| и |Uсвкint| ограничены константой.
Операция применима к куску ультра- и гиперграфа. Выполнение операции не меняет вид части графа.
Пример. Выполним декомпозицию вершины xсв ультраграфа
HU1 (X1, U1), заменяя ее куском Hсвк (Xсвк, Uсвк), (смотри рис. 12, б). Заменяемый кусок ультраграфа HUсвк показан на рис. 13, а. Напомним, что Xсвк = {x2, x3}. Используя множества аналитического представления ультраграфа HU1 и куска Hсвк из примера для операции свертки, получим следующие множества аналитического представления ультраграфа HU:
X = {x1, xсв, x4, . . ., x10} \ xсв · {x2, x3} = {x1, x4, . . ., x10, x2, x3};
U = {u1, u2, u3, u5} · {u4} = {u1, u2, u3, u5, u4};
Г1X = {Г1x1, Г1xсв, Г1x4,…, Г1x10} \ Г1xсв · {Г1x2, Г1x3} = {Г1x1, Г1x4,…, Г1x10, Г1x2, Г1x3};
Г2X = {Г2x1, Г2св, Г2x4,…, Г2x10} \ Г2xсв · {Г2x2, Г2x3} = {Г2x1, Г2x4,…, Г2x10, Г2x2, Г2x3};
Г2U: Г2u1 = {x4, xсв} \ xсв · {x2} = {x4, x2}, Г2u2 = {x5, x6, xсв} \ xсв · {x3} = {x5, x6, x3}, Г2u3 = {x7, x8}, Г2u5 = {x9, x10}, Г2u4 = {x2};
Г1U: Г1u1 = {x1}, Г1u2 = {xсв} \ xсв ·{x2} = {x2}, Г1u3 = {xсв} \ xсв · {x3} = {x3}, Г1u5 = {x4}, Г1u4 = {x3};
F1X: F1x1 = {F1x1 Î F1X1 · Г2u1 Î Г2Uсвк} \ xсв = {{x4, xсв} · {x2}} \ xсв = {x4, x2}, F1x2 = {F1x2 Î F1Xсвк · Г2u1 Î Г2U1} \ xсв = {{x3} · {x5, x6, xсв }} \ xсв = {x3, x5, x6}, F1x3 = {F1x3 Î F1Xсвк · Г2u1 Î Г2U1} \ xсв = {{x2} · {x7, x8}} \ xсв = {x2, x7, x8}, F1x4 = {x9, x10}, F1x5 = F1x6 = F1x7 = F1x8 = F1x9 = F1x10 = Æ;
F1-1X: F1-1x1 = Æ, F1-1x2 = {F1-1x2 Î F1Xсвк · Г1u1 Î Г1U1 È Г1u2 Î Г1U1} \ xсв = {{x3} · {x1} È {xсв} \ xсв = {x3, x1}, F1-1x3 = {F1-1x3 Î F1-1Xсвк · Г1u1 Î Г1U1 È Г1u2 Î Г1U1}} \ xсв = {{x2} · {x1} È {xсв}} \ xсв = {x2, x1}, F1-1x4 = {x1}, F1-1x5 = F1-1x6 = {F1-1x5 Î F1-1X1 · Г1u2 Î Г1Uсв} \ xсв = {{xсв} · {x2}} \ xсв ={x2},
F1-1x7 = F1-1x8 = {F1-1x7 Î F1-1X1 · Г1u3 Î Г1Uсв} \ xсв = {{xсв} · {x3}} \ xсв = {x3}, F1-1x9 = F1-1x10 = {x2};
F2U: F2u1 = {{u2, u3, u5} \ {u2, u3} · {u2}} = {u5, u2},
F2u2 = {{u3} \ {u2, u3}· {u3, u4}} = {u3, u4}, F2u3 = Æ, F2u4 = {u2}, F2u5 = Æ;
F2-1U: F2-1u1 = Æ, F2-1u2 = {u1} \ {u1, u2} · {u1, u4} = {u1, u4}, F2-1u3 = {u1, u2} \ {u1, u2} · {u1, u2} = {u1, u2}, F2-1u4 = {u2}, F2-1u5 = {u1}.
В результате операции H (X,U, Г1X, Г2U) = H1 (X1,U1, Г1X1, Г2U1 ∕ xсв Þ Xсвк) получим гиперграф H1 (смотри рис. 12, в), множества аналитического представления которого будут:
X = {x1, x4, . . . , x10, x2, x3};
U = {u1, u2, u3, u5, u4};
Г1X = {Г1x1, Г1x4, . . . , Г1x10, Г1x2, Г1x3};
Г1x1 = {u1}, Г1x4 = {u1, u5}, Г1x5 = Г1x6 = {u2}, Г1x7 = Г1x8 = {u3};
Г1x9 = Г1x10 = {u5}, Г1x2 = {u1, u2, u4}, Г1x3 = { u2, u3, u4};
Г2U: Г2u1 = {x1, x4, xсв} \ xсв · {x2} = {x1, x4, x2}, Г2u2 = {x5, x6, xсв } \ xсв · {x2, x3} = { x5, x6, x2, x3}, Г2u3 = {x7, x8, xсв} \ xсв · {x3} = {x7, x8, x3},
Г2u5 = {x4, x9, x10}, Г2u4 = {x2, x3}.
Дополнение части до ультраграфа HU и гиперграфа H соответственно – рис. 14. Реализует проектную операцию удаления части схемы.

Рисунок 14 – Куски ультраграфа HU2к и гиперграфа H2к (а) и (б) соответственно –результат операции дополнения куска HU1к до ультраграфа HU и куска H1к до гиперграфа H, показанных на рисунках 11, б и в соответственно
Операция имеет две модификации: получение куска HU2к ультраграфа HU или H2к гиперграфа H и получение подграфа HU2 ультраграфа или H2 гиперграфа.
Известен ультраграф HU или гиперграф H. Задается кусок ультраграфа HU1к или гиперграфа H1к для первой модификации операции и подграф ультраграфа HU1 или подграф гиперграфа H1 для второй (смотри рис. 11, б и в соответственно).
Обозначение операции:
– HU (X,U) \ HU1к (X1к,U1к) и H(X,U) \ H1к (X1к,U1к) для получения кусков ультра- и гиперграфа соответственно или
– HU (X,U) \ HU1 (X1,U1) и H(X,U) \ H1 (X1,U1) для определения подграфов ультра- и гиперграфа соответственно.
Условие корректности операции: HU1к Ç HU ≠ Æ, HU1 Ç HU ≠ Æ, H1к Ç H ≠ Æ, H1 Ç H ≠ Æ.
Результатом выполнения операции является:
– кусок ультраграфа HU2к (X2к,U2к) = HU (X,U) \ HU1к (X1к,U1к) или
– кусок гиперграфа H2к (X2к,U2к)= H(X,U) \ H1к (X1к,U1к) либо
– подграф ультраграфа HU2(X2,U2) = HU (X,U) \ HU1 (X1,U1) или
– подграф гиперграфа H2 (X2,U2)= H(X,U) \ H1 (X1,U1).
Полученный кусок или подграф может содержать несколько компонент связности. Например, если искать дополнение кусков HU2к и H2к, показанных на рис. 14, а или б соответственно, до ультраграфа HU и гиперграфа H (смотри рис. 11, б и в), результатом операции будут куски HU1к и H1к – показаны на том же рисунке, которые состоят из двух компонент связности. Как и в предыдущей операции здесь не формируется аналитическое представление каждой компоненты связности. Множества вершин, ребер, образов и прообразов (для ультраграфа) формируемой части графа представляют собой конкатенацию соответствующих множеств компонент связности, входящих в эту компоненту.
Содержательно – формальное описание результата операции дополнения куска HU1к (X1к, U1к) до куска ультраграфа HUк (Xк, Uк).
Для получения множеств куска HU2к (X2к, U2к):
1. Определяем множество X2к вершин, исключая из Xк вершины множества X1к: X2к = Xк \ X1к.
2. Формируем множество U2кint внутренних рёбер, удаляя из Uкint рёбра множества U1к куска HU1к: U2кint = Uкint \ U1к.
3. Создаем множество U2кext, добавляя в Uкext, те рёбра из Uкint, которые в куске HU1к являются внешними, и удаляя те рёбра Uкext, у которых все вершины образов и прообразов принадлежат множеству X1к:
U2кext = {Uкext È Uкint Ç U1кext} \ Ud,
где Ud = {uj : Г2uj Í X1к & Г1uj Í X1к / uj Î U кext, Г2uj Î Г2Uк, Г1uj Î Г1Uк}.
4. Образуем множество U2к, применяя операцию конкатенации к множествам U2кint и U2кext: U2к = U2кint · U2кext.
5. Формируем множество Г1X2к образов вершин куска HU2к, исключая из Г1X образы Г1X1к вершин куска HU1к:
Г1X2к = {Г1xi Î Г1Xк / xi Î X2к}.
6. Формируем множество Г2X2к прообразов вершин куска HU2к, исключая из Г2X прообразы Г2X1к вершин куска HU1к:
Г2X2к = {Г2xi Î Г2Xк / xi Î X2к}.
7. Создаем множество Г2U2к образов рёбер куска HU2к так, что образом внутреннего ребра является образ Г2uj одноименного ребра в Г2Uк, а образ внешнего ребра формируется как Г2uj \ X1к, т. е. удалением вершин, принадлежащих множеству X1к:
Г2U2к = {Г2uj : uj Î U2кint Ú Г2uj \ X1к : uj Î U2кext / uj Î U2к, Г2uj Î Г2Uк}.
8. Создаем множество Г1U2к прообразов рёбер куска HU2к так, что прообразом внутреннего ребра является прообраз Г1uj одноименного ребра в Г1Uк, а прообраз внешнего ребра формируется как Г1uj \ X1к, т. е. удалением вершин, принадлежащих множеству X1к:
Г1U2к = {Г1uj : uj Î U2кint Ú Г1uj \ X1к : uj Î U2кext / uj Î U2к, Г1uj Î Г1Uк}.
9. Получаем множества F1X2к образов и F1-1X2к прообразов вершин
xi Î X2к, удаляя при копировании из F1xi Î F1Xк и F1-1 xi Î F1-1Xк вершины не принадлежащие X2к:
F1X2к = {F1xi \ xj Ï X2к / xi Î X2к, F1xi Î F1Xк} и
F1-1X2к = {F1-1xi \ xj Ï X2к / xi Î X2к, F1-1xi Î F1-1Xк}.
10. Образуем множества F2U2к образов и F2-1U2к прообразов рёбер
uj Î U2к для чего копируем F2uj из F2Uк и F2-1uj из F2-1Uк, если uj является внутренним ребром куска HU2к, и удаляя при копировании из образа и прообраза внутренние ребра U1кint куска HU1к, если uj является внешним ребром куска HU2к:
F2U2к = {F2uj : uj Î U2кint Ú F2uj \ U1кint : uj Î U2кext / uj Î U2к, F2uj Î F2Uк};
F2-1U2к = {F2-1uj : uj Î U2кint Ú F2-1uj \ U1кint : uj Î U2кext / uj Î U2к,
F2-1uj Î F2-1Uк}.
Для операции «Дополнение куска до ультраграфа» пункты 2 и 3 будут иметь вид:
2. Формируем множество U2кint внутренних ребер, удаляя из U ребра множества U1к куска HU1к: U2кint = U \ U1к.
3. Копируем множество U1кext под именем U2кext: U2кext = U1кext.
Формальное описание результата операции в виде куска гиперграфа H2к (X2к, U2к):
X2к = X \ X1к; U2кint = U \ U1к; U2кext = U1кext; U2к = U2кint · U2кext;
Г1X2к = Г1X \ Г1X1к = {Г1xi Î Г1X/ xi Î X2к};
Г2U2к = {Г2uj : uj Î U2кint Ú Г2uj \ X1к : uj Î U2кext / uj Î U2к, Г2uj Î Г2U};
F1X2к = {F1xi \ xj Î X1к / xi Î X2к, F1xi Î F1X };
F2U2к = {F2uj : uj Î U2кint Ú F2uj \ U1кint : uj Î U2кext / uj Î U2к, F2uj Î F2U}.
Аналитическое представление подграфа HU2 ультраграфа или подграфа H2 гиперграфа получаем по тем же формулам, что и для подграфа HU1 ультраграфа и подграфа H1 гиперграфа в операции «Формирование части ультраграфа HU1 или гиперграфа H1», определяя X2 = X \ X1 и заменяя в остальных выражениях X1 на X2 и U1 на U2.
Асимптотическая оценка вычислительной сложности данной операции без учета операций формирования образов и прообразов вершин и рёбер относительно предикатов смежности равна:
· в худшем О(n2×m), если |U2кext| ограничены m, а |Г2uj| и |X1к| ограничены n;
· в лучшем О(1), если |X1к |, |U2кext| и |Г2uj| ограничены константой.
Вычислительная сложность операции над гиперграфом имеет тот же порядок.
Операция может выполняться и для «дополнения куска до куска».
Пример. В примере предыдущей операции из схемы, показанной на рис. 11, а, выделена часть, включающую элементы э1, э2, э3, э4, э5 и сформирован кусок ультраграфа HU1к (смотри рис. 11, б).
В результате операции HU2к (X2к,U2к) = HU (X, U) \ HU1к (X1к, U1к) получим кусок ультраграфа HU2к, показанный на рис. 14, а, в котором:
X2к = {x6, x7, x8, x9, x10, x11};
U2кint = {u2, u5}, U2кext = {u3, u1}; U2к = {u2, u5, u3, u1};
Г1X2к = {{u2},{u5}, Æ, Æ, Æ, Æ};
Г2X2к = {{u1},{u2},{u2},{u5},{u3},{u3, u5}};
Г2U2к: Г2u2 = {x7, x8}, Г2u5 = {x9, x11}, Г2u3 = {x10, x11} \ X1к = {x10, x11},
Г2u1 = {x3, x6} \ X1к = {x6};
F1X2к: F1x6 = {x7, x8}, F1x7 = {x9, x11}, F1x8 = F1x9 = F1x10 = F1x11 = Æ;
F1-1X2к: F1-1x6 = {x4} \ {x4} = Æ, F1-1x7 = {x6}, F1-1x8 = {x6}, F1-1x9 = {x7},
F1-1x10 = {x2} \ {x2} = Æ, F1-1x11 = {x2, x7} \ {x2} = {x7};
F2U2к: F2u2 = {u5}, F2u5 = Æ, F2u3 = Æ, F2u1 = {u2} \ {u4} = {u2};
F2-1U2к: F2-1u2 = {u1}, F2-1u5 = {u2}, F2-1u3 = {u4} \ {u4} = Æ.
Кусок гиперграфа H2к (X2к, U2к, Г1X2к, Г2U2к) – рис. 14, б:
X2к = {x6, x7, x8, x9, x10, x11};
U2кint = {u2, u5}, U2кext = {u3, u1}, U2к = {u2, u5, u3, u1};
Г1X2к = {{u1, u2}, {u2,u5}, {u2}, {u5}, {u3}, {u3, u5}};
Г2U2к: Г2u2 = {x6, x7, x8}, Г2u5 = {x7, x9, x11};
Г2u3 = {x2, x10, x11} \ X1к = {x10, x11}, Г2u1 = {x3, x4, x6} \ X1к = {x6}.
Объединение частей ультраграфа или гиперграфа. Реализует проектную операцию объединения двух схем, имеющих общие элементы и/или цепи. Операция приводит к образованию одной компоненты связности при выполнении указанных в таблице 3 условий, если объекты объединения представляют собой одну компоненту связности каждый. В качестве объектов операции могут выступать куски графов и подграфы. На рис. 15 показан пример объединения двух кусков ультраграфа (HU1к и HU2к) и гиперграфа (H1к и H2к). Возможные варианты объединения частей графов представлены в таблице 3, в которой X1к, X2к, U1к, U2к и X1, X2, U1, U2 – множества вершин и рёбер куска графа и подграфа соответственно.
Таблица 3
|
N |
Объединяемые части |
Возможные варианты |
Вид результата |
|
1 |
Два куска HU1к и HU2к ультраграфа HU (X, U) или H1к и H2к гиперграфа H (X, U) такие, что X1к Ç X2к = X |
X1к Ç X2к ¹ Æ, U1к Ç U2к ¹ Æ; X1к Ç X2к ¹ Æ, U1к Ç U2к = Æ; |
кусок, если U1кext ¹ U2кext, граф, если U1кext = U2кext кусок графа |
|
2 |
Кусок и подграф тех же абстракций |
X1к Ç X2 ¹ Æ, U1к Ç U2 ¹ Æ; X1к Ç X2¹ Æ, U1к Ç U2 = Æ; |
кусок графа |
|
3 |
Два подграфа тех же абстракций |
X1 Ç X2 ¹ Æ, U1 Ç U2 ¹ Æ; X1 Ç X2 ¹ Æ, U1 Ç U2 = Æ; |
граф |

Рисунок 15 – Соединяемые фрагменты (а) и полученная схема (б), модели фрагментов в виде кусков ультраграфа HU1к и HU2к (в) и ультраграф HU результата операции (г), модели фрагментов в виде кусков гиперграфа H1к и H2к(д), гиперграф H результата
операции (е)
Задаются аналитически две части ультраграфа или гиперграфа, например куски HU1к (X1к, U1к) и HU2к (X2к, U2к) или H1к (X1к, U1к) и H2к (X2к, U2к). Куски графов (подграфы) могут содержать несколько компонент связности как на рис. 15 кусок ультраграфа HU1к или гиперграфа H1к. В этом случае множества аналитического задания части графа должны представлять собой конкатенацию соответствующих множеств его компонент связности.
Обозначение операции состоит из символа операции È, соединяющего имена ее объектов. Например, объединение двух кусков ультраграфа –
HU1к (X1к, U1к) È HU2к (X2к, U2к) или его куска и подграфа – HU1к (X1к, U1к) È HU2 (X2, U2), двух кусков гиперграфа – H1к (X1к, U1к) È H2к (X2к, U2к) и т. д.
Условие корректности операции: X1 Ç X2 ¹ Æ Ú X1 Ç X2 = Æ &
U1 Ç U2 ¹ Æ (здесь под X1, X2, U1, U2 следует понимать соответствующие множества объединяемых компонент). В результате выполнения операции получаем одну компоненту связности.
Результат выполнения операции указан в таблице 3. При объединении, например куска и подграфа ультраграфа получим ультраграф
HUк (Xк, Uк) = HU1к (X1к, U1к) È HU2 (X2, U2).
Общее формальное описание результата операции.
Приведенные ниже формулы получены для общего случая, когда у объединяемых частей графа пересечение множеств вершин не пусто и пересечение множеств рёбер также не пусто и результатом операции является ультра- или гиперграф.
Для ультраграфа HU (X, U) получим:
X = X1 È X2; U = U1 È U2;
Г1X = {Ui1+ È Ui2+ / Ui1+ = Г1xi Î Г1X1, Ui2+ = Г1xi Î Г1X2, xi Î X};
Г2X = {Ui1– È Ui2– / Ui1– = Г2xi Î Г2X1, Ui2– = Г2xi Î Г2X2, xi Î X};
Г2U = {Xj1+ È Xj2+ / Xj1+ = Г2uj Î Г2U1, Xj2+ = Г2uj Î Г2U2, uj Î U};
Г1U = { Xj1– È Xj2– / Xj1– = Г1uj Î Г1U1, Xj2– = Г1uj Î Г1U2, uj Î U}.
Здесь под X1, X2, U1, U2 и др. следует понимать соответствующие множества объединяемых компонент для конкретного варианта из рассмотренных в таблице 3. Другие обозначения:
Ui1+ = Г1xi Î Г1X1, Ui2+ = Г1xi Î Г1X2 и Ui1– = Г2xi Î Г2X1, Ui2– = Г2xi Î Г2X2 – множества рёбер, инцидентных вершине xi, и рёбер, которым инцидентна эта вершина, в графах H1 и H2 соответственно;
Xj1+ = Г2uj Î Г2U1, Xj2+ = Г2uj Î Г2U2 и Xj1– = Г1uj Î Г1U1, Xj2– = Г1uj Î Г1U2 – множества вершин, инцидентных ребру uj, и вершин, которым инцидентно это ребро, в графах H1 и H2 соответственно.
Формальное описание множеств гиперграфа H (X, U):
X = X1 È X2; U = U1 È U2;
Г1X = {Ui1 È Ui2 / Ui1 = Г1xi Î Г1X1, Ui2 = Г1xi Î Г1X2, xi Î X};
Г2U = {Xj1 È Xj2 / Xj1 = Г2uj Î Г2U1, Xj2 = Г2uj Î Г2U2, uj Î U}.
В практике автоматизированного проектирования наиболее часто встречающейся процедурой является объединение двух схем, не имеющих общих элементов, внешние цепи которых полностью или частично совпадают. Реализация этой процедуры операцией объединения моделей этих схем в виде ультра- или гиперграфа на основе указанных выше выражений приведет к лишним затратам машинного времени (например X1 Ç X2 = Æ, а определяется X как X1 È X2). Для таких вариантов целесообразно конкретизировать формальное описание результата операции. Ниже это сделано для операции объединения двух кусков ультраграфа и гиперграфа, у которых
X1к Ç X2к = Æ, U1кext = U2кext и U1кint Ç U2кint = Æ.
Содержательно – формальное описание результата операции
HU (X, U) = HU1к (X1к, U1к) È HU2 (X2к, U2к).
Для получения ультраграфа HU (X, U):
1. Определяем множество вершин X, копируя множества X1к и X2к и соединяя их, так как по условию X1к Ç X2к = Æ: X = X1к · X2к.
2. Формируем множество U ребер, занося в него ребра множеств U1кint, U2кint и U1кext:
U = U1кint · U2кint · U1кext.
3. Создаем множество образов Г1X и прообразов Г2X вершин ультраграфа HU, соединяя при копировании множества Г1X1к и Г1X2к и Г2X1к и Г2X2к соответственно, так как при X1к Ç X2к = Æ, если Г1xi Î Г1X1к, то Г1xi Ï Г1X2к и наоборот, и если Г2xi Î Г2X1к, то Г2xi Ï Г2X2к и наоборот:
Г1Xк = Г1X1к · Г1X2к, Г2Xк = Г2X1к · Г2X2к.
4. Формируем множество Г2U образов рёбер, занося в него:
– образ Г2uj из множества Г2U1к образов куска HU1к, если uj является его внутренним ребром,
– образ Г2uj из множества Г2U2к образов куска HU2к, если uj является его внутренним ребром,
– соединение (конкатенацию) множеств, являющихся образамиребра uj в Г2U1к и Г2U2к, если оно принадлежит U1кext = U2кext:
Г2U = {Г2uj / uj Î U }, где
ìГ2uj Î Г2U1к, если uj Î U1кint,
Г2uj = íГ2uj Î Г2U2к, если uj Î U2кint,
îXj1+ · Xj2+, если uj Î U1кext, где Xj1+ = Г2uj Î Г2U1к , Xj1+ Í X1к,
Xj2+ = Г2uj Î Г2U2к, Xj2+ Í X2к.
5. Создаем множество Г1U прообразов рёбер, занося в него:
– прообраз Г1uj из множества Г1U1к прообразов куска HU1к, если uj является его внутренним ребром,
– прообраз Г1uj из множества Г1U2к прообразов куска HU2к, если uj является его внутренним ребром,
– соединение (конкатенацию) множеств, являющихся прообразами ребра uj в Г1U1к и Г1U2к, если оно принадлежит U1кext = U2кext:
Г1U = {Г1uj / uj Î U }, где
ìГ1uj Î Г1U1к, если uj Î U1кint,
Г1uj = íГ1uj Î Г1U2к , если uj Î U2кint,
îXj1– · Xj2–, если uj Î U1кext, где Xj1– = Г1uj Î Г1U1к, Xj1– Í X1к,
Xj2– = Г1uj Î Г1U2к, Xj2– Í X2к.
10. Определяем множество F1X образов вершин относительно предиката смежности F1(X, X). Для вершины xi Î X1к Ì X копируем ёё образ из F1X1к, если ей не инцидентно ни одно из внешних ребер куска HU1к, в противном случае к этому образу добавляем вершины, принадлежащие множеству X2к, которые инцидентны ребрам подмножества Ui' = Г1xi Ç U1кext. Аналогично определяем образы вершин xi Î X2к Ì X:
F1X = {F1xi / xi Î X }, где
для xi Î X1к Ì X:
ìF1xi : Г1xi Ç U1кext = Æ,
F1xi = í
îF1xi · {È Г2uj} : Г1xi Ç U1кext ¹ Æ, где Ui' = Г1xi Ç U1кext,
uj Î Ui'
здесь: F1xi Î F1X1к, Г2uj Î Г2U2к, Г1xi Î Г1X1к
и для xi Î X2к Ì X:
ìF1xi : Г1xi Ç U2кext = Æ,
F1xi = í
îF1xi · {È Г2uj} : Г1xi Ç U2кext ¹ Æ, где Ui' = Г1xi Ç U2кext,
uj Î Ui'
здесь: F1xi Î F1X2к, Г2uj Î Г2U1к, Г1xi Î Г1X2к.
11. Формируем множество F1-1X прообразов вершин. Для вершины xi Î X1к Ì X копируем ёё прообраз из F1-1X1к, если она не инцидентна ни одному из внешних рёбер куска H1к, в противном случае к этому прообразу добавляем вершины, принадлежащие множеству X2к, которым инцидентны рёбра подмножества Ui' = Г2xi Ç U1кext. Аналогично определяем образы вершин xi Î X2к Ì X:
F1-1X = { F1-1xi / xi Î X }, где
для xi Î X1к Ì X:
ìF1-1xi : Г2xi Ç U1кext = Æ,
F1-1xi = í
îF1-1xi · {È Г1uj} : Г2xi Ç U1кext ¹ Æ, где Ui' = Г2xi Ç U1кext,
uj Î Ui'
здесь: F1-1xi Î F1-1X1к, Г1uj Î Г1U2к, Г2xi Î Г2X1к
и для xi Î X2к Ì X:
ìF1-1xi : Г2xi Ç U2кext = Æ,
F1-1xi = í
îF1-1xi · {È Г1uj} : Г2xi Ç U2кext ¹ Æ, где Ui' = Г2xi Ç U2кext,
uj Î Ui'
здесь: F1xi Î F1X2к, Г1uj Î Г1U1к, Г2xi Î Г2X2к .
12. Создаем множество F2U образов рёбер относительно предиката смежности F2(U, U), копируя образ F2uj из множества образов куска HU1к, если ребро uj является внутренним ребром первого куска, или из множества образов куска H2к, если ребро uj является внутренним ребром второго куска. Если ребро uj является внешним, то образ получаем конкатенацией его образов в кусках HU1к и HU2к:
F2U = {F2uj / uj Î U }, здесь
ìF2uj : uj Î U1кint, F2uj Î F2U1к,
F2uj = íF2uj : uj Î U2кint, F2uj Î F2U2к,
îU1j+ · U2j+ : uj Î U1кext,
где U1j+ = F2uj Î F2U1к, U1j+ Í U1к, U2j+ = F2uj Î F2U2к, U2j+ Í U2к.
13. Формируем множество F2-1U прообразов рёбер, копируя прообраз F2-1uj из множества прообразов куска HU1к, если ребро uj является внутренним ребром первого куска, или из множества прообразов куска HU2к, если ребро uj является внутренним ребром второго куска. Если ребро uj является внешним, то прообраз получаем конкатенацией его прообразов в кусках HU1к и HU2к:
F2-1U = {F2-1uj / uj Î U }, где
ìF2-1uj : uj Î U1кint, F2-1uj Î F2-1U1к,
F2-1uj = í F2-1uj : uj Î U2кint, F2-1uj Î F2-1U2к,
îU1j– · U2j– : uj Î U1кext, где U1j– = F2-1uj Î F2-1U1к , U1j– Í U1к,
U2j– = F2-1uj Î F2-1U2к, U2j– Í U2к.
Формальное описание результата операции в виде гиперграфа
H (X, U, Г1X, Г2U) при X1к Ç X2к = Æ, U1кint Ç U2кint = Æ и U1кext = U2кext:
X = X1к · X2к; U = U1кint · U2кint · U1кext;
Г1X = Г1X1к · Г1X2к;
Г2U = {Г2uj / uj Î U}, где
ìГ2uj Î Г2U1к, если uj Î U1кint,
Г2uj = íГ2uj Î Г2U2к, если uj Î U2кint,
îXj1 · Xj2 , если uj Î U1кext, где Xj1 = Г2uj Î Г2U1к , Xj2 = Г2uj Î Г2U2к;
F1X = { F1xi / xi Î X }, где
ìF1xi : Г1xi Ç U1кext = Æ,
F1xi = í
îF1xi · {È {Г2uj \ xi }} : Г1xi Ç U1кext ¹ Æ, где Ui' = Г1xi Ç U1кext,
uj Î Ui'
здесь: F1xi Î {F1X1к, F1X2к}, Г1xi Î {Г1X1к, Г1X2к}, Г2uj Î {Г2U1к, Г2U2к};
F2U = {F2uj / uj Î U }, здесь
ìF2uj : uj Î U1кint Ú uj Î U2кint, где F2uj Î {F2U1к, F2U2к},
F2uj = í
îU1j · U2j : uj Î U1кext, где U1j = F2uj Î F2U1к, U2j = F2uj Î F2U2к.
Формальное описание результата операции в виде куска
ультраграфа HUк (Xк, Uк).
Кусок ультраграфа получим, если U1кext ¹ U2кext. Так как по условию
X1к Ç X2к = Æ, U1кint Ç U2кint = Æ, множества вершин, их образов и прообразов относительно предиката инцидентности Г1(X, U) куска ультраграфа определяются по тем же формулам, что и для ультраграфа HU. Остальные множества получаем по формулам:
Uк = U1кint · U2кint · {U1кext È U1кext}, Uкext = U1кext D U2кext,
U кint = U1кint · U2кint;
Г2Uк = {Г2uj / uj Î Uк}, здесь
ìГ2uj Î Г2U1к : uj Î U1кint Ú (uj Î U1кext & uj Ï U2кext),
Г2uj = íГ2uj Î Г2U2к : uj Î U2кint Ú (uj Î U2кext & uj Ï U1кext),
îXj1+ · Xj2+ : uj Î {U1кext Ç U2кext},
где Xj1+ = Г2uj Î Г2U1к, Xj2+ = Г2uj Î Г2U2к;
Г1Uк = {Г1uj / uj Î Uк}, здесь
ìГ1uj Î Г1U1к : uj Î U1кint Ú (uj Î U1кext & uj Ï U2кext),
Г1uj = íГ1uj Î Г1U2к : uj Î U2кint Ú (uj Î U2кext & uj Ï U1кext),
îXj1– · Xj2– : uj Î {U1кext Ç U2кext},
где Xj1– = Г1uj Î Г1U1к, Xj2– = Г1uj Î Г1U2к;
F1X = {F1xi / xi Î X }, здесь
ìF1xi : Г1xi Ç Uextп = Æ, где Uextп = U1кext Ç U2кext,
F1xi = í
îF1xi · {È Г2uj}: Г1xi Ç Uextп ¹ Æ,
uj Î Uextп
F1xi Î {F1X1к, F1X2к}, Г2uj Î {Г2U1к, Г2U2к}, Г1xi Î {Г1X1к, Г1X1к};
F1-1X = {F1-1xi / xi Î X}, здесь
ìF1-1xi : Г2xi Ç Uextп = Æ,
F1-1xi = í
îF1-1xi · {È Г1uj} : Г2xi Ç Uextп ¹ Æ,
uj Î Uextп
где Uextп то же, что и выше, F1-1xi Î {F1-1X1к, F1-1X2к}, Г1uj Î{Г1U1к, Г1U2к},
Г2xi Î {Г2X1к, Г2X1к};
F2Uк = {F2uj / uj Î Uк}, здесь
ìF2uj : uj Ï Uextп, где F2uj Î {F2U1к, F2U1к},
F2uj = í
îU1j+ · U2j+ : uj Î Uextп, где Uextп – то же, что и выше, U1j+ = F2uj Î F2U1к, U2j+ = F2uj Î F2U2к;
F2-1Uк = {F2-1uj / uj Î U к}, здесь
ìF2-1uj : uj Ï Uextп, где F2-1uj ÎF2-1U1к, F2-1U1к},
F2-1uj = í
îU1j– · U2j– : uj Î Uextп, где Uextп – то же, что и выше, U1j– = F2-1uj Î F 2-1U1к, U2j– = F2-1uj Î F2-1U2к.
Формальное описание результата операции в виде куска гиперграфа Hк (Xк, Uк) при X1к Ç X2к = Æ, U1кint Ç U2кint = Æ и U1кext ¹ U2кext.
Множества вершин и их образов относительно предиката инцидентности Г1(Xк, Xк) куска гиперграфа определяются по тем же формулам, что и для гиперграфа H. Остальные множества получаем по формулам:
Uк = U1кint · U2кint · {U1кext È U1кext},
Uкext = U1кext D U2кext, Uкint = U1кint · U2кint;
Г2Uк = {Г2uj / uj Î Uк}, здесь
ìГ2uj Î Г2U1к : uj Î U1кint Ú (uj Î U1кext & uj Ï U2кext),
Г2uj = íГ2uj Î Г2U2к : uj Î U2кint Ú (uj Î U2кext & uj Ï U1кext),
îXj1 · Xj2 : uj Î Uextп,
где Uextп = U1кext Ç U2кext, Xj1 = Г2uj Î Г2U1к, Xj2 = Г2uj Î Г2U2к;
F1X = {F1xi / xi Î Xк}, здесь
ìF1xi : Г1xi Ç Uextп = Æ,
F1xi = í
îF1xi · È {Г2uj \ xi } : Г1xi Ç Uextп ¹ Æ,
uj Î Uextп
где Uextп – то же, что и выше, F1xi Î {F1X1к, F1X2к}, Г2uj Î {Г2U1к, Г2U2к},
Г1xi Î {Г1X1к, Г1X1к};
F2Uк = {F2uj / uj Î Uк}, здесь
ìF2uj : uj Ï Uextп, где F2uj Î {F2U1к, F2U1к},
F2uj = í
îU1j · U2j : uj Î Uextп,
где F2uj Î {F2U1к, F2U1к}, Uextп – то же, что и выше, U1j = F2uj Î F2U1к ,
U2j = F2uj Î F2U2к.
Асимптотическая оценка вычислительной сложности данной операции, если результатом является ультраграф HU или гиперграф H, равна О(m× n) при n > m или О(m2) при m > n.
Пример. Результатом операции объединения двух кусков ультраграфа HU1к (X1к, U1к) и HU2к (X2к, U2к), изображенных на рис. 15, в , если считать, что у куска HU2к нет ребра u6, будет ультраграф HU (X, U), показанный на рис.15, г, так как U1кext = U2кext = {u1, u3}. В соответствии с приведенными выше выражениями получим:
X = {x1, x2, . . ., x10}; U = {u4} · {u2, u5}·{u1, u3} = {u4, u2, u5, u1, u3};
Г1X: Г1x1 = {u4}, Г1x2 = {u3}, Г1x3 = Æ, Г1x4 = {u1}, Г1x5 = Æ, Г1x6 = {u2}, Г1x7 = {u5}, Г1x8 = Г1x9 = Г1x10 = Æ;
Г2X: Г2x1 = Æ, Г2x2 = {u4}, Г2x3 = {u1}, Г2x4 = Æ, Г2x5 = {u4}, Г2x6 = {u1}, Г2x7 = Г2x8 = Æ, Г1x9 = {u3, u5}, Г1x10 = {u3};
Г2U: Г2u4 = {x2, x5}, Г2u2 = {x7, x8}, Г2u5 = {x9}, Г2u1 = {x3} · {x6} = {x3, x6}, Г2u3 = Æ · {x9, x10} = { x9, x10};
Г1U: Г1u4 = {x1}, Г1u2 = {x6}, Г1u5 = {x7}, Г1u1 = {x4} · Æ = {x4},
Г1u3 = {x2} · Æ = {x2};
F1X: F1x1 = {x2, x5}, F1x2 = Æ · Г2u3 = { x9, x10}, F1x3 = Æ, F1x4 = {x3} · Г2u1 = {x3, x6}, F1x5 = Æ, F1x6 = {x7, x8}, F1x7 = {x9}, F1x8 = F1x9 = F1x10 = Æ;
F1-1X: F1-1x1 = Æ, F1-1x2 = {x1}, F1-1x3 = {x4} · Æ = {x4}, F1-1x4 = Æ, F1-1x5 = {x1}, F1-1x6 = Æ · {x4} = {x4}, F1-1x7 = F1-1x8 = {x6}, F1-1x9 = F1-1x10 = Æ · Г1u3 = {x2};
F2U: F2u4 = {u3}, F2u2 = {u5}, F2u5 = Æ, F2u1 = Æ · {u2} = {u2}, F2u3 = Æ;
F2-1U: F2-1u4 = Æ, F2-1u2 = {u1}, F2-1u5 = {u2}, F2-1u1 = Æ, F2-1u3 = {u4} · Æ = {u4}.
При объединении кусков гиперграфа, показанных на рис. 15, д, (считаем, что у куска H2к нет ребра u6), получаем в результате операции
H (X, U, Г1X, Г2U) = H1к (X1к,U1к, Г1X1к, Г2U1к) È H2к (X2к,U2к, Г1X2к, Г2U2к), гиперграф H (X, U, Г1X, Г2U), у которого:
X = {x1, x2, . . ., x10}; U = {u4, u2, u5, u1, u3};
Г1X: Г1x1 = Г1x5 = {u4}, Г1x2 = {u3, u4}, Г1x3 = Г1x4 = {u1}, Г1x6 = {u1, u2}, Г1x7 = {u2, u5}, Г1x8 = {u2}, Г1x9 = {u3, u5}, Г1x10 = {u3};
Г2U: Г2u4 = {x1, x2, x5}, Г2u2 = { x6, x7, x8}, Г2u5 = {x7, x9}, Г2u1 = {x3, x4} · {x6} = {x3, x4, x6}, Г2u3 = {x2} · {x9, x10} = {x2, x9, x10}.
Объединение кусков, изображенных на рис. 15, д, если у куска H2к будет ребро u6, дает кусок гиперграфа Hк (Xк, Uк, Г1Xк, Г2Uк), у которого:
Xк = X; Uк = {u4, u2, u5, u1, u3, u6}– в куске H2к появилось внешнее ребро u6; в Г1Xк по сравнению с Г1X изменится образ вершины x7 – Г1x7 = {u2, u5, u6} и в Г2Uк по сравнению с Г2U появится образ ребра u6 – Г2u6 = {x7}. Множество внешних ребер куска Uкext = {u1,u3} D {u1,u3,u6} = {u6}, множество внутренних ребер очевидно.
Пересечение ультраграфов HU1 и HU2 или гиперграфов H1 и H2 – рис. 16. Реализует проектную операцию проверки идентичности двух представлений схемы или определения одинаковых частей схем при совпадающих идентификаторах их элементов и цепей.
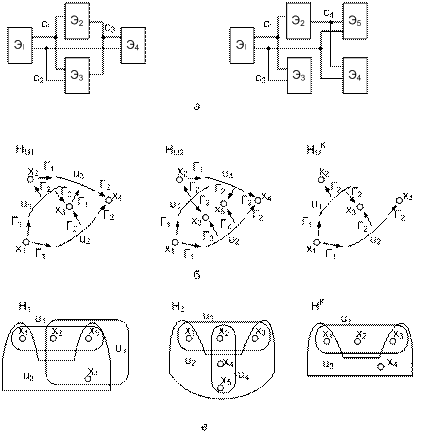
Рисунок 16 – Фрагменты схем а, их модели в виде ультраграфов HU1 и HU2 и результат HU операции их пересечения (б); модели фрагментов в виде гиперграфов H1 и H2 и результат H операции их пересечения (в)
Задаются в аналитической форме два ультраграфа HU1 и HU2 или гиперграфа H1 и H2.
Обозначение операции: HU1 (X1, U1) Ç HU2 (X2, U2) для ультраграфов и
H1 (X1, U1) Ç H2 (X2, U2) для гиперграфов.
Условие корректности операции X1 Ç X2 ¹ Æ, U1 Ç U2 ¹ Æ, а также:
– для ультраграфа $ uj Î {U1 Ç U2} (Xj1+ Ç Xj2+ ¹ Æ Ú Xj1– Ç Xj2– ¹ Æ),
где аналогично операции объединения частей графов Xj1+ = Г2uj Î Г2U1 и Xj2+ = Г2uj Î Г2U2 вершины, инцидентные ребру uj в ультраграфе HU1 и HU2 соответственно, Xj1– = Г1uj Î Г1U1 и Xj2– = Г1uj Î Г1U2 вершины, которым инцидентно ребро uj в ультраграфе HU1 и HU2 соответственно,
– для гиперграфа $ uj Î {U1 Ç U2} (Xj1 Ç Xj2 ¹ Æ),
где Xj1 = Г2uj Î Г2U1, Xj2 = Г2uj Î Г2U2.
Результатом выполнения операции может быть ультраграф, кусок ультраграфа или несколько компонент связности: ультраграфы, куски ультраграфов, их сочетание (сказанное справедливо и по отношению к гиперграфам). Полагая отдельной задачу определения количества компонент связности, дадим описание операции для одной компоненты в виде ультраграфа HU (X, U) или его куска HUк (Xк, Uк, Г1Xк, Г2Uк), а также гиперграфа H (X, U) или его куска Hк (Xк, Uк, Г1Xк, Г2Uк).
В результате выполнеия операции получим:
– ультраграф HU (X, U) = HU1 (X1, U1) Ç HU2 (X2, U2), если
"uj Î {U1 Ç U2} (Xj1+ = Xj2+ & Xj1– = Xj2–) (16),
– кусок ультраграфа HUк (Xк, Uк) = HU1 (X1, U1) Ç HU2 (X2, U2), если
$ uj Î {U1 Ç U2} (Xj1+ ¹ Xj2+ Ú Xj1– ¹ Xj2–), где Xj1+, Xj2+, Xj1–, Xj2– то же, что и выше;
– гиперграф H (X, U) = H1 (X1, U1) Ç H2 (X2, U2), если
" uj Î {U1 Ç U2} (Xj1 = Xj2),
– кусок гиперграфа Hк (Xк, Uк) = H1 (X1, U1) Ç H2 (X2, U2), если
$ uj Î {U1 Ç U2} (Xj1 ¹ Xj2), где Xj1 и Xj2 – то же, что и выше.
Содержательно – формальное описание результата операции над ультраграфами HU1 (X1, U1) и HU2 (X2, U2).
Для получения множеств ультраграфа HU (X, U):
1. Определяем множества вершин X и ребер U, находя общие элементы множеств X1, X2 и U1, U2 соответственно:
X = X1 Ç X2; U= U1 Ç U2.
2. Создаем множества образов Г1X и прообразов Г2X вершин ультраграфа, занося в образ и прообраз каждой вершины общие ребра ее образов и прообразов в ультраграфах HU1 и HU2:
Г1X = {Г1xi = Ui1+ Ç Ui2+ / xi Î X, Ui1+ = Г1xi Î Г1X1, Ui2+ = Г1xi Î Г1X2};
Г2X = {Г2xi = Ui1– Ç Ui2– / xi Î X, Ui1– = Г2xi Î Г2X1, Ui2– = Г2xi Î Г2X2},
где аналогично операции объединения частей графа Ui1+ = Г1xi Î Г1X1, Ui2+ = Г1xi Î Г1X2 и Ui1– = Г2xi Î Г2X1, Ui2– = Г2xi Î Г2X2 – множества ребер, инцидентных вершине xi, и множества ребер, которым инцидентна этавершина, в ультраграфах HU1 и HU2 соответственно.
3. Формируем множество образов Г2U и прообразов Г1U рёбер, определяя общие вершины их образов и прообразов соответственно в ультраграфах HU1 и HU2:
Г2U = {Xj1+ Ç Xj2+ / uj Î U}, где Xj1+ и Xj2+ – то же, что и выше;
Г1U = {Xj1– Ç Xj2– / uj Î U, Г1uj Î Г1U1},где Xj1– и Xj2–– то же, что и выше.
4. Находим образы F1xi вершин как объединение общих вершин образов рёбер, инцидентных вершине xi как в ультраграфе HU1, так и в ультраграфе HU2:
F1X = { È Xj1+ Ç Xj2+ / xi Î X }, где Uiп+ = Ui1+ Ç Ui2+ и Ui1+, Ui2+,
ujÎUiп+
Xj1+, Xj2+ – то же, что и выше.
5. Определяем прообразы F1-1xi вершин как объединение общих вершин прообразов ребер, котрым инцидентна вершина xi как в ультраграфе HU1, так и в ультраграфе HU2:
F1-1X = { È Xj1– Ç Xj2– / xi Î X}, где Uiп– = Ui1– Ç Ui2– и Ui1–, Ui2–, Xj1–, Xj2– –
ujÎUiп–
то же, что и выше.
6. Формируем образы F2uj рёбер как объединение общих ребер образов вершин, инцидентных ребру uj как в ультраграфе HU1, так и в ультраграфе HU2:
F2U = { È Ui1+ Ç Ui2+ / uj Î U}, где Xjп+ = Xi1+ Ç Xi2+ и Xj1+, Xj2+, Ui1+, Ui2+
xi Î Xjп+
– то же, что и выше.
7. Находим прообразы F2-1uj как объединение общих рёбер прообразов вершин, которым инцидентно ребро uj как в ультраграфе HU1, так и в ультраграфе HU2:
F2-1U = { È Ui1– Ç Ui2– / uj Î U}, где Xjп– = Xi1– Ç Xi2– и Xj1–, Xj2–, Ui1–, Ui2–
xi Î Xjп–
– то же, что и выше.
Кусок ультраграфа HUк (Xк, Uк). Множества вершин, ребер, их образов и прообразов куска ультраграфа определяются по тем же формулам, что и для ультраграфа HU (X, U). В множество внутренних Uкint ребер куска включаем те его ребра, у которых совпадают образы и прообразы в ультраграфах HU1 и HU2. Множество внешних Uкext ребер определяем, исключая внутренние из Uк.
Uкint = {uj Î U : Xj1+ = Xj2+ & Xj1– = Xj2–}, где Xj1+, Xj2+, Xj1–, Xj2– – то же, что и выше, Uкext = Uк \ U кint.
Формальное описание результата выполнения операции над
гиперграфами H1 (X1, U1) и HU2 (X2, U2).
Гиперграф H (X, U):
X = X1 Ç X2; U = U1 Ç U2;
Г1X = {Г1xi = Ui1 Ç Ui2 / xi Î X, Ui1 = Г1xi Î Г1X1, Ui2 = Г1xi Î Г1X2};
Г2U = {Xj1 Ç Xj2 / uj Î U}, где Xj1 и Xj2 – то же, что и выше;
F1X = { È Xj1¢ Ç Xj2¢ / xi Î X }, где Uiп = Ui1 Ç Ui2 и Ui1, Ui2 – то же, что
ujÎUiп
и выше, и Xj1¢ = {Г2uj \ xi : |Г2uj| > 1 Ú Г2uj : |Г2uj| = 1}, Г2uj Î Г2U1,
Xj2¢ = {Г2uj \ xi : |Г2uj| > 1 Ú Г2uj : |Г2uj| = 1}, Г2uj Î Г2 U2;
F2U = { È Ui1¢ Ç Ui2¢ / uj Î U}, где Xjп = Xi1 Ç Xi2 и Xj1, Xj2– то же, что и
xi Î Xjп
выше, и Ui1¢ = {Г1xi \ uj : |Г2uj| > 1 Ú Г1xi : | Г2uj| = 1}, Г1xi Î Г1X1,
Ui2¢ = {Г1xi \ uj : |Г2uj| >1 Ú Г1xi : | Г2uj| = 1}, Г1xi Î Г1X2.
Кусок гиперграфа H к (Xк, Uк). Множества вершин, ребер и образов вершин куска гиперграфа определяются по тем же формулам, что и для гиперграфа H (X, U). Множества внутренних и внешних ребер будут:
Uкint = {uj Î U : Xj1 = Xj2 / Xj1 = Г2uj Î Г2U1, Xj1 = Г2uj Î Г2U2},
Uкext = Uк \ Uкint.
Асимптотическая оценка вычислительной сложности операции для ультра- и гиперграфов равна:
· в худшем О(m2× n) ,если |Ui1+| и |Ui2+| или |Ui1–| и |Ui2–| ограничены m;
· в лучшем О(n2) при n > m и О(m2) при m > n, если|Ui1+|, |Ui2+|, |Ui1–| и |Ui2–| ограничены константой.
Объектами операции могут быть два куска или кусок и подграф ультраграфа или гиперграфа.
При пересечении кусков ультраграфа HU1к (X1к, U1к) и HU2к (X2к, U2к) результатом будет подграф, если U1кext Ç U2кext = Æ и выполняется условие (16), в котором Xj1+ = Г2uj Î Г2U1к, Xj2+ = Г2uj Î Г2U2к, Xj1– = Г1uj Î Г1U1к и
Xj2– = Г1uj Î Г1U2к. В противном случае результатом будет кусок ультраграфа, у которого
Uкint = {uj Î Uк : Xj1+ = Xj2+ & Xj1– = Xj2– & uj Ï U1кext & uj Ï U2кext} и
Uкext = Uк \ Uкint.
При пересечении куска HU1к (X1к, U1к) и подграфа HU2 (X2, U2) ультраграфа результатом будет подграф, если U1кext Ç U2 = Æ и выполняется условие (16), в котором Xj1+ = Г2uj Î Г2U1к, Xj2+ = Г2uj Î Г2U2, Xj1– = Г1uj Î Г1U1к и Xj2– = Г1uj Î Г1U2. В противном случае результатом будет кусок ультраграфа, у которого
Uкint = {uj Î Uк : uj Ï U1кext & Xj1+ = Xj2+ & Xj1– = Xj2–} и
Uкext = Uк \ Uкint.
Автор надеется, что читатель сможет самостоятельно распространить эти выкладки на соответсвующие части гиперграфа.
Пример. Определим совпадающие части двух схем, изображенных на рис. 16, а. При представлении схем ультраграфами HU1 и HU2, показанными на рис.16, б, результатом операции HU1 (X1, U1) Ç HU2 (X2, U2) будет кусок ультраграфа HUк, так как в HU1 образ ребра u2 – Г2u2 = {x3, x4}, а в HU2 –
Г2u2 = {x3, x4, x5}. Используя приведенные выше формулы, получим следующие множества аналитического представления куска ультраграфа HUк:
Xк = {x1, x2, x3, x4} Ç {x1, x2, . ., x5} = {x1, x2, . . ., x4};
Uк = {u1, u2, u3} Ç {u1, u2, u4} = {u1, u2}, Uк int = {u1}, Uкext = {u2};
Г1Xк : Г1x1 = {u1, u2} Ç {u1, u2} = {u1, u2}, Г1x2 = {u3} Ç {u4} = Æ,
Г1x3 = { u3} Ç Æ = Æ, Г1x4 = Æ;
Г2Xк : Г2x1 = Æ, Г2x2 = {u1} Ç {u1} = {u1}, Г1x3 = {u1, u2} Ç {u1, u2} = {u1, u2}, Г1x4 ={u2, u3} Ç {u2, u4} = {u2};
Г2Uк : Г2u1 = {x2, x3} Ç {x2, x3} = {x2, x3}, Г2u1 = {x3, x4} Ç {x3, x4, x5} = {x3, x4};
Г1Uк : Г1u1 = { x1} Ç {x1} = {x1}, Г2u2 = { x1} Ç {x1} = {x1};
F1Xк : так как U1п+ = {u1, u2}, то F1x1 = {{x2, x3} Ç {x2, x3} È {x3, x4} Ç {x3, x4, x5}} = {x3, x4}, так как U2п+ = U3п+ = U4п+ = Æ, то F1x2 = F1x3 = F1x4 = Æ;
F1-1X к : так как U1п– = Æ, то F1-1x1 = Æ, U2п– = {u1} – F1-1x2 = {{x1} Ç {x1}} = {x1}, U3п– = {u1, u2} – F1-1x3 = {{x1} Ç {x1} È {x1} Ç {x1}} = {x1}, U4п– = {u2} – F1-1x4 = {{x1} Ç {x1}} = {x1};
F2Uк : так как X1п+ = {x2, x3}, то F2u1 = {{u3} Ç {u4} È {u3} Ç Æ} = Æ,
X2п+ = {x3, x4} – F2u2 = {{u3} Ç Æ È Æ Ç Æ} = Æ;
F2-1Uк : X1п– = X2п– = {x1} и F2-1u1 = F2-1u2 = Æ.
При описании операций были рассмотрены только два варианта аналитического представления ультра- и гиперграфов: полное и в некоторых примерах неполное – без образов (и прообразов для ультраграфов) вершин и рёбер относительно предикатов смежности. При решении задач структурного синтеза нередко возникает необходимость в получении других видов неполного представления графов, содержащих существенно меньший объем информации по сравнению с полным представлением. Анализируя выражения, приведенные в описаниях выполнения операций, нетрудно сформулировать обозначение операции для других вариантов неполного представления и определить используемые формализмы.
Рассмотрим в качестве примера операцию объединения частей графа. Пусть результатом операции объединения двух кусков ультраграфа HU1к и HU2к является ультраграф, который необходимо получить в виде HU (X, F1X). В результате анализа содержательно-формального описания операции
HU (X, U) = HU1к (X1к, U1к) È HU2 (X2к, U2к) нетрудно определить, что в качестве исходных данных необходимо задать для куска HU1к множества X1к, U1кext, Г1X1к, F1X1к и аналогичные множества для куска HU2к. Для получения результата в виде HU (X, F1X) достаточно выполнить преобразования, описанные в п. п. 1 и 6. Обозначение результата операции должно иметь вид:
HU (X, F1X) = HU1к (X1к, U1кext, Г1X1к, F1X1к) È HU2 (X2к, U2кext, Г1X2к, F1X2к).
Рассмотренные операции применимы к обыкновенным ориентированным и неориентированным графам. Особенности выполнения операций над такими графами связаны с тем, что их ребра инцидентны не более чем двум вершинам , что определяется истинностью условия – " uj Î U (|Г1uj| = |Г2uj| = 1 для графа G®(X, U) и – " uj Î U |Г2uj| = 2, если uj не является петлей, и |Г2uj| = 1 в противном случае для графа G~(X, U). Выражения, описывающие результат выполнения операций над обыкновенными графами, могут быть получены из формул для ультра- и гиперграфов, используя аналитику, приведенную в [1].
Литература
1. Овчинников В.А. Математические модели объектов задач структурного синтеза: Наука и образование. Инженерное образование: Эл. науч. издание. – 2009. – ╧ 4.
2. Овчинников В.А. Операции над ультра- и гиперграфами: Наука и образование. Инженерное образование: Эл. науч. издание. – 2009 – ╧ 10-11.
Публикации с ключевыми словами: структурный синтез, математические модели
Публикации со словами: структурный синтез, математические модели
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



