научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2008
УДК 621.98.073
Тульский государственный университет
Кафедра механики пластического формоизменения им. Н. Демидова
Научный руководитель: д.т.н., проф. Панфилов Г.В.
Разработана и внедрена в производство технология двухпереходной холодной штамповки специальных сферических шайб с высотой, превышающей высоту листовой заготовки, для монтажа волнообразных криволинейных секций металлических водоотводных труб. Спроектирован двухпозиционный двухрядный штамп с автоматической подачей полосы для реализации предлагаемой технологии. Для изготовления сферической шайбы был разработан двухпереходный технологический процесс, при котором на первом переходе необходимо сформировать сферическую и плоскую торцевые поверхности шайбы и осуществить пробивку отверстия. Одной из задач данного перехода является необходимость увеличения высоты шайбы по сравнению с толщиной полосы, из которой она изготавливается. На втором переходе предусматривается вырубка сферической шайбы.
Материал шайбы – марганцовая низколегированная конструкционная сталь 09Г2 (ГОСТ 17066-94). Механические характеристики данного материала приведены в таблице 1.
Таблица 1
|
Наименование механической характеристики |
Обозначение |
Единица измерения |
Величина |
|
Предел текучести |
σТ |
МПа |
320 |
|
Предел прочности |
σВ |
МПа |
470 |
|
Модуль упругости |
Е |
МПа |
2•105 |
|
Относительное удлинение |
δ |
% |
43 |
В качестве исследуемых выходных параметров, удовлетворяющих таким требованиям, как статистическая эффективность, возможность их количественной оценки и чувствительность к изменению факторов, примем ширину b кольцевой торцовой плоскости (y1) и степень заполнения q сферической торцовой поверхности (y2). Степень заполнения материалом сферической торцовой поверхности полуфабриката первого перехода оценивалась по соотношению площади полуфабриката, вступившей в контакт с рабочей полостью матрицы, к общей площади этой сферической полости матрицы. Оценка (в процентах) производилась по отпечаткам следов контактной поверхности на сферическом участке полуфабриката предварительного перехода. Геометрические параметры шайбы, принятые в качестве выходных параметров, показаны на рис. 1.
Варьируемыми факторами в данном экспериментальном исследовании [1,2] являлись: угол φ конусности заостренной части пробивного пуансона (X1) и глубина h вдавливания в полосу плоского пуансона (совмещенного с пробивным) предварительного перехода (X2), формующего кольцевой плоский торец и перераспределяющего деформируемый материал в сферический участок полуфабриката шайбы.


Рис. 1. Принятые выходные параметры: y1 – ширина кольцевой торцовой плоскости; y2 - степень заполнения сферической торцовой поверхности
Пробивные пуансоны, используемые в данном многофакторном эксперименте с различными углами конусности заостренного участка, соответствующими различным уровням фактора X1, приведены на рис. 2.

Рис. 2. Варианты пробивных пуансонов, соответствующие различным уровням фактора X1
Принятые значения факторного пространства приведены в таблице 2.
Таблица 2
|
Обозначение Фактора |
Наименование фактора |
Размерность
|
Область эксперимента |
|||
|
Нижний уровень
|
Основной уровень
|
Верхний уровень
|
Интервал варьирования |
|||
|
X1 |
Полный угол конусности заостренной части пробивного пуансона |
градус |
60 |
90 |
120 |
30 |
|
X2 |
Глубина вдавливания плоскости пуансона в полосу |
мм |
0,5 |
1,0 |
1,5 |
0,5 |
В соответствии с критериями геометрического подобия при планировании и проведении многофакторных исследований предпочтительно использование безразмерных величин факторов и соответствующих им выходных параметров, поэтому, согласно практике моделирования процессов пластической деформации, толщина s изготавливаемой шайбы (исходной полосы) являлась масштабным фактором.
Варьирование каждого фактора производилось на трех уровнях. Уровни факторов ![]() представим в кодовом масштабе
представим в кодовом масштабе ![]() значениями 0, 1, 2. В планы входит фиктивная переменная
значениями 0, 1, 2. В планы входит фиктивная переменная ![]() , необходимая для расчета свободного члена регрессии и имеющая во всех опытах уровень
, необходимая для расчета свободного члена регрессии и имеющая во всех опытах уровень ![]() . Запись матрицы планирования полного факторного эксперимента
. Запись матрицы планирования полного факторного эксперимента ![]() приведена в таблице 3.
приведена в таблице 3.
Таблица 3.
|
╧ опыта |
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
0 |
1 |
0 |
1 |
2 |
0 |
|
3 |
0 |
2 |
0 |
2 |
1 |
0 |
|
4 |
0 |
0 |
1 |
1 |
0 |
2 |
|
5 |
0 |
1 |
1 |
2 |
2 |
2 |
|
6 |
0 |
2 |
1 |
0 |
1 |
2 |
|
7 |
0 |
0 |
2 |
2 |
0 |
1 |
|
8 |
0 |
1 |
2 |
0 |
2 |
1 |
|
9 |
0 |
2 |
2 |
1 |
1 |
1 |
Значения уровней для эффектов взаимодействий определены сложением уровней взаимодействующих факторов и делением суммы на число уровней варьирования факторов в эксперименте. Остаток от деления дает значения уровня. Приведенный выше кодированный масштаб применяется при составлении планов, а для обработки данных эксперимента применяют другой кодированный масштаб.
Искомую математическую модель исследуемого процесса аппроксимируем следующим полиномом
y = b0 + b1X1 + b2X2 + b12X1X2 + b11X12 + b22X22 (1)
![]() - факторы в натуральном масштабе, т.е. в МПа, м, кг и т.д.
- факторы в натуральном масштабе, т.е. в МПа, м, кг и т.д.
В кодированном масштабе модель представим в виде:
y = b0 + b1x1 + b2x2 + b12x1x2 + b11z1 + b22z2, (2)
где ![]() - линейная функция от
- линейная функция от ![]() ;
; ![]() - квадратичная функция от
- квадратичная функция от ![]() .
.
Приведем зависимости, необходимые для перехода от натуральных значений факторов к кодированным [3,4].
Запишем линейную функцию от ![]() в виде
в виде
![]() , (3)
, (3)
где ![]() и
и ![]() - константы.
- константы.
 . (4)
. (4)
После подсчёта ![]() коэффициенты
коэффициенты ![]() подбираем таким образом, чтобы уровни
подбираем таким образом, чтобы уровни ![]() представляли собой небольшие целые числа.
представляли собой небольшие целые числа.
Далее запишем ![]() , как квадратичную функцию от
, как квадратичную функцию от ![]() ,
,
![]() , (5)
, (5)
где ![]() ,
, ![]() ,
, ![]() - константы.
- константы.
 ;
; 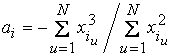 . (6)
. (6)
Коэффициенты ![]() выбираем из условия, чтобы уровни
выбираем из условия, чтобы уровни ![]() представляли собой небольшие целые числа.
представляли собой небольшие целые числа.
Расчет средних значений выходных параметров для каждой комбинации факторов (строки в матрице планирования) и построчных дисперсий по результатам параллельных опытов проведем по формулам
 ;
; 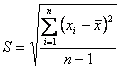 . (7)
. (7)
Для расчета кодированных значений факторов с помощью принятых численных натуральных значений их уровней и таблицы 3 приведем столбцы матрицы планирования, определяющие комбинации факторов (условия проведения) для каждого опыта (таблица 4).
Таблица 4
|
Номер опыта |
|
|
Порядок реализации |
Номер опыта |
|
|
Порядок реализации |
|
1 |
60 |
0,5 |
3 |
6 |
120 |
1,0 |
9 |
|
2 |
90 |
0,5 |
7 |
7 |
60 |
1,5 |
5 |
|
3 |
120 |
0,5 |
2 |
8 |
90 |
1,5 |
6 |
|
4 |
60 |
1,0 |
8 |
9 |
120 |
1,5 |
4 |
|
5 |
90 |
1,0 |
1 |
|
|
|
|
По формуле (4) определим константу ![]() , входящую в зависимость (3):
, входящую в зависимость (3):
![]() ;
; ![]() .
.
Подберем коэффициенты ![]() :
: ![]() ;
; ![]() .
.
С учетом полученных значений зависимость (3) принимает вид
![]() ;
; ![]() (8)
(8)
Зависимость (8) позволяет найти кодированные значения уровней, которые для обоих факторов в данном конкретном случае будут одинаковыми: нижний уровень ![]() ; основной (нулевой) уровень
; основной (нулевой) уровень ![]() ; верхний уровень
; верхний уровень ![]() .
.
По формуле (6) определим константы ![]() и
и ![]() , входящие в зависимость (5):
, входящие в зависимость (5):
![]() ;
; ![]() .
.
Подберем коэффициенты ![]() :
: ![]() =
=![]() =3.
=3.
С учетом полученных значений зависимость (5) принимает вид
![]() (9)
(9)
Зависимость (9) позволяет найти кодированные значения уровней ![]() , как квадратичной функции от кодированных значений факторов
, как квадратичной функции от кодированных значений факторов ![]() , которые для обоих факторов в данном конкретном случае будут одинаковыми: нижний уровень
, которые для обоих факторов в данном конкретном случае будут одинаковыми: нижний уровень ![]() ; основной (нулевой) уровень
; основной (нулевой) уровень ![]() ; верхний уровень
; верхний уровень ![]() .
.
Таким образом, совершен переход к кодированному масштабу, в котором план эксперимента симметричен и ортогонален.
План эксперимента в кодированном масштабе представлен в таблице 5.
Таблица 5
|
╧ опыта
|
Варьируемые факторы
|
Выходные параметры |
||||||||||||||
|
|
|
|
|
|
|
y1 |
y2 |
|||||||||
|
y11 |
y12 |
y13 |
|
|
y21 |
y22 |
y23 |
|
|
|||||||
|
1 |
1 |
-1 |
-1 |
1 |
1 |
1 |
3,1 |
3.1 |
3,4 |
3,2 |
0.173 |
61 |
61 |
64 |
62 |
1,73 |
|
2 |
1 |
0 |
-1 |
-2 |
1 |
0 |
1,9 |
2,0 |
2,1 |
2,0 |
0,1 |
44 |
45 |
43 |
44 |
1,0 |
|
3 |
1 |
1 |
-1 |
1 |
1 |
-1 |
2.6 |
2,5 |
2,5 |
2,4 |
0,173 |
53 |
53 |
53 |
53 |
0 |
|
4 |
1 |
-1 |
0 |
1 |
-2 |
0 |
4,6 |
4,6 |
4,6 |
4,6 |
0 |
82 |
79 |
82 |
81 |
1,73 |
|
5 |
1 |
0 |
0 |
-2 |
-2 |
0 |
3,2 |
3,2 |
3,5 |
3,3 |
0,173 |
64 |
66 |
66 |
65 |
1,73 |
|
6 |
1 |
1 |
0 |
1 |
-2 |
0 |
4,0 |
3,6 |
3,5 |
3,7 |
0,265 |
71 |
75 |
76 |
74 |
2,65 |
|
7 |
1 |
-1 |
1 |
1 |
1 |
-1 |
5,9 |
6,0 |
6,1 |
6,0 |
0,1 |
101 |
101 |
101 |
101 |
0 |
|
8 |
1 |
0 |
1 |
-2 |
1 |
0 |
4,9 |
4,5 |
4,4 |
4,6 |
0,265 |
84 |
85 |
86 |
85 |
1,0 |
|
9 |
1 |
1 |
1 |
1 |
1 |
1 |
4,9 |
5,2 |
5,2 |
5,1 |
0,173 |
93 |
96 |
96 |
95 |
1,73 |
Для проведения экспериментальных исследований был использован однорядный двухпозиционный штамп, конструкция и работа которого описаны в разделе 3. Он спроектирован для завершающей экспериментальной отработки технологических процессов и рабочего инструмента, а также для изготовления мелких партий сферических шайб. Фотографии штампа представлены на рис. 6.

Рис. 6. Однорядный двухпозиционный штамп, используемый для проведения экспериментальных исследований
Экспериментальные исследования проводились на предприятии ОАО «Алексинстройконструкция» с использованием механического пресса модели КД2126Е. Скоростной параметр деформирования этого пресса (140 ходов в минуту) соответствует скорости перемещения ползуна основного прессового оборудования, на котором изготавливают сферические шайбы. Технологическая сила – 400кН, регулировка хода ползуна – 70 мм. Для повышения достоверности результатов при одной и той же комбинации факторов проводилось три параллельных опыта, порядок реализации опытов выбран по таблице случайных чисел. Штамповая оснастка и рабочий инструмент первого перехода приведены на рис. 7, а второго перехода –
на рис. 8.


Рис. 7. Штамповая оснастка Рис. 8. Штамповая оснастка
и инструмент первого перехода и инструмент второго перехода
При реализации экспериментов с минимальным углом конусности
![]() = 600 заостренной части пробивного пуансона (рис. 9) на первом переходе наблюдается проколка с частичным разрушением отхода перед пробивкой отверстия. Это приводит к тому, что материал заготовки незначительно затягивается в полость матрицы перед пробивкой и, как следствие, при наиболее благоприятных условиях для качественного формообразования сферической поверхности и ширины кольцевой торцовой плоскости шайбы качество поверхности отверстия после пробивки – наихудшее. Текстурный анализ кольцевого шлифа со стороны сферической поверхности шайбы показал, что трещины частично проникают и в тело шайбы, что отрицательно скажется на прочности соединения при долговременном нахождении трубы в грунте.
= 600 заостренной части пробивного пуансона (рис. 9) на первом переходе наблюдается проколка с частичным разрушением отхода перед пробивкой отверстия. Это приводит к тому, что материал заготовки незначительно затягивается в полость матрицы перед пробивкой и, как следствие, при наиболее благоприятных условиях для качественного формообразования сферической поверхности и ширины кольцевой торцовой плоскости шайбы качество поверхности отверстия после пробивки – наихудшее. Текстурный анализ кольцевого шлифа со стороны сферической поверхности шайбы показал, что трещины частично проникают и в тело шайбы, что отрицательно скажется на прочности соединения при долговременном нахождении трубы в грунте.

Рис. 9. Отштампованная шайба и отход пробивки отверстия при минимальном угле конусности ![]() = 600 заостренной части пробивного пуансона
= 600 заостренной части пробивного пуансона
На рис. 10 показано сквозное проникновение трещин в материал отхода после пробивки, что также подтверждает их продолжение в тело шайбы.

Рис. 10. Характер проникновения макротрещин
в материал отхода
Использование пуансонов с углом конусности ![]() = 900 (рис. 11) обусловливает близкое к максимальному уменьшение ширины плоского торцового кольца и ухудшение качества заполнения сферической поверхности шайбы. При этом качество поверхности пробитого отверстия значительно повышается.
= 900 (рис. 11) обусловливает близкое к максимальному уменьшение ширины плоского торцового кольца и ухудшение качества заполнения сферической поверхности шайбы. При этом качество поверхности пробитого отверстия значительно повышается.
Как видно из рис.11, при данном угле конусности пробивного пуансона проколки отхода не наблюдается, а происходит лишь образование макротрещины.

Рис. 11. Отштампованная шайба и отход пробивки отверстия при угле
конусности ![]() = 900 заостренной части пробивного пуансона
= 900 заостренной части пробивного пуансона
Пробивные пуансоны с наибольшим значением угла конусности
(рис.12) обеспечивают по сравнению с предыдущим вариантом комбинации факторов увеличение качества заполнения материалом сферической поверхности шайбы, сопровождающееся соответствующим увеличением ширины плоского торцового кольца.

Рис. 12. Отштампованная шайба и отход пробивки отверстия при максимальном угле конусности ![]() = 1200 заостренной части пробивного пуансона
= 1200 заостренной части пробивного пуансона
Очевидно, что увеличение глубины вдавливания в полосу плоского торца пуансона первого перехода однозначно приводит к увеличению плоского торцового кольца шайбы и качества заполнения ее сферической поверхности, а также к уменьшению общей высоты шайбы.
Поскольку при переходе к кодированному масштабу условия симметричности и ортогональности плана эксперимента были соблюдены, коэффициенты регрессии модели (2) рассчитываем по формуле
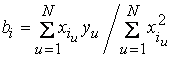 , (10)
, (10)
где ![]() - номер фактора.
- номер фактора.
При подсчете дисперсии выходного параметра квадрат разности между значениями ![]() и средним значением из n повторных наблюдений
и средним значением из n повторных наблюдений ![]() (7) нужно просуммировать по числу опытов в матрице планирования N, а затем разделить на N (n-1)
(7) нужно просуммировать по числу опытов в матрице планирования N, а затем разделить на N (n-1)
 . (11)
. (11)
Формулой (11) можно пользоваться лишь в случае, если все построчные дисперсии однородны, т.е. среди них нет таких, которые бы значительно превышали остальные. Поскольку во всех точках плана число повторных опытов одинаково, для проверки однородности дисперсий воспользуемся критерием Кохрана [5]. Проверку значимости коэффициентов регрессии проведем с помощью критерия Стъюдента.
После расчета коэффициентов регрессии уравнение модели (2) принимает вид
y1 = 3,88 – 0,43x1 + 1,35x2 – 0,0025x1x2 + 0,29z1 + 0,0055z2,
а после проверки значимости коэффициентов регрессии:
y1 = 3,88 – 0,43x1 + 1,35x2 + 0,29z1 . (15)
y2 = 73,22 – 3,5x1 + 20,5x2 + 0,5x1x2 + 4,28z1 – 0,78z2,
а после проверки значимости коэффициентов регрессии:
y2 = 73,22 – 3,5x1 + 20,5x2 + 0,5x1x2 + 4,28z1. (3.16)
Далее проводим проверку адекватности (точности) полученных уравнений регрессии (моделей), которая состоит в выяснении соотношения между дисперсией адекватности Sад2 и дисперсией воспроизводимости Sy2 c помощью F-критерия Фишера.
Полученные уравнения (15) и (16) записаны в кодированном масштабе и неудобны для практического использования. Для перевода их в натуральный масштаб используем уравнения (8) и (9). В начале члены, содержащие ![]() , раскрываем в форме функции от
, раскрываем в форме функции от ![]() , а затем все члены раскрываем в форме функции от
, а затем все члены раскрываем в форме функции от ![]() и
и ![]() . В процессе раскрытия выражений приводим подобные члены.
. В процессе раскрытия выражений приводим подобные члены.
Ширина кольцевой торцовой плоскости сферической шайбы определяется по уравнению
b = 9,72 – 0,1883φ + 2,7h + 0,00096 φ2, (19)
где φ - угол конусности заостренной части пробивного пуансона;
h - глубина вдавливания в полосу плоского пуансона. &nb sp;
Степень заполнения сферической торцовой поверхности шайбы (в процентах) определяется по уравнению
q = 154,22 – 2,7347φ + 38h + 0,03335 φ h + 0,01412 φ2 . (20)
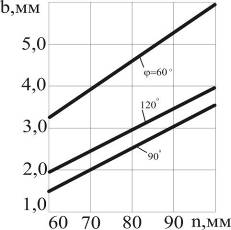
С помощью уравнения (19) построим графические зависимости ширины кольцевой торцовой плоскости от угла конусности заостренной части пробивного пуансона и глубины вдавливания в полосу плоского пуансона первого перехода, а с помощью уравнения (20) – графические зависимости качества заполнения сферической поверхности шайбы от этих же факторов.
|
|
|
|
Рис.13. Зависимость степени заполнения сферической поверхности шайбы от угла φ конусности пробивного пуансона для различный значений глубины h вдавливания плоского торца пуансона первого перехода. |
Рис.14. Зависимость степени заполнения сферической поверхности шайбы от глубины h вдавливания плоского торца пуансона первого перехода для различных значения угла φ конусности пробивного пуансона. |
|
|
|
|
Рис.15. Зависимость ширины кольцевой торцовой плоскости шайбы от угла φ конусности заостренной части пробивного пуансона для различных значений глубины h вдавливания плоского торца пуансона первого перехода. |
Рис.16. Зависимость ширины кольцевой торцовой плоскости шайбы от глубины вдавливания плоского торца пуансона первого перехода для различных значений угла φ конусности заостренной части пробивного пуансона. |
Анализ уравнений (19), (20) и полученных графических зависимостей, иллюстрирующих эти уравнения, показал, что для штамповки сферических шайб с размерами, указанными на рис.3.3, целесообразно использовать пробивной пуансон с углом конусности заостренной части 1200 и назначать глубину вдавливания в полосу плоского торца пуансона первого перехода, равную 1 мм.
Использование пробивных пуансонов с небольшими углами конусности, также обеспечивающих хорошее качество заполнения сферической поверхности шайбы и необходимую ширину кольцевой торцовой плоскости, нецелесообразно из-за неудовлетворительного качества поверхности пробитого отверстия и наличия трещин в получаемой шайбе.
Литература
1. Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. М.: «Наука», 1976. – 279с.
2. Финни Д. Введение в теорию планирования экспериментов. М.: «Наука», 1970. – 287 с.
3. Дмитриев А.М., Капустин А.И. Технология листовой штамповки. М.: «НПП – Темп»,1993. – 34 с.
4. Григорович В.Г., Кершенбаум В.Я., Козочкин Д.А., Шильдин В.В., Юдин С.В. Информационно-статистические методы в технологии машиностроения. Пособие по обработке результатов эксперимента. М.: «Нефть и газ»,2000. – 183с.
Публикации с ключевыми словами: штамповка, формообразование
Публикации со словами: штамповка, формообразование
Смотри также:
- Разработка оптимальной технологии штамповки детали ╚подвеска╩ с использованием системы моделирования QFORM
- Моделирование процесса штамповки диска из жаропрочного никелевого сплава ЭП 742-ИД
- Моделирование процесса обратного выдавливания деталей из сплаваБрБ2 по схеме подвижного контейнера с применением DEFORM-2D
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||