научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2013
DOI: 10.7463/1213.0640867
УДК 658.51
Россия, МГТУ им. Н.Э. Баумана
Введение
При проектировании технологических процессов механической обработки, вопрос выбора металлорежущих станков занимает одну из ключевых позиций. В этой связи, процедура выбора станков, как одного изсредств технологического оснащения производства, регламентирована стандартами Р 50-54-11-87 и РД 50-532-85, в которых сформулированы общие руководящие принципы выполнения этой процедуры. В то же время, технический аспект выбора станков в настоящее время, к сожалению, ещё не достаточно проработан в деталях. Поэтому, процесс выбора остаётся не формализованным, хотя, в соответствии с современной концепцией комплексной автоматизации инженерного проектирования [1, 2] ожидается, что эта проектная процедура должна выполняться с применением средств САПР ТП. Таким образом, современное состояние обсуждаемой проблемы требует разработки формализованного подхода к выбору станков, теоретические предпосылки для которого, как можно судить по результатам, полученным в работе [3], имеются. Тем не менее, поскольку содержание упомянутой выше работы ограничено рассмотрением аналитического аспекта проблемы, полученные в ней результаты, нуждаются в подтверждении результатами решения практической задачи. В связи с этим, целью настоящей работы является апробация практической применимости известных оптимизационных методов для решения практических задач выбора станка. В работе обсуждается общая постановка задачи, рассмотрено её решение с использованием современных методов многокритериального оптимизационного выбора; и выполнен анализ полученных результатов.
Основная часть
В настоящее время, при проектировании технологических процессов механической обработки применяется [4] двухэтапная процедура выбора станка (Рис. 1). На первом этапе, при маршрутной проработке технологических операций, из исходного семейства станков МС выделяется множество потенциально приемлемых альтернатив МА∈МС. Второй этап выполняется на стадиях детальной проработки технологической операции. На этом этапе из множества альтернатив МА выбирается одна наиболее привлекательная модель станка OPTmAk∈МА∈МС, которая и принимается (рис. 1), как рабочая альтернатива модели для данной операции.
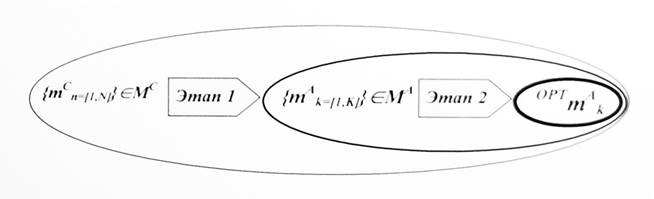
Рис. 1. Схема двухэтапного выбора модели станка.
Двухэтапный подход к процедуре выбора обусловлен объективной логикой общего развития технологических проектов [4] и утвердился в роли базового метода выбора моделей станков. Заметим, также, что на двухэтапную процедуру выбора станков хорошо проецируются современные методы многокритериального оптимизационного выбора. В связи со сказанным, в настоящей работе предпринята попытка практической реализации двухэтапного выбора модели станка, базирующегося на формализованных подходах. Выполнение этой задачи требует рассмотрения следующих вопросов:
I. Анализ исходных данных и формулирование ограничительных условий задачи.
II. Выявление множества потенциально приемлемых моделей станка.
III. Выбор предпочтительной модели станка.
I. Анализ исходных данных и формулирование ограничительных условий задачи
Рассмотрим задачу выбора модели станка в следующей конкретной постановке. Разрабатывается технологический процесс механической обработки детали типа «Вал быстроходный» (рис. 2). Деталь характеризуется хорошей технологичностью: удобными для изготовления габаритными размерами и массой, простой формой, хорошей обрабатываемостью материала, умеренными требованияи к точности и шероховатости обрабатываемых поверхностей (точность основных поверхностей по 6…8 квалитету, шероховатость ≤1,2 мкм). Заданный объём выпуска детали равный 1200 шт/г. при массе детали равной 4,9 кг относит проектируемый процесс к среднесерийному типу производства. [5].

Рис. 2. Эскиз детали «Вал быстроходный.
Для изготовления детали задан технологический маршрут, включающий девять операций: 1) отрезание заготовки (круговой прокат); 2) фрезерно-центровальная обработка торцов заготовки; 3) токарная обработка всех круговых и торцевых поверхностей вала; 4) фрезерная обработка шпоночных пазов; 5) термическая обработка (цементация, закалка, отпуск); 6) шлифование шеек вала (диаметр 50 и 45); 7) слесарная обработка (калибровка резьбы); 8) моечная очистка детали; 9) выходной контроль детали. Основной и наиболее трудоёмкой операцией технологического процесса является токарная обработка вала.
Требуется выбрать предпочтительную модель токарного станка из числа станков, имеющихся в станочном парке цеха-изготовителя и приведённых в таблице 1.
Таблица 1
Базовые технологических характеристик металлорежущих станков с ЧПУ токарной группы
№ п/п | Параметры станка (технологический аспект) | Модель станка | |||
16А20Ф3 | 16М30Ф3 | ТПК125АФ4 | РТ777Ф3 | ||
1. | Класс точности станка | Н | Н | А | Н |
2. | Тип СУ | Контурная | Контурная | Контурная | Контурная |
3. | Схема установки детали | ПтЦн | ПтЦн | Пт | ПтЦн** |
4. | Тип накопителя инструментов | РГ | РГ | РГ | РГ |
5. | Тип опорной поверхности станины | Горизонтальная | Горизонтальная | Наклонная | Наклонная |
6. | Макс. габариты заготовки (D х L), мм | 200 х 1000 | 320 х 1000 | 100 х 180 | 400х600 |
7. | Макс. масса заготовки, кг | 25 | 60 | 15 | 80 |
8. | Частота вращения шпинделя, об/мин | 20 … 2500 | 8 … 2000 | 50 … 4000 | 10 … 3150 |
9. | Мощность привода, кВт | 11 | 30 | 4 | 45 |
10. | Величины подач ( Sz), мм/мин | 1 … 1000 | 1 … 4000 | 1 … 6000 | 1 … 4000 |
11. | Погрешности позиционирования, мм | ± 0,010 | ± 0,007 | ± 0,002 | ± 0,008 |
12. | Ёмкость накопителя инстр-тов, шт | 6, 8, 12 | 4 | 6 | 12 |
13. | Габариты станка (ДхШхВ), мм | 3200х2200х1600 | 5500х 3600 х 2130 | 1680 х 1040 х1630 | 4500х2750х2470 |
14. | Масса станка, кг | 4000 | 16000 | 1850 | 9000 |
ПтЦн – патронно-центровая; Пт – патронная; РГ – револьверная головка
В заданном технологическом процессе операция токарной обработки выполняется за два установа. При этом применяются следующие технологические переходы: подрезание торца (подрезной резец), продольное точение и снятие фасок (проходной упорный резец), прорезание канавки (канавочный резец) и нарезание резьбы (резьбовой резец). Для выполнения токарной обработки назначены режимы, имеющие следующие значения технологических параметров: частота вращения шпинделя – 127…1460 об/мин; продольная подача – 0,14…0,70 мм/об; поперечная подача – 0,05…0,18 мм/об. Обработка на заданных режимах требует, чтобы мощность привода шпинделя была не ниже 4,1 кВт.
Заданные условия изготовления детали «вал быстроходный» накладывают на токарный станок технологические ограниченияPТ ={pТj=[1,J] }, приведённые в таблице 2.
Таблица 2
Технологические ограничения на параметры токарного станка-претендента
Набор технологических ограничительных параметров PТ ={pТj=[1,J] } |
Допустимые значения параметров | |
ОбозначениеpТj | Наименование параметра | |
pТ1 | Тип станка | Токарный, патронно-центровой с ЧПУ |
pТ2 | Тип системы управления | Контурная, Ф3 или Ф4 |
pТ3 | Класс точности | Н (или П или В или А) |
pТ4.1 pТ4.2 | Габариты обрабатываемой заготовки, мм
| Диаметр не менее70 Длина не менее 350 . |
pТ5 | Масса обрабатываемой заготовки, кг | Не менее5 кг |
pТ6.1 pТ6.2 | Диапазон частоты вращения шпинделя, об/мин | Нижняя граница не более127 Верхняя граница не менее1460. |
pТ7 | Мощность привода шпинделя, кВт | Не менее 4,1 |
pТ8.1 pТ8.2 | Диапазон регулирования продольной подачи, мм/об | Нижняя граница не более0,14 Верхняя граница не менее 0,70 |
pТ9.1 pТ9.2 | Диапазон регулирования поперечной подачи, мм/об | Нижняя граница не более 0,05 Верхняя граница не менее 0,18 |
pТ10 | Ёмкость оперативного накопителя инструментов | Не менее6 позиций. |
Параметры PТ, задающие технологические ограничения рассматриваемой задачи, являются тем набором данных, которые позволяют выделить из исходного семейства станков МС множества МА, которое являются альтернативным набором моделей, потенциально приемлемых для выполнения проектируемой технологической операции.
II. Выявление множества потенциально приемлемых моделей станка
Для рассматриваемой нами конкретной задачи, модели исходного семейства станков {mСn=[1,N]}∈МС, в рамках которого должны быть выявлены потенциально приемлемые альтернативны моделей {mАk=[1,K]}∈МА, приведены в таблице 1.
Анализ исходного семейства станков МС для выявления множества потенциально приемлемых моделей МА, осуществляется сопоставлением технологических параметров {pТj=[1,J]}∈РT, задающих ограничительные условия проектируемой операции, с одноимёнными параметрами {pСi=[1,I]}n=[1,N]∈PСn каждой из моделей, входящих в исходное семейство МС. Процедура такого сопоставления заключается (1) в проверке справедливости отношений «≥», «≤» или «=», задающих условия приемлемости каждой n-ной модели mСn=[1,N]по каждому из её параметров pСin. в паре с одноимённым ограничительным параметром pTj,:

где: [pT_maxj] – предельное значение числового параметра, задающего технологические ограничения «сверху» (в табл.2 это pТ4, 5, 6.2, 7, 8.2, 9.2, 10); [pT_maxj] - предельное значение числового параметра, задающего технологические ограничения «снизу» (в табл.2 - pТ6.1, 8.1, 9.1,); [pT_nomj] – номинальное значение вербального параметра, задающего технологическое ограничение условием «равнозначности» (в табл.2 - pТ1, 2, 3,); j=[1,J] - текущий номер параметра pTjв списке технологических ограничений РТ; pCin - значение i–того параметра n-ной модели станка, входящего в состав исходного семейства МС; n=[1,N] - текущий номер модели mСn станка в исходном семействе станков МС; {mАk=[1,K]}∈МА - множество потенциально приемлемых альтернативных моделей станка.
Процедура сопоставления каждой единичной пары (pСin, pTj) может иметь один из двух исходов: «выполнение» или «невыполнение» заданного отношения xor{≥,≤,=}. В зависимости от исходов по совокупности процедур i=[1,I] решается вопрос о включении каждой n–ной модели mСn=[1,N]. семейства МС в искомое множество МА (2):
![]()
Рассмотренная процедура может быть программно реализована на алгоритме, использующем продукционные правила (булевы конструкции «ЕСЛИ, … ТО…»), реализуемые (рис. 3), например, на операторах условного перехода типа «If … Then … Else».

Рис. 3. Алгоритм выявления потенциально приемлемых альтернативных моделей станка.
В случае выявления потенциально приемлемых альтернативных моделей станка в неавтоматизированном «ручном» варианте, при котором часть формализованных логических действий алгоритма (рис. 3) выполняется «в уме», процедура выявления множества МА можно регистрировать, используя «карту соответствия» моделей исходного семейства МС требованиям технологических ограничений РТ проектируемой операции.
В рассматриваемом нами примере, содержание «карты соответствия» (табл. 3) показывает, что из числа моделей, имеющихся в станочном парке цеха-изготовителя, для токарной обработки детали «Вал быстроходный» могут быть применены станки моделей 16А20ПФ3 и РТ777Ф3.
Таблица 3.
Карта соответствия станков-претендентов требованиям технологических ограничений
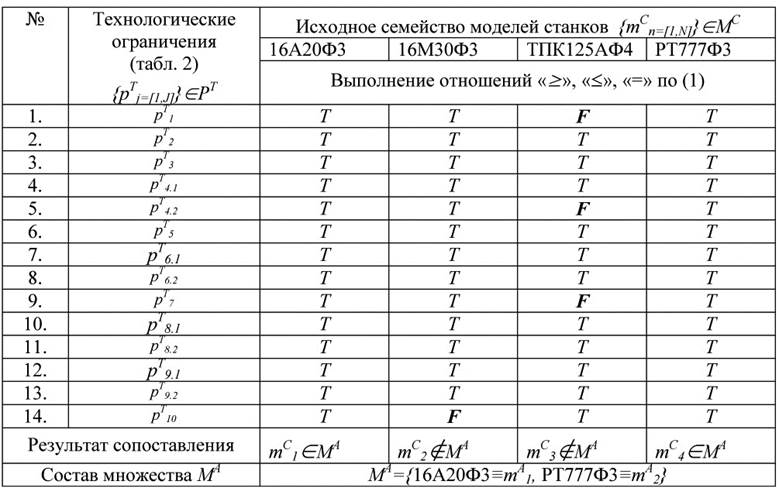
Таким образом, формально заданный перечень ограничительных условий, налагаемых условиями механической обработки детали, позволяет формализовать процедуру выявления множества потенциально приемлемых станков, претендующих на роль оптимального исполнителя проектируемой технологической операции.
III. Выбор предпочтительной модели станка
Процесс выбора предпочтительной модели станка базируется на двух аксиоматических допущениях: 1) искомая предпочтительная модель станка OPTmAk, является элементом множества потенциально приемлемых альтернатив МА={mАk=[1,K]} и выбирается из этого множества; 2) степень предпочтительности альтернатив mАk=[1,K] определяется совокупностью значений параметров PCn={pCi=[1,I]}n=[1,N], характеризующих технологический потенциал каждой рассматриваемой модели mАk=[1,K]. В этой связи, определение предпочтительной модели станка может быть сведено к задаче многокритериального оптимизационного выбора, в которой роль критериев оптимизации играет множество технологических параметров станкаPCn={pCi=[1,I]}n=[1,N], а решением задачи является идентификация оптимальной модели OPTmAk, в множестве МА={mАk=[1,K]}.
Отличительной особенностью решения такой оптимизационной задачи является то, что оцениваемые в ней критерии оптимизации характеризуются высокой метрологической неоднородностью. Они принадлежат к различным видам измерительных шкал; имеют числовое и нечисловое измерение, обладают различной физической природой, измеряются в существенно отличающихся диапазонах возможных числовых значений и характеризуются противоречивыми квалиметрическими трендами. В связи с этим, процедуре выбора оптимальной альтернативы OPTmAkдолжно предшествовать преобразование параметров станка PCn={pCi=[1,I]}n=[1,N], приводящее их к единой измерительной природе и к единому измерительному масштабу. В роли инструмента для такого преобразования может быть использована процедура нормализации переменных, которая позволяет описать каждую оцениваемую альтернативу mAkвектором метрологически однородных критериев {qi=[1,I]}k=[1,K], множество которых затем может быть свёрнуто в обобщённый скалярный показатель предпочтительности.
В свете сказанного, выполнение стадии «Выбор предпочтительной модели станка» предполагает решение следующих вопросов:
III.1. Нормализация параметров станка.
III.2. Многокритериальное описание функции предпочтительности станка.
III.3. Выбор оптимальной модели станка.
III.1. Нормализация параметров станка
Для нормализации числовых параметров станка удобно применить [6] дробно-линейную функцию (4):

где: +pСi - i–тый нормируемый параметр с повышающим трендом; -pСi - i–тый нормируемый параметр с понижающим трендом; pСi- числовое значение нормализуемого i–того параметра станка в множестве PC={pCi=[1,I]}; pСimin - минимальное значение нормализуемого i-того параметра; pСimax - максимальное значение нормализуемого i-того параметра; qi – нормализованное значение i–того параметра.
Нормализации вербальных параметров станка может быть выполнена с применением вербально-числовой шкалы биэкспоненциальной функции полезности [7], которая связывает вербальную оценку измеряемой «полезности» с эквивалентной нормализованной числовой оценкой «полезности» этого же параметра (табл. 4).
Таблица 4. Вербально-числовая шкала функции «полезности»
| |||||||||||||||||||||||
Таким образом, в результате преобразования исходных параметрических описаний РCk={pCi=[1,I]}k=[1,K] конкурирующих моделей станка, для каждой модели {mAk=[1,K]} станка может быть получено нормализованное параметрическое описание Qk={qi=[1,I]}k=[1,K]. При этом, нормализованные величины qiв каждом k-том нормализованном множестве Qkсохранят пропорции «полезности», эквивалентные пропорциям «полезности» параметров pCiв соответствующем k-том исходном множестве РCk. Поэтому, нормализованные множества Qk, являются состоятельными эквивалентами множеств РCk и могут быть применены для решения задачи сравнительного анализа привлекательности альтернативных моделей mAk. множества МА потенциально приемлемых моделей металлорежущих станков.
В рассматриваемой нами демонстрационной задаче, нормализация параметрического описания сравниваемых моделей станков сводится к преобразованию исходных параметрических описаний двух моделей: МА={16А20Ф3≡mА1, и РТ777Ф3≡mА2}. Отметим, что первые пять параметров исходного параметрического описания РСkэтих станковимеют нечисловую природу и их нормализация выполняется здесь с применением вербально-числовой шкалы полезности (табл. 4). Остальные параметры имеют числовое измерение и нормализуются с использованием кусочно-линейной функции (4). Следует также учесть, что параметры +p[7,12] и +pС14 имеют повышающий квалиметрический тренд, а параметры -pС13 и -pС[15, 18] характеризуются понижающим трендом. После нормализации исходных параметрических описаний станков модели 16А20Ф3 и РТ777Ф3, мыполучим параметрические множества Qk={qi=[1,I=18]}k=[1,K=2] (табл. 5), которые на последующих этапах решения задачи III будут выступать в роли оптимизационных критериев выбора предпочтительной модели OPTmАkстанка (табл. 5), рекомендуемого для выполнения токарной обработки детали «Вал быстроходный».
Таблица 5
Нормализация параметрического описание сравниваемых станков
Наименование параметров | Значения параметров | ||||||
У класса станков* | У станка 16А20Ф3≡mА1 | У станка РТ777Ф3≡mА2 | |||||
pi min | pi max | pСi 1 | qi 1 | pСi 2 | qi 2 | ||
Класс точности | +pС 1 | Н | А | Н | 0,40 | Н | 0,40 |
Тип системы управления | +pС2 | Ф1 | Ф4 | Ф3 | 0,50 | Ф3 | 0,50 |
Схема установки детали | +pС3 | Пт | ПтЦн | ПтЦн | 0,50 | ПпЦн | 0,50 |
Тип накопителя инструментов | +pС4 | РГ | М | РГ | 0,40 | РГ | 0,40 |
Опорная поверхность станины | +pС5 | Гр | Нк | Гр | 0,40 | Нк | 0,50 |
Mах диаметр заготовки, мм | +pС6 | 100 | 630 | 200 | 0,19 | 400 | 0,57 |
Mах длина заготовки, мм | +pС7 | 180 | 3000 | 1000 | 0,30 | 800 | 0,22 |
Mах масса заготовки, кг | +pС8 | 12 | 200 | 25 | 0,05 | 80 | 0,36 |
Частота вращения шпинделя, об/мин | +pС9 | 1600 | 4000 | 2500 | 0,38 | 3150 | 0,65 |
Мощность привода шпинделя, кВт | +pС10 | 4 | 50 | 11 | 0,15 | 45 | 0,89 |
Mах подача по X, мм/мин | +pС11 | 500 | 5000 | 1000 | 0,00 | 4000 | 0,33 |
Mах подача по Z, мм/мин | +pС12 | 1000 | 10000 | 1000 | 0,00 | 4000 | 0,33 |
Погрешность позиционирования, мкм | -pС13 | 10 | 3 | 10 | 0,00 | 8 | 0,29 |
Ёмкость накопителя инструментов, шт | +pС14 | 4 | 12 | 12 | 1,00 | 12 | 1,00 |
Габарит станка по длине, мм | -pС15 | 1680 | 10000 | 3200 | 0,82 | 4500 | 0,66 |
Габарит станка по ширине, мм | -pС16 | 1040 | 3100 | 2200 | 0,44 | 2750 | 0,15 |
Габарит станка по высоте, мм | -pС17 | 1600 | 2600 | 1600 | 1,00 | 2470 | 0,10 |
Масса станка, кг | -pС18 | 1850 | 16000 | 4000 | 0,85 | 9000 | 0,49 |
Нормализованные параметрические описания станка 16А20Ф3≡mА1 и станка РТ777Ф3≡mА2 : | |||||||
Q1={0,40, 0,50, 0,50, 0,40, 0,40, 0,19, 0,30, 0,05, 0,38, 0,15, 0,00 0,00, 0,00 1,00, 0,82, 0,44, 1,00, 0,85} | |||||||
Q2={0,40, 0,50, 0,50, 0,40, 0,50, 0,57, 0,22, 0,36, 0,65, 0,89, 0,33, 0,33, 0,29, 1,00, 0,66, 0,15, 0,10, 0,49} | |||||||
*) Значения параметров pimin и pimax установлены из характеристик станков 16А20Ф3,16Б16Т 16М30Ф3, ТПК125А1-1, РТ777Ф3, САТ150, САТ630, СТМ100П40С, 1П756Ф3.
Полученные нами векторы Qk={qi=[1,I=18]}k=[1,K=2] (табл. 6) могут быть симплифицированы исключением из них критериев qi, имеющих равные парные значения (qi1=qi2). Поскольку симплификация Q1 и Q2 не изменит общую картину оптимизационного выбора, но упростит выполнение предстоящих вычислительных операций, ниже, в дальнейших процедурах оптимизационного выбора нами будут использованы векторы симплифицированного вида QS1 и QS2.
Таблица 6
Векторы критериев оптимизационного выбора
Qk | q1 | q2 | q3 | q4 | q5 | q6 | q7 | q8 | q9 | q10 | q11 | q12 | q13 | q14 | q15 | q16 | q17 | q18 |
Простые векторы оптимизационных критериев Qk | ||||||||||||||||||
Q1 | 0,40 | 0,50 | 0,50 | 0,40 | 0,40 | 0,19 | 0,3 | 0,05 | 0,38 | 0,15 | 0,00 | 0,00 | 0,00 | 1,00 | 0,82 | 0,44 | 1,00 | 0,85 |
Q2 | 0,40 | 0,50 | 0,50 | 0,40 | 0,50 | 0,57 | 0,22 | 0,36 | 0,65 | 0,89 | 0,33 | 0,33 | 0,29 | 1,00 | 0,66 | 0,15 | 0,10 | 0,49 |
Симплифицированные векторы оптимизационных критериев QSk | ||||||||||||||||||
QS1 |
|
|
|
| 0,40 | 0,19 | 0,30 | 0,05 | 0,38 | 0,15 | 0,00 | 0,00 | 0,00 |
| 0,82 | 0,44 | 1,00 | 0,85 |
QS2 |
|
|
|
| 0,50 | 0,57 | 0,22 | 0,36 | 0,65 | 0,89 | 0,33 | 0,33 | 0,29 |
| 0,66 | 0,15 | 0,10 | 0,49 |
III.2. Многокритериальное описание функции предпочтительности станка
Рассмотренные выше материалы показывают, что нормализованные описания станков Qk={qi=[1,I]}k=[1,K], являются по своей сути векторами состоятельных критериев выбора предпочтительной альтернативы OPTmАk, образованных из множества сравниваемых альтернатив МА={mАk=[1,K]}. Заметим, что в тех случаях, когда все критерии qiвносят равноценный вклад в «полезность» оцениваемой альтернативы, для определения интегрального скалярного показателя «полезности» Uk, каждой k-той альтернативы обычно применяется [9] простое аддитивное свёртывание векторов множества Qk на модели вида Uk=Σi=[1,I] qi. Однако, в подавляющем большинстве случаев мы встречаемся с доминированием одних критериев над другими. В таких случаях, для измерения вклада каждого критерия qi в интегральную оценку предпочтительности Uk, значимость критериев qiкорректируется коэффициентами весомости wi. В результате, первоначальный вектор критериев Qk={qi=[1,I]}k=[1,K] преобразуется (Рис. 4.) в вектор произведений критериев на коэффициент весомости Qk={qiх wi}k=[1,K].

Рис. 4. Общая схема «взвешивания» вектора критериев оптимизации.
Рассматриваемый нами демонстрационный пример относится ко второму случаю, предусматривающему «взвешивание» критериев оптимизации. Обычно, коэффициенты весомости оптимизационных критериев назначаются либо методом прямого экспертного оценивания, либо методом экспертного оценивания в сочетании с одним из методов парного сравнения [9]. Последнее, - более предпочтительно, так как применение парных сравнений позволяет снизить влияние фактора экспертной субъективности и, следовательно, позволяет повысить достоверность значений искомых коэффициентов весомости wi. При использовании метода парных сравнений Уэйя [10], на множестве критериев Q={qi=[1,I]} формируется матрицаD=||dii*||. Элементами dii* матрицы Dявляется экспертная оценка результата парного сравнения каждого из критериев qiтекущей i–той строки с каждым из критериев qiтекущего i*-того столбца матрицы. Причём, результат сопоставления каждой пары (qi;qi*)оценивается на трехбалльной шкале, и может принимать одно из трех значений dii*=xor[0⋁1⋁2]: dii*=2если qi⊱qi*; dii*=1если qi≡qi* и dii*=0 если qi*⊱qi. После формирования полного множества элементов матрицы D, можно расчётным путём (5) определить величины коэффициентов весомости для каждого из критериев qi., что позволяет учесть значимость каждого критерия qiумножением его на найденную величину wi.

где: D- матрица парных сравнений; dii* - оценка результата парного сравнения критерия qiтекущей i–той строки и критерия qiтекущего i*-того столбца матрицы D; wi- весовой коэффициент i–того критерия оптимизации qiоцениваемого объекта.
Найдём значения весовых коэффициентов wi для критериев оптимизации qiрассматриваемой нами демонстрационной задачи. При этом, введём два условных ограничения, которые не нарушат общей логической картины оптимизационного выбора модели станка, но позволят упростить вычислительные процедуры, выполняемые здесь «вручную»:
1. Будем рассматривать симплифицированный вариант QSkвекторов оптимизационных критериев.
2. В множестве критериев вектора QkSограничимся исследованием группы критериев {qi=[6,13]}, характеризующих технологический потенциал сравниваемых моделей.
После введения таких ограничений мощность вектора QSk будет снижена до восьми. При этом, экспертно установленное доминирование критериев {qi=[6,13]} образует убывающий вариационный ряд: (q9∧q10) ⊱ q13 ⊱ (q11∧q12) ⊱ (q1∧q2) ⊱ (q6∧q7). В этом случае, коэффициенты весомости wi и матрица парных сравнений D будут иметь вид, показанный на рисунке 5.
Обобщение полученных выше данных позволяет описать многокритериальную функцию полезности станка выражением (6), которое аддитивно свёртывает вектор QSk={qi. х wi}k=[1,K в интегральный скалярный показатель предпочтительностиUk.
![]()

Рис. 5. Определение весовых коэффициентов методом парных сравнений
III.3. Выбор оптимальной модели станка
Таким образом, при решении задач оптимизационного выбора предпочтительной модели станка, в качестве меры предпочтительности сравниваемых моделей может быть применена интегральная функция полезности. При этом, искомая оптимальная модель, очевидно, должна иметь наибольшее значение показателя предпочтительности Uk. Поэтому процедура оптимизационного выбора (7) сводится к расчёту величины показателя Uk для каждой из сравниваемых моделей mАk , а также, из идентификации модели с максимальным значением показателя Uk, которая может быть реализована на базе продукционной модели (7).
![]()
В рассматриваемой нами задаче требуется сделать выбор токарного станка из двух моделей: 16А20Ф3≡mА1 и РТ777Ф3≡mА2. Для этих моделей интегральные показатели предпочтительности U1 и U2 равны: U1=Σi=[6,13](qi1 х wi) и U2=Σi=[6,13](qi2 х wi):
U1=Σi=[6,13](qi1х wi) = (q6,1 х w6)+(q7,1 х w7)+(q8,1 х w8)+(q9,1 х w9)+(q10,1 х w10)+(q11,1 х w11)+(q12,1 х w12)+(q13,1 х w13)=(0,19 х 0,04)+(0,30 х 0,04)+(0,05 х 0,02)+(0,38 х 0,23)+(0,15 х 0,23)++(0,00 х 0,13)+ (0,00 х 0,13)+(0,00 х 0,18)=0,142
U2=Σi=[6,13](qi2 х wi)=(q6,2 х w6)+(q7,2 х w7)+(q8,2 х w8)+(q9,2 х w9)+(q10,2 х w10)+(q11,2 х w11)+(q12,2 х w12)+(q13,2 х wi13)==(0,57 х 0,04)+(0,22 х 0,04)+(0,36 х 0,02)+(0,65 х 0,23)+(0,89 х 0,23)+
+(0,33 х 0,13)+(0,33 х 0,13)+(0,29 х 0,18)=0,585
В результате вычисления значений U1 и U2 мы получаем следующий результат:
U ={U1,U2}={0,142, 0,585}
![]()
Поэтому, в соответствии с правилом (7), для обработки детали «Вал быстроходный» мы выбираем станок РТ777Ф3≡mА2.
Полученный нами результат показывает, что процедура выбора модели станка, являясь областью интеллектуальной инженерной деятельности, поддаётся формализации и, следовательно, обладает необходимыми предпосылками для автоматизации в составе САПР ТП.
Общий алгоритм рассмотренного в работе формализованного подхода к выбору оптимизационного выбора предпочтительной модели станка представлен га рисунке 6.

Рис. 6. Общий алгоритм выбор модели металлорежущего станка.
Заключение
В современной практике технологического проектирования выбор модели станка обычно осуществляется по двухэтапной схеме: этап 1 – выявление множества потенциально приемлемых моделей станка; этап 2 - выбор наиболее предпочтительной модели из числа потенциально приемлемых альтернатив. Выполнение первого этапа требует выявления в исходном семействе станков ограниченного множества станков, которые отвечают задающим ограничительным условиям проектируемой технологической операции. Выполнение второго этапа требует выбора из ограниченного множества станков наиболее предпочтительной модели по совокупности заданных оценочных критериев.
В настоящее время существуют необходимые теоретические предпосылки для формализации, как первого, так и второго этапов выбора. Работы первого этапа могут быть формализованы с применением инструментов сравнительного анализа цифровых и вербальных переменных. Работы второго этапа могут быть формализованы с применением методов многокритериального оптимизационного выбора. Обе названые методологи обладают возможностями для их использования, как в автоматизированном, так и в «ручном» вариантах.
Апробация названных методологий на примере решения практической задачи выбора, подтверждает возможность применения обсуждаемых в работе инструментов для формализации процедуры выбора предпочтительной модели станка при проектировании технологических процессов механической обработки.
Список литературы
1. Норенков И.П. Основы автоматизированного проектирования. 3-е изд., перераб. и доп. М.: .: Изд-во МГТУ им. Н.Э. Баумана, 2006. 446 с. (Информатика в техническом университете).
2. Евгенев Г.Б. Интеллектуальные системы проектирования. М.: Изд-во МГТУ им. Н.Э. Баумана, 2009. 334 с.
3. Лазаренко Г.П. Сравнительный анализ металлорежущих станков при технологическом проектировании // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2013. № 3. Режим доступа: http://technomag.bmstu.ru/doc/541242.html (дата обращения 01.11.2013).
4. Технология машиностроения: В 2 т. Т. 1. Основы технологии машиностроения: учебник для вузов / В.М. Бурцев, А.С. Васильев, А.М. Дальский и др.; Под ред. А.М. Дальского. М.: Изд-во МГТУ им. Н.Э. Баумана. 1999. 564 с.
5. Мельников Г.Н., Вороненко П.И. Проектирование механосборочных цехов: учебник для студентов машиностроительных специальностей вузов / Под ред. А.М. Дальского. М.: Машиностроение, 1990. 352 с.
6. Орлов А.И. Прикладная статистика. М.: Изд-во «Экзамен», 2007. 672 с.
7. Harrington E.C. The Desirability Function // Industrial Quality Control. 1965. Vol. 21, no. 10. P. 494-498.
8. Анохин А.М., Глотов В.А., Павельев В.В., Черкашин А.М. Методы определения коэффициентов важности критериев // Автоматика и телемеханика. 1997. № 8. С. 3-35.
9. Бобровников Г.Н., Клебанов А.И. Прогнозирование в управлении техническим уровнем и качеством продукции. М.: Изд-во стандартов, 1984.
10. Wei T.H. The algebraic foundations of ranking theory. Ph.D. Theses. Cambridge University, London, 1952.
Публикации с ключевыми словами: металлорежущие станки, принятие решений, технологическое проектирование, выбор модели, многопараметрическая оптимизация
Публикации со словами: металлорежущие станки, принятие решений, технологическое проектирование, выбор модели, многопараметрическая оптимизация
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



