научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 09, сентябрь 2013
DOI: 10.7463/0913.0623058
УДК 537.876
Россия, Москва, ФГУП «ЦНИРТИ им. академика А.И. Берга»,
Россия, МГТУ им. Н.Э. Баумана
1. Введение
В настоящее время человеческие знания о процессах дифракции электромагнитных волн (ЭМВ) сверхвысоких частот (СВЧ) достигли высокого уровня, позволяющего перенести трудоемкие и дорогостоящие эксперименты по оценке эффективной поверхности рассеяния (ЭПР) объектов из безэховых камер и полигонов в компьютерные высокопроизводительные процессоры. Рынок предлагает современные программные продукты для расчета ЭПР объектов, преимущественно зарубежные: CSTMicrowaveStudio, EMPro(разработки AgilentTechnologies), HFSS. Существуют и отечественные аналоги: FEKO, «Анализ радиолокационных характеристик объектов сложной формы» (разработки МГТУ им. Н.Э. Баумана). Разработчики указанных программных продуктов доводят их до потребителя, как правило, без предоставления каких-либо конкретных сведений о точности вычислений, а также о степени соответствия значений ЭПР объектов, рассчитанных в программе и определенных на практике. Поскольку все больше и больше коллег берут на вооружение указанные программные продукты, вопросы точности и соответствия практическим результатам их вычислений приобретают интерес и актуальность. Данные вопросы исследовались коллегами, в основном, применительно к коэффициентам стоячей волны (КСВ) и диаграммам направленности (ДН) антенн в русле популярной в настоящее время тенденции к миниатюризации антенн. Так, в [1–2] приведены результаты сравнения расчетных (с помощью указанных программных продуктов, а также ADS Momentum, MAGMAS 3D, IE3D) и экспериментальных данных для КСВ и ДН некоторых печатных антенн. Встречаются и другие параметры для сравнения. Так, в [3] авторы сравнивают расчетные (µWave Wizard, CSTMicrowaveStudio, HFSS) и экспериментальные данные для S-параметров волноводного двухмодового фильтра. В [4] авторы сравнивают электромагнитные поля (смоделированное в HFSSи CSTMicrowaveStudioи определенное экспериментально) многовитковой катушки индуктивности. В работе [5], наиболее близкой к теме настоящей статьи, авторы приводят расчетные (CSTMicrowaveStudio) и экспериментальные данные для ЭПР аппарата NASA на СВЧ. При этом методика сравнения [1–5] ограничилась визуальным сопоставлением графиков искомых функций и отношением значений какого-либо одного параметра (например, резонансной частоты). В то же время о системном изучении вопросов точности указанных программных продуктов и соответствия практическим результатам их вычислений при расчете ЭПР объектов не известно. В настоящей статье авторы докладывают о результатах работы, явившейся начальным этапом изучения точности компьютерных программ по расчету ЭПР объектов и соответствия результатов вычислений этих программ практическим результатам. Данное изучение призвано ответить на вопрос, в какой степени можно доверять современным компьютерным программам в части расчета ЭПР объектов. Данное изучение, безусловно, актуально, и его результаты вызывают большой интерес у коллег. В работе, проведенной авторами, значения ЭПР некоторых предметов, рассчитанные в CSTMicrowaveStudio (версия 2012) и «Анализ радиолокационных характеристик объектов сложной формы», сравнивались с измеренными значениями ЭПР этих предметов, и делался вывод о точности использованных компьютерных программ. Причем авторы попытались формализовать процедуру сравнения диаграмм ЭПР предметов с помощью характеристических коэффициентов, среднеквадратичных ошибок и критериев для них, определенных ниже, чтобы облечь степень соответствия данных в объективный, численный вид (чего не было в работе [5]). В результате было выявлено хорошее соответствие расчетных и экспериментальных данных.
2. Постановка задачи работы
В работе с помощью современных компьютерных программ для расчета ЭПР объектов на СВЧ CSTMicrowaveStudio 2012 и «Анализ радиолокационных характеристик объектов сложной формы» рассчитывались угловые диаграммы ЭПР некоторых предметов сравнительно простой геометрической формы. Под угловой диаграммой ЭПР объекта понималась зависимость ЭПР объекта от угла падения ЭМВ СВЧ на объект в случае моностатической локации на определенной частоте ЭМВ. Каждый объект работы обладал осевой симметрией, так что расчет ЭПР каждого объекта производился в диапазоне углов облучения 0°±90° при вращении объекта вокруг оси симметрии. Затем диаграммы ЭПР объектов работы определялись экспериментально. Диаграммы ЭПР объектов работы, рассчитанные в CSTMicrowaveStudio 2012 и «Анализ радиолокационных характеристик объектов сложной формы» (далее – расчетные диаграммы), сравнивались со своими аналогами, определенными экспериментально (далее – экспериментальными диаграммами). Для выявления степени соответствия расчетных и экспериментальных диаграмм объектов работы использовались авторские параметры (не претендовавшие на строгость и однозначность): характеристический коэффициент rи среднеквадратичная ошибка σ. r и σ были определены следующим образом:
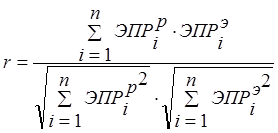 ,
, 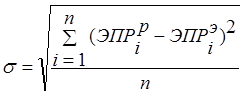 , (1)
, (1)
где n – количество углов падения ЭМВ СВЧ на объект, ЭПРiР – расчетное значение ЭПР объекта при i-ом угле падения ЭМВ СВЧ на объект, ЭПРiЭ – экспериментальное значение ЭПР объекта при i-ом угле падения ЭМВ СВЧ на объект. Характеристический коэффициент r характеризует степень линейной зависимости между расчетными и экспериментальными значениями ЭПР объекта, определенными при n углах падения ЭМВ СВЧ на объект. Смысл характеристического коэффициента r можно пояснить, если представить каждую из сравниваемых диаграмм в виде вектора в n-мерном пространстве (i-ая компонента n-мерного вектора соответствует значению ЭПР объекта при i-ом угле падения ЭМВ СВЧ на объект). Тогда значение r, определяемое (1), равно косинусу угла между векторами диаграмм в n-мерном пространстве, а выражение (1) для расчета r, по сути, есть скалярное произведение нормированных n-мерных векторов диаграмм. Значение r лежит в пределах от -1 (линейная зависимость между расчетными и экспериментальными значениями ЭПР объекта с отрицательным коэффициентом пропорциональности) до 1 (линейная зависимость между расчетными и экспериментальными значениями ЭПР объекта с положительным коэффициентом пропорциональности) включительно. Чем ближе значение r к единице, тем лучше соответствие расчетных и экспериментальных диаграмм объекта. Среднеквадратичная ошибка σ характеризует абсолютное среднее (по диапазону углов падения ЭМВ СВЧ на объект) значение разности между расчетным и экспериментальным значениями ЭПР объекта. r и σ позволяли в первом приближении просто и наглядно оценить степень соответствия расчетных и экспериментальных диаграмм объектов работы. Критериями хорошего соответствия расчетной и экспериментальной диаграмм служили r≥0,965 (угол между n-мерными векторами расчетной и экспериментальной диаграмм объекта работы – arcos(r) – не превышает 15°) и σ ≤ 1 м2. Данные значения критериев также являются авторскими и не претендуют на строгость и однозначность. r и σ в первом приближении характеризовали точность CSTMicrowaveStudio 2012 и «Анализ радиолокационных характеристик объектов сложной формы» при вычислении расчетных диаграмм. Таким образом, суть представляемой работы – определение характеристических коэффициентов r и среднеквадратичных ошибок σ между расчетными и экспериментальными диаграммами объектов работы; по значениям характеристических коэффициентов и среднеквадратичных ошибок делался вывод о точности CSTMicrowaveStudio 2012 и «Анализ радиолокационных характеристик объектов сложной формы» и соответствии их результатов практическим результатам. Работа проводилась на частотах ЭМВ 3 ГГц, 6 ГГц, 10 ГГц.
Объекты работы (пять объектов) по конструктивному признаку можно было разделить на две группы: 1) конструктивно выполненные исключительно из металла, 2) конструктивно выполненные из металла и диэлектрика. Такое разделение объектов работы было введено, чтобы отдельно оценить точность использованных компьютерных программ при работе с металлическими объектами (задаваемыми в компьютерных программах как PEC– PerfectElectricConductor) и объектами, выполненными, помимо металла, также из диэлектрика с известной диэлектрической проницаемостью ε. В первую группу входили два объекта работы: плоский квадратный алюминиевый лист размером 400 мм×400 мм×4 мм (объект № 1), весло (объект № 2) – объект несложной геометрической формы, изображенный на рисунке 1. Во вторую группу входили три объекта работы: плоский квадратный алюминиевый лист, на одну из сторон которого был нанесен (с помощью двустороннего скотча) плоский квадратный лист из диэлектрического материала СП10 с диэлектрической проницаемостью ε 7,8 (рисунок 2, объект № 3); плоский квадратный алюминиевый лист, на всю одну из сторон которого было нанесено покрытие из диэлектрика с ε 4 (рисунок 3, объект № 4); весло, изображенное на рисунке 1, на всю лопасть которого было нанесено покрытие (толщиной 2 мм) из диэлектрика с ε 4 (объект № 5). Значения диэлектрической проницаемости ε диэлектриков были измерены в [6].
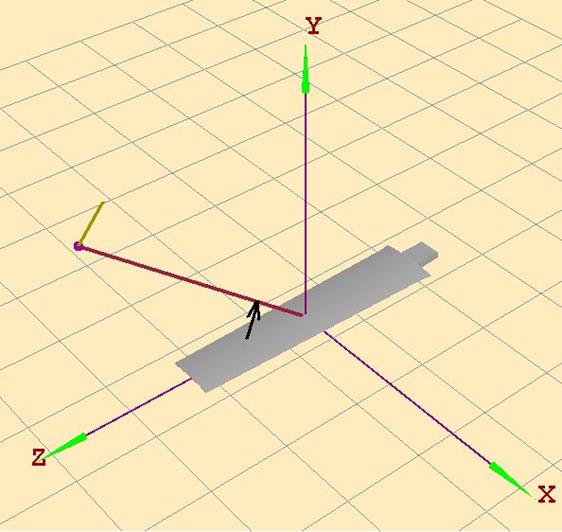
Рисунок 1 – внешний вид объекта работы весло в графическом редакторе компьютерной программы «Анализ радиолокационных характеристик объектов сложной формы»
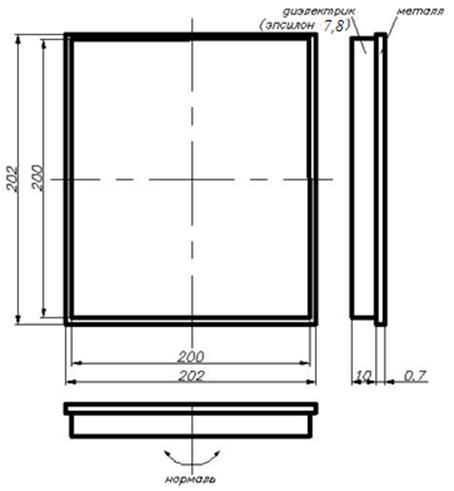
Рисунок 2 – объект работы № 3
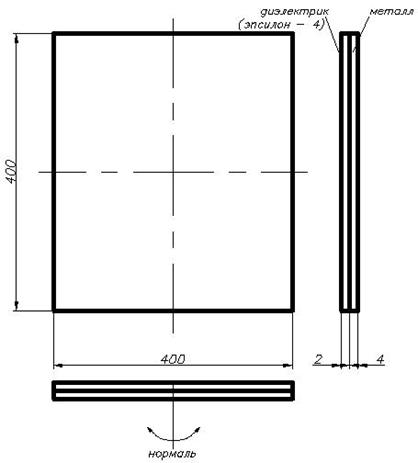
Рисунок 3 – объект работы № 4
3. Теоретическая часть
Алгоритм вычисления ЭПР объекта программой «Анализ радиолокационных характеристик объектов сложной формы» рассмотрен в [7–9]. Кратко приведем основные его положения. Программа предназначенадля вычисления ЭПР объектов, размеры которых много больше (на порядок и более) длины волны зондирующего электромагнитного излучения (ЭМИз). Для вычисления ЭПР объекта программа строит полигональную модель объекта (с помощью средств CreoElementsPro), состоящую из отдельных плоских элементов-треугольников (с размерами, много меньшими длины волны зондирующего ЭМИз) – фацетов; т.е., объект представляется в виде совокупности фацетов. Далее программа проводит анализ незатененных и немаскируемых фацетов, а также незатененных и немаскируемых острых кромок, которые могут быть образованы некоторыми фацетами. Программа вычисляет суммарное электрическое поле ЕΣ в апертуре приемной антенны, складывающееся из полей, рассеянных каждым незатененным элементарным отражателем (ЭО) – фацетом или острой кромкой – при падении на него зондирующего ЭМИз, а также вторичного поля Е2, рассеянного немаскируемыми ЭО при падении на них ЭМИз, переотраженного фацетами:
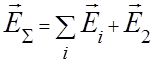 , (2)
, (2)
где![]() – напряженность электрической составляющей электромагнитного поля (ЭМП), рассеянного в апертуру приемной антенны i-м ЭО при падении на него зондирующего ЭМИз. Рассеянное в апертуру приемной антенны плоским треугольным фацетом (при падении на него как зондирующего ЭМИз, так и ЭМИз, переотраженного фацетами) ЭМП вычисляется с помощью законов физической оптики, конкретно – интеграла Стреттона — Чжу:
– напряженность электрической составляющей электромагнитного поля (ЭМП), рассеянного в апертуру приемной антенны i-м ЭО при падении на него зондирующего ЭМИз. Рассеянное в апертуру приемной антенны плоским треугольным фацетом (при падении на него как зондирующего ЭМИз, так и ЭМИз, переотраженного фацетами) ЭМП вычисляется с помощью законов физической оптики, конкретно – интеграла Стреттона — Чжу:
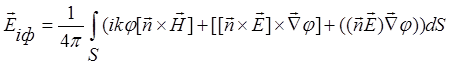 , (3)
, (3)
где![]() – напряженность электрической составляющей указанного ЭМП, S– площадь фацета, 𝜑 – векторная функция Грина,
– напряженность электрической составляющей указанного ЭМП, S– площадь фацета, 𝜑 – векторная функция Грина, ![]() – электрическое поле на поверхности фацета,
– электрическое поле на поверхности фацета, ![]() – магнитное поле на поверхности фацета,
– магнитное поле на поверхности фацета, ![]() –нормаль к плоскости фацета, k– волновой вектор ЭМИз в свободном пространстве. Рассеянное в апертуру приемной антенны идеально проводящей острой кромкой (при падении на нее как зондирующего ЭМИз, так и ЭМИз, переотраженного фацетами) ЭМП вычисляется с помощью законов физической теории дифракции [10]:
–нормаль к плоскости фацета, k– волновой вектор ЭМИз в свободном пространстве. Рассеянное в апертуру приемной антенны идеально проводящей острой кромкой (при падении на нее как зондирующего ЭМИз, так и ЭМИз, переотраженного фацетами) ЭМП вычисляется с помощью законов физической теории дифракции [10]:
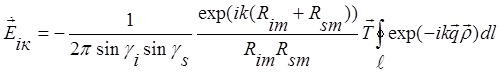 , (4)
, (4)
где ![]() – напряженность электрической составляющей указанного ЭМП,
– напряженность электрической составляющей указанного ЭМП, ![]() – базис в локальной системе координат кромки,
– базис в локальной системе координат кромки, ![]() – разность между вектором Умова — Пойтинга падающего ЭМИз и вектором Умова — Пойтинга рассеянного кромкой ЭМИз, l – длина кромки, γi– разность между вектором Умова — Пойтинга падающего ЭМИз и базисом локальной системы координат кромки, γs– разность между вектором Умова — Пойтинга рассеянного кромкой ЭМИз и базисом локальной системы координат кромки, Rim – расстояние между фазовым центром излучающей антенны и началом локальной системы координат кромки, Rsm – расстояние между фазовым центром приемной антенны и началом локальной системы координат кромки,
– разность между вектором Умова — Пойтинга падающего ЭМИз и вектором Умова — Пойтинга рассеянного кромкой ЭМИз, l – длина кромки, γi– разность между вектором Умова — Пойтинга падающего ЭМИз и базисом локальной системы координат кромки, γs– разность между вектором Умова — Пойтинга рассеянного кромкой ЭМИз и базисом локальной системы координат кромки, Rim – расстояние между фазовым центром излучающей антенны и началом локальной системы координат кромки, Rsm – расстояние между фазовым центром приемной антенны и началом локальной системы координат кромки, ![]() – пространственный коэффициент, включающий коэффициенты дифракции Уфимцева.
– пространственный коэффициент, включающий коэффициенты дифракции Уфимцева.
Переотраженное фацетами ЭМП вблизи немаскируемых ЭО вычисляется с использованием законов геометрической оптики; в зарубежной литературе такой подход носит название метода прыгающих и отскакивающих лучей – Shootingandbouncingrays (SBR). По формулам Френеля определяется переотраженное плоским треугольным фацетом ЭМП вблизи немаскируемых ЭО. Затем по формулам (3), (4) вычисляется вторично дифрагированное (на немаскируемых ЭО) ЭМП в апертуре приемной антенны.
ЭПР σ объекта вычисляется через известное радиолокационное соотношение [11]:
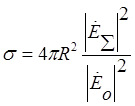 , (5)
, (5)
где R – расстояние между объектом и приемной антенной, ![]() – напряженность электрического поля зондирующего ЭМИз вблизи объекта.
– напряженность электрического поля зондирующего ЭМИз вблизи объекта.
Для вычисления ЭПР объектов работы использовался модуль A-Solverв CSTMicrowaveStudio 2012, применяющийся при размерах объекта, много больших (на порядок и более) длины волны зондирующего ЭМИз. Данный модуль позиционируется фирмой-разработчиком как компромисс между точностью и скоростью вычислений (сравнительно высокая точность при относительно малом времени вычислений). Алгоритм вычисления ЭПР объекта программой CSTMicrowaveStudio 2012 фирма-разработчик не раскрывает, однако, по данным [12] он сходен с алгоритмом российского «Анализа радиолокационных характеристик объектов сложной формы». В представляемом исследовании вычисления в CSTMicrowaveStudio 2012 A-Solverпроизводились при настройках, ориентировавших расчет на высокую точность: параметры SolverSettings: Solver– SBRRaytubes, Accuracy– High, Maximumnumberofreflections – 3.
4. Практическая часть
Экспериментальные диаграммы объектов работы измерялись по классической схеме измерения ЭПР объекта в безэховой камере (БЭК), подразумевающей измерение мощности сигнала, отраженного объектом, на определенной частоте ЭМИз (т.е., измерения проводились в частотной области). Перед измерениями экспериментальных диаграмм объектов работы был измерен паразитный фон БЭК, который был запомнен и вычитался из сигналов объектов работы. Использовалась антенна П6-59, которая была неподвижна и работала как на прием, так и на передачу, и векторный анализатор цепей (ВАЦ) Agilent E8362B. Объект работы устанавливался напротив приемопередающей антенны в поворотное устройство, которое медленно поворачивало объект работы на 180° относительно исходного положения. Таким образом, ВАЦ снимал экспериментальную диаграмму объекта работы.
Объекты № 1, 3, 4 работы устанавливались напротив антенны так, что плоскость листа была перпендикулярна прямой, проходящей через центр листа и фазовый центр антенны (установка осуществлялась с помощью красного лазера). Данное положение объекта № 1, 3, 4 работы соответствовало углу 90° на экспериментальной диаграмме. Углы 0° и 180° на экспериментальной диаграмме в случае объектов № 1, 3, 4 работы соответствовали случаю, когда лист находился ребром к антенне. Т.е., в случае объектов № 1, 3, 4 работы поворотное устройство поворачивало лист вокруг его вертикальной оси симметрии, как показано стрелками, например, на рисунке 2. Объекты № 2, 5 работы поворачивались в поворотном устройстве вокруг оси Х (рисунок 1) при том, что вектор Умова — Пойтинга зондирующего ЭМИз лежал на оси Y. При этом положение, при котором весло находилось лопастью анфас к антенне, соответствовало углу 90° на экспериментальной диаграмме.
5. Результаты и обсуждение
При определении точности вычислений использованных компьютерных программ концептуально экспериментальные диаграммы объектов работы принимались в качестве эталонов, отклонения от которых и определяли точность использованных программ. Расчетные и экспериментальные диаграммы объектов работы приведены на рисунках 4–10. Искомые характеристические коэффициенты и среднеквадратичные ошибки приведены в таблицах 1–2.
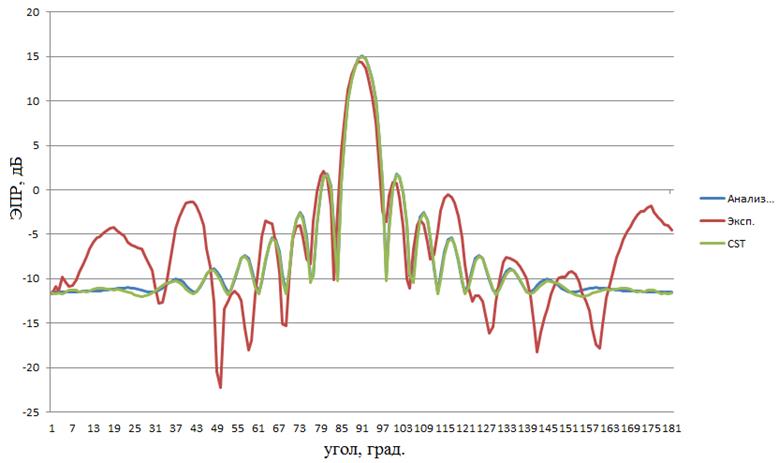
Рисунок 4 – расчетные и экспериментальная диаграммы объекта №1 работы, 3ГГц, горизонтальная поляризация зондирующего ЭМИз
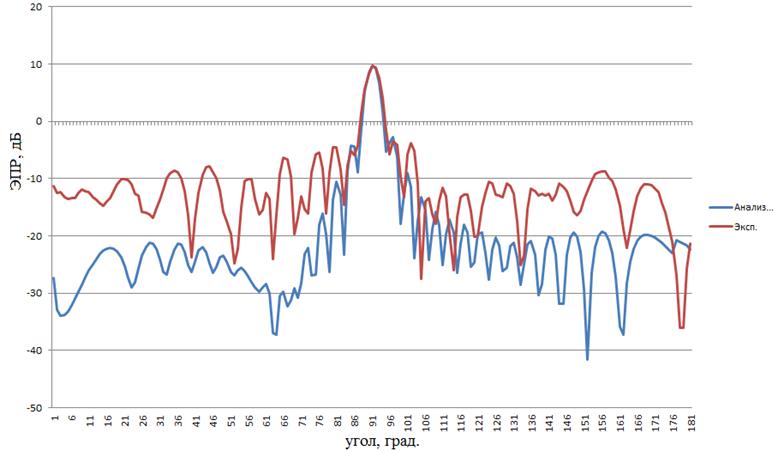
Рисунок 5 – расчетная и экспериментальная диаграммы объекта №2 работы, 3ГГц, вертикальная поляризация зондирующего ЭМИз
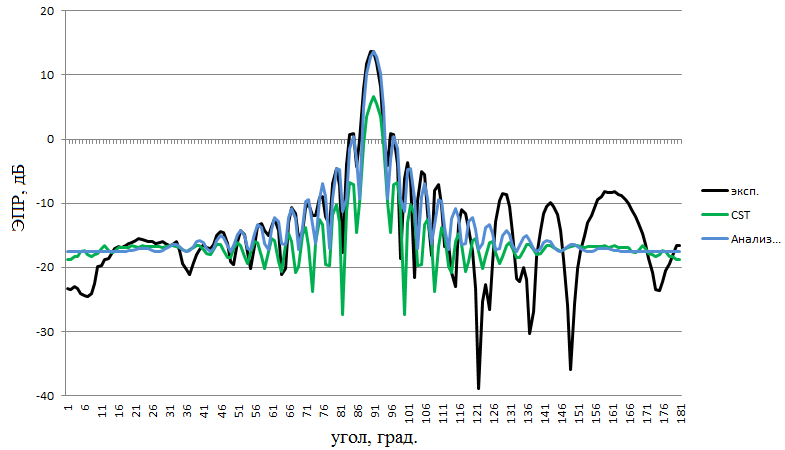
Рисунок 6 – расчетные и экспериментальная диаграммы объекта №3 работы, 10ГГц, горизонтальная поляризация зондирующего ЭМИз
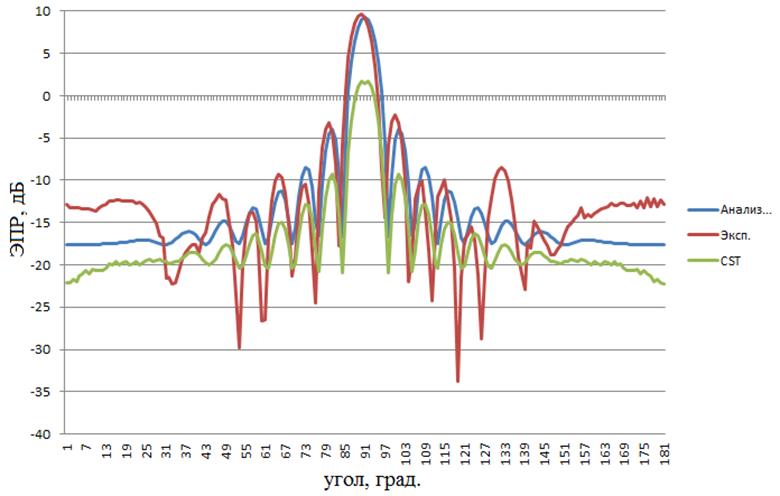
Рисунок 7 – расчетные и экспериментальная диаграммы объекта №3 работы, 6ГГц, горизонтальная поляризация зондирующего ЭМИз
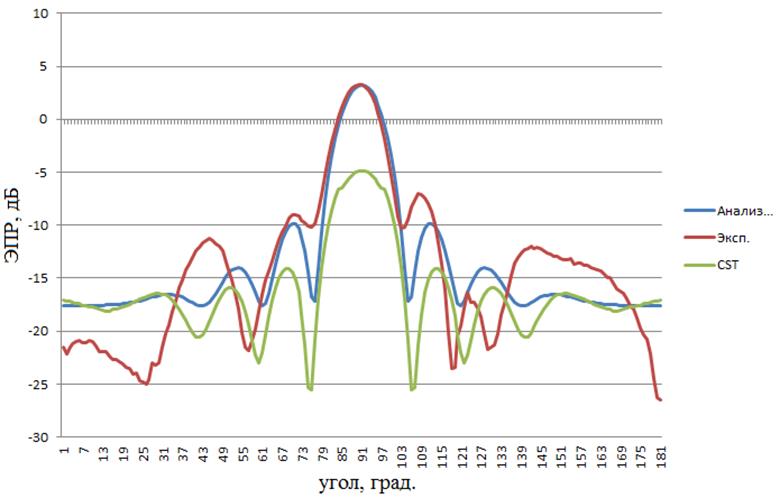
Рисунок 8 – расчетные и экспериментальная диаграммы объекта №3 работы, 3ГГц, вертикальная поляризация зондирующего ЭМИз
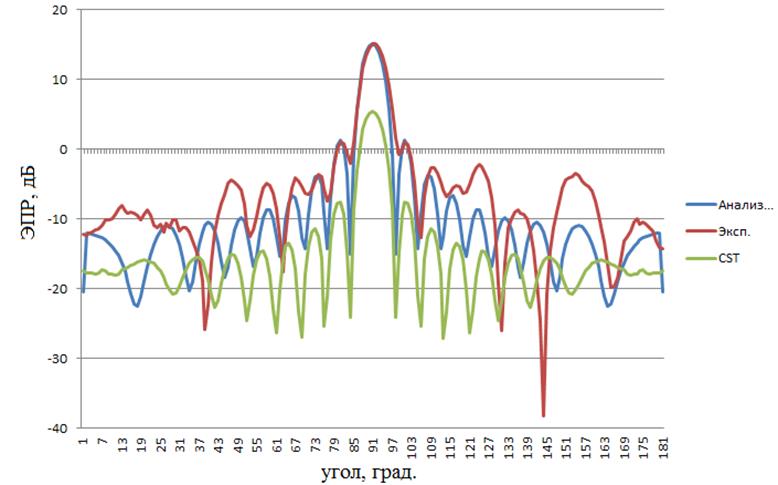
Рисунок 9 – расчетные и экспериментальная диаграммы объекта №4 работы, 3ГГц, вертикальная поляризация зондирующего ЭМИз
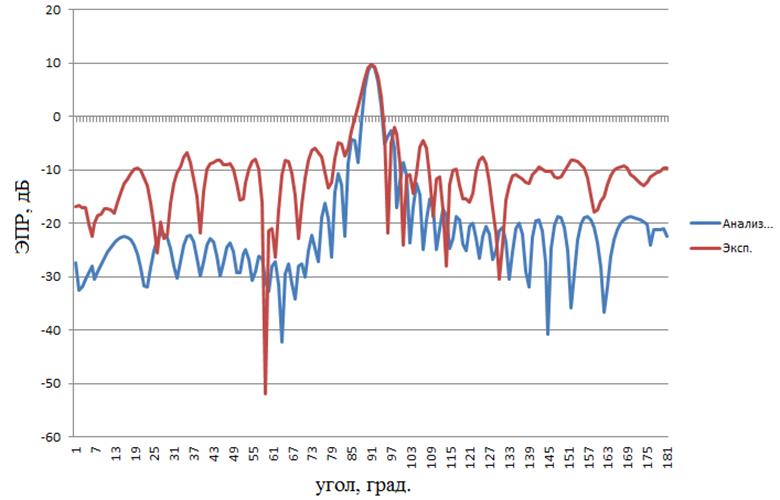
Рисунок 10 – расчетная и экспериментальная диаграммы объекта №5 работы, 3ГГц, вертикальная поляризация зондирующего ЭМИз
Таблица 1. Характеристические коэффициенты и среднеквадратичные ошибки между расчетными («Анализ радиолокационных характеристик объектов сложной формы») и экспериментальными диаграммами объектов работы
Объект работы | Характеристический коэффициент/среднеквадратичная ошибка, м2 | ||
f=10 ГГц | f=6ГГц | f=3 ГГц | |
Объект №1 | – | – | 0,981121/1,1142 |
Объект №2 | – | – | 0,992087/0,165 |
Объект №3 | 0,974794/0,6613 | 0,94443/0,46519 | 0,98995/0,06424 |
Объект №4 | – | – | 0,98786/4,6292 |
Объект №5 | – | – | 0,981837/0,2755 |
Таблица 2. Характеристические коэффициенты и среднеквадратичные ошибки между расчетными (CSTMicrowaveStudio 2012 A-Solver) и экспериментальными диаграммами объектов работы
Объект работы | Характеристический коэффициент/среднеквадратичная ошибка, м2 | ||
f=10 ГГц | f=6 ГГц | f=3 ГГц | |
Объект №1 | – | – | 0,98118/1,07177 |
Объект №2 | – | – | – |
Объект №3 | 0,97404/2,4641 | 0,94284/1,2188 | 0,96817/0,40136 |
Объект №4 | – | – | 0,9892/4,7858 |
Объект №5 | – | – | – |
Для полноты работы использовалась как горизонтальная, так и вертикальная поляризация зондирующего ЭМИз. Как видно на рисунках 4–10 и из таблиц 1–2, расчетные и экспериментальные диаграммы довольно схожи. Так, в шести из семи случаев использования «Анализа радиолокационных характеристик объектов сложной формы» искомый характеристический коэффициент превысил значение критерия, и только однажды оказался меньше: для объекта № 3 на 6 ГГц (таблица 1). Не менее успешен оказался и CSTMicrowaveStudio 2012 A-Solver: из пяти случаев в четырех искомый характеристический коэффициент превысил значение критерия, и только однажды оказался меньше: для объекта № 3 на 6 ГГц (таблица 2). При использовании «Анализа радиолокационных характеристик объектов сложной формы» искомые среднеквадратичные ошибки также оказались достаточно малы: в пяти из семи случаев они оказались меньше значения критерия, и только в двух (объект № 1 на 3 ГГц, объект № 4 на 3 ГГц) превысили его. Хуже дела обстояли при использовании CSTMicrowaveStudio 2012 A-Solver: в четырех из пяти случаев искомая среднеквадратичная ошибка превысила значение критерия, и лишь в одном (объект № на 3 ГГц) оказалось меньше его. Однако, параметр точности вычислений в виде среднеквадратичной ошибки был не совсем объективен в случае использования CSTMicrowaveStudio 2012 A-Solver, поскольку калибровка экспериментальных диаграмм выполнялась по значениям ЭПР объектов работы, вычисленным «Анализом радиолокационных характеристик объектов сложной формы» при 90°, т.е. «Анализ радиолокационных характеристик объектов сложной формы» априори находился в лучших условиях в плане малости искомых среднеквадратичных ошибок, чем его зарубежный аналог. Таким образом, основываясь на результатах таблицы 1, в первом приближении можно положить, что точность вычислений ЭПР объектов «Анализом радиолокационных характеристик объектов сложной формы», характеризуемая найденными среднеквадратичными ошибками, составляет не хуже ± 5 м2, что является положительным результатом для программы оценки ЭПР объектов, в особенности крупных, с ЭПР более 100 м2. Если принимать во внимание исключительно найденные характеристические коэффициенты (таблицы 1, 2), то обе использованные программы показали приблизительно равную высокую точность вычислений ЭПР объектов работы.
Следует отметить, что в центральной части (в области главного лепестка – 75°…105°) расчетные и экспериментальные диаграммы достаточно близки (что видно визуально на рисунках 4–10). В области же боковых лепестков наблюдаются значительные расхождения. Они, по-видимому, объясняются недостаточно высокой точностью измерения ЭПР объектов работы в области боковых лепестков ввиду того, что прималом уровне ЭПР объекта работы -10 дБ (0,1 м2), характерном для области боковых лепестков, влияние шумов измерительной аппаратуры и нескомпенсированного паразитного сигнала от БЭК затрудняет корректную оценку сигнала от объекта.
Характеристические коэффициенты и среднеквадратичные ошибки между расчетными диаграммами объектов работы, полученными с помощью CSTMicrowaveStudio 2012 A-Solver и «Анализ радиолокационных характеристик объектов сложной формы», приведены в таблице 3.
Таблица 3. Характеристические коэффициенты и среднеквадратичные ошибки между расчетными («Анализ радиолокационных характеристик объектов сложной формы» и CSTMicrowaveStudio 2012 A-Solver) диаграммами объектов работы
Объект работы | Характеристический коэффициент/среднеквадратичная ошибка, м2 | ||
f=10 ГГц | f=6ГГц | f=3 ГГц | |
Объект №1 | – | – | 1/0,06965 |
Объект №2 | – | – | – |
Объект №3 | 0,99811/2,3424 | 0,99774/1,099 | 0,98225/0,3977 |
Объект №4 | – | – | 0,9992/4,6292 |
Объект №5 | – | – | – |
Высокие значения характеристических коэффициентов из таблицы 3 (все – выше значения критерия) между расчетными диаграммами объектов работы, полученными с помощью CSTMicrowaveStudio 2012 A-Solver и «Анализ радиолокационных характеристик объектов сложной формы», свидетельствуют о близком сходстве этих диаграмм и алгоритмов указанных программ. Однако, наличествующие в таблице 3 относительно высокие значения среднеквадратичных ошибок (три из которых превышают значение критерия) свидетельствуют о необходимости дальнейшего досконального изучения алгоритма CSTMicrowaveStudio 2012 A-Solver с целью выявления причин этих отклонений.
6. Заключение
Таким образом, в представленной работе показано, что компьютерные программы «Анализ радиолокационных характеристик объектов сложной формы» и CSTMicrowaveStudio 2012 A-Solver позволяют с достаточно хорошей точностью оценивать характер угловых диаграмм ЭПР объектов несложной геометрической формы для случая моностатической локации. При этом точность «Анализа радиолокационных характеристик объектов сложной формы» при вычислении ЭПР такого объекта в первом приближении можно оценить как ±5 м2. Конечно, представленная работа – лишь начальный этап изучения вопроса точности современных компьютерных программ для вычисления ЭПР объектов, которое, безусловно, актуально и востребовано. Необходимо дальнейшее углубленное изучение этого вопроса. В будущем авторы планируют, используя представленную методику сравнительного анализа, провести более детальную оценку точности CSTMicrowaveStudio 2012 А-Solver, расширив номенклатуру объектов работы объектами более сложной геометрической формы и усовершенствовав методику моностатического измерения ЭПР объектов в области малых значений ЭПР. Призываем коллег поддержать наше исследование, чтобы определить четкие границы использования современных компьютерных программ для вычислений ЭПР объектов.
Работа выполнена при финансовой поддержке в рамках государственного контракта № 14.513.11.0025 ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы».
Благодарности
Авторы выражают благодарность специалистам ФГУП «ЦНИРТИ им. академика А.И. Берга» Кирееву Евгению Константиновичу и Кузнецову Вячеславу Ивановичу за проведение экспериментов по оценке ЭПР, а также начальнику сектора ФГУП «ЦНИРТИ им. академика А.И. Берга» Мурлаге Алексею Ростиславовичу за помощь в организации этих экспериментов. Авторы также выражают благодарность сотрудникам кафедры СМ5 МГТУ им. Н.Э. Баумана Борзову Андрею Борисовичу и Сучкову Виктору Борисовичу за проведение вычислений в программе «Анализ радиолокационных характеристик объектов сложной формы».
Список литературы
1. Васильченко А., Схольц И., Ванденбош Г. Качественная оценка вычислительных методов электродинамики на примере программных продуктов высокочастотного моделирования микрополосковых антенн // Технологии в электронной промышленности. 2008. № 3 С. 52-56. Режим доступа: http://www.tech-e.ru/2008_3_52.php (дата обращения 01.08.2013).
2. Папилов К.Б. Численный анализ микрополосковых печатных антенн // Журнал радиоэлектроники. 2011. № 4. Режим доступа: http://jre.cplire.ru/koi/apr11/5/text.html (дата обращения 01.08.2013).
3. Колегов А.Н., Узолин Е.Ю. Тестирование систем трехмерного электромагнитного моделирования на примере волноводного двухмодового фильтра // Доклады Томского государственного университета систем управления и радиоэлектроники. 2010. № 2 (22), ч. 2. С. 45-48. Режим доступа: http://www.tusur.ru/filearchive/reports-magazine/2010-2-2/45.pdf (дата обращения 01.08.2013).
4. Kozlov M., Turner R. A Comparison of Ansoft HFSS and CST Microwave Studio Simulation Software for Multi-channel Coil Design and SAR Estimation at 7T MRI // PIERS Online. 2010. Vol. 6, no. 4. Р. 395-399. Available at: http://www.piers.org/piersonline/piers.php?volume=6&number=4&page=395 , accessed 01.08.2013.
5. An Integral Equation Solver for Military Applications // Microwave Journal. Supplement “Military Microwaves”. August 2007. Available at: http://www.microwavejournal.com/articles/5221-an-integral-equation-solver-for-military-applications , accessed 01.08.2013.
6. Разработка способов и средств снижения радиолокационной заметности самолётного реактивного двигателя в задней полусфере: отчет о НИР (заключит.) / ЦНИРТИ им. академика А.И. Берга; Руководитель А.М. Бородин. Шифр темы «Сопло–ПИ–ЦНИРТИ–3»; Инв. № 40470. М., 2012.148 с. Отв. исполн. И.А. Дамарацкий, А.Р. Мурлага и др.
7. Борзов А.Б., Соколов А.В., Сучков В.Б. Цифровое моделирование входных сигналов систем ближней радиолокации от сложных радиолокационных сцен // Успехи современной радиоэлектроники. 2004. № 9-10. С. 38-61.
8. Антифеев В.Н., Борзов А.Б., Сучков В.Б. Физические модели радиолокационных полей рассеяния объектов сложной формы: учеб. пособие. М.: Изд-во МГТУ им. Н.Э. Баумана, 2003. 63 с.
9. Методы синтеза геометрических моделей сложных радиолокационных объектов / А.Б. Борзов, Э.А. Засовин, А.В. Соколов, В.Б. Сучков // Электромагнитные волны & электронные системы. 2003. Т. 8, № 5. С. 55-63.
10. Уфимцев П.Я. Основы физической теории дифракции. М.: Бином, 2009.352 с.
11. Финкельштейн М.И. Основы радиолокации. М.: Советскоерадио, 1983. 536 с.
12. CST Microwave Studio 2012.
Публикации с ключевыми словами: точность, компьютерная программа, эффективная поверхность рассеяния, характеристический коэффициент, среднеквадратичная ошибка, безэховая камера
Публикации со словами: точность, компьютерная программа, эффективная поверхность рассеяния, характеристический коэффициент, среднеквадратичная ошибка, безэховая камера
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



