научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 09, сентябрь 2013
DOI: 10.7463/0913.0602179
Россия, МГТУ им. Н.Э. Баумана
Введение и постановка задачи
Шаговые двигатели (ШД) синхронного типа уже достаточно давно широко используются в различных устройствах точного воспроизведения заданных параметров движения [1,2]. В современных электроприводах фазные обмотки ШД обычно получают питание от инверторов, работающих в режиме управляемого источника тока [3]. В идеализированном случае питание фазных обмоток ШД от источника тока позволяет при составлении математического описания электропривода исключить из рассмотрения уравнения электрического равновесия фаз и свести его только к одному или нескольким уравнениям механического движения системы в зависимости от того, существенна ли механическая связь между его координатами [4, 5]. Из решения этих уравнений с учетом дополнительных условий аналитически или с применением вычислительной техники (в случае сложного взаимовлияния координат электропривода и существенной нелинейности магнитной системы ШД) находится закон управления, соответствующий желаемой траектории движения.
Обычно наиболее ярко выраженными неидеальностями инверторов тока являются ограниченное быстродействие и наличие высокочастотной составляющей в кривой фазного тока при импульсном регулировании [6]. Однако если параметры элементов электропривода выбраны правильно с учетом этих неидеальностей, либо для заданных параметров движения предварительно оценены максимальные ошибки, вносимые инвертором, то в дальнейшем их можно не учитывать и предполагать, что ШД питается от идеального источника тока. Рассмотрим с этих позиций ход решения задачи определения алгоритма управления, когда по условию, основным режимом работы электропривода является движение с постоянной скоростью или медленные её изменения и лишь кратковременно требуются относительно быстрое протекание динамических процессов.
Для рассматриваемого варианта электропривода может оказаться достаточным простейший алгоритм управления, при котором необходимое быстродействие электропривода достигается программное увеличением на время переходного процесса момента ШД за счет соответствующего кратковременного увеличения фазного тока [7].
Так, проведенные ранее исследования показали, что в индукторных ШД кратковременное увеличение фазного тока выше номинального значения в два раза позволяет получить примерно в 1.3 раза увеличение максимального момента. Большими возможностями в увеличении момента за счет увеличения фазного тока обладают магнитоэлектрические ШД с активным ротором, у которых в пределах 2-3 кратного увеличения фазного тока наблюдается практически пропорциональное увеличение развиваемого ими электромагнитного момента [6]. Очевидно, для практической реализации такого алгоритма управления инвертор должен быть рассчитан с учетом кратковременных перегрузок по току.
Функциональная схема шагового электропривода, работающего по такому алгоритму, показана на рисунке. 1 [7]. Задатчик величины фазного тока управляет масштабным усилителем и аналоговым коммутатором. В обычных режимах работы на вход инвертора через аналоговый коммутатор подается непосредственно сигнал задатчика фазного тока. Однако кратковременно аналоговый коммутатор, управляемый по специальной программе по дополнительному входу, подает на вход инвертора сигнал увеличенной амплитуды с выхода масштабного усилителя.

Рисунок 1 - Функциональная схема шагового электропривода с повышенным быстродействием
Описание модели и результаты моделирования
Эффективность предложенного алгоритма управления в зависимости от параметров электропривода проверялась моделированием в среде МАТЛАБ-СИМУЛИНК обобщенного уравнения движения электропривода [1], представленного в виде
![]() , (1)
, (1)
где γ, θ - углы, определяющие положение результирующей МДС статора и положение ротора ШД, соответственно; δ - относительный коэффициент внешнего демпфирования; μн – относительное значение момента нагрузки электропривода в долях амплитудного значения синхронизирующего момента ШД, t – относительное время, выраженное в долях периода собственных круговых колебаний механической части ШД Т0. Зависящий от времени коэффициент k(t) отражает кратность кратковременной форсировки по моменту. Схема имитационной модели, построенной по уравнению (1), показана на рисунке 2. Переменный коэффициент k(t) реализован в модели в виде ступенчатой зависимости, которая формируется блоками Sum1, HitCrossing, S-RFlip - Flop, Memory, K, K1, Switch.
Длительность форсировки по моменту поставлена в зависимость от текущей скорости электропривода ω. При достижении скоростью ωзаданного значения ωзад форсировка по моменту снимается.
С целью всесторонней оценки предложенного алгоритма и получения количественных соотношений на модели реализован полный факторный эксперимент ПФЭ23 [8]. В качестве независимых факторов выбраны момент нагрузки μн, коэффициент демпфирования δ и кратность форсировки по моменту k. Функции цели – безразмерная скорость ![]() и время первого согласования tс (интервал времени, за который скорость ШД в первый раз достигает заданного значения wзад). Диапазоны варьирования факторов выбраны по аналогии с [8]:
и время первого согласования tс (интервал времени, за который скорость ШД в первый раз достигает заданного значения wзад). Диапазоны варьирования факторов выбраны по аналогии с [8]:
![]() (2)
(2)
Диапазон варьирования коэффициента форсировки k выбран достаточно большим – от 1 до 5 с тем, чтобы перекрыть все возможные для практики случаи и наиболее отчетливо проследить намечающиеся тенденции при изменении того или иного фактора.

Рисунок 2 – Имитационная модель шагового электропривода.
Методика проведения каждого планового опыта состояла в следующем: задав плановое сочетание изменяемых факторов, назначалось некоторое значение скорости ωзад. На контроль выводился выход блока Sum, отражающий закон изменения динамической ошибки (γ– θ) в системе и выход блока Integrator, отражающий закон изменения скорости ![]() . Если при этом осуществлялось вхождение ШД в синхронизм, о чем свидетельствовал соответствующий закон изменения динамической ошибки (γ– θ) во времени, то опыт повторялся при увеличенном значении ωзад. Таким образом, постепенно повышая ωзад в опытах, находилось предельное её значение ωпр, т.е. скорость приемистости. Контрольный опыт, в котором скорость ωзад сколь угодно мало превышает ωпр, подтверждал правильность установленной границы: в этом опыте динамическая ошибка (γ– θ) растет неограниченно.
. Если при этом осуществлялось вхождение ШД в синхронизм, о чем свидетельствовал соответствующий закон изменения динамической ошибки (γ– θ) во времени, то опыт повторялся при увеличенном значении ωзад. Таким образом, постепенно повышая ωзад в опытах, находилось предельное её значение ωпр, т.е. скорость приемистости. Контрольный опыт, в котором скорость ωзад сколь угодно мало превышает ωпр, подтверждал правильность установленной границы: в этом опыте динамическая ошибка (γ– θ) растет неограниченно.
Примеры результатов модельного эксперимента в виде осциллограмм для динамической ошибки (γ– θ) и скорости ШД ![]() показаны на рисунках 3 и 4.
показаны на рисунках 3 и 4.
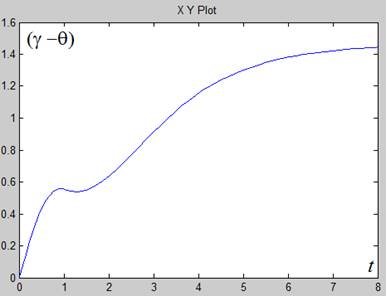

Рисунок 3 – Результаты моделирования при k=5, δ=1, μн=0.05.


Рисунок 4 – Результаты моделирования при k=5, δ=0.15, μн=0.5.
Полином для ωпр, найденный по результатам эксперимента, имеет вид:
![]() (3)
(3)
Время первого согласования может быть найдено из следующего полинома
![]() ,
,
(4)
где ![]() ;
; ![]() ;
; ![]() .
.
Из рассмотрения рисунков 3 и 4, а также других не представленных здесь результатов моделирования при иных сочетаниях изменяемых факторов в соответствии с планом модельного эксперимента можно сделать вывод о том, что предложенный простейший алгоритм управления ШД оказывается неэффективным для систем электроприводов со значительным внешним демпфированием – после снятия форсировки по моменту в скоростной характеристике ω(t) наблюдается значительный провал, достигающий 50% и более от ωзад, а затем довольно медленное «дотягивание» скорости до значения ωзад.
Выводы
1. Разработана имитационная модель шагового электропривода в среде MATLAB - SIMULINK при питании двигателя от управляемого инвертора тока, с использованием которой проверена эффективность предложенного способа управления;
2.Показано, что предлагаемый способ управления ШД наиболее эффективен для систем электропривода с малым внешним демпфированием, в частности, для приборных систем многокоординатного электропривода на аэростатической опоре, если характер технологического процесса соответствует исходной постановке задачи;
3. Установлено, что при значительном внешнем демпфировании после снятия кратковременной форсировки по моменту в скоростной характеристике ω(t) наблюдается значительный провал, достигающий 50% и более от заданного значения скорости ωзад, а затем довольно медленное «дотягивание» до ωзад;
4. Получены уравнения проектирования привода в удобной для использования полиномиальной форме, позволяющие при известных его параметрах и параметрах управления оценивать динамические показатели привода, либо при заданном быстродействии привода обоснованно выбирать его параметры.
Список литературы
1. Ивоботенко И.А., Рубцов В.П., Садовский Л.А., Цаценкин В.К., Чиликин М.Г. Дискретный электропривод с шаговыми двигателями / Под общ. ред. М.Г. Чиликина. М.: Энергия, 1971. 624 с.
2. Paul Acarnley. Stepping motors. A guide to theory and practice. 4th еd. London: Institution of Engineering and Technology, 2007. 159 p.
3. Козаченко В.Ф., Пискунов А.Г., Красовский А.Б., Грудинин В.С. Принципы построения инверторов для шагового электропривода с электрическим дроблением шага // Электротехническая промышленность. Сер. Электропривод. 1984. № 10.С. 1-4.
4. Ивоботенко Б.А., Козаченко В.Ф. Шаговый электропривод в робототехнике. М.: МЭИ, 1984. 101 с.
5. Ивоботенко Б.А., Ильинский Н.Ф., Кожин С.С. Физические принципы и структуры электрического дробления шага в дискретном электроприводе // Тр. Моск. энерг. ин-та. 1979. № 440. С. 5-20.
6. Красовский А.Б. Разработка высокочастотного модульного электропривода гибких автоматизированных производств с управляемыми инверторами тока : автореф. дис. … канд. техн. наук. М., МЭИ, 1985. 20 с.
7. Красовский А.Б. Способ управления шаговым двигателем с активным ротором : а.с. 1792226 СССР, МКИ3 Н 02 Р8/00. 2003. 5 с.
8. Ивоботенко Б.А., Ильинский Н.Ф, Копылов И.П. Планирование эксперимента в электромеханике. М.: Энергия, 1978.184 с.
Публикации с ключевыми словами: имитационное моделирование, шаговый двигатель, управляемый инвертор тока, повышение быстродействия, кратковременное повышение фазного тока
Публикации со словами: имитационное моделирование, шаговый двигатель, управляемый инвертор тока, повышение быстродействия, кратковременное повышение фазного тока
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



