научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#8 август 2006
Темпоральное хранилище данных – это хранилище данных с многомерной структурой, имеющее механизмы отслеживания изменений в структуре за счет применения идентификаторов времени валидности, структурных версий и матриц трансформации между структурными версиями [7,8,9].
Темпоральное хранилище состоит из куба данных, элементы которого поддерживают идентификаторы времени валидности. Каждое изменение в структуре измерений многомерной модели порождает создание новой структурной версии. Для сравнения данных двух структурных версий данные одной приводятся к структуре второй.
Для поддержки темпоральности в многомерной структуре данных вводятся следующие понятия:
1. Хрон – обычно одно из измерений в модели определяет время. Мельчайший член измерения «время» является хроном Q. Временная ось определяется через последовательность хронов. Хрон можно определить как «неделимый временной промежуток, фиксированной, минимальной продолжительности»
2. Временной интервал – измерение является последовательностью членов (вершин графа), и иерархических связей между ними (ребра графа), таким образом, полученный граф является деревом, представляющим иерархическую структуру измерения. Чтобы надлежащим образом передать время актуальности такой системы, каждая вершина и ребро графа должны иметь временной интервал ![]() , определяющий время валидности ребра или вершины.
, определяющий время валидности ребра или вершины. ![]() – является началом временного интервала, а
– является началом временного интервала, а ![]() его окончанием.
его окончанием.
Темпорально многомерная система состоит из следующих частей [1,2,3,4]:
1. Количество измерений – ![]() . Если рассматривать факты как измерение, то количество измерений увеличивается на 1 и будет – N+1.
. Если рассматривать факты как измерение, то количество измерений увеличивается на 1 и будет – N+1.
2. Набор измерений:
![]() ,
,
где:
![]() – измерение, представляющее набор анализируемых фактов;
– измерение, представляющее набор анализируемых фактов;
![]() – все оставшиеся измерения, включая измерение «время».
– все оставшиеся измерения, включая измерение «время».
3. Измерение ![]() , определяется как:
, определяется как:
![]() ,
,
где:
![]() , – уникальный идентификатор каждого измерения, который не может быть изменён;
, – уникальный идентификатор каждого измерения, который не может быть изменён;
![]() – уникальный в пределах временного интервала
– уникальный в пределах временного интервала ![]() идентификатор измерения заданный пользователем;
идентификатор измерения заданный пользователем;
![]() (User Defined Attributes) – набор атрибутов, определённых пользователем;
(User Defined Attributes) – набор атрибутов, определённых пользователем;
![]() - время валидности данного члена измерения.
- время валидности данного члена измерения.
4. Количество членов измерений M.
5. Набор членов измерений:
![]() ,
,
где:
![]() – набор всех фактов;
– набор всех фактов;
![]() – набор всех элементов, принадлежащих измерению
– набор всех элементов, принадлежащих измерению ![]() ;
;
6. Член измерения –![]() – член измерения
– член измерения ![]() определяется как:
определяется как:
![]() ,
,
где:
![]() , – уникальный идентификатор каждого члена измерения, который не может быть изменён;
, – уникальный идентификатор каждого члена измерения, который не может быть изменён;
![]() – уникальный в пределах временного интервала
– уникальный в пределах временного интервала ![]() идентификатор члена измерения заданный пользователем;
идентификатор члена измерения заданный пользователем;
![]() -идентификатор измерения к которому принадлежит данный член измерения;
-идентификатор измерения к которому принадлежит данный член измерения;
![]() (User Defined Attributes) – набор атрибутов, определённых пользователем;
(User Defined Attributes) – набор атрибутов, определённых пользователем;
![]() - время валидности данного члена измерения.
- время валидности данного члена измерения.
7. Набор иерархических связей
![]() ,
,
где:
![]() – иерархическая связь
– иерархическая связь
8. Иерархическая связь ![]() , определяется как:
, определяется как:
![]() ,
,
где:
![]() – идентификатор члена измерения;
– идентификатор члена измерения;
![]() – идентификатор элемента измерения, который является родителем для элемента с идентификатором
– идентификатор элемента измерения, который является родителем для элемента с идентификатором ![]() , или пустым множеством, если у элемента с идентификатором
, или пустым множеством, если у элемента с идентификатором ![]() нет родителя;
нет родителя;
![]() , где L – число иерархических уровней в измерении и
, где L – число иерархических уровней в измерении и ![]() – номер уровня на котором располагается элемент с идентификатором
– номер уровня на котором располагается элемент с идентификатором ![]() , все «листья» (элементы не имеющие потомков) в дереве иерархии, расположены на уровне 0;
, все «листья» (элементы не имеющие потомков) в дереве иерархии, расположены на уровне 0;
![]() - время валидности данной иерархической связи между элементами измерения.
- время валидности данной иерархической связи между элементами измерения.
9. Структурная версия SV – это представление многомерной структуры, которая действительна в заданном временном интервале ![]() . Формально структурная версия задаётся следующим образом:
. Формально структурная версия задаётся следующим образом:
![]() ,
,
где:
![]() – уникальный идентификатор структурной версии;
– уникальный идентификатор структурной версии;
![]() – временной интервал в течение которого данная структурная версия действительна;
– временной интервал в течение которого данная структурная версия действительна;
![]() – набор элементов измерения
– набор элементов измерения ![]() , которые действительны в каждой точке временного интервале описываемой структурной версии;
, которые действительны в каждой точке временного интервале описываемой структурной версии;
![]() – набор фактов, которые действительны в каждой точке временного интервала описываемой структурной версии;
– набор фактов, которые действительны в каждой точке временного интервала описываемой структурной версии;
![]() – набор иерархических связей, которые действительны в каждой точке временного интервала, описываемой структурной версии. На концептуальном уровне (не на уровне реализации) можно сказать, что каждой структурной версии соответствует свой куб данных.
– набор иерархических связей, которые действительны в каждой точке временного интервала, описываемой структурной версии. На концептуальном уровне (не на уровне реализации) можно сказать, что каждой структурной версии соответствует свой куб данных.
10. Хранилище данных DWH есть непустое конечное множество структурных версий:
![]()
Для описания статической структуры модели темпорально-многомерного хранилища данных в терминологии классов объектно-ориентированного программирования используем диаграммы классов в нотации языка UML [10]. Диаграмма представлена на Рис. 1.
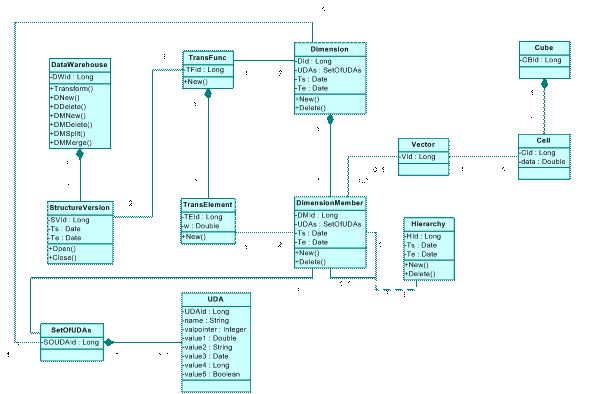
Рис. 1. Объектно-реляционная модель темпорального хранилища данных
Для формирования связей между структурными версиями предлагается использовать матрицы трансформации.
![]() – матрица трансформации измерения
– матрица трансформации измерения ![]() в измерение
в измерение ![]() при отображении куба данных структурной версии
при отображении куба данных структурной версии ![]() в структуру структурной версии
в структуру структурной версии ![]() . Матрица строится следующим образом,– по вертикали откладываются элементы измерения
. Матрица строится следующим образом,– по вертикали откладываются элементы измерения ![]() , а по горизонтали элементы
, а по горизонтали элементы ![]() на пересечении выставляются коэффициенты трансформации –
на пересечении выставляются коэффициенты трансформации – ![]() ;
;
![]() – куб в структурной версии
– куб в структурной версии ![]() ;
;
![]() – куб в структурной версии
– куб в структурной версии ![]() ;
;
![]() – куб
– куб ![]() в структурной версии
в структурной версии ![]() ;
;
![]() – куб
– куб ![]() в структурной версии
в структурной версии ![]() ;
;
![]() – двумерная матрица, представляющая собой развёртку куба данных
– двумерная матрица, представляющая собой развёртку куба данных ![]() , такую, что по горизонтали располагаются элементы
, такую, что по горизонтали располагаются элементы ![]() , а по вертикали все возможные комбинации элементов остальных измерений;
, а по вертикали все возможные комбинации элементов остальных измерений;
![]() – двумерная матрица представляющая собой развёртку куба данных
– двумерная матрица представляющая собой развёртку куба данных ![]() , такую, что по горизонтали располагаются элементы
, такую, что по горизонтали располагаются элементы ![]() , а по вертикали все возможные комбинации элементов остальных измерений; тогда, можно определить следующую формулу:
, а по вертикали все возможные комбинации элементов остальных измерений; тогда, можно определить следующую формулу:
![]()
Операция перемножения в данной формуле означает обычное перемножение матриц (так при перемножении ![]() на
на ![]() получаем
получаем ![]() ;
; ![]() – количество комбинаций членов измерений без
– количество комбинаций членов измерений без ![]() ,
, ![]() -количество элементов
-количество элементов ![]() ,
, ![]() -количество элементов измерения
-количество элементов измерения ![]() ).
).
Возможны следующие варианты:
![]() – перегруппировка мощности элементов измерения;
– перегруппировка мощности элементов измерения;
![]() – объединение элементов измерения;
– объединение элементов измерения;
![]() – дробление элементов измерения;
– дробление элементов измерения;
![]() – порождение нового измерения с k элементами;
– порождение нового измерения с k элементами;
![]() – вырождение одного измерения (в частном случае – агрегация).
– вырождение одного измерения (в частном случае – агрегация).
Для преобразования всего куба необходимо произвести поочерёдное перемножение разверток куба по измерениям на соответствующие матрицы преобразования этих измерений.
Преобразование всего куба данных ![]() в
в ![]() можно описать следующей формулой:
можно описать следующей формулой:
где:
N– количество различных измерений двух структурных версий, то есть если ![]() и
и ![]() количество измерений в структурных версиях
количество измерений в структурных версиях ![]() и
и ![]() , то
, то ![]() ;
;
Обобщённый алгоритм трансформации хранилища данных из одной структурной версии в другую представлен на Рис. 2, данный алгоритм представляет собой реализацию формулы (1).

Рис. 2. Алгоритм трансформации куба данных
Приведенное формальное описание трансформации хранилища данных предполагает перемножение матриц трансформации (сложность алгоритма перемножения матриц – ![]() ) на двумерное представление многомерного куба данных что в условиях наличия большого количества измерений является достаточно ёмкой операцией, как по использованию оперативной памяти системы, так и процессорного времени. Важной особенностью кубов данных является наличие большого количества нулевых элементов – разреженность куба данных, что ведёт к нерациональному расходу памяти при представлении матриц в виде двумерных массивов. Матрицы трансформации также отличаются наличием большой доли нулевых элементов. Проведено исследование алгоритмов перемножения матриц и вариантов представления их в программе и, с учётом описанных особенностей, предлагается оптимизированное для решаемой задачи представление матриц в виде массива связных списков и алгоритм трансформации куба данных с представлением куба данных и матриц трансформации в виде массива связных списков [5,6].
) на двумерное представление многомерного куба данных что в условиях наличия большого количества измерений является достаточно ёмкой операцией, как по использованию оперативной памяти системы, так и процессорного времени. Важной особенностью кубов данных является наличие большого количества нулевых элементов – разреженность куба данных, что ведёт к нерациональному расходу памяти при представлении матриц в виде двумерных массивов. Матрицы трансформации также отличаются наличием большой доли нулевых элементов. Проведено исследование алгоритмов перемножения матриц и вариантов представления их в программе и, с учётом описанных особенностей, предлагается оптимизированное для решаемой задачи представление матриц в виде массива связных списков и алгоритм трансформации куба данных с представлением куба данных и матриц трансформации в виде массива связных списков [5,6].
Так матрица A, которая при представлении в виде двумерного массива выглядит как:
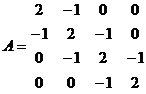
Та же матрица при представлении в виде массива списков примет вид:

Для перемножения матрицы, представляющей двумерную развёртку куба ![]() на матрицу трансформации
на матрицу трансформации ![]() , если использовать классическое представление матриц в виде двумерных массивов, должна получиться матрица
, если использовать классическое представление матриц в виде двумерных массивов, должна получиться матрица ![]()
При представлении матриц в виде векторов списков примем следующие обозначения:
1. Матрицу ![]() будем представлять в виде вектора длины
будем представлять в виде вектора длины ![]() содержащего в качестве элементов списки пар {индекс; элемент}, каждый список может содержать не более
содержащего в качестве элементов списки пар {индекс; элемент}, каждый список может содержать не более ![]() пар. Обозначим этот вектор как
пар. Обозначим этот вектор как ![]() .
.
2. Матрицу ![]() транспонируем и получим
транспонируем и получим ![]() . Представим результат в виде вектора длины
. Представим результат в виде вектора длины ![]() содержащего в качестве элементов списки пар {индекс; элемент}, каждый список может содержать не более
содержащего в качестве элементов списки пар {индекс; элемент}, каждый список может содержать не более ![]() пар. Обозначим этот вектор как
пар. Обозначим этот вектор как ![]() .
.
3. Результатом перемножения матрицы ![]() на матрицу
на матрицу ![]() будет матрица
будет матрица ![]() .
.
В алгоритме примем следующие обозначения:
1. Пары {индекс; элемент} будут представляться как объект IndexElement;
2. ![]() , как Vector[] a – массив списков, содержащих объекты IndexElement;
, как Vector[] a – массив списков, содержащих объекты IndexElement;
3. ![]() , как Vector[] b – массив списков, содержащих объекты IndexElement;
, как Vector[] b – массив списков, содержащих объекты IndexElement;
4. ![]() , как Vector[] с – массив списков, содержащих объекты IndexElement;
, как Vector[] с – массив списков, содержащих объекты IndexElement;
Алгоритм перемножения разреженных матриц приведён на Рис. 3.

Рис. 3. Алгоритм перемножения разреженных матриц
В связи с важностью процесса внедрения нового темпорального хранилища без потери данных, накопленных в старых многомерных и реляционных хранилищах данных, рассматривается вопрос перехода на темпорально многомерное хранилища данных [12,13]. Приводится алгоритм перехода с существующих систем хранения информации на темпоральное хранилище данных с формированием матриц трансформации, которые обеспечивают возможность вовлечения в анализ старых данных одновременно с новыми данными. Алгоритм представлен на Рис. 4.

Рис. 4. Алгоритм перехода с существующих систем хранения многомерной информации на темпоральное хранилище данных
Механизм матриц трансформации возможно применить и в ETL процессе при преобразовании данных исходной системы в структуру хранилища данных [11,14,15]. Алгоритм ETL процесса с использованием матриц трансформации представлен на Рис. 5.

Рис. 5. Алгоритм ETL процесса с использованием матриц транформации
Данный алгоритм состоит из двух частей: действий, которые выполняются регулярно при загрузке данных из оперативной регистрирующей системы и действий, которые выполняются однократно, на этапе определения правил трансформации данных.
Описаное ETL-взаимодействие успешно используется и подтвердило верность теоретических исследований практическими результатами.
Описанные в статье алгоритмы позволяют обеспечить полный цикл функционирования темпорального хранилища данных. Доказана возможность реализации основных процедур темпорального хранилища данных на основе применения механизма матриц трансформации.
ЛИТЕРАТУРА
1. Спандерашвили Д.В. Механизмы отслеживания изменений в многомерных структурах данных // Инфокоммуникационные технологии в науке и технике: Материалы международной научно-технической конференции. Ставрополь: СКГТУ, 2006. Ч 1. С. 160-162.
2. Спандерашвили Д.В. Объектная модель Темпорально многомерных данных и ее реализация средствами реляционной СУБД // Известия ОГТУ. Информационные системы и технологии. Орел, 2006. №1. Т 4. С 210-215.
3. Спандерашвили Д.В. Особенности построения системы сбора статистики телекоммуникационной компании // Информатика: проблемы, методология, технологии: Материалы региональной научно-методической конференции. Воронеж: ВГУ, 2005. Ч 2. С. 136-141.
4. Спандерашвили Д.В. Темпорально многомерная модель для контроля динамики данных региональной компании // Проблемы стратегии регионального развития: Материалы всероссийской научной конференции. Тамбов: ТГУ, 2006. С. 80-84.
5. Д.Кнут . Искусство программирования . Вильямс, 2000.
6. Кормен Т. . Алгогритмы, построение и анализ . Вильямс, 2005
7. P. Chamoni and S. Stock . Temporal Structures in Data Warehouse . Data Warehousing and knowladge discovery, 1999, pp. 353-358
8. E.F. Codd, S.B. Codd, C.T. Salley . Providing OLAP (On-Line Analytical Processing) to User-Analysts: An IT Mandate . E.F.Codd & Associates, 1993.
9. C.S. Jensen C.E. Dyreson . Glossary of Temporal Database Concepts . Springer-Verlag A consensus, 1998, pp. 367-405.
10. Donald Bell . UML basics . IBM Corporation 2003.
11. Ralph Kimball, Joe Caserta . The Data Warehouse ETL Toolkit . Wiley Press, 2004.
12. A. Kurz . Data Warehousing-Enabling Tachnology . MITP-Verlag . Bonn, 1999.
13. C. Liu X.Wang . A Data Model for Supporting On-Line Analytical Processing . ACM, CIKM, 1996
14. Eric Thomsen . OLAP Solutions: Building Multidimensional Information Systems . John Wiley, 1997.
15. P. Vassiliadis, T.Sellis . A Survey of Logical Models for OLAP Databases . SIGMOD records, 1999
Публикации с ключевыми словами: OLAP, разреженные матрицы, ETL-процесс, хранилище данных, Темпоральное хранилище данных, алгоритм перемножения матриц
Публикации со словами: OLAP, разреженные матрицы, ETL-процесс, хранилище данных, Темпоральное хранилище данных, алгоритм перемножения матриц
Смотри также:
- ПРИНЦИПЫ ОРГАНИЗАЦИИ ВЗАИМОДЕЙСТВИЯ РЕГИСТРИРУЮЩИХ СИСТЕМ С ХРАНИЛИЩЕМ ДАННЫХ (НА ПРИМЕРЕ ТЕЛЕКОММУНИКАЦИОННОЙ КОМПАНИИ)
- Автоматизация процесса проведения смотров академической успеваемости студентов вуза
- Методы улучшения комплекса бизнес-процессов по предоставлению, учету и анализу услуг широкополосного доступа в Интернет в телекоммуникационных компаниях
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



