научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#6 июнь 2006
РЕАЛИЗАЦИЯ ФИЛЬТРА ВОЛЬТЕРРА ВТОРОГО ПОРЯДКА ДЛЯ ИДЕНТИФИКАЦИИ НЕЛИНЕЙНЫХ СИСТЕМ управления
К.А.Пупков, Т.Ю.Цибизова
д.т.н., профессор, к.ф.н., доцент
МГТУ им. Н.Э.Баумана
Работа посвящена проблеме идентификации нелинейных систем. В качестве основной трудности данной проблемы можно назвать необходимость обработки большой базы данных, характеризующей работу идентифицируемой системы. Конструктивным подходом в решении данной задачи является использование фильтрующей структуры в виде последовательности Вольтерра. Однако одной из главных причин достаточно редкого применения методики фильтрации Вольтерра на практике является значительная сложность, связанная с реализацией фильтров Вольтерра. Таким образом, главной задачей является нахождение упрощений в разработке и реализации фильтра Вольтерра.
Теория идентификации нелинейных систем, впервые сформулированная в начале XX века, применима для широкого круга нелинейных задач, описывающих большинство сложных процессов. В качестве основной трудности проблемы идентификации можно назвать необходимость обработки большой базы данных, характеризующей работу идентифицируемой системы. Конструктивным подходом в решении данной задачи является использование фильтрующей структуры в виде последовательности Вольтерра. Однако, несмотря на длинную историю и популярность в теоретическом изучении ряда Вольтерра, относительно мало исследователей пытались применить методику фильтрации Вольтерра на практике.
Оказывается, что одна из главных причин - это значительная сложность, связанная с реализацией фильтров Вольтерра. Так как особенная структура фильтра Вольтерра не берется во внимание, то возникают серьезные проблемы с матрицами. Количество операций, необходимое для решения проблемы, увеличивается экспоненциально с увеличением порядка фильтра. Таким образом, главной задачей является нахождение упрощений в разработке и реализации фильтра Вольтерра.
Возьмем фильтр Вольтерра 2-го порядка (ФВ2), который состоит из параллельной комбинации линейного и квадратичного фильтров:
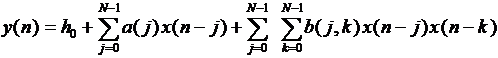 ,
(1)
,
(1)
где {a(j)} и {b(j,k)} называются линейным и квадратичным весом соответственно, а N указывает длину фильтра (предполагается симметричность квадратичных весов фильтра, т.е. b(j,k) = b(k,j)).
Требуется минимизировать средне-квадратическую ошибку (СКОШ) между основным сигналом s(n) и выходом фильтра y(n), т.е.
![]() .
(2)
.
(2)
Первым шагом в определении минимума СКОШ фильтра
Вольтерра 2-го порядка является требование бездрейфового выхода фильтра.
Другими словами, должно быть E[y(n)] = 0, т.к. основной
сигнал имеет нулевое математическое ожидание. Тогда получается следующее
соотношение между ![]() и
b(j,k):
и
b(j,k):
 ,
(3)
,
(3)
где
![]() (4)
(4)
обозначает автокорреляционную функцию x(n).
Следовательно, формула для определения ФВ2 будет выглядеть так:
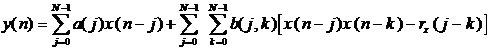 .
(5)
.
(5)
Следующий шаг - определение линейного и квадратичного весов фильтра, которые определяют минимум СКОШ. Для этого выведем простое решение для оптимального ФВ2 в предположении, что на входе фильтра белый гауссовый шум.
Формулу (5) можно переписать в матричном виде:
![]() {
{![]() },
(6)
},
(6)
где
![]() ,
,
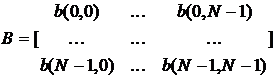 ,
,
а ![]() указывает на NxN
матрицу от x(n), где
указывает на NxN
матрицу от x(n), где ![]() - автокорреляционная функция входного
сигнала x(n). А и В - операторы линейного и квадратичного
фильтра соответственно.
- автокорреляционная функция входного
сигнала x(n). А и В - операторы линейного и квадратичного
фильтра соответственно.
Определим кросс-корреляционную ![]() и кросс-бикорреляционную
и кросс-бикорреляционную ![]() функции между x(n)
и s(n) следующим образом:
функции между x(n)
и s(n) следующим образом:
![]()
или в матричном виде:
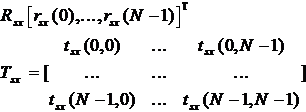
Итак, из (2) видно, что линейный и квадратичный операторы ФВ2 с минимальной СКОШ должны удовлетворять следующим математическим соотношениям:
![]() (7)
(7)
и
![]() (8)
(8)
После некоторых преобразований получается, что линейный и квадратичный операторы фильтра определяются следующим образом:
![]() (9)
(9)
Отсюда видно, что линейный оператор оптимального ФВ2 - это то же самое, что и оптимальный линейный фильтр. Следовательно, можно сконструировать фильтр просто посредством добавления квадратичного фильтра параллельно созданному линейному фильтру.
Предлагается два класса реализации квадратичного оператора ФВ2.
Класс I (умножитель + линейный фильтр)

Рис. 1.
Класс II (линейные фильтры + умножитель)
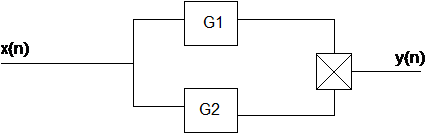
Рис. 2.
Квадратичный фильтр класса I имеет вид:
 .
(10)
.
(10)
Как видно из рис. 1 фильтр состоит из умножителя и
следующего за ним линейного фильтра. такая реализация также соответствует
случаю, когда квадратичный оператор фильтра диагональный, т.е. b(j,k)=0
для ![]() .
.
Здесь СКОШ минимизируется с помощью
![]() ,
,
где
![]()
и ![]() - матрица размера NxN,
которой (j,k)-й элемент равен
- матрица размера NxN,
которой (j,k)-й элемент равен ![]() . В данном случае СКОШ квадратичного фильтра
представляется в виде:
. В данном случае СКОШ квадратичного фильтра
представляется в виде:
![]() .
.
Квадратичный фильтр класса II имеет вид:
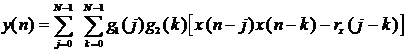 .
(11)
.
(11)
Таким образом это соответствует случаю, когда оператор квадратичного фильтра может быть разложен на два линейных фильтра:
![]() .
.
Следовательно, как показано на рис. 2, фильтр состоит из параллельной комбинации двух фильтров, чьи выходные значения перемножаются для получения выходного значения всего фильтра, и может быть записан в виде:
![]() ,
(12)
,
(12)
где
![]() .
.
Тогда СКОШ между выходом фильтра и значением s(n)
выражается через ![]() и
и
![]() :
:
![]() .
.
Следующим шагом должна быть минимизация по ![]() . Однако одновременная
минимизация по 2N переменным представляет собой потенциальную
вычислительную проблему из-за связи между
. Однако одновременная
минимизация по 2N переменным представляет собой потенциальную
вычислительную проблему из-за связи между ![]() и
и ![]() . В качестве альтернативы одновременной
минимизации предлагается методика последовательных итераций:
. В качестве альтернативы одновременной
минимизации предлагается методика последовательных итераций:
Шаг
1: произвольно выбрать первый
линейный фильтр ![]() с
с
![]() .
.
Шаг
2: с выбранным ![]() определить
определить ![]() по формуле
по формуле ![]() ,
,
где
![]() .
.
Шаг
3: с выбранным ![]() , используя формулу
, используя формулу ![]() , где
, где
![]() , определить
, определить ![]() .
.
Шаг 4: повторять шаги 2 и 3 до тех пор, пока значение минимизированной СКОШ не станет пренебрежительно мало.
Список литературы:
1. Пупков К.А., Капалин В.И., Ющенко А.С. Функциональные ряды в теории нелинейных систем. - М: Наука, 1976. - 448 с.
2. Taiho Koh, Edward J.Powers, Second-Order Volterra Filtering and its Application to Non-Linear System Identification, 1985 IEEE.
Публикации с ключевыми словами: нелинейные системы
Публикации со словами: нелинейные системы
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



