научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 08, август 2013
DOI: 10.7463/0813.0586737
УДК 311.17
Россия, МГТУ им. Н.Э. Баумана
Введение
Пусть в последовательности независимых испытаний вероятность события ![]() равна,
равна, ![]() причем,
причем, ![]() . Тогда между функциями распределения биномиального и нормального законов
. Тогда между функциями распределения биномиального и нормального законов
![]() и
и 
существует следующая связь (интегральная теорема Муавра-Лапласа) [1]:
![]() ,
,
где ![]() - число сочетаний из n элементов по k, q=1-p.
- число сочетаний из n элементов по k, q=1-p.
Для построения статистических проверок гипотез с заданными вероятностями ошибок требуется информация о значениях «хвостов» распределений. Однако, относительная погрешность нормальной аппроксимации биномиального распределения на его «хвостах» довольно велика [2]. Это послужило одной из причин разработки теории больших уклонений, доказательства различных неравенств «хвостов» биномиального закона, а также для «хвостов» распределения сумм случайных величин [3].
В качестве примеров можно указать экспоненциальную оценку «хвостов» для сумм ![]() независимых случайных величин
независимых случайных величин ![]() со значениями из отрезка [0,1], которую получил В. Хёвдинг [4]: если
со значениями из отрезка [0,1], которую получил В. Хёвдинг [4]: если ![]() , (здесь
, (здесь ![]() - обозначение математического ожидания), то
- обозначение математического ожидания), то
![]() ,
,
где ![]() - произвольное число,
- произвольное число, ![]() - обозначение вероятности, а также формулу Пуассона [1] при малых p:
- обозначение вероятности, а также формулу Пуассона [1] при малых p:
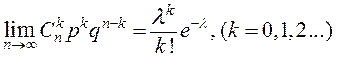 ,
,
где ![]() - постоянная.
- постоянная.
Заметим, что это предельное соотношение послужило основой математической модели пуассоновского потока отказов в теории надёжности, выраженной следующей формулой для вероятности появления k отказов за время длительностью t:
 .
.
В частности, при k = 0 из этого соотношения находим формулу для вероятности безотказной работы объекта в течение времени t
![]() ,
,
где ![]() - заданная (постоянная) интенсивность отказов.
- заданная (постоянная) интенсивность отказов.
1. Постановка задачи
В системе управления надежностью часто возникает вопрос о соответствии интенсивности отказов определенного типа комплектующих изделий (КИ) среднему значению интенсивности отказов для группы КИ разных типов, объединенных по принципу единства технологии изготовления, назначения и условий их эксплуатации. Для решения этого вопроса обычного сравнения точечных оценок интенсивностей отказов группы типов КИ по ряду причин недостаточно. В связи с этим возникает задача статистической проверки, так называемой, нулевой гипотезы о соответствии интенсивности отказов типа среднегрупповому значению интенсивности отказов в случае пуассоновского процесса.
2. Основное утверждение
Допустим, что группу образует ![]() типов КИ. Пусть наработка
типов КИ. Пусть наработка ![]() -го типа составила
-го типа составила ![]() часов, а число отказов в количестве
часов, а число отказов в количестве ![]() . Через
. Через ![]() (
(![]() ) обозначим случайное число отказов, а через
) обозначим случайное число отказов, а через ![]() - наблюденное число.
- наблюденное число.
Общая наработка группы типов КИ при этом составит
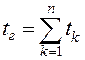 .
.
Пусть ![]() - интенсивность отказов
- интенсивность отказов ![]() -го типа КИ.
-го типа КИ.
Тогда для пуассоновской случайной величины  имеем
имеем
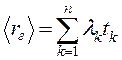 , (1)
, (1)
так как
![]() ,
,
где ![]() - математическое ожидание величины, стоящей внутри угловых скобок.
- математическое ожидание величины, стоящей внутри угловых скобок.
С другой стороны,
![]() . (2)
. (2)
Из соотношений (1) и (2) найдем
 ,
,
где ![]() и
и ![]() постоянны.
постоянны.
Пусть имеются основания предполагать, что неизвестная интенсивность отказов ![]() -го типа КИ
-го типа КИ ![]() (
(![]() ) равна среднегрупповой интенсивности отказов
) равна среднегрупповой интенсивности отказов ![]() , которая в свою очередь тоже неизвестна, т. е. определим нулевую гипотезу
, которая в свою очередь тоже неизвестна, т. е. определим нулевую гипотезу
![]() (3)
(3)
и займемся построением решающего правила ее проверки при наблюдаемом числе отказов ![]() и
и ![]() и соответствующих наработках
и соответствующих наработках ![]() и
и ![]() .
.
Для этой цели нам необходимо доказать следующее утверждение
Теорема. При условии нулевой гипотезы (3) справедлива следующая формула:
![]() , (4)
, (4)
где
 , (5)
, (5)
![]() - число сочетаний из
- число сочетаний из ![]() элементов по
элементов по ![]() ;
;
![]() - обозначение условной вероятности события, находящегося в первой скобке относительно события, содержащегося во второй скобке.
- обозначение условной вероятности события, находящегося в первой скобке относительно события, содержащегося во второй скобке.
Доказательство. Из определения пуассоновского потока отказов имеем
 , (6)
, (6)
 (7)
(7)
Рассмотрим следующее условное распределение отказов ![]() -го типа КИ при заданном числе отказов в группе, которое, в силу известных формул из теории вероятностей, равно [1]
-го типа КИ при заданном числе отказов в группе, которое, в силу известных формул из теории вероятностей, равно [1]
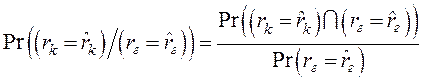 , (8)
, (8)
где ![]() – символ произведения событий, заключенных в скобках.
– символ произведения событий, заключенных в скобках.
Поскольку ![]() и
и ![]() независимые случайные величины, то имеем
независимые случайные величины, то имеем
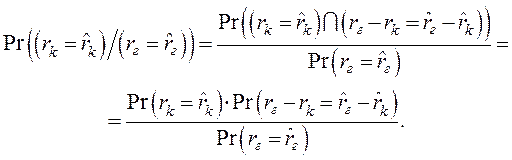 (9)
(9)
Пуассоновская величина ![]() при условии справедливости гипотезы (3) имеет математическое ожидание, равное
при условии справедливости гипотезы (3) имеет математическое ожидание, равное ![]() , поэтому
, поэтому
 . (10)
. (10)
Подставляя соотношения (6), (7) и (10) в (9), получим
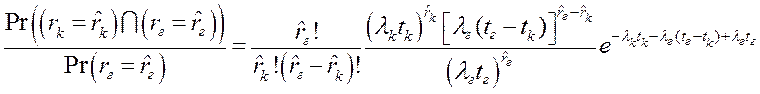 .
.
Откуда, с учетом справедливости гипотезы (3), имеем
 ,
,
где значение ![]() определено формулой (5).
определено формулой (5).
Наконец, подставляя полученное выражение в соотношение (8), получим искомую формулу (4), что и требовалось доказать.
Другими словами, доказанная теорема устанавливает связь условного распределения числа отказов в пуассоновском потоке через биномиальный закон.
В свою очередь, установленная связь позволяет при конкурирующей гипотезе
![]()
в качестве решающего правила определить следующее условие для принятия гипотезы (3):
 , (11)
, (11)
где ![]() - уровень значимости критерия (
- уровень значимости критерия (![]() - мало), а
- мало), а ![]() определено соотношением (5).
определено соотношением (5).
Если же
 , (12)
, (12)
то нулевая гипотеза (3) при конкурирующей ![]() отвергается.
отвергается.
Приведём следующий пример использования проверки гипотезы (3) при конкурирующей гипотезе ![]() .
.
Пример. Наработка ![]() -го типа КИ составила
-го типа КИ составила ![]() , а наработка группы КИ -
, а наработка группы КИ - ![]() . При этом число отказов
. При этом число отказов ![]() -го типа КИ составляет
-го типа КИ составляет ![]() , а для группы
, а для группы ![]() . Требуется проверить нулевую гипотезу
. Требуется проверить нулевую гипотезу ![]() с уровнем значимости
с уровнем значимости ![]() при конкурирующей гипотезе
при конкурирующей гипотезе ![]() .
.
Решение. Воспользуемся решающим правилом в виде (11) или (12). Для этой цели определим величину
 ,
,
которая, после подстановки исходных данных примера, равна
 .
.
Очевидно, что ![]() значительно меньше
значительно меньше ![]() . Следовательно, согласно (12), нулевая гипотеза
. Следовательно, согласно (12), нулевая гипотеза ![]() отвергается.
отвергается.
Заметим, что точечные оценки интенсивностей отказов в условиях примера имеют для ![]() -го типа КИ и группы, соответственно, следующие значения:
-го типа КИ и группы, соответственно, следующие значения:
 ,
,  .
.
Выводы
Таким образом, установлена оценка условного распределения отказов в пуассоновском потоке через биномиальный закон. Установленная оценка позволяет построить новые решающие правила при проверке нулевой гипотезы ![]() .
.
Работа выполнена при поддержке ОАО РТИ им. акад. А.Л. Минца.
Список литературы
1. Гнеденко Б.В., Коваленко И.Н. Введение в теорию массового обслуживания. М.: КомКнига URSS, 2005. 397 c.
2. Зубков А.М., Серов А.А. Незамеченные наилучшие неравенства для биномиального закона // Международная конференция «Теория вероятностей и её приложения» : сб. докл. М.: Ленанд, 2012. С. 35-36.
3. Садыхов Г.С., Савченко В.П. Зависимость показателей ресурса от характеристик его расходования // Доклады РАН. 1998. Т. 361, № 2. С. 189-191.
4. Hoeffding W. Probability inequalities for sums of bounded random variables // J. Amer. Statist. Ass. 1963. Vol. 58, no. 301. P. 13-30.
Публикации с ключевыми словами: интенсивность отказов, нулевая гипотеза, пуассоновский поток отказов, биномиальный закон распределения
Публикации со словами: интенсивность отказов, нулевая гипотеза, пуассоновский поток отказов, биномиальный закон распределения
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



