научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2012
УДК.519.23
МГТУим. Н.Э.Баумана
Введение. Рассмотрим систему, включающую в себя Nосновных рабочих элементов (подсистем), работающих в параллельном нагруженном режиме, при этом предполагается, что эффективность работы системыпропорциональна числуисправно работающих ее элементов. В процессе работы каждый из элементов может отказывать с постоянной функцией интенсивности отказов ![]() где λ – параметр интенсивности отказов одного элемента, другими словами,время безотказной работы (наработка на отказ) каждого отдельного элемента имеет экспоненциальное распределение с функцией надежности
где λ – параметр интенсивности отказов одного элемента, другими словами,время безотказной работы (наработка на отказ) каждого отдельного элемента имеет экспоненциальное распределение с функцией надежности ![]() (см., например, [1] - [3] и др.). При этом предполагается, что отказы различных элементов происходят независимо друг от друга. Аналогичные по смыслу модели надежностирассматривались ранее также в [4] - [6 ] и др.
(см., например, [1] - [3] и др.). При этом предполагается, что отказы различных элементов происходят независимо друг от друга. Аналогичные по смыслу модели надежностирассматривались ранее также в [4] - [6 ] и др.
Обозначим через ![]() момент отказа j-ого элемента,
момент отказа j-ого элемента, ![]()
-индикатор исправной работы j-ого элемента в момент времениtи
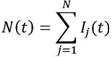
- количество элементов исправно работающих в момент времениt, N(0) = N. Пусть в момент времени ![]() достижения процессом N(t) критического уровня N - rпроисходит остановка работы системы и начинается восстановление (замена)отказавших элементов новымиидентичнымиэлементами, где r- некоторый заданный критический уровень допустимого числа отказов. Восстановление происходит в течение некоторого (вообще говоря, случайного) времени τ, после чего в момент времени
достижения процессом N(t) критического уровня N - rпроисходит остановка работы системы и начинается восстановление (замена)отказавших элементов новымиидентичнымиэлементами, где r- некоторый заданный критический уровень допустимого числа отказов. Восстановление происходит в течение некоторого (вообще говоря, случайного) времени τ, после чего в момент времени ![]() процесс N(t) возвращается в начальное состояние N(0) = N, затемпроцесс работы системы возобновляется, снова продолжается до момента достижения процессом N(t) уровня N - rи т.д.
процесс N(t) возвращается в начальное состояние N(0) = N, затемпроцесс работы системы возобновляется, снова продолжается до момента достижения процессом N(t) уровня N - rи т.д.
Одной из существенных проблем, возникающих в данной ситуации, является выбороптимальногокритического уровня rначала восстановления в системе, который, в свою очередь, задаетоптимальное правило восстановлениядля данной модели.
Нахождение основных характеристик и оптимального уровня начала восстановления в системе.Cреднее значение![]() процесса N(t) на интервале
процесса N(t) на интервале ![]() или, другими словами, среднее число исправно работающих элементовв системе имеет вид
или, другими словами, среднее число исправно работающих элементовв системе имеет вид
| (1) |
где E– символ математического ожидания, ![]() – математическое ожидание указанного выше момента (начала восстановления)
– математическое ожидание указанного выше момента (начала восстановления) ![]() – среднее время восстановления,
– среднее время восстановления, ![]() – средняя длина одного цикла работы системы,
– средняя длина одного цикла работы системы, ![]() – средняя «наработка»(суммарное время работы) всех элементов системы на одном цикле.
– средняя «наработка»(суммарное время работы) всех элементов системы на одном цикле.
Другая существенная характеристика – средние затраты на восстановление элементов системы в единицу времени на интервале ![]() имеет вид
имеет вид
| (2) |
Где β– стоимость восстановления (замены) одного элемента.
Рассмотренный выше процесс N(t) на интервал времени ![]() совпадает с процессом испытаний
совпадает с процессом испытаний![]() идентичных элементов по стандартному плану
идентичных элементов по стандартному плану ![]() (в обозначениях книги [1]).При этом момент начала восстановления
(в обозначениях книги [1]).При этом момент начала восстановления ![]() совпадает с моментом r- ого отказа trили, другими словами, с r - ой порядковой статистикой для выборки объема Nиз экспоненциального распределения с параметром λ ,откуда следует, что математическое ожидание времени начала восстановления(средняя длина цикла)определяется формулой
совпадает с моментом r- ого отказа trили, другими словами, с r - ой порядковой статистикой для выборки объема Nиз экспоненциального распределения с параметром λ ,откуда следует, что математическое ожидание времени начала восстановления(средняя длина цикла)определяется формулой
| (3) |
Суммарное время работы («наработка») элементов на одном цикле имеет вид

где ![]() – последовательные моменты отказов элементов.Эта величинаимеет распределение Эрланга порядка rс параметром λ и математическим ожиданием
– последовательные моменты отказов элементов.Эта величинаимеет распределение Эрланга порядка rс параметром λ и математическим ожиданием
| (4) |
(см., например, [2], [3]). Из (3) и (4) далее следует, что указанные выше основные характеристики – среднее число работающих элементов ![]() и средние затраты
и средние затраты ![]() на восстановление в единицу времени в рамках данной модели имеют вид
на восстановление в единицу времени в рамках данной модели имеют вид
| (5) |
| (6) |
где ![]() – функция от критического уровня rначала восстановления (на каждом цикле), определяемая выражением
– функция от критического уровня rначала восстановления (на каждом цикле), определяемая выражением
| (7) |
В соответствии с (5), (6) при любом критическом уровне начала восстановления rэти характеристики связаны соотношением
| (8) |
где ![]() - математическое ожидание времени безотказной работы (средний ресурс)одного элемента. В соответствии с (8) среднее число исправно работающих элементов в системе пропорционально средним удельным затратам
- математическое ожидание времени безотказной работы (средний ресурс)одного элемента. В соответствии с (8) среднее число исправно работающих элементов в системе пропорционально средним удельным затратам ![]() на восстановление в единицу времени и среднему ресурс у элементов T.
на восстановление в единицу времени и среднему ресурс у элементов T.
Из (7) далее нетрудно получить, что первая разность функции ![]() имеет вид
имеет вид
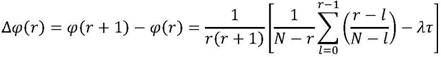
откуда следует, что функция ![]() имеет единственный минимум в точке
имеет единственный минимум в точке
| (9) |
(![]() , если таких rне найдется). Соответственно характеристики
, если таких rне найдется). Соответственно характеристики ![]() имеют в этой точке единственный максимум.
имеют в этой точке единственный максимум.
Поскольку ![]() , то обе характеристики монотонно убывают по r, если выполняется неравенство
, то обе характеристики монотонно убывают по r, если выполняется неравенство
![]()
В этом случае максимальное значение показателя эффективности ![]() достигается при r* = 1 или, другими словами, при наиболее затратном правиле восстановления, когда в случае отказа любого элемента работа системы останавливается и начинается восстановление.
достигается при r* = 1 или, другими словами, при наиболее затратном правиле восстановления, когда в случае отказа любого элемента работа системы останавливается и начинается восстановление.
Если параметры системы удовлетворяют неравенству
![]()
то в этом случае обе указанные выше в (1) , (2)основные характеристики достигают максимального значения при r* > 1, где r* определяется из соотношения (9).
Обозначим далее через ![]() максимально возможное значение показателя эффективности
максимально возможное значение показателя эффективности ![]() . Величину
. Величину
![]()
назовем коэффициентом максимально возможной эффективности (среднего количества исправно работающих элементов) при данных параметрах надежности λи восстановления τ. Для случая N >> 1 из (7), (9)нетрудно далее получить приближенные аналитические выражения
![]()
![]()
откуда видно, что доля заменяемого оборудования ![]() , при которой достигаетсямаксимально возможная эффективность
, при которой достигаетсямаксимально возможная эффективность ![]() , пропорциональна величине
, пропорциональна величине ![]() . При этом указанные относительные характеристики не зависят от общего количества элементов в системе N. Таким образом, основным параметром, определяющим значения основных характеристик системы в рамках данной модели является величина
. При этом указанные относительные характеристики не зависят от общего количества элементов в системе N. Таким образом, основным параметром, определяющим значения основных характеристик системы в рамках данной модели является величина ![]() , гдеT - среднее время безотказной работы (средний ресурс) одного элемента.
, гдеT - среднее время безотказной работы (средний ресурс) одного элемента.
В заключение необходимо отметить, что существенный интерес представляет дальнейшее обобщение полученных результатов на случай более общих распределений времени безотказной работы элементов, а также на более общие модели, учитывающие такие факторы, как возможность «блочных» отказов в системе и др.
Литература
1. Гнеденко Б.В., Беляев Ю.К., Соловьев А.Д.Математические методы в теории надежности.М.: Наука, 1965. – 524 с.
2. Gnedenko B.V., Pavlov I.V., Ushakov I.A.Statistical reliability engineering.N.Y.:John Wiley, 1999,514 p.
3. Горяинов В.Б., Павлов И.В., Тескин О.И.,Цветкова Г.М. Математическая статистика(серия Математика в техническом университете, под редакцией Зарубина В.С., Крищенко А.П., том 17), М.: Изд. МГТУ им. Н.Э. Баумана.-2002. – 424 с.
4. Pavlov I.V., Teskin O.I., Ukolov S.N.A comparison of some exact and approximate methods for calculating confidence bounds for system reliability based on component test data // Proceeding of the first international conference, MMR’97, Bucharest, Romania –Sept., 1997. –pp. 231-236.
5. PavlovI.V., TeskinO.I., GoryainovV.B., UkolovS.N.Confidence bounds for system reliability based on binomial components test data // Proceeding of thesecond international conference, MMR’2000, Bordeaux, France.–Jul., 2000.– pp. 852-855.
6. Лёвин П.А, Павлов И.В., Оценка надежности системы с нагруженным резервированием по результатам испытаний ее элементов //Вестник МГТУ им. Н.Э. Баумана, серия “Естественные Науки”, – 2011, №3, с. 59 - 70.
Публикации с ключевыми словами: надежность, восстановление, интенсивность отказов, средний ресурс элемента
Публикации со словами: надежность, восстановление, интенсивность отказов, средний ресурс элемента
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||