научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#8 август 2006
B. П. Корячко, д-р техн. наук проф.,
C. В. Скворцов, канд. техн. наук доц., Рязанская государственная радиотехническая академия
Иерархическая модель глобальной оптимизации у параллельных объектных программ
Предлагается модель и метод глобальной оптимизации объектного кода для RISC-процессоров с управлением по технологии VLIW, основанные на использовании дизъюнктивных графов информационно-структурных зависимостей.
Введение
Наиболее распространенным подходом к решению задачи синтеза параллельного объектного кода для программ с циклами и ветвлениями является последовательное выделение линейных участков (ЛУ) и синтез командных слов (КС) для каждого ЛУ в отдельности с последующим объединением полученных фрагментов кода [1—4].
Однако результаты исследований [1, 4—7] показывают, что потенциальная возможность параллелизма существует и для операций, принадлежащих разным ЛУ исходной программы. Выявление таких операций проводится методами глобального анализа программ [4, 6, 7], разработка и развитие которых приобретают особую актуальность в связи с распространением RISC-процессоров с управлением параллельным выполнением операций по технологии длинного командного слова (VLIW) [4].
Наиболее известными методами глобального анализа являются планирование трасс [4, 6] и проникающее планирование [4, 7]. Суть этих методов сводится к определению комбинаций ЛУ, операции из которых целесообразно исследовать на возможность параллельного исполнения.
Планирование трасс предполагает предварительное независимое формирование списка КС для каждого ЛУ с последующим определением наиболее вероятных трасс из нескольких последовательных ЛУ и улучшением полученного кода за счет перемещения отдельных операций между этими участками. Наличие условных переходов в пределах одной трассы приводит к необходимости дублирования некоторых перемещенных операций при оптимизации последующих трасс программы.
Проникающее планирование исключает дублирование операций в процессе глобального переупорядочения кода за границами ЛУ и выполняется над моделью программы, которая является обобщением управляющего графа (вершины соответствуют ЛУ, а дуги определяют возможные пути исполнения). Параллелизм в программе выявляется перемещением между вершинами графовой модели условных и безусловных операций. Результатом является преобразованный управляющий граф, обеспечивающий максимальный параллелизм для идеального компьютера, причем для синтеза реального кода требуется выполнить генерацию КС, в которых учитываются ограничения доступа к общим ресурсам процессора.
В работах [8—10]
описана новая формальная модель организации параллельных вычислений на уровне операций
— дизъюнктивный граф информационно-структурных зависимостей Н* = (А,
V, Е). Дуги графа ![]() показывают зависимости по данным, а ребра
показывают зависимости по данным, а ребра ![]() определяют все пары конфликтных операций,
которые не могут быть выполнены параллельно из-за необходимости доступа к общим ресурсам
процессора. Каждый бесконтурный орграф Gi
= (A, Vi),
получаемый в результате замены ребер графа H* дугами,
определяет корректный вариант параллельной объектной программы LW = (LW1, LW2,
..., LWN), в которой каждое командное слово
определяют все пары конфликтных операций,
которые не могут быть выполнены параллельно из-за необходимости доступа к общим ресурсам
процессора. Каждый бесконтурный орграф Gi
= (A, Vi),
получаемый в результате замены ребер графа H* дугами,
определяет корректный вариант параллельной объектной программы LW = (LW1, LW2,
..., LWN), в которой каждое командное слово
![]() составляют операции
составляют операции ![]() , расположенные на одном ярусе графа
Gi. Орграф Gi*
= (A, Vi*)
с минимальной длиной критического пути соответствует объектной программе, исполняемой
за минимальное время [8, 10].
, расположенные на одном ярусе графа
Gi. Орграф Gi*
= (A, Vi*)
с минимальной длиной критического пути соответствует объектной программе, исполняемой
за минимальное время [8, 10].
Анализ свойств дизъюнктивных графов информационно-структурных зависимостей [8, 9] позволяет предложить на их основе оригинальный подход к глобальной оптимизации объектного кода, не требующий предварительного синтеза КС для всех ЛУ в отдельности (ограничиваясь выделением циклических участков и альтернативных ветвей) и сочетающий преимущества обоих указанных выше методов, а именно:
· глобальное преобразование кода достигается перемещением операций программы между различными ЛУ;
· отсутствует дублирование операций исходной программы;
· учитываются ограничения архитектуры процессора.
Иерархическая графовая модель программы
Предположим, что
в процессе трансляции исходная программа преобразована в последовательность А
= (а1, a2,..., аn) операций, представленных в стандартной машинно-независимой
тетрадной форме [11] вида ![]() ,
которая определяет тип Ci операнды
,
которая определяет тип Ci операнды ![]() и результат Oi
производимой операции, причем для организации ветвлений и циклов могут использоваться
следующие операции: безусловного перехода (jm,,,
ak) на операцию
и результат Oi
производимой операции, причем для организации ветвлений и циклов могут использоваться
следующие операции: безусловного перехода (jm,,,
ak) на операцию ![]() , где k > i
или k < i; условных
переходов к выполнению операции
, где k > i
или k < i; условных
переходов к выполнению операции ![]() (k > i или k
< i) по нулевому (jmz,
X, , ak),
положительному (jmp, X,
, ak), отрицательному (jmn,
X, , ak)
и другим значениям операнда X.
(k > i или k
< i) по нулевому (jmz,
X, , ak),
положительному (jmp, X,
, ak), отрицательному (jmn,
X, , ak)
и другим значениям операнда X.
Информационная
зависимость операций ![]() порождает
биологический граф программы [12, 13], адекватно описывающий структуру исходной программы
A на микроуровне параллелизма и представляющий собой
орграф Gб = (А, Vб),
вершины которого соответствуют операциям
порождает
биологический граф программы [12, 13], адекватно описывающий структуру исходной программы
A на микроуровне параллелизма и представляющий собой
орграф Gб = (А, Vб),
вершины которого соответствуют операциям ![]() ,
а дуги задают связи по данным и управлению.
,
а дуги задают связи по данным и управлению.
Для вершин Gб с помощью логических функций И и ИСКЛЮЧАЮЩЕЕ
ИЛИ (ИСКЛ. ИЛИ) определены условия входа и выхода, которые описывают логику программы,
т. е. каждой вершине сопоставлена одна из пар вида (&, &), (&, ![]() ), (
), (![]() , &) или (
, &) или (![]() ,
,![]() ), что определяет разбиение
), что определяет разбиение ![]() , где первый индекс показывает тип входной,
а второй — выходной логики для вершин каждого подмножества.
, где первый индекс показывает тип входной,
а второй — выходной логики для вершин каждого подмножества.
В корректной билогической
модели [13] вершина ![]() может
иметь выходную функцию ИСКЛ. ИЛИ только при |Г(ai)|
= 2 (условный переход для выбора одной из альтернативных ветвей или выход из цикла
с постусловием) и вершина
может
иметь выходную функцию ИСКЛ. ИЛИ только при |Г(ai)|
= 2 (условный переход для выбора одной из альтернативных ветвей или выход из цикла
с постусловием) и вершина ![]() —
входную функцию ИСКЛ. ИЛИ только для |Г-1(ai)|
= 2, что определяет точку схождения двух ветвей или входа в цикл. При необходимости
это достигается введением дополнительных вершин
—
входную функцию ИСКЛ. ИЛИ только для |Г-1(ai)|
= 2, что определяет точку схождения двух ветвей или входа в цикл. При необходимости
это достигается введением дополнительных вершин ![]() с логикой И, которые определяют фиктивные операции входа и выхода
для соответствующих альтернативных и циклических фрагментов программы.
с логикой И, которые определяют фиктивные операции входа и выхода
для соответствующих альтернативных и циклических фрагментов программы.
Граф Gб
= (А, Vб) позволяет выполнить глобальный
анализ структуры (логики) программы, но не учитывает ограничений на параллелизм операций
из-за конфликтов по ресурсам. Поэтому предлагается использовать билогическую модель
Gб в качестве источника свойств глобального
параллелизма операций, необходимых для построения иерархической графовой модели H** = (А*, V*, Е*)
синтеза параллельного объектного кода с циклами и ветвлениями на основе ![]() множеств
множеств ![]() вложенных дизъюнктивных графов
вложенных дизъюнктивных графов ![]() информационно-структурных зависимостей, отражающих возможные
варианты конфликтов операций на каждом p-м уровне иерархии
информационно-структурных зависимостей, отражающих возможные
варианты конфликтов операций на каждом p-м уровне иерархии
![]() .
.
Для каждого значения
p < p* число элементов
множества Mp определяется числом циклических
и альтернативных ветвей равного уровня вложенности, а множество ![]() всегда содержит только один элемент, который
описывает иерархическую модель H** = (A*,
V*, E*), где
всегда содержит только один элемент, который
описывает иерархическую модель H** = (A*,
V*, E*), где ![]() .
.
Построение модели
Н** осуществляется посредством эквивалентных, с точки зрения семантики программы,
преобразований билогического графа, начиная с низшего (p
= 0) уровня иерархии, для которого ![]() ,
где
,
где ![]() и
и ![]() . Переход на более высокий (p
+ 1)-й уровень иерархии означает частичное исключение циклов и ветвлений [12], а
следовательно, сокращение общего числа вершин
. Переход на более высокий (p
+ 1)-й уровень иерархии означает частичное исключение циклов и ветвлений [12], а
следовательно, сокращение общего числа вершин ![]() логикой ИСКЛ. ИЛИ в графовой модели
логикой ИСКЛ. ИЛИ в графовой модели ![]() .
.
Для этого в текущей
билогической модели ![]() выделяются
ориентированные подграфы
выделяются
ориентированные подграфы ![]() , которые описывают циклические и альтернативные фрагменты,
содержащие только вершины
, которые описывают циклические и альтернативные фрагменты,
содержащие только вершины ![]() ,
где
,
где ![]() . На их основе строятся
дизъюнктивные подграфы
. На их основе строятся
дизъюнктивные подграфы ![]() и
далее
и
далее ![]() , где
, где ![]() и
и ![]() которые затем заменяются макровершинами типа
которые затем заменяются макровершинами типа ![]() или
или ![]() в соответствии со схемами, показанными на рис. 1 и 2.
в соответствии со схемами, показанными на рис. 1 и 2.
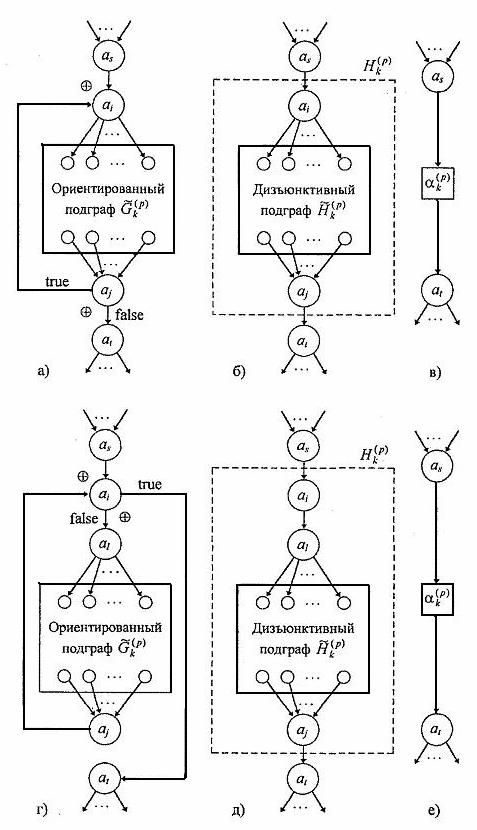
Рис. 1. Преобразование циклических фрагментов:
а — цикл с постусловием в билогической модели; б — дизъюнктивный подграф p-го уровня иерархии для цикла с постусловием; в — результат стягивания цикла с постусловием; г — цикл с предусловием в исходной билогической модели; д — дизъюнктивный подграф p-гo уровня для цикла с предусловием; е — результат стягивания цикла с предусловием
Схемы стягивания циклических фрагментов
билогической модели в вершины ![]() показаны
на рис. 1. Структура исходного цикла с постусловием выхода представлена на рис. 1,
а, где символом
показаны
на рис. 1. Структура исходного цикла с постусловием выхода представлена на рис. 1,
а, где символом ![]() явно
указана логика вершин ИСКЛ. ИЛИ (
явно
указана логика вершин ИСКЛ. ИЛИ (![]() — точка входа,
— точка входа, ![]() —
точка выхода из цикла), а подграф
—
точка выхода из цикла), а подграф ![]() ,
описывающий тело цикла, условно изображен прямоугольником. Рис. 1, б иллюстрирует
преобразование графовой модели в целях исключения логики ИСКЛ. ИЛИ и получения дизъюнктивного
графа
,
описывающий тело цикла, условно изображен прямоугольником. Рис. 1, б иллюстрирует
преобразование графовой модели в целях исключения логики ИСКЛ. ИЛИ и получения дизъюнктивного
графа ![]() , ограниченного штриховой
линией. Конечный результат преобразования циклического фрагмента билогического графа
с постусловием выхода показан на рис. 1, в. Преобразование циклической структуры
с предусловием выхода показано на рис. 1, г— 1, е, где
, ограниченного штриховой
линией. Конечный результат преобразования циклического фрагмента билогического графа
с постусловием выхода показан на рис. 1, в. Преобразование циклической структуры
с предусловием выхода показано на рис. 1, г— 1, е, где ![]() — точка входа и выхода одновременно,
причем вершина
— точка входа и выхода одновременно,
причем вершина ![]() может
соответствовать фиктивной операции, которая введена, чтобы обеспечить выполнение
условий корректности билогической модели программы [11].
может
соответствовать фиктивной операции, которая введена, чтобы обеспечить выполнение
условий корректности билогической модели программы [11].
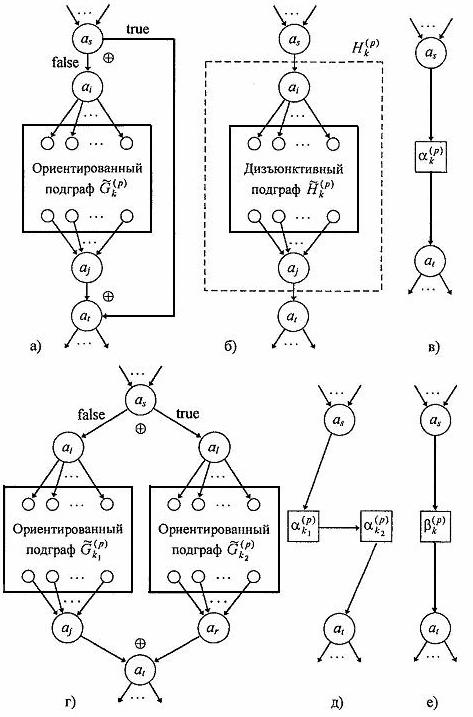
Рис. 2. Преобразование условных и альтернативных ветвей:
а — условная ветвь программы в билогической модели; б — дизъюнктивный подграф p-го уровня иерархии для условной ветви; в — результат стягивания условной ветви; г — альтернативные ветви в билогической модели; д — результат стягивания альтернативных ветвей; e — составная макровершина иерархического дизъюнктивного графа
Условная ветвь
программы (рис. 2, а—2, в), которой соответствует дизъюнктивный граф
![]() , стягивается в одну вершину
типа
, стягивается в одну вершину
типа ![]() . Пара вершин
. Пара вершин ![]() и
и ![]() , описывающая альтернативные ветви программы, заменяется составной
макровершиной
, описывающая альтернативные ветви программы, заменяется составной
макровершиной ![]() , как это показано
на рис. 2, г—2, е, где ветвь
, как это показано
на рис. 2, г—2, е, где ветвь ![]() выполняется при истинном (true), a
выполняется при истинном (true), a ![]() — при ложном (false) результате
проверки условия перехода.
— при ложном (false) результате
проверки условия перехода.
Затем каждая вершина ![]() или
или ![]() включается в с соответствующей корректировкой
включается в с соответствующей корректировкой ![]() и далее рассматривается как макрооперация,
блокирующая доступ к любым ресурсам процессора на период Т(
и далее рассматривается как макрооперация,
блокирующая доступ к любым ресурсам процессора на период Т(![]() ) или
) или ![]() ,
длительность которого определяется временем однократного исполнения (в тактах) сформированной
последовательности КС, которую будем называть макрокомандой, для циклического или
альтернативного фрагмента объектной программы.
,
длительность которого определяется временем однократного исполнения (в тактах) сформированной
последовательности КС, которую будем называть макрокомандой, для циклического или
альтернативного фрагмента объектной программы.
Если полученный
билогический граф ![]() удовлетворяет
условию
удовлетворяет
условию ![]() , то достигнут максимальный
уровень иерархии p* = p
+ 1, для которого
, то достигнут максимальный
уровень иерархии p* = p
+ 1, для которого ![]() .
.
В противном случае
процедура стягивания подграфов повторяется для следующего уровня иерархии, причем
каждый раз, когда множество ![]() графа
графа
![]() содержит макровершины
содержит макровершины
![]() или
или ![]() , где q
≤ p, множество ребер распадается на два
подмножества
, где q
≤ p, множество ребер распадается на два
подмножества ![]() , такие,
что ребра из
, такие,
что ребра из ![]() указывают
пары конфликтных операций исходной программы [8, 9], а
указывают
пары конфликтных операций исходной программы [8, 9], а ![]() включает ребра
включает ребра ![]() и
и
![]() , описывающие для выделенных
макроопераций псевдоконфликты доступа к общим ресурсам процессора.
, описывающие для выделенных
макроопераций псевдоконфликты доступа к общим ресурсам процессора.
Псевдоконфликт
доступа к ресурсам определен для каждой пары информационно независимых элементов
из ![]() , включающей хотя бы одну
макровершину
, включающей хотя бы одну
макровершину ![]() или
или ![]() , где q ≤ р. Его суть заключается в невозможности параллельного
исполнения любой операции
, где q ≤ р. Его суть заключается в невозможности параллельного
исполнения любой операции ![]() с
операциями каждой макрокоманды, а также двух или более макроопераций одновременно.
Длины дуг, порождаемых в таких случаях, определяются как
с
операциями каждой макрокоманды, а также двух или более макроопераций одновременно.
Длины дуг, порождаемых в таких случаях, определяются как ![]() или для противоположного направления
или для противоположного направления ![]() , где
, где ![]() .
.
Окончательно иерархическая
модель Н** = (А*, V*, Е*) синтеза
параллельного объектного кода с циклами и ветвлениями имеет вид дизъюнктивного графа
![]() , построенного на основе преобразованной
билогической модели
, построенного на основе преобразованной
билогической модели ![]() , в которой
содержатся только вершины с конъюнктивной логикой, где
, в которой
содержатся только вершины с конъюнктивной логикой, где ![]() , а множество ребер
, а множество ребер ![]() определяет
пары конфликтных операций и макроопераций программы. Характерной особенностью модели
Н** является неопределенность временных характеристик
определяет
пары конфликтных операций и макроопераций программы. Характерной особенностью модели
Н** является неопределенность временных характеристик ![]() и
и
![]() макроопераций
макроопераций![]() и
и ![]() , где
, где ![]() , до завершения процедуры синтеза
КС каждой макрокоманды.
, до завершения процедуры синтеза
КС каждой макрокоманды.
Алгоритм синтеза КС объектной программы
Для решения задачи глобальной оптимизации параллельного кода при синтезе объектных программ с циклами и ветвлениями предлагается следующий итерационный алгоритм, который базируется на рассмотренной дизъюнктивной иерархической модели, а для определения временных характеристик макрокоманд использует процедуру синтеза последовательности командных слов для линейного фрагмента программы по заданному критерию качества [8].
Данные:
иерархическая модель синтеза Н** = (А*, V*,
Е*); множества ![]() вложенных
дизъюнктивных графов информационно-структурных зависимостей операций ЛУ программы,
где
вложенных
дизъюнктивных графов информационно-структурных зависимостей операций ЛУ программы,
где ![]() ;
максимальный уровень иерархии p*.
;
максимальный уровень иерархии p*.
Результаты: последовательность
LW = (LW1,
LW2, ..., LWN)
КС для программы в целом; списки ![]() КС для линейных участков, представленных дизъюнктивными
графами
КС для линейных участков, представленных дизъюнктивными
графами ![]() .
.
Шаг 1. Присвоить p = 0.
Шаг 2. Если p = p*, то выполнить переход к шагу 6.
Шаг 3. Для
каждой вершины ![]() графа
графа
![]() выполнить синтез последовательности
выполнить синтез последовательности
![]() и
и ![]() КС по заданному критерию качества. Определить время
КС по заданному критерию качества. Определить время ![]() исполнения макрооперации
исполнения макрооперации ![]() , где
, где ![]() — число тактов выполнения макрокоманды
— число тактов выполнения макрокоманды ![]() .
.
Шаг 4. Для
каждой вершины ![]() графа
графа
![]() выполнить по заданному
критерию качества синтез списков
выполнить по заданному
критерию качества синтез списков ![]() и
и ![]() КС для альтернативных ветвей.
Определить время
КС для альтернативных ветвей.
Определить время ![]() исполнения
и сформировать
исполнения
и сформировать ![]() список командных слов для составной макрокоманды
список командных слов для составной макрокоманды ![]() где
где ![]() — ветвь, исполняемая
при ложном, а
— ветвь, исполняемая
при ложном, а ![]() —
при истинном результате проверки условия ветвления.
—
при истинном результате проверки условия ветвления.
Шаг 5. Присвоить p = p + 1 и выполнить переход к шагу 2.
Шаг 6. На основе дизъюнктивного графа Н** выполнить синтез последовательности LW = (LW1, LW2,..., LWN) с циклами и ветвлениями.
Шаг 7. В
полученном списке LW найти макрокоманду ![]() с временем исполнения Tx = N(x),
где x =
с временем исполнения Tx = N(x),
где x = ![]() или
или
![]() и заменить фрагмент
и заменить фрагмент
![]() на последовательность
командных слов LW(x).
на последовательность
командных слов LW(x).
Шаг 8. Если список LW изменился, повторить выполнение шага 7. В противном случае конец алгоритма.
Следует отметить,
что представленный алгоритм позволяет выполнять синтез объектного кода как после,
так и во время формирования иерархической модели глобальной оптимизации. Во втором
случае синтез соответствующих списков ![]() или
или ![]() может быть проведен сразу же после стягивания фрагментов
билогического графа в вершины
может быть проведен сразу же после стягивания фрагментов
билогического графа в вершины ![]() или
или
![]() .
.
Покажем преимущества предлагаемого подхода на примере решения задачи синтеза параллельной объектной программы LW c циклами и ветвлениями по критерию минимального времени исполнения.
Пусть фрагмент
исходной программы, представленной в тетрадной форме, а также матрица ![]() конфликтов операций, где cij
= 1, если операции, ai и aj
не могут быть выполнены параллельно из-за необходимости использования общих ресурсов
процессора, и cij = 0 — в противном случае,
имеют следующий вид:
конфликтов операций, где cij
= 1, если операции, ai и aj
не могут быть выполнены параллельно из-за необходимости использования общих ресурсов
процессора, и cij = 0 — в противном случае,
имеют следующий вид:
a1 = (add, B, 10, D);
a2 = (add, C, 2, T1);
a3 = (sub, D, T1, T2);
a4 = (jmp, T2, , a7);
a5 = (add, T2, 1, Y);
a6 = (jm, , , a8);
a7 = (store, T2, , Y);
a8 = (sub, Y, Z, T3);
a9 = (add, T1, X, T4);
a10 = (add, T4, 3, T5);
a11 = (store, T5, , D).

Таблица
Синтез командных слов для линейных участков
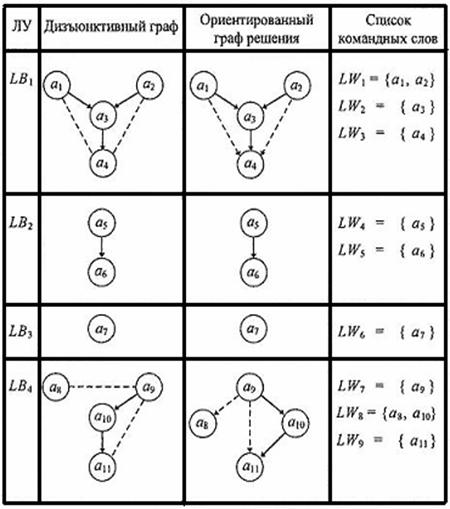
Фрагмент программы содержит четыре ЛУ:
LB1 = (a1, a2, a3, a4);
LB2 = (a5, a6);
LB3 = (a7);
LB4 = (a8, a9, a10, a11),
где LB2
и LB3 являются альтернативными, так как
при конкретной реализации программы выполняется только один из них. Время выполнения
любой операции составляет один такт, а операнды ![]() представляют собой промежуточные результаты, сформированные
компилятором.
представляют собой промежуточные результаты, сформированные
компилятором.
Формирование последовательностей длинных КС для каждого ЛУ в отдельности показаны в таблице. Время исполнения фрагмента программы в целом составляет восемь и семь тактов по трассам LB1, LB2, LB4 и LB1, LB3, LB4 соответственно.
Модель синтеза КС, учитывающая глобальную
структуру исходного фрагмента программы, формируется на основе билогического графа
(рис. 3, a), где символом & обозначена конъюнктивная
логика вершин. Иерархическая модель H** = (А*,
V*, Е*), приведенная на рис. 3, б, определяется
как дизъюнктивный граф ![]() , множество
вершин
, множество
вершин ![]() которого содержит
одну составную макровершину
которого содержит
одну составную макровершину ![]() ,
полученную стягиванием альтернативных ветвей LB2
и LB3,. Время реализации соответствующей
макрооперации
,
полученную стягиванием альтернативных ветвей LB2
и LB3,. Время реализации соответствующей
макрооперации ![]() определяется
по результатам синтеза КС для линейных участков LB2
и LB3, показанным в таблице.
определяется
по результатам синтеза КС для линейных участков LB2
и LB3, показанным в таблице.

Рис. 3. Модели глобальной оптимизации кода:
а — билогический граф программы; б — иерархический дизъюнктивный граф; в — ориентированный граф, определяющий решение; г — список командных слов объектной программы
Множество Е* определяется
как ![]() , где ребра
, где ребра ![]() , показанные штриховой линией, задают
конфликтные пары операций исходной программы (cij
= 1). Длина дуги (ai, aj)
или (aj, ai),
полученной из такого ребра, определяется видом конфликта по ресурсам [8—10]
и для данного примера во всех случаях l(ai,
aj) = l(aj, ai)
= 1.
, показанные штриховой линией, задают
конфликтные пары операций исходной программы (cij
= 1). Длина дуги (ai, aj)
или (aj, ai),
полученной из такого ребра, определяется видом конфликта по ресурсам [8—10]
и для данного примера во всех случаях l(ai,
aj) = l(aj, ai)
= 1.
Ребра ![]() , показанные пунктирной линией, описывают
псевдоконфликты макровершины отношением предшествования, что гарантирует сохранение
логики программы в процессе синтеза КС. Длины порождаемых дуг определяются как
, показанные пунктирной линией, описывают
псевдоконфликты макровершины отношением предшествования, что гарантирует сохранение
логики программы в процессе синтеза КС. Длины порождаемых дуг определяются как ![]() , где
, где ![]() - время реализации макрокоманды
- время реализации макрокоманды
![]() операции
операции ![]() соответственно. Для данного примера получаем:
соответственно. Для данного примера получаем:
![]() и
и ![]() .
.
Искомый орграф
Gi* = (A,
Vi*) с минимальной длиной критического
пути, порождаемый дизъюнктивным графом ![]() ,
приведен на рис. 3, в. Эквивалентная параллельная объектная программа LW содержит семь командных слов (рис. 3, г), причем
время выполнения составляет шесть и семь тактов по трассам LB1,
LB2, LB4
и LB1, LB3,
LB4 соответственно.
,
приведен на рис. 3, в. Эквивалентная параллельная объектная программа LW содержит семь командных слов (рис. 3, г), причем
время выполнения составляет шесть и семь тактов по трассам LB1,
LB2, LB4
и LB1, LB3,
LB4 соответственно.
* * *
В статье показана возможность и предложен метод решения задачи глобальной оптимизации параллельных объектных программ для RISC-процессоров с управлением по технологии VLIW, основанный на применении иерархической графовой модели, которая представляется множеством вложенных дизъюнктивных графов информационно-структурных зависимостей [9]. Это позволяет использовать единые алгоритмы [8] синтеза длинных КС объектной программы как для отдельных ЛУ, так и для программ с циклами и ветвлениями в целом, причем во втором случае достигается существенное сокращение общего числа КС и времени реализации за счет параллельного исполнения операций, принадлежащих разным линейным участкам исходной программы.
Список литературы
1. Трахтенгерц Э. А. Программное обеспечение параллельных процессов. М.: Наука, 1987. 272 с.
2. Французов Ю. А. Обзор методов распараллеливания кода и программной конвейеризации // Программирование. 1992. № 3. С. 16-37.
3. Local microcode compaction techniques / D. Landscov, S. Davidson, B. Shriver, P. W. Mallett // ACM Comput. Surveys. 1980. V. 12. № 3. P. 261-294.
4. Евстигнеев В. А. Некоторые особенности программного обеспечения ЭВМ с длинным командным словом // Программирование. 1991. № 2. С. 69—80.
5. Riscman E. M., Foster С. С. The inhibition of potential parallelism by conditional jumps // IEEE Trans. Comput. 1972. V. C-21. № 12. P. 1405-1411.
6. Fisher J. A. Trace scheduling: A technique for global microcode compaction // IEEE Trans. Comput. 1981. V. C-30. № 7. P. 478-490.
7. Nicolau A. Uniform parallelism exploitation in ordinary programs // Proc. of the 1985 Intern. Conf. on Parallel Processing, Aug. 1985. P. 614-618.
8. Скворцов С. В. Оптимизация кода для суперскалярных процессоров с использованием дизъюнктивных графов // Программирование. 1996. № 2. С. 41—52.
9. Корячко В. П., Скворцов С. В., Телков И. А. Модель планирования параллельных процессов в суперскалярных процессорах// Информационные технологии. 1997. № 1. С. 8—12.
10. Скворцов С. В. Целочисленные модели оптимизации кода по критерию времени // Информационные технологии. 1997. № 10. С. 2-7.
11. Грис Д. Конструирование компиляторов для цифровых вычислительных машин. М.: Мир, 1975. 544 с.
12. Головкин Б. А. Расчет характеристик и планирование параллельных вычислительных процессов. М.: Радио и связь, 1983. 272 с.
13. Рыжков А. П. Правильная билогическая граф-модель параллельного вычислительного процесса и ее свойства // Изв. АН СССР. Техническая кибернетика. 1976. № 2. С. 96—104.
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 9, 1998
ВЫЧИСЛИТЕЛЬНЫЕ СИСТЕМЫ И СЕТИ
Публикации с ключевыми словами: ООП, RISC, Параллельное программирование., VLIW, глобальная оптимизация, иерархия, модели программ, графовые модели, преобразование циклов, преобразование альтернатив
Публикации со словами: ООП, RISC, Параллельное программирование., VLIW, глобальная оптимизация, иерархия, модели программ, графовые модели, преобразование циклов, преобразование альтернатив
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



