научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#9 сентябрь 2005
В. П. Корячко, д-р техн. наук, проф.,
С. В. Скворцов, канд. техн. наук,
И. А. Телков, канд. техн. наук, Рязанская государственная радиотехническая академия
Математическая модель мобильных вычислений
Рассматриваются организация мобильных (переносимых) параллельных вычислений, ориентированных на системы с любой, в том числе нетрадиционной, архитектурой. Предлагается категорная иерархическая модель вычислительных алгоритмов, систем и программного обеспечения как результата отображения алгоритмов на аппаратные средства.
Идея создания программ, способных выполняться на любой вычислительной машине, зародилась достаточно давно. Об этом свидетельствует множество разработок и проектов, поддержанных в свое время на различных уровнях вплоть до международного [1—4]. Однако в последующие годы развитие индустрии программирования пошло по руслу интенсификации использования аппаратных средств и об идее "универсального" программирования временно забыли.
Изначально причиной интереса к переносимому, или мобильному, программному обеспечению были следующие факторы [1]:
· экономический, обусловленный соображениями сокращения затрат на перенос программ с одной платформы на другую;
· технологический, вызванный быстрой сменой аппаратной базы вычислительных систем;
· сетевой, определяемый возникновением и распространением корпоративных и глобальных вычислительных сетей.
В современной ситуации идея создания мобильного программного обеспечения (ПО) возродилась. Причиной тому послужили факторы как экономического, так и технологического характера. С экономической точки зрения к фактору экономии средств на разработке ПО [1] добавился фактор повторного использования программ {Reusable programs), который объясняется тем, что за прошедшие годы создан богатейший банк программных средств [5]. За истекший период развитие программной индустрии прошло ряд этапов [5], в результате чего значительно повысились требования к качеству, надежности и безопасности функционирования программ и программных комплексов, появилась концепция открытых информационных систем. Это в свою очередь вызвало интерес к надежному мобильному ПО. Кроме того, со стороны пользователей наметилась тенденция к снижению зависимости от поставщиков аппаратных и программных платформ.
В появившихся за последние годы работах по мобильным вычислениям рассматриваются в основном процессы переноса ПО между однопроцессорными платформами [6, 7]. Однако производительность однопроцессорных ЭВМ близка к пределу, обеспечиваемому технологической базой. Для продолжения наращивания вычислительной мощности в рамках современных технологий необходим переход к параллельным вычислениям. Ведущие фирмы-производители уже сосредоточили свои усилия на разработке многопроцессорных систем (например, [8—11]). Серьезным препятствием для перехода к "массовым" параллельным вычислениям является отсутствие единого рынка программ для подобной техники и принципиальные трудности в его расширении, вызванные качественным отличием в архитектуре многопроцессорных систем [12]. Для преодоления данного препятствия необходима разработка такой концепции переносимого (мобильного) программного обеспечения, на базе которой возможно создание единого рынка программных средств однопроцессорных и многопроцессорных вычислительных систем.
Термин мобильное программное обеспечение {portable software) будем использовать, в соответствии с [6], применительно к таким программам, которые могут быть откомпилированы и корректно выполнены (или корректно интерпретированы) без каких-либо изменений. Программы, для корректного выполнения которых необходимо внесение незначительных исправлений в исходный вариант, назовем переносимыми {transportable software).
При построении модели мобильного ПО необходимо учитывать возможность использования в инструментальной вычислительной системе разных принципов построения архитектуры. В основе переносимого ПО многопроцессорных вычислительных систем должна лежать такая формальная модель, которая удовлетворяла бы различным архитектурным принципам [13], определяемым двумя видами механизмов: механизмом управления и механизмом передачи данных. Существует три основных типа архитектурной организации [13, 14], основанные на различных механизмах управления вычислениями:
· архитектуры с управлением потоком команд;
· архитектуры с управлением потоком данных;
· архитектуры с управлением потоком запросов.
Архитектуры с управлением потоком команд реализуют принудительное (синхронное) управление в однопроцессорных и многопроцессорных вычислительных системах. В этом случае программист, инструментальная среда программирования или операционная система должны директивно определять последовательность выполнения вычислений. Архитектуры с управлением потоком данных реализуют принцип параллельного управления потоком данных (автоматическое выполнение вычислений по готовности аргументов), а архитектуры с управлением потоком запросов — рекурсивный принцип (автоматическое выполнение вычислений по запросу результата). В последних двух случаях параллельное выполнение программы осуществляется естественным путем по мере продвижения вычислительного процесса.
Значительное влияние на организацию вычислительного процесса оказывает также механизм доступа к данным. Доступ к данным может быть организован либо посредством ссылок к глобально доступным областям данных (доступ по имени), либо с помощью дублирования данных в аргументах исполняемых операторов (доступ по значению). В основе современных архитектур вычислительных систем лежат различные комбинации механизмов доступа к данным и управления [14, 15].
Универсальная модель вычислений должна удовлетворять следующим условиям:
· модель данных не должна зависеть ни от разрядности инструментальной машины, ни от формы представления в ней любого вида информации (например, форматов представления действительных чисел или порядка следования байтов в слове);
· модель алгоритма не должна быть ориентирована на какую-либо определенную архитектуру (т. е. не должна явно определять механизмы данных и управления) и не должна использовать временные и аппаратные характеристики инструментальной ЭВМ.
При построении универсальной модели вычислений необходимо опираться на такие фундаментальные понятия, как вычислительный алгоритм и вычислительная машина. В качестве основного объекта будем рассматривать вычислительный алгоритм (или вычислительную функцию [16]), под которым будем понимать прикладной алгоритм, ориентированный на выполнение на цифровой вычислительной системой с использованием арифметических действий (и численных методов на их основе) и логики предикатов первого порядка. Под универсальной вычислительной машиной (УВМ) будем понимать машину, способную выполнять любой вычислительный алгоритм, а под универсальной абстрактной вычислительной машиной — УВМ, не имеющую физической реализации и поэтому свободную от детализации ее устройств и механизмов исполнения алгоритма. Детализация универсальной абстрактной вычислительной машины может изменяться в зависимости от уровня абстракции. Для построения формальной модели мобильного ПО введем ряд определений.
Определение 1. Информационным пространством вычислительного алгоритма A будем называть многомерное множество Xn всех возможных (входных, выходных, промежуточных) данных Xi (i = 1,..., n), которые используются в алгоритме.
Определение 2. Информационным геометрическим объектом ранга 0
информационного пространства алгоритма A будем
называть конкретное значение элемента пространства ![]() .
.
Информационным геометрическим объектом ранга 1 информационного пространства вычислительного алгоритма A будем называть вектор значений информационного геометрического объекта ранга 0
![]() .
.
Определение 3. Функциональным геометрическим объектом будем
называть функцию ![]() , областью определения и
областью значений которой являются подпространства Хk и X
информационного пространства
, областью определения и
областью значений которой являются подпространства Хk и X
информационного пространства ![]() .
.
В информационном пространстве можно выделить подпространства информационных объектов по следующим критериям:
·
по возможности модификации — подпространства переменных ![]() и
постоянных
и
постоянных ![]() информационных объектов;
информационных объектов;
·
по расположению относительно области вычислений алгоритма —
подпространства входных ![]() , промежуточных
, промежуточных ![]() и выходных
и выходных ![]() информационных объектов;
информационных объектов;
·
по характеру информации — подпространства данных ![]() и
управления (управляющей информации)
и
управления (управляющей информации) ![]() ;
;
· по типу информации — подпространства действительных, целых (дискретных), логических и символьных информационных объектов.
Подпространства входных I и выходных O объектов обеспечивают взаимодействие алгоритма с внешней информационной средой, а подпространство промежуточных объектов W определяет внутреннюю область вычислений алгоритма. При этом между подпространствами соблюдаются следующие соотношения:
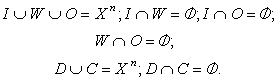
По типам подпространств областей определения и значений можно выделить следующие классы функциональных объектов:
·
обработки данных ![]() ;
;
·
вычисления управляющих предикатов ![]() ;
;
·
вычисления данных по управляющим предикатам ![]() ;
;
·
логические ![]() ;
;
·
приема информации из внешней информационной среды: прием данных ![]() и прием управляющей
информации
и прием управляющей
информации ![]() ;
;
·
передачи информации во внешнюю информационную среду: передача
данных ![]() и
передача управляющей информации
и
передача управляющей информации ![]() ;
;
·
определения констант: константы данных ![]() и константы управляющей информации
и константы управляющей информации ![]() ;
;
Определение 4. Универсальной формой вычислительного алгоритма над информационным пространством Xn будем называть категорию
A = (Ob A Mor A), (1)
класс объектов которой Ob A составляют множества
Ob A = (X, F, L, V), (1а)
а класс морфизмов Mor A составляют отображения
A = (Ф, Ф’, Ф’’, Ф’’’). (1б)
Здесь X — множество
информационных геометрических объектов информационного пространства; F = (f1,…,
fm) — множество функциональных
геометрических объектов информационного пространства; L = (l1,…,
lp) — множество числовых или
символьных идентификаторов информационных геометрических объектов (номера в
таблице переменных или имена переменных алгоритма); V = (v1,
v2,…, vk)
— множество (кортеж) функциональных геометрических объектов (vi![]() F), определяющее совместно с отображениями
Ф" и Ф'" информационные связи функциональных объектов
(или порядок выполнения в случае последовательного выполнения алгоритма);
F), определяющее совместно с отображениями
Ф" и Ф'" информационные связи функциональных объектов
(или порядок выполнения в случае последовательного выполнения алгоритма);
Ф: L![]() X — отображение идентификаторов
в информационном пространстве; Ф': V
X — отображение идентификаторов
в информационном пространстве; Ф': V![]() F — отображение объектов V в множество объектов F; Ф": L
F — отображение объектов V в множество объектов F; Ф": L![]() V и Ф'": V
V и Ф'": V![]() L — отображения, определяющие
информационные связи функциональных объектов (соответственно входные и
выходные).
L — отображения, определяющие
информационные связи функциональных объектов (соответственно входные и
выходные).
Определение алгоритма в виде категории (1) охватывает как алгоритмы с локальными преобразованиями колмогоровского типа (машины Колмогорова, Поста, Тьюринга [16]), так и модели с нелокальными шагами (например, такие как нормальные алгорифмы Маркова [17] или равнодоступная адресная машина [18]). Локальность действий в смысле Колмогорова связана с разбиением алгоритма на шаги ограниченной сложности, каждый из которых работает в пределах "активной части" состояния системы. Подобные локальные преобразования можно представить как действия в подпространствах, которые описываются отображениями Ф" и Ф'". Нелокальные преобразования возникают в том случае, если рассматривать преобразования Ф" и Ф"' как отображения из одного пространства в другое.
Понятие функционального объекта информационного пространства аналогично понятиям непосредственной переработки Колмогорова, локальной операции [16], функционала Клини [16] или вычислимого оператора Роджерса [19], определенного в рамках геометрической (пространственной) модели.
Определение 5. Универсальной абстрактной вычислительной машиной будем называть систему-исполнитель универсального абстрактного вычислительного алгоритма, представленную в виде категории [20]
S = (Ob S Mor S), (2)
класс объектов которого Ob S составляют множества
Ob S = (U, M, F, O C), (2а)
а класс морфизмов Mor S — отображения
Mor S = (![]() )
(2б)
)
(2б)
Здесь U —
универсальный вычислитель (процессор); M — память универсальной абстрактной вычислительной машины
(единое поле памяти); F —
система команд (арифметико-логические операции, операции для работы с памятью и
операции ввода-вывода); O
— размещение информации в памяти (адресация); C — программа (код) управления; α:
O![]() M — отображение, определяющее размещение
информации в памяти; β: C
M — отображение, определяющее размещение
информации в памяти; β: C![]() F — отображение операторов
программы в систему команд; y: C
F — отображение операторов
программы в систему команд; y: C![]() U — отображение операторов на исполняющее
устройство (процессор); ф: L
U — отображение операторов на исполняющее
устройство (процессор); ф: L![]() V и
V и ![]() : C
: C![]() O — отображение, определяющее взаимосвязи
операторов по данным (соответственно входные и выходные операнды).
O — отображение, определяющее взаимосвязи
операторов по данным (соответственно входные и выходные операнды).
Универсальная абстрактная вычислительная машина представляет собой таксон верхнего уровня, расположенный над систематическими категориями классификаций МПВС, предлагаемых в [13, 21]. Итоговый вариант классификации приведен на рисунке. Таксон уровня II занимают типы абстрактных архитектур потоков команд, данных и запросов. Первый из них можно выделить в надтип архитектур с принудительным управлением, а два других — объединить в надтип архитектур с естественным управлением. На следующем III уровне располагается таксон классов абстрактных машин (АВМ). Архитектура потока команд представлена на нем машинами классификации Флинна [21]: ОКОД, ОКМД, МКОД, МКМД. Архитектура потока данных представлена абстрактными машинами потока данных с общей локальной памятью, а архитектура потока запросов — абстрактными машинами потока запросов, среди которых можно выделить АВМ с редукцией строк и АВМ с редукцией графов [13]. На последнем IV уровне находятся конкретные аппаратные реализации вычислительных систем.

Классификация вычислительных систем
Определение 6. Программной реализацией алгоритма A на исполнителе S, или просто программой Ps, назовем функтор [20] вида
PS: A![]() S,
S,
где A — универсальная форма вычислительного алгоритма, определяемая как категория (1) с классами (1а) и (16); S — универсальная абстрактная вычислительная машина, определяемая как категория (2) с классами (2а) и (2б); PS — программа универсальной абстрактной вычислительной машины S.
Процесс детализации инструментальной базы исполнителя алгоритмов можно записать в виде последовательности функторов (отображений) уточняемых систем
S![]() S
S![]() S
S![]() S(3)
S(3)
где S — модель универсальной абстрактной вычислительной машины; S — модель уровня абстрактной архитектуры; S — модель уровня абстрактной машины; S — конкретная реализация многопроцессорных вычислительных систем.
Связанные с преобразованием функторов (3) преобразования алгоритмической и программной части вычислений можно представить в виде диаграммы

где A — категория универсальной формы вычислительного алгоритма; A, А, А — категории вычислительных алгоритмов уровней абстрактной архитектуры, абстрактной машины и конкретной реализации; (P — функтор-программа универсальной абстрактной вычислительной машины; P, P, P — функторы, определяющие программы уровней абстрактной архитектуры, абстрактной машины и конкретной ВС.
Определение 7. Функтором конкретизации будем называть функтор, определяющий отображение элементов модели вычислений какого-либо таксона в элементы модели нижестоящего таксона.
Функторы r, c, t и r, c, t описывают соответственно преобразования конкретизации структуры многопроцессорных вычислительных систем и реализуемого на ней алгоритма:
·
конкретизации архитектуры r. S ![]() S и r: A
S и r: A ![]() R;
R;
·
конфигурирования архитектуры c: S![]() S и t: A
S и t: A![]() A;
A;
·
параметризации АВМ t: S![]() S и t:
A
S и t:
A![]() A.
A.
При конкретизации архитектуры определяются основополагающие характеристики — механизмы данных и управления. В процессе конфигурирования архитектуры определяют структуру абстрактной машины: число модулей памяти, обработки, управления, коммутации, ввода-вывода и их взаимосвязи. В ходе параметризации абстрактной машины определяют количественные характеристики конкретной многопроцессорной вычислительной системы — разрядность модулей и шин, временные показатели, форматы данных и команд.
Класс объектов категорий A,
A, A, А представляет собой
множество (точнее — конечное множество конечных множеств), поэтому функторы,
используемые в диаграмме (4) представляют собой с точки зрения теории категорий
[20] элементы категорий функторов (диаграмм). Например, функтор, определяющий
программу универсальной абстрактной вьиислительной машины P: A![]() S, является элементом категории P (A, S). Объектами этой категории являются
всевозможные функторы P: A
S, является элементом категории P (A, S). Объектами этой категории являются
всевозможные функторы P: A![]() S, определяющие множество отображений
категории A на категорию S. Следовательно, практическая
реализация функтора P: A
S, определяющие множество отображений
категории A на категорию S. Следовательно, практическая
реализация функтора P: A![]() S требует выбора одного из множества
функторов, входящих в категорию P
(A, S). Таким образом, диаграмма (4)
представляет собой набор задач оптимизации, заключающихся в анализе
соответствующих категорий функторов и выборе из множества единственного
(оптимального) функтора-программы или функтора конкретизации.
S требует выбора одного из множества
функторов, входящих в категорию P
(A, S). Таким образом, диаграмма (4)
представляет собой набор задач оптимизации, заключающихся в анализе
соответствующих категорий функторов и выборе из множества единственного
(оптимального) функтора-программы или функтора конкретизации.
Исходя из вышесказанного, можно утверждать, что наиболее общее описание
программных средств (определяемое уровнем ПО универсальной абстрактной
вычислительной машины или функтором P:
A![]() S) должно соответствовать модели
универсальной формы вычислительного алгоритма и не должно содержать элементов:
S) должно соответствовать модели
универсальной формы вычислительного алгоритма и не должно содержать элементов:
1) конкретизации архитектуры, т. е. описание программы должно допускать любую форму механизмов управления и данных [9—11];
2) конфигурирования абстрактной архитектуры, т. е. описание программы не должно содержать прямые указания на количественные характеристики структурной организации уровня АВМ;
3) параметризации абстрактной машины, т. е. описание программы не должно содержать ссылки на конкретные форматы машинных команд и данных, а также использовать разрядности операндов (их внутреннюю организацию) и учитывать длительность операций.
Современные языки программирования не удовлетворяют данному комплексу требований. Если нижний уровень абстрагирования (3) можно считать освоенным (например, в виртуальной Java-машине [22]), то требования (1) и (2) в современных языках программирования не соблюдаются. Так, языки параллельного программирования (начиная с различных версий параллельного ФОРТРАНА и кончая такими языками, как Модула, Ада, Оккам) используют конструкции принудительного распараллеливания и количественные характеристики вычислительной системы (например, число параллельно работающих модулей). Кроме того, языки программирования разрабатывались с ориентацией на конкретную архитектуру и не приспособлены для поддержки различных механизмов управления и данных. Например, в подавляющем большинстве языков программирования не поддерживается принцип однократного присваивания, обязательный для архитектур потоков данных [15].
Таким образом, для построения мобильного ПО необходимо осуществить в практике программирования переход от использования языков программирования, ориентированных на аппаратные средства, к использованию алгоритмических языков, предназначенных для описания "чистых" алгоритмов без привязки к конкретным техническим средствам. Подобный подход, однако, не исключает существования прежних языков программирования, как и всего машинно-зависимого ПО. Они должны составлять базу (ядро) виртуальной машины, настроенной на исполнение мобильного ПО, подобно тому, как реализуется машинно-зависимое ядро JavaOS виртуальной Java-машине. Поэтому предложенная модель мобильного ПО ориентирована не только на описание мобильных программ и определение требований к языку их написания, но и может быть использована для построения модели виртуальной параллельной машины, предназначенной для выполнения мобильного ПО на любых МВС.
Для решения задач конкретизации, конфигурирования и параметризации иерархической модели (4) необходим достаточно мощный по своим возможностям математический аппарат, в качестве которого целесообразно использовать тензорную алгебру [23]. Основными достоинствами тензорного аппарата применительно к вычислительным системам являются [24]:
· возможность описания разнородных составляющих вычислительного процесса (алгоритмов, программ, аппаратуры);
· отсутствие ограничений на сложность моделируемых объектов;
· возможность выполнения алгебраических преобразований (например, с целью оптимизации системы).
Список литературы
1. Мобильность программного обеспечения / Под ред. П. Брауна. М.: Мир, 1980. 336 с.
2. Brown W. S. Software Portability, Software Engeneering Techniques // Report on a Conference Sponsored by the NATO Science Committee. Brussels. 1969. P. 80—84.
3. Richards M. The Portability of the BCPL Compiler // Software — Practice and Experience. 1971. N 1. P. 135—146.
4. Sable J. D. Transferability of data and program between computer systems // Proc. Spring Joint Computer Conference. 1969. P. 611-612.
5. Липаев В. В., Филипов Е. Н. Мобильность программ и данных в открытых информационных системах. М.: Научная книга, 1997. 368 с.
6. Hague S. J., Ford В. Portability: Prediction and Correction // Software-Practice and Experience. 1976. Vol. 6. N 1. P. 61—69.
7. Franz M. Code-Generation On-the-Fly: A Key for Portable Software. PhD thesis (ETH N 10497). Zurich, ETH. 97 p.
8. Коваленко Е. Система Sequent NUMA-Q // Открытые системы. 1997. № 2. С. 6—13.
9. Кузьминский М. Архитектура S2MP — свежий взгляд на cc-NUMA// Открытые системы. 1997. № 2. С. 14—21.
10. Солтис Ф. Основы AS/400. М.: Русская редакция, 1997. 376 с.
11.Новосельцев С. Let it Be! // КомпьютерПресс. 1996. № 2. С. 151—158.
12. Телков И. А. Математические аспекты универсального языка параллельного программирования // Информационные технологии. Системы обработки и передачи информации: Межвуз. сб.; Рязань, РГРТА, 1996. С. 67—73.
13. Головкин Б. А. Вычислительные системы с большим числом процессоров. М.: Радио и связь, 1995. 320 с.
14. Treleaven Р. С, Brownbridge D. R., Hopkins R. P. Data-Driven and Demand-Driven Computer Architecture // Computing Surveys. 1982. Vol. 14. N. 1. P. 93—143.
15. Системы параллельной обработки. Под ред. Д. Ивенса. М.: Мир, 1985. 416 с.
16. Успенский В. А., Семенов А. Л. Теория алгоритмов: основные открытия и приложения. М.: Наука, 1987. 288 с.
17. Марков А. А., Нагорный Н. М. Теория алгорифмов. М.: Наука, 1984. 432 с.
18. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. М.: Мир, 1979. 536 с.
19. Роджерс X. Теория рекурсивных функций и эффективная вычислимость. М.: Мир, 1972. 624 с.
20. Фултон У., Мак-Ферсон Р. Категорный подход к изучению пространств с особенностями. М.: Мир, 1983. 216 с.
21. Flynn M. J. Some computer organizations and their effectiveness // IEEE Transaction on Computers. 1972. Vol. C-21. N 9. P. 948-960.
22. Hopson K. S., Ingram S. E. Developing Professional Java Applets. Sams, net Publishing, 1996.
23. Кулагин В. П. Проблемы анализа и синтеза структур параллельных вычислительных систем // Информационные технологии. 1997. № 1. С. 2—8.
24. Телков И. А. Тензорная модель программных средств параллельных вычислительных систем // Вестник РГРТА. 1996. № 1. С. 32—39.
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 11, 1998
ВЫЧИСЛИТЕЛЬНЫЕ СИСТЕМЫ И СЕТИ
Ключевые слова: Параллельное программирование, переносимость программ, классификация вычислительных систем, требования к программным средствам.
Публикации с ключевыми словами: Параллельное программирование., переносимость программ, классификация вычислительных систем, требования к программным средствам
Публикации со словами: Параллельное программирование., переносимость программ, классификация вычислительных систем, требования к программным средствам
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



