научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 03, март 2013
DOI: 10.7463/0313.0543198
УДК 534.1
Россия, МГТУ им. Н.Э. Баумана
При исследовании вынужденных стационарных случайных колебаний линейных систем с конечным числом степеней свободы ![]() [1, 2, 3, 4] широко используются функции частоты, связывающие перемещение в некоторой точке системы с воздействием в какой-либо другой точке при установившихся гармонических колебаниях. Эти функции называют передаточными функциями, динамическими податливостями, гармоническими коэффициентами влияния или элементами матрицы Грина в пространстве Фурье [2, 3].
[1, 2, 3, 4] широко используются функции частоты, связывающие перемещение в некоторой точке системы с воздействием в какой-либо другой точке при установившихся гармонических колебаниях. Эти функции называют передаточными функциями, динамическими податливостями, гармоническими коэффициентами влияния или элементами матрицы Грина в пространстве Фурье [2, 3].
Передаточная функция ![]() зависит от угловой частоты внешнего воздействия
зависит от угловой частоты внешнего воздействия ![]() и определяет перемещение
и определяет перемещение ![]() -той степени свободы на гармоническое воздействие, приложенное по
-той степени свободы на гармоническое воздействие, приложенное по ![]() -той степени свободы. Номера степеней свободы
-той степени свободы. Номера степеней свободы ![]() ,
,![]() принимают значения
принимают значения ![]() . Коэффициенты
. Коэффициенты ![]() при различных значениях номеров степеней свободы могут быть собраны в некоторую матрицу
при различных значениях номеров степеней свободы могут быть собраны в некоторую матрицу ![]() размером
размером ![]() , которую называется матрицей передаточных функций, матрицей гармонических коэффициентов влияния или матрицей динамических податливостей.
, которую называется матрицей передаточных функций, матрицей гармонических коэффициентов влияния или матрицей динамических податливостей.
Наиболее распространенным способом вычисления коэффициентов матрицы ![]() является способ, основанный на использовании собственных частот и форм колебаний [1]. Число учитываемых тонов колебаний
является способ, основанный на использовании собственных частот и форм колебаний [1]. Число учитываемых тонов колебаний ![]() является при этом ограниченным, для больших конечно-элементных моделей обычно
является при этом ограниченным, для больших конечно-элементных моделей обычно ![]() . Естественно, возникает вопрос о погрешности усечения ряда. В настоящей статье применительно к вычислению матрицы динамических податливостей, найденной с учетом классического внутреннего демпфирования, определяется поправка, позволяющая существенно снизить погрешность усечения.
. Естественно, возникает вопрос о погрешности усечения ряда. В настоящей статье применительно к вычислению матрицы динамических податливостей, найденной с учетом классического внутреннего демпфирования, определяется поправка, позволяющая существенно снизить погрешность усечения.
1.Получение передаточной матрицы для системы с демпфированием
Для вычисления матрицы передаточных функций рассмотрим задачу о стационарных колебаниях системы с ![]() степенями свободы с учетом демпфирования [1,3,5]. Динамическое уравнение движения в матричной форме имеет вид:
степенями свободы с учетом демпфирования [1,3,5]. Динамическое уравнение движения в матричной форме имеет вид:
![]() (1)
(1)
Здесь ![]() - матрица массы,
- матрица массы, ![]() - матрица демпфирования,
- матрица демпфирования, ![]() - матрица жесткости.
- матрица жесткости. ![]() ,
, ![]() и
и ![]() , соответственно, векторы ускорений, скоростей и перемещений узловых точек,
, соответственно, векторы ускорений, скоростей и перемещений узловых точек, ![]() - амплитуда вынуждающей силы,
- амплитуда вынуждающей силы, ![]() угловая частота внешнего воздействия,
угловая частота внешнего воздействия, ![]() - начальная фаза,
- начальная фаза, ![]() - мнимая единица.
- мнимая единица.
Демпфирование предполагается классическим, то есть пропорциональным матрице жесткости (внутреннее демпфирование [3]):
![]() (2)
(2)
или матрице массы (внешнее демпфирование):
![]() , (3)
, (3)
где ![]() и
и ![]() - некоторые коэффициенты.
- некоторые коэффициенты.
Установившиеся колебания происходят по гармоническому закону с частотой вынуждающей силы. Поэтому решение уравнения (1) будем искать в виде:
![]() , (4)
, (4)
где ![]() - n-мерный вектор комплексных значений амплитуд колебаний узловых точек.
- n-мерный вектор комплексных значений амплитуд колебаний узловых точек.
Подставляя (4) в (1) получим:
![]() (5)
(5)
В случае классического демпфирования динамические уравнения движения могут быть преобразованы с использованием форм колебаний системы без демпфирования, то есть можно представить вектор амплитудных значений перемещений ![]() в виде разложения в ряд по собственным формам колебаний:
в виде разложения в ряд по собственным формам колебаний:
![]() (6)
(6)
Здесь q- комплексный n-мерный вектор координат форм, ![]() действительная матрица форм колебаний, в которой собственные векторы
действительная матрица форм колебаний, в которой собственные векторы ![]() , являющиеся решением симметричной обобщенной проблемы собственных значений (7):
, являющиеся решением симметричной обобщенной проблемы собственных значений (7):
![]() ,
, ![]() (7)
(7)
расположены по столбцам в порядке возрастания соответствующей им угловой частоты собственных колебаний ![]() (
(![]() - номер тона колебаний):
- номер тона колебаний):
![]() (8)
(8)
Предполагается, как обычно, что формы колебаний удовлетворяют соотношениям ![]() - и
- и ![]() - ортогональности:
- ортогональности:
![]()
![]() (9)
(9)
![]() - диагональная матрица собственных чисел
- диагональная матрица собственных чисел ![]() :
:
![]() (10)
(10)
![]() - единичная матрица.
- единичная матрица.
Для получения уравнения вынужденных стационарных колебаний в координатах форм, подставим (6) в (5), полученное выражение умножим слева на ![]() и используем соотношения ортогональности (9). В итоге приходим к уравнению:
и используем соотношения ортогональности (9). В итоге приходим к уравнению:
![]() (11)
(11)
Матрица ![]() - диагональная. Для случая, когда матрица демпфирования пропорциональна матрице жесткости:
- диагональная. Для случая, когда матрица демпфирования пропорциональна матрице жесткости:
![]() (12)
(12)
В случае пропорциональности матрице массы:
![]() (13)
(13)
![]() - вектор амплитудных значений обобщенных сил, определяется формулой:
- вектор амплитудных значений обобщенных сил, определяется формулой:
![]() (14)
(14)
Из уравнения (11) можно найти вектор ![]() комплексных значений координат форм:
комплексных значений координат форм:
![]() (15)
(15)
Матричное выражение, стоящее в круглых скобках, является диагональной матрицей. Легко найти матрицу обратную диагональной:
![]()
![]()

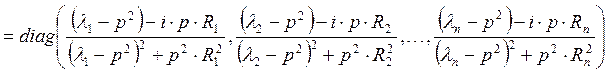 (16)
(16)
Коэффициенты демпфирования ![]() ,
, ![]() определяются по формулам (12) или (13), в зависимости от используемой модели демпфирования.
определяются по формулам (12) или (13), в зависимости от используемой модели демпфирования.
Связь между вектором амплитудных значений перемещений ![]() и вектором амплитудных значений сил
и вектором амплитудных значений сил ![]() может быть найдена путем подстановки в (15) формулы (6), связывающей перемещения и координаты форм, и (14), определяющей обобщенные силы:
может быть найдена путем подстановки в (15) формулы (6), связывающей перемещения и координаты форм, и (14), определяющей обобщенные силы:
![]() (17)
(17)
Матрица, связывающая между собой вектор амплитудных значений перемещений ![]() с вектором амплитудных значений сил
с вектором амплитудных значений сил ![]() , и является искомой матрицей передаточных функций
, и является искомой матрицей передаточных функций ![]() . Из (17) следует:
. Из (17) следует:
![]() (18)
(18)
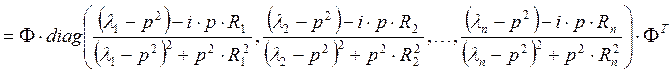
Как видно, матрица передаточных функций является комплексной, ее можно представить в виде суммы действительной ![]() и мнимой
и мнимой ![]() частей:
частей:
![]() (19)
(19)
Действительная часть:
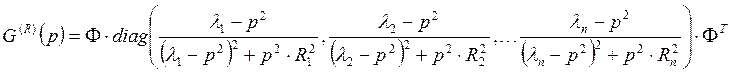 (20)
(20)
мнимая часть:
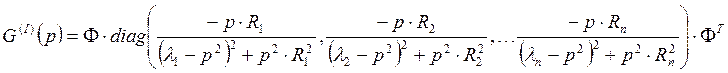 (21)
(21)
Отдельные коэффициенты матриц определяются суммой ряда по номеру тона колебаний. Коэффициенты ![]() действительной части матрицы динамических податливостей:
действительной части матрицы динамических податливостей:
 (22)
(22)
Коэффициенты ![]() мнимой части матрицы динамических податливостей:
мнимой части матрицы динамических податливостей:
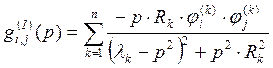 (23)
(23)
![]() - номер тона колебаний,
- номер тона колебаний, ![]() и
и ![]() - номера степеней свободы.
- номера степеней свободы.
2.Учет вклада отброшенных тонов колебаний в случае внутреннего демпфирования
При практических расчетах колебаний систем с большим числом степеней свободы, как правило, для учета демпфирования используется модель классического внутреннего демпфирования. Тогда коэффициенты демпфирования определяются формулой (12), а коэффициенты матрицы динамических податливостей
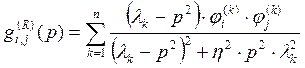 (24)
(24)
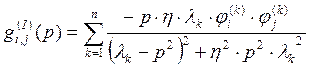 (25)
(25)
При вычислении коэффициентов матрицы динамических податливостей с помощью формул (24) и (25), так как конечно-элементная модель имеет большую размерность, используются не все ![]() частот и форм колебаний, а только ограниченная часть спектра -
частот и форм колебаний, а только ограниченная часть спектра - ![]() тонов колебаний. Вклад отброшенных тонов можно учесть приближенно, причем с хорошей точностью, используя подход, предложенный в работе [6] применительно к построению сокращенной модальной модели в системе без демпфирования. Так как для отброшенных тонов
тонов колебаний. Вклад отброшенных тонов можно учесть приближенно, причем с хорошей точностью, используя подход, предложенный в работе [6] применительно к построению сокращенной модальной модели в системе без демпфирования. Так как для отброшенных тонов ![]() , то при вычислении остатка ряда при
, то при вычислении остатка ряда при ![]() в формулах (24) и (25) можно пренебречь
в формулах (24) и (25) можно пренебречь ![]() по сравнению с
по сравнению с ![]() положить
положить ![]() . Разделяя ряды в (24) и (25) на две части запишем:
. Разделяя ряды в (24) и (25) на две части запишем:
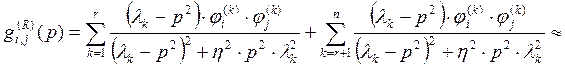
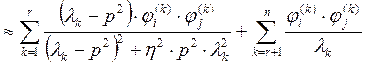 (26)
(26)
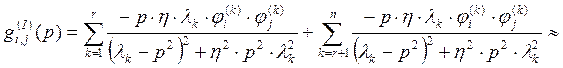
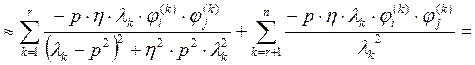
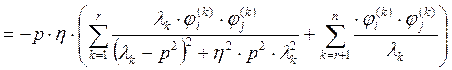 (27)
(27)
Остаток ряда, соответствующий отброшенным тонам колебаний содержит сумму
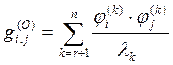 (28)
(28)
Такая же сумма встречается в [6], где она названа остаточной податливостью. Для нахождения ![]() используем следующий прием. Если положить в формуле (26)
используем следующий прием. Если положить в формуле (26) ![]() , мы получим значение податливости
, мы получим значение податливости ![]() для статической задачи:
для статической задачи:
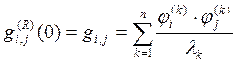 (29)
(29)
Коэффициенты этой матрицы могут быть найдены путем решения соответствующей задачи статики: ![]() равно перемещению по
равно перемещению по ![]() той степени свободы при приложении единичной силы по
той степени свободы при приложении единичной силы по ![]() той степени свободы.
той степени свободы.
Сравнивая (28) и (29) запишем
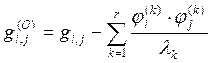 (30)
(30)
Согласно формуле (30) поправка получается путем вычитания из ![]() статического вклада
статического вклада ![]() тонов колебаний, учтенных в расчете. Таким образом, получаются следующие формулы для вычисления действительной и мнимой частей коэффициентов матрицы передаточных функций:
тонов колебаний, учтенных в расчете. Таким образом, получаются следующие формулы для вычисления действительной и мнимой частей коэффициентов матрицы передаточных функций:
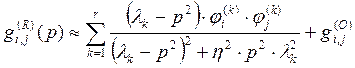 (31)
(31)
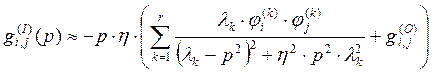 (32)
(32)
В полученных формулах учитывается вклад отброшенных тонов колебаний. В отличие от [6], рассмотрение проведено с учетом демпфирования. Передаточная матрица является комплексной, и поправки вносятся как в действительную, так и в мнимую часть.
3.Пример вычисления коэффициентов передаточной матрицы
Проиллюстрируем формулы, полученные в настоящей статье, на примере консольной балки. Передаточные функции для балки можно найти не только по формулам (31) и (32), но и, при отсутствии демпфирования, аналитически. Пусть балка заделана на левом конце, а на правом свободна. Найдем матрицу, связывающую перемещение и угол поворота на свободном конце балки с соответствующими силовыми факторами. Эта матрица имеет порядок ![]() и в силу симметрии имеет три независимых коэффициента, которые мы обозначим
и в силу симметрии имеет три независимых коэффициента, которые мы обозначим ![]() ,
, ![]() и
и ![]() . Эти коэффициенты связывают между собой амплитудные значения силовых факторов и компонент перемещений при гармоническом воздействии:
. Эти коэффициенты связывают между собой амплитудные значения силовых факторов и компонент перемещений при гармоническом воздействии: ![]() - поперечное перемещение с поперечной силой,
- поперечное перемещение с поперечной силой, ![]() - поперечное смещение с моментом,
- поперечное смещение с моментом, ![]() - угол поворота с моментом. При аналитическом решении задач о собственных колебаниях балок [3,5,7] используется безразмерный параметр
- угол поворота с моментом. При аналитическом решении задач о собственных колебаниях балок [3,5,7] используется безразмерный параметр ![]() , связанный с угловой частотой колебаний
, связанный с угловой частотой колебаний ![]() формулой:
формулой:
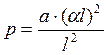 (33)
(33)
![]() -длина балки,
-длина балки, 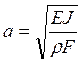 ,
, ![]() - модуль упругости,
- модуль упругости, ![]() - плотность,
- плотность, ![]() - площадь поперечного сечения,
- площадь поперечного сечения, ![]() - момент инерции.
- момент инерции.
Точные значения коэффициентов передаточной матрицы могут быть найдены путем аналитического решения задачи о вынужденных стационарных колебаниях консольной балки нагруженной на свободном конце силовыми факторами, изменяющимися по гармоническому закону. Последовательно решая задачи о нагружении единичной поперечной силой и единичным моментом, получим следующие аналитические выражения для передаточных функций как функций параметра ![]() , заменяющего частоту
, заменяющего частоту ![]() :
:
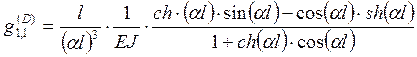 (34)
(34)
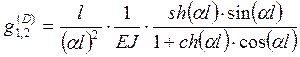 (35)
(35)
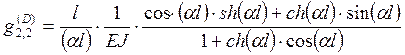 (36)
(36)
Для определения коэффициентов динамической податливости методом суммирования вкладов тонов колебаний форм необходимо вычислить частоты формы собственных колебаний. Значения ![]() , соответствующие собственным частотам консольной балки являются корнями характеристического уравнения [7]:
, соответствующие собственным частотам консольной балки являются корнями характеристического уравнения [7]:
![]() (37)
(37)
Таблица первых шести корней уравнения (37) приведена в [7], для высших тонов корни находились численно. Собственные числа после этого определялись по формуле:
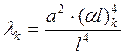 (38)
(38)
![]() номер тона колебаний. Для вычисления передаточных функций используются формы колебаний
номер тона колебаний. Для вычисления передаточных функций используются формы колебаний ![]() , нормированные по массе. Применительно к балке условие нормирования :имеет вид:
, нормированные по массе. Применительно к балке условие нормирования :имеет вид:
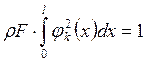 (39)
(39)
Значение перемещения на свободном конце балки:
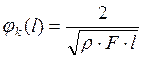 (40)
(40)
Угол поворота:
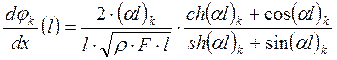 (41)
(41)
Значения статических податливостей, необходимые для вычисления поправок, равны
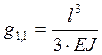 ;
; 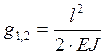 ;
; 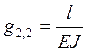 (42)
(42)
Сравнение численного и аналитического решений, а так же оценка влияния статической поправки проводилось в следующей последовательности. Вначале передаточные функции ![]() ,
, ![]() ,
, ![]() вычислялись без учета демпфирования и значения, полученные суммированием вкладов тонов колебаний, сравнивались результатами расчета по формулам (34), (35), (36). Затем проводились расчеты с учетом демпфирования при разном числе учитываемых тонов колебаний, так же с учетом и без учета найденной поправки. Вычисления поводились при единичных значениях
вычислялись без учета демпфирования и значения, полученные суммированием вкладов тонов колебаний, сравнивались результатами расчета по формулам (34), (35), (36). Затем проводились расчеты с учетом демпфирования при разном числе учитываемых тонов колебаний, так же с учетом и без учета найденной поправки. Вычисления поводились при единичных значениях ![]() ,
, ![]() и
и ![]() , так как эти параметры не оказывают влияния на скорость сходимости рядов и точность решения.
, так как эти параметры не оказывают влияния на скорость сходимости рядов и точность решения.
4.Сравнение точных и приближенных значений коэффициентов в системе без демпфирования
Наименьшие погрешности приближенных формул наблюдаются при частотах резонансов, наибольшие при частотах антирезонансов. Частоты резонансов, очевидно, для всех передаточных функций одинаковы, частоты антирезонансов (перехода значения коэффициента через нуль) у каждой функции свои. Значения безразмерного параметра ![]() , соответствующие частотам резонансов и антирезонансов приведены в таблице 1:
, соответствующие частотам резонансов и антирезонансов приведены в таблице 1:
Таблица 1. Частоты резонансов и антирезонансов.
Номер тона |
|
|
|
|
1 | 1.875104068712 | 3.926602312051 | 3.14159265359 | 2.365020372434 |
2 | 4.694091132974 | 7.068582745625 | 6.283185307177 | 5.497803919001 |
3 | 7.854757438238 | 10.210176122819 | 9.424777960776 | 8.639379828695 |
В таблицах 2-4 указаны погрешности расчета действительной части коэффициентов динамической податливости. В таблице 2 - ![]() , таблице 3 -
, таблице 3 - ![]() , таблице 4 -
, таблице 4 - ![]() . Точные значения коэффициентов
. Точные значения коэффициентов ![]() находятся по формулам (38), (39), (40); приближенные
находятся по формулам (38), (39), (40); приближенные ![]() по формуле (31), погрешность по формуле:
по формуле (31), погрешность по формуле:
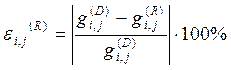 (43)
(43)
при этом при определении ![]() коэффициент
коэффициент ![]() был принят равным нулю (система без демпфирования). Значения коэффициентов передаточных матриц в таблицах найдены при нескольких значениях безразмерного параметра
был принят равным нулю (система без демпфирования). Значения коэффициентов передаточных матриц в таблицах найдены при нескольких значениях безразмерного параметра ![]() (второй столбец таблиц) в окрестности первых трех резонансов, антирезонансов и в промежуточных точках. Если значение параметра, соответствует частоте резонанса или антирезонанса, то это указывается в первых столбцах таблиц буквами «P» или «А». Число тонов колебаний
(второй столбец таблиц) в окрестности первых трех резонансов, антирезонансов и в промежуточных точках. Если значение параметра, соответствует частоте резонанса или антирезонанса, то это указывается в первых столбцах таблиц буквами «P» или «А». Число тонов колебаний ![]() , учитываемых при вычислениях, менялось от 1 до 50, оно указано во второй строке заголовка таблиц. В строках таблиц указаны значения погрешностей в процентах - без скобок при вычислении коэффициентов передаточных матриц без учета остаточной податливости, в скобках с учетом. Для сокращения размеров таблиц и наглядности погрешности менее 0,01 % заменены на нулевые значения, если значение погрешности превышает 100 % (это возможно при расчетах с без учета остаточных податливостей в окрестности антирезонанса) значение заменяется на «>100»). Если значение число тонов колебаний не достаточно (частота наивысшего учитываемого тона меньше частоты, при которой производится расчет) в ячейке ставится прочерк.
, учитываемых при вычислениях, менялось от 1 до 50, оно указано во второй строке заголовка таблиц. В строках таблиц указаны значения погрешностей в процентах - без скобок при вычислении коэффициентов передаточных матриц без учета остаточной податливости, в скобках с учетом. Для сокращения размеров таблиц и наглядности погрешности менее 0,01 % заменены на нулевые значения, если значение погрешности превышает 100 % (это возможно при расчетах с без учета остаточных податливостей в окрестности антирезонанса) значение заменяется на «>100»). Если значение число тонов колебаний не достаточно (частота наивысшего учитываемого тона меньше частоты, при которой производится расчет) в ячейке ставится прочерк.
Таблица 2. Значения погрешностей при определении ![]() без учета и с учетом остаточной податливости при отсутствии диссипации в системе.
без учета и с учетом остаточной податливости при отсутствии диссипации в системе.
|
| Значение погрешности | |||||
|
| r=1 | r=3 | r=5 | r=10 | r=20 | r=50 |
| 0 | 2.93 (0) | 0.14 (0) | 0.03 (0) | 0 (0) | 0 (0) | 0 (0) |
Р | 1.875 | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
| 2.905 | - | 0.85 (0) | 0.19 (0) | 0.02 (0) | 0 (0) | 0 (0) |
А | 3.141 | - - | >100 (25.12) | >100 (0.8) | 64.65 (0) | 8.05 (0) | 0.49 (0) |
| 4.306 | - - | 2.75 (0.04) | 0.6 (0) | 0.08 (0) | 0 (0) | 0 (0) |
Р | 4.694 | - - | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
| 5.884 | - - | 7.34 (0.41) | 1.56 (0.01) | 0.2 (0) | 0.02 (0) | 0 (0) |
А | 7.068 | - - | >100 (>100) | >100 (54.56) | >100 (0.45) | 51.3 (0) | 3.11 (0) |
| 7.461 | - - | 16.68 (2.49) | 3.23 (0.07) | 0.4 (0) | 0.05 (0) | 0 (0) |
Р | 7.854 | - - | 0.02 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
| 9.027 | - - | - - | 5.82 (0.26) | 0.71 (0) | 0.09 (0) | 0 (0) |
А | 10.2 | - - | - - | >100 (44.77) | 71.94 (0.34) | 8.92 (0) | 0.5 (0) |
Таблица 3. Значения погрешностей при определении ![]() без учета и с учетом остаточной податливости при отсутствии диссипации в системе.
без учета и с учетом остаточной податливости при отсутствии диссипации в системе.
|
| Значение погрешности | |||||
|
| r=1 | r=3 | r=5 | r=10 | r=20 | r=50 |
| 0 | 10.92 (0) | 1.39 (0) | 0.51 (0) | 0.13 (0) | 0.03 (0) | 0 (0) |
Р | 1.875 | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
| 2.51 | - - | 4.87 (0) | 1.78 (0) | 0.44 (0) | 0.11 (0) | 0.01 (0) |
А | 3.15 | - - | >100 (2.75) | 78.13 (0.14) | 69.48 (0) | 16.88 (0) | 2.23 (0) |
| 3.92 | - - | 10.36 (0.09) | 3.76 (0) | 0.94 (0) | 0.23 (0) | 0.03 (0) |
Р | 4.694 | - - | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
| 5.49 | - - | 21.67 (0.73) | 7.69 (0.04) | 1.91 (0) | 0.46 (0) | 0.06 (0) |
А | 6.28 | - - | >100 (>100) | >100 (3.98) | >100 (0.39) | >100 (0) | 23.49 (0) |
| 7.07 | - - | 38.59 (3.74) | 12.91 (0.17) | 3.19 (0) | 01.77 (0) | 0.1 (0) |
Р | 7.854 | - - | 0.04 (0) | 0.01 (0) | 0 (0) | 0 (0) | 0 (0) |
| 8.64 | - - | - - | 19.61 (0.58) | 4.77 (0) | 1.16 (0) | 0.15 (0) |
А | 9.42 | - - | - - | >100 (>100) | >100 (2.85) | >100 (0.04) | 33.85 (0) |
Таблица 4. Значения погрешностей при определении ![]() без учета и с учетом остаточной податливости при отсутствии диссипации в системе.
без учета и с учетом остаточной податливости при отсутствии диссипации в системе.
|
| Значение погрешности | |||||
|
| r=1 | r=3 | r=5 | r=10 | r=20 | r=50 |
| 0 | 38.44 (0) | 13.04 (0) | 7.7 (0) | 3.66 (0) | 1.63 (0) | 0.42 (0) |
Р | 1.875 | 0.01 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
| 2.120 | - - | 22.57 (0.01) | 13.33 (0) | 6.33 (0) | 2.82 (0) | 0.73 (0) |
А | 2.360 | - - | >100 (0.95) | >100 (0.08) | >100 (0) | >100 (0) | 42.78 (0) |
| 3.530 | - - | 30.91 (0.11) | 18.21 (0) | 8.64 (0) | 3.84 0 | 1 0 |
Р | 4.694 | - - | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
| 5.070 | - - | 40.81 (0.64) | 23.79 (0.05) | 11.28 (0) | 5.01 (0) | 1.31 (0) |
А | 5.450 | - - | >100 (12.59) | >100 (1.01) | >100 (0.03) | 72.82 (0) | 18.95 (0) |
| 6.650 | - - | 67.06 (3.27) | 37.95 (0.25) | 17.91 (0) | 7.96 (0) | 2.07 (0) |
Р | 7.854 | - - | 0.09 (0) | 0.05 (0) | 0.02 (0) | 0 (0) | 0 (0) |
| 8.240 | - - | - - | 42.94 (0.67) | 20.09 (0.02) | 8.93 (0) | 2.32 (0) |
А | 8.550 | - - | - - | >100 (5.24) | >100 (0.16) | 59.82 (0) | 15.57 (0) |
Результаты расчетов, записанные в таблицах 2-4, показывают, что наибольшие погрешности возникают при определении коэффициента ![]() . Для всех рассмотренных коэффициентов наибольшие погрешности присущи областям антирезонансов. Учет остаточной податливости приводит к значительному повышению точности определения коэффициентов. Если без учета остаточной податливости для определения коэффициентов передаточной матрицы с приемлемой точностью в частотном диапазоне от 0 до третьей собственной частоты может потребоваться порядка 20 – 50 тонов колебаний, то при учете статической поправки достаточно 5-10 тонов.
. Для всех рассмотренных коэффициентов наибольшие погрешности присущи областям антирезонансов. Учет остаточной податливости приводит к значительному повышению точности определения коэффициентов. Если без учета остаточной податливости для определения коэффициентов передаточной матрицы с приемлемой точностью в частотном диапазоне от 0 до третьей собственной частоты может потребоваться порядка 20 – 50 тонов колебаний, то при учете статической поправки достаточно 5-10 тонов.
5.Анализ точности вычисления коэффициентов при наличии демпфирования
Проанализируем теперь точность определения коэффициентов без учета и с учетом статической поправки для консольной балки при наличии демпфирования. Для этого сравним погрешности при вычислении амплитудно частотной и фазо частотной характеристик при тех же значениях частот, что и ранее. Коэффициент демпфирования возьмем равным ![]() .
.
Взяв достаточно большое количество тонов колебаний (n=100), посчитаем коэффициенты динамической податливости для мнимой и действительной частей по формулам (24) и (25) и примем полученные значения за точные. Расчет амплитуды и фазы осуществляется по формулам
![]() (44)
(44)
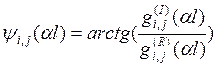 (45)
(45)
Погрешности определения амплитуды и фазы
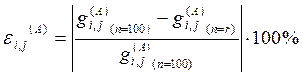 (46)
(46)
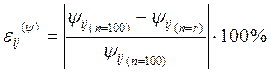 (47)
(47)
Результаты расчетов погрешностей амплитуды при различном числе учитываемых тонов ![]() даны в таблицах 5, 7, 9, фазы - в таблицах 6, 8, 10..
даны в таблицах 5, 7, 9, фазы - в таблицах 6, 8, 10..
Таблица 5. Значения погрешности при определении амплитуды ![]() без учета и с учетом остаточной податливости для системы с демпфированием.
без учета и с учетом остаточной податливости для системы с демпфированием.
|
| Значение погрешности | |||||
|
| r=1 | r=3 | r=5 | r=10 | r=20 | r=50 |
| 0
| 2.93 (0) | 0.14 (0) | 0.03 (0) | 0 (0) | 0 (0) | 0 (0) |
Р
| 1.875
| 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
| 2.905
| - - | 0.84 (0) | 0.19 (0) | 0.02 (0) | 0 (0) | 0 (0) |
А | 3.141
| - - | 1.64 (0.03) | 0.29 (0) | 0.03 (0) | 0 (0) | 0 (0) |
| 4.306
| - - | 2.13 (0.03) | 0.47 (0.01) | 0.06 (0) | 0 (0) | 0 (0) |
Р
| 4.694
| - - | 0.05 (0) | 0.01 (0) | 0 (0) | 0 (0) | 0 (0) |
| 5.884
| - - | 5.34 (0.42) | 1.14 (0.13) | 0.14 (0.02) | 0.02 (0) | 0 (0) |
А
| 7.068
| - - | 6.54 (1.65) | 1.31 (0.32) | 0.16 (0.04) | 0.02 (0) | 0 (0) |
| 7.461
| - - | 3.63 (1.76) | 0.73 (0.23) | 0.09 (0.03) | 0.01 (0) | 0 (0) |
Р
| 7.854
| - - | 2.67 (2.17) | 0.6 (0.24) | 0.07 (0.03) | 0 (0) | 0 (0) |
| 9.027
| - - | - - | 1.25 (0.84) | 0.16 (0.1) | 0.02 (0.01) | 0 (0) |
Таблица 6. Значения погрешности при определении фазы ![]() без учета и с учетом остаточной податливости для системы с демпфированием.
без учета и с учетом остаточной податливости для системы с демпфированием.
|
| Значение погрешности | |||||
|
| r=1 | r=3 | r=5 | r=10 | r=20 | r=50 |
| 0
| 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
Р | 1.875
| 0.07 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
| 2.905
| - - | 2.6 (0) | 0.58 (0) | 0.07 (0) | 0 (0) | 0 (0) |
А | 3.141
| - - | 7.19 (0.09) | 1.61 (0.04) | 0.2 (0) | 0.03 (0) | 0 (0) |
| 4.306
| - - | 2.19 (0.05) | 0.48 (0.02) | 0.06 (0) | 0 (0) | 0 (0) |
Р | 4.694
| - - | 0.9 (0.02) | 0.2 (0) | 0.02 (0) | 0 (0) | 0 (0) |
| 5.884
| - - | 13 (0.52) | 2.83 (0.31) | 0.36 (0.04) | 0.04 (0) | 0 (0) |
А | 7.068
| - - | 20.32 (2.45) | 4.3 (1) | 0.54 (0.13) | 0.07 (0.02) | 0 (0) |
| 7.461
| - - | 18.89 (3.04) | 3.87 (1.12) | 0.49 (0.15) | 0.06 (0.02) | 0 (0) |
Р | 7.854
| - - | 19.29 (3.89) | 3.86 (1.37) | 0.48 (0.18) | 0.06 (0.02) | 0 (0) |
| 9.027
| - - | - - | 7.02 (4.37) | 0.87 (0.58) | 0.11 (0.07) | 0 (0) |
Таблица 7. Значения погрешности при определении амплитуды ![]() без учета и с учетом остаточной податливости для системы с демпфированием.
без учета и с учетом остаточной податливости для системы с демпфированием.
|
| Значение погрешности | |||||
|
| r=1 | r=3 | r=5 | r=10 | r=20 | r=50 |
| 0
| 10.92 (0) | 1.39 (0) | 0.51 (0) | 0.13 (0) | 0.03 (0) | 0 (0) |
Р
| 1.875
| 0.02 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
- | 2.51
| - - | 4.81 (0.01) | 1.76 (0) | 0.44 (0) | 0.11 (0) | 0.01 (0) |
А
| 3.15
| - - | 22.62 (0.02) | 1.42 (0.03) | 0.48 (0) | 0.17 (0) | 0.02 (0) |
|
| - - | 10.31 (0.15) | 3.75 (0.08) | 0.94 (0.02) | 0.23 (0) | 0.03 (0) |
Р
| 4.694
| - - | 0.84 (0.01) | 0.32 (0.01) | 0.08 (0) | 0.02 (0) | 0 (0) |
|
| - - | 13.05 (0.84) | 4.48 (0.38) | 1.09 (0.1) | 0.26 (0.02) | 0.03 (0) |
А
| 6.28
| - - | 12.09 (1.05) | 1.75 (0.04) | 0.14 (0) | 0.02 (0) | 0 (0) |
| 7.07
| - - | 17.84 (2.44) | 7.44 (1.91) | 1.98 (0.51) | 0.49 (0.12) | 0.06 (0.02) |
Р
| 7.854
| - - | 12.63 (1.72) | 4.82 (1.91) | 1.28 (0.5) | 0.32 (0.12) | 0.04 (0.02) |
| 8.64
| - - | - - | 2.99 (2.14) | 0.89 (0.55) | 0.23 (0.13) | 0.03 (0.02) |
Таблица 8. Значения погрешности при определении фазы ![]() без учета и с учетом остаточной податливости для системы с демпфированием.
без учета и с учетом остаточной податливости для системы с демпфированием.
|
| Значение погрешности | |||||
|
| r=1 | r=3 | r=5 | r=10 | r=20 | r=50 |
| 0
| 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
Р
| 1.875
| 0.28 (0) | 0.04 (0) | 0.01 (0) | 0 (0) | 0 (0) | 0 (0) |
| 2.51
| - - | 8.95 (0.02) | 3.36 (0.01) | 0.85 (0) | 0.21 (0) | 0.03 (0) |
А | 3.15
| - - | >100 (0.33) | >100 (0.18) | >100 (0.05) | >100 (0.01) | 0.15 (0) |
| 3.92
| - - | 6.84 (0.13) | 2.33 (0.05) | 0.56 (0.01) | 0.14 (0) | 0.02 (0) |
Р
| 4.694
| - - | >100 (0.08) | 0.86 (0.04) | 0.21 (0.01) | 0.05 (0) | 0 (0) |
| 5.49
| - - | 22.48 (1.24) | 8.57 (0.76) | 2.2 (0.2) | 0.54 (0.05) | 0.07 (0) |
А | 6.28
| - - | 40.61 (4.32) | 15.12 (2.26) | 3.8 (0.59) | 0.92 (0.14) | 0.12 (0.02) |
| 7.07
| - - | >100 (4.49) | >100 (1.99) | 2.13 (0.52) | 0.51 (0.13) | 0.07 (0.02) |
Р
| 7.854 7 | - - | 25.43 (6.28) | 7.91 (2.7) | 1.88 (0.7) | 0.45 (0.17) | 0.06 (0.02) |
| 8.64
| - - | - - | 12.74 (6.45) | 3.06 (1.68) | 0.74 (0.41) | 0.1 (0.05) |
Таблица 9. Значения погрешности при определении амплитуды ![]() без учета и с учетом остаточной податливости для системы с демпфированием.
без учета и с учетом остаточной податливости для системы с демпфированием.
|
| Значение погрешности | |||||
|
| r=1 | r=3 | r=5 | r=10 | r=20 | r=50 |
| 0
| 38.44 (0) | 13.04 (0) | 7.7 (0) | 3.66 (0) | 1.63 (0) | 0.42 (0) |
Р
| 1.875
| 0.12 (0) | 0.04 (0) | 0.03 (0) | 0.01 (0) | 0 (0) | 0 (0) |
| 2.12
| - - | 22.1 (0.03) | 13.04 (0.02) | 6.19 (0.01) | 2.75 (0) | 0.72 (0) |
А | 2.360
| - - | >100 (0.18) | >100 (0.13) | 50.41 (0.06) | 16.15 (0.03) | 2.86 (0) |
| 3.53
| - - | 31 (0.37) | 18.27 (0.27) | 8.67 (0.13) | 3.86 (0.06) | 1 (0.02) |
Р
| 4.694
| - - | 4.78 (0.18) | 3 (0.15) | 1.49 (0.08) | 0.68 (0.03) | 0.18 (0) |
| 5.07
| - - | 14.74 (0.58) | 7.35 (0.34) | 2.98 (0.16) | 1.21 (0.07) | 0.3 (0.02) |
А | 5.450
| - - | 22.99 (1.64) | 5.08 (0.79) | 0.96 (0.38) | 1.2 (0.16) | 0.43 (0.04) |
| 6.65
| - - | 56.82 (9.26) | 35.29 (7.03) | 17.22 (3.43) | 7.74 (1.53) | 2.03 (0.4) |
Р
| 7.854
| - - | 40.62 (13.51) | 25.19 (10.49) | 12.65 (5.08) | 5.77 (2.25) | 1.52 (0.58) |
| 8.24
| - - | - - | 24.76 (13.36) | 12.82 (6.42) | 5.91 (2.83) | 1.57 (0.73) |
Таблица 10. Значения погрешности при определении фазы ![]() коэффициента без учета и с учетом остаточной податливости для системы с демпфированием.
коэффициента без учета и с учетом остаточной податливости для системы с демпфированием.
|
| Значение погрешности | |||||
|
| r=1 | r=3 | r=5 | r=10 | r=20 | r=50 |
| 0
| 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
Р
| 1.875
| 1.44 (0.02) | 0.48 (0) | 0.28 (0) | 0.13 (0) | 0.06 (0) | 0.02 (0) |
| 2.12
| - - | 23.76 (0.04) | 15.16 (0.03) | 7.66 (0.02) | 3.52 (0) | 0.94 (0) |
А
| 2.360
| - - | 83.45 (0.59) | 71.69 (0.44) | 49.82 (0.22) | 27.3 (0.1) | 7.87 (0.03) |
| 3.53
| - - | 13.81 (0.19) | 6.92 (0.09) | 2.94 (0.04) | 1.24 (0.02) | 0.31 (0) |
Р | 4.694
| - - | 9.79 (0.35) | 5.62 (0.26) | 2.62 (0.13) | 1.16 (0.06) | 0.3 (0.01) |
| 5.07
| - - | 29.87 (1.67) | 18.42 (1.26) | 9.05 (0.61) | 4.09 (0.27) | 1.07 (0.07) |
А
| 5.450
| - - | 56.08 (4.19) | 35.7 (3.04) | 17.34 (1.49) | 7.66 (0.67) | 1.98 (0.17) |
| 6.65
| - - | 79.69 (6.00) | 29.77 (3.49) | 10.96 (1.71) | 4.37 (0.78) | 1.07 (0.2) |
Р
| 7.854
| - - | >100 (10.05) | 23.74 (6.01) | 9.54 (3.01) | 3.92 (1.38) | 0.98 (0.36) |
| 8.24
| - - | - - | >100 (7.82) | 10.53 (3.97) | 4.33 (1.83) | 1.08 (0.48) |
Анализ результатов расчета коэффициентов динамической податливости в системе с наличием демпфирования показывает, что учет остаточной податливости приводит к существенному уточнению и амплитуды и фазы. Как и в случае отсутствия демпфирования с увеличением значения безразмерного параметра ![]() отмечается повышение погрешности, погрешность при этом нарастает в меньшей степени, чем в системе с демпфированием. В областях близких к антирезонансам погрешности по фазе получаются существенно больше, чем погрешности по амплитуде.
отмечается повышение погрешности, погрешность при этом нарастает в меньшей степени, чем в системе с демпфированием. В областях близких к антирезонансам погрешности по фазе получаются существенно больше, чем погрешности по амплитуде.
Таким образом, во всех случаях статическая поправка, предложенная в настоящей статье, дает заметное увеличение точности вычислений. Если при этом выполняется частотный критерий – частота последнего учитываемого тона колебаний превышает верхнюю границу частотного диапазона, то точность вычислений оказывается вполне удовлетворительной.
Список литературы
1. Гусев А.С. Вероятностные методы в механике машин и конструкций. М.: Изд-во МГТУ им. Н.Э. Баумана, 2009. 223 с.
2. Светлицкий В.А. Статистическая механика и теория надежности. М.: Изд-во МГТУ им. Баумана, 2002. 504 с.
3. Вибрации в технике. Справочник. В 6 т. Т. 1 / под ред. В.Н. Челомея. М.: Машиностроение. 352 с.
4. Прочность. Устойчивость. Колебания. Справочник. В 3 т. Т. 3 /под ред. И.А. Биргера и Я.Г. Пановко. М.: Машиностроение, 1968. 507 с.
5. Ильин М.М., Колесников К.С., Саратов Ю.С. Теория колебаний. М.: Изд-во МГТУ им. Н.Э. Баумана, 2003. 271 с.
6. Крейг Р., Чжан К. Методы свободных границ для связывания субконструкций при исследовании динамики // Ракетная техника и космонавтика (русск. перевод журнала American Institute of Aeronautics and Astronautics). 1976. Т. 14, № 11. [Craig R., Chang C.-J. Free-interface methods of substructure coupling for dynamic analysis // AIAA Journal. 1976. Vol. 14, no. 11. P. 1633-1635. DOI: 10.2514/3.7264 ].
7. Тимошенко С.П. Колебания в инженерном деле. М.: Наука, 1967. 444 с.
Публикации с ключевыми словами: динамика, передаточная матрица, конечный элемент, демпфирование, динамическая податливость, стационарный случайный процесс
Публикации со словами: динамика, передаточная матрица, конечный элемент, демпфирование, динамическая податливость, стационарный случайный процесс
Смотри также:
- Применение полимерных композиционных материалов в системах подрессоривания колесных машин
- Методология моделирования трехмерных механических систем с помощью универсальных программных комплексов анализа
- Моделировние динамики НПА от рукоятки 3D Connexion Space Navigator под управлением САУ в пакете MatLab/Simulink
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



