научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 02, февраль 2013
DOI: 10.7463/0213.0533324
УДК 681.5.013
Россия, МГТУ им. Н.Э. Баумана
Введение
Регуляторы, обеспечивающие устойчивое и качественное управление при изменении параметров объекта в достаточно широких пределах, получили название робастных. Интерес к робастному управлению существенно возрос после появления статьи В.Л. Харитонова [1] об устойчивости интервальных полиномов, т.е. полиномов, коэффициенты которых могут изменяться в заданных пределах. Вслед за этой статьей появилось большое число публикаций по робастной устойчивости. Отметим, однако, что робастная система должна быть не только устойчивой, но и должна обладать заданным качеством при любых допустимых значениях параметров объекта.
В работах [2, 3] отмечалось, что многие современные методы синтеза регуляторов не получили широкого практического применения. Это объясняется рядом причин, среди которых: отсутствие простой и понятной связи между минимизируемым функционалом и применяемыми на практике показателями качества, чувствительность системы к изменениям параметров объекта, необоснованная сложность синтезированного регулятора. В то же время в промышленности востребованы простые регуляторы низкого порядка (такие как ПИ, ПД, ПИД).
Робастное качество систем управления можно оценить показателями, которые рассматривались в [4–8], и имеют простую зависимость от коэффициентов характеристического полинома. Простые показатели качества характеристических полиномов предложил P. Naslin еще в 1963 г. [4], однако эта работа осталась практически незамеченной. Начиная с 1965 г. вопросами построения простых критериев устойчивости и качества по коэффициентам полинома занимался В.С. Воронов, но ранние его работы остались неизвестными, поскольку были опубликованы в труднодоступных изданиях. В сжатом виде полученные В.С. Вороновым основные результаты изложены в [5]. Аналогичные результаты приведены в работах Н.И. Соколова и А.В. Липатова, обобщенных в [6].
Приведем основные результаты, следуя работе [5]. Рассмотрим непрерывную линейную систему управления с характеристическим полиномом
![]() . (1)
. (1)
Предположим, что все коэффициенты полинома имеют одинаковый знак (пусть они положительны), что является простейшим необходимым условием устойчивости.
Устойчивость и качество системы управления с характеристическим полиномом (1) можно оценить с помощью следующих показателей [5]:
1) приближенные сопрягающие частоты
![]() ;
;
2) показатели (меры) качества
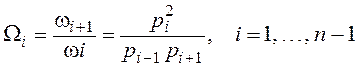 ;
;
3) показатели (меры) устойчивости
 .
.
Выполнение неравенств ![]() является необходимым условием устойчивости, а простейшее достаточное условие устойчивости запишется в виде
является необходимым условием устойчивости, а простейшее достаточное условие устойчивости запишется в виде
![]() , (2)
, (2)
где ![]() – вещественный корень уравнения
– вещественный корень уравнения ![]() . Условие (2) будет всегда выполняться, если
. Условие (2) будет всегда выполняться, если
![]() . (3)
. (3)
Таким образом, (3) – простейшее достаточное условие устойчивости, сформированное через показатели качества.
Для робастных систем условия (2) или (3) должны выполняться с запасом. В [5] такие условия с запасом рекомендуется принимать в виде
![]() , (4)
, (4)
![]() . (5)
. (5)
Условие ![]() является достаточным для того, чтобы все корни полинома были вещественными. В [5, 6] приведены также и более сложные достаточные условия устойчивости, практически приближающиеся к необходимому и достаточному условию. Однако наиболее удобны для синтеза самые простые условия вида (2)–(5), поэтому ограничимся их рассмотрением.
является достаточным для того, чтобы все корни полинома были вещественными. В [5, 6] приведены также и более сложные достаточные условия устойчивости, практически приближающиеся к необходимому и достаточному условию. Однако наиболее удобны для синтеза самые простые условия вида (2)–(5), поэтому ограничимся их рассмотрением.
Связь между ![]() и другими показателями качества исследовалась в [6, 7]. Значения
и другими показателями качества исследовалась в [6, 7]. Значения ![]() определяют качество переходных процессов. Уменьшение этих показателей приводит к увеличению перерегулирования и уменьшению запасов устойчивости. Выполнение для некоторого
определяют качество переходных процессов. Уменьшение этих показателей приводит к увеличению перерегулирования и уменьшению запасов устойчивости. Выполнение для некоторого ![]() неравенства
неравенства ![]() является достаточным условием наличия комплексно сопряженных корней (это следует из [6, теорема 5.2]). Малое значение
является достаточным условием наличия комплексно сопряженных корней (это следует из [6, теорема 5.2]). Малое значение ![]() обычно свидетельствует о колебательности переходного процесса, при этом, чем больше
обычно свидетельствует о колебательности переходного процесса, при этом, чем больше ![]() , тем выше частота колебаний, которую можно приближенно оценить величиной
, тем выше частота колебаний, которую можно приближенно оценить величиной ![]() . Качество системы определяется в большей степени первыми двумя-тремя значениями
. Качество системы определяется в большей степени первыми двумя-тремя значениями ![]() , поэтому при синтезе регуляторов низкого порядка следует корректировать именно эти значения. Некоторые преимущества дает задание равных или примерно равных значений
, поэтому при синтезе регуляторов низкого порядка следует корректировать именно эти значения. Некоторые преимущества дает задание равных или примерно равных значений ![]() .
.
Рассмотрим теперь семейство полиномов (1), коэффициенты которых удовлетворяют неравенствам ![]() ,
, ![]() . Условия вида (2)–(5) для такого семейства получаем заменой
. Условия вида (2)–(5) для такого семейства получаем заменой ![]() и
и ![]() на значения
на значения
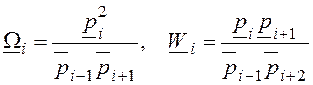 . (6)
. (6)
Значения ![]() показателей устойчивости можно получить, рассматривая четыре полинома Харитонова, которые дают наихудшие (с точки зрения устойчивости) сочетания коэффициентов. А для показателей качества
показателей устойчивости можно получить, рассматривая четыре полинома Харитонова, которые дают наихудшие (с точки зрения устойчивости) сочетания коэффициентов. А для показателей качества ![]() наихудшими являются два полинома, в которых чередуются минимальные и максимальные значения коэффициентов.
наихудшими являются два полинома, в которых чередуются минимальные и максимальные значения коэффициентов.
В статье предложен новый подход к синтезу регуляторов, основанный на использовании рассмотренных выше показателей. На конкретных примерах показано, что этот подход позволяет синтезировать регуляторы минимального порядка, обеспечивающие заданное качество системы управления при неопределенности параметров объекта.
1 Постановка задачи
Рассмотрим линейную одномерную систему, структурная схема которой показана на рисунке. Объект описывается дробно-рациональной передаточной функцией ![]() , а передаточную функцию регулятора зададим в виде
, а передаточную функцию регулятора зададим в виде ![]() , где
, где ![]() ,
, ![]() . Примем также
. Примем также ![]() . Характеристический полином замкнутой системы имеет вид
. Характеристический полином замкнутой системы имеет вид
![]() . (7)
. (7)
Как правило, корректирующие свойства регулятора определяются коэффициентами числителя его передаточной функции. Поэтому будем искать коэффициенты полинома ![]() , предполагая, что полином
, предполагая, что полином ![]() задан исходя из условий обеспечения заданного порядка астатизма и фильтрующих свойств регулятора. Подбором значений неизвестных параметров регулятора
задан исходя из условий обеспечения заданного порядка астатизма и фильтрующих свойств регулятора. Подбором значений неизвестных параметров регулятора ![]() можно добиться заданных значений
можно добиться заданных значений ![]() показателей. В зависимости от того, какие показатели используются при синтезе, возможны следующие постановки задачи.
показателей. В зависимости от того, какие показатели используются при синтезе, возможны следующие постановки задачи.

Рисунок – Структурная схема системы управления
Задача 1. Найти значения параметров регулятора, при которых показатели качества ![]() принимают заданные значения.
принимают заданные значения.
Значения ![]() не изменятся, если каждый из коэффициентов
не изменятся, если каждый из коэффициентов ![]() полинома (1) умножить на
полинома (1) умножить на ![]() . Число
. Число ![]() задает временной масштаб, но не влияет на качество переходных процессов (чем меньше
задает временной масштаб, но не влияет на качество переходных процессов (чем меньше ![]() , тем быстрее протекают процессы в системе). Поэтому при синтезе систем заданного быстродействия следует добавить показатель, оценивающий быстродействие системы. В качестве такого показателя можно использовать значение
, тем быстрее протекают процессы в системе). Поэтому при синтезе систем заданного быстродействия следует добавить показатель, оценивающий быстродействие системы. В качестве такого показателя можно использовать значение ![]() .
.
Задача 2. Найти значения параметров регулятора, при которых приближенная сопрягающая частота ![]() и показатели качества
и показатели качества ![]() принимают заданные значения.
принимают заданные значения.
Для следящих систем важным показателем является точность отработки задающего воздействия. Ошибка следящей системы определяется в значительной степени положением низкочастотной асимптоты логарифмической амплитудно-частотной характеристики разомкнутой системы. Передаточная функция разомкнутой системы равна ![]() . Низкочастотная асимптота однозначно задается значениями порядка астатизма
. Низкочастотная асимптота однозначно задается значениями порядка астатизма ![]() и низкочастотного коэффициента усиления (добротности)
и низкочастотного коэффициента усиления (добротности) ![]() . Для системы, имеющей порядок астатизма
. Для системы, имеющей порядок астатизма ![]() , коэффициенты
, коэффициенты ![]() полинома
полинома ![]() равны
равны ![]() , а
, а ![]() .
.
Задача 3. Найти значения параметров регулятора, при которых добротность ![]() и показатели качества
и показатели качества ![]() принимают заданные значения.
принимают заданные значения.
В результате расчета регулятора низкого порядка можно получить систему, которая не удовлетворяет некоторым требованиям либо даже окажется неустойчивой. Поэтому следует, начиная с минимально возможного порядка, последовательно повышать порядок регулятора до тех пор, пока не будут выполнены все требования. Такая процедура позволяет синтезировать регуляторы минимального порядка.
2 Решение задачи
В приведенных постановках решение задачи синтеза сводится к решению системы нелинейных алгебраических уравнений относительно неизвестных параметров регулятора. Решение задачи 2, а также решение задач 1 и 3 при ![]() (т.е. при
(т.е. при ![]() ) можно представить в виде конечных формул. Решение задач 1 и 3 при
) можно представить в виде конечных формул. Решение задач 1 и 3 при ![]() следует производить итерационным методом. Уравнения для итераций можно сформировать таким образом, что при любом
следует производить итерационным методом. Уравнения для итераций можно сформировать таким образом, что при любом ![]() они будут содержать две неизвестные при решении задачи 1 и одну неизвестную при решении задачи 3.
они будут содержать две неизвестные при решении задачи 1 и одну неизвестную при решении задачи 3.
Запишем соотношение (7) через коэффициенты полиномов:
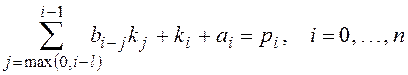 .
.
Если коэффициенты ![]() известны, то параметры регулятора можно найти с помощью рекуррентных формул
известны, то параметры регулятора можно найти с помощью рекуррентных формул
 . (8)
. (8)
Решение задачи 1. Если известны ![]() и
и ![]() , то коэффициенты
, то коэффициенты ![]() можно найти по формулам
можно найти по формулам
![]() . (9)
. (9)
Таким образом, решение задачи сводится к нахождению ![]() и
и ![]() из уравнений
из уравнений
 , (10)
, (10)
где значения ![]() рассчитываем по формулам (9), (8). Если
рассчитываем по формулам (9), (8). Если ![]() , то уравнения (10) превращаются в равенства
, то уравнения (10) превращаются в равенства ![]() ,
, ![]() . Эти же значения рекомендуется задавать в качестве начальных при итерационном решении уравнений (10).
. Эти же значения рекомендуется задавать в качестве начальных при итерационном решении уравнений (10).
Решение задачи 2. Если известно значение ![]() , то коэффициенты
, то коэффициенты ![]() можно найти по формулам
можно найти по формулам
 (11)
(11)
Уравнение относительно ![]() запишется в виде
запишется в виде
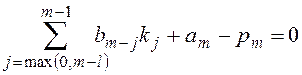 , (12)
, (12)
где значения ![]() находим из (11), (8). Уравнение (12) является линейным и может быть решено следующим образом. Задав
находим из (11), (8). Уравнение (12) является линейным и может быть решено следующим образом. Задав ![]() , вычислим по формулам (11), (8), (12) левую часть (невязку)
, вычислим по формулам (11), (8), (12) левую часть (невязку) ![]() уравнения (12). Аналогичным образом вычислим невязку
уравнения (12). Аналогичным образом вычислим невязку ![]() этого уравнения при
этого уравнения при ![]() . Тогда решение уравнения (12) будет
. Тогда решение уравнения (12) будет ![]() . Зная
. Зная ![]() , из (11) и (8) находим искомые параметры регулятора.
, из (11) и (8) находим искомые параметры регулятора.
Решение задачи 3. Если известно значение ![]() , то коэффициенты
, то коэффициенты ![]() можно найти по формулам
можно найти по формулам
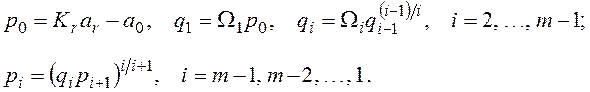 (13)
(13)
Уравнение относительно ![]() запишется в виде (12), где значения
запишется в виде (12), где значения ![]() находим из (13), (8). В качестве начального значения для итераций рекомендуется задавать
находим из (13), (8). В качестве начального значения для итераций рекомендуется задавать ![]() . Решив уравнение (12), находим параметры регулятора из (13), (8).
. Решив уравнение (12), находим параметры регулятора из (13), (8).
3 Примеры
Все примеры были реализованы и решены с помощью программного комплекса (ПК) "МВТУ" [9,10], который является аналогом пакета Simulink, входящего в состав системы MATLAB. Модели в ПК "МВТУ" формируются в виде структурных схем, состоящих из типовых блоков, соединенных линиями связи (в том числе и векторными). Встроенный паскале-подобный язык программирования позволяет в удобном виде задавать дифференциальные и алгебраические уравнения. С помощью этого языка были записаны уравнения синтеза. Для решения этих уравнений применялись реализованные в ПК "МВТУ" методы Ньютона-Рафсона и Бройдена.
Пример 1. Объект задан передаточной функцией
 . (14)
. (14)
Проведем синтез ПИ-регулятора с передаточной функцией ![]() на основе заданных значений
на основе заданных значений ![]() и
и ![]() . Результаты, полученные при
. Результаты, полученные при ![]() , представлены в таблице 1. Приведены следующие показатели:
, представлены в таблице 1. Приведены следующие показатели: ![]() – наиболее близкий к мнимой оси корень характеристического полинома,
– наиболее близкий к мнимой оси корень характеристического полинома, ![]() – время переходного процесса,
– время переходного процесса, ![]() – перерегулирование,
– перерегулирование, ![]() – запас устойчивости по фазе. Как меру робастности приводим
– запас устойчивости по фазе. Как меру робастности приводим ![]() – максимальное значение
– максимальное значение ![]() , при котором все объекты с параметрами, удовлетворяющими ограничениям
, при котором все объекты с параметрами, удовлетворяющими ограничениям ![]() ,
, ![]() , стабилизируются данным регулятором. Здесь
, стабилизируются данным регулятором. Здесь ![]() и
и ![]() – номинальные значения, приведенные в (14). В качестве времени переходного процесса принимаем минимальное время, по истечении которого ошибка при единичном входном воздействии не превышает 0,02. Добротность по ускорению
– номинальные значения, приведенные в (14). В качестве времени переходного процесса принимаем минимальное время, по истечении которого ошибка при единичном входном воздействии не превышает 0,02. Добротность по ускорению ![]() совпадает с коэффициентом
совпадает с коэффициентом ![]() регулятора.
регулятора.
При увеличении значений ![]() робастность системы повышается, что видно также по увеличению запаса по фазе и уменьшению перерегулирования, но некоторые другие показатели ухудшаются. Время
робастность системы повышается, что видно также по увеличению запаса по фазе и уменьшению перерегулирования, но некоторые другие показатели ухудшаются. Время ![]() сначала уменьшается, а затем увеличивается, что вполне объясняется характером изменения корня
сначала уменьшается, а затем увеличивается, что вполне объясняется характером изменения корня ![]() . Наиболее приемлемым является значение
. Наиболее приемлемым является значение ![]() , которое обеспечивает максимальную степень устойчивости
, которое обеспечивает максимальную степень устойчивости ![]() и компромисс между другими показателями.
и компромисс между другими показателями.
Таблица 1 – Результаты решения примера 1
|
|
|
| T | σ, % | Δφ, ° |
|
1,5 | 2,02 | 0,46, 0,59 |
| 32,9 | 75,7 | 15,0 | 1,12 |
2,0 | 2,00 | 0,20, 0,60 |
| 12,5 | 42,4 | 38,3 | 1,34 |
2,5 | 2,21 | 0,076, 0,45 |
| 16,6 | 25.0 | 52,9 | 1,49 |
3,0 | 2,39 | 0,035, 0,34 |
| 26,7 | 18,4 | 61,1 | 1,60 |
Пример 2. Объект задан передаточной функцией
 . (15)
. (15)
Необходимо найти регулятор минимального порядка, обеспечивающий время переходного процесса ![]() . Для обеспечения заданного быстродействия значение
. Для обеспечения заданного быстродействия значение ![]() должно быть не меньше
должно быть не меньше ![]() . А чтобы регулятор был робастным, значения
. А чтобы регулятор был робастным, значения ![]() должны быть достаточно большими. Потребуем, чтобы выполнялись неравенства
должны быть достаточно большими. Потребуем, чтобы выполнялись неравенства ![]() для
для ![]() и
и ![]() для
для ![]() . При синтезе задаем показатели
. При синтезе задаем показатели ![]() и
и ![]() , по которым находим параметры регулятора.
, по которым находим параметры регулятора.
Использование регуляторов 0-го и 1-го порядка не позволило обеспечить ![]() , поэтому остановимся на регуляторе 2-го порядка c передаточной функцией
, поэтому остановимся на регуляторе 2-го порядка c передаточной функцией
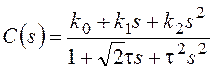 . (16)
. (16)
Знаменатель в (16) такой же, как у фильтра Баттерворта 2-го порядка, что позволяет обеспечить хорошую фильтрацию помех. Первоначально задаем ![]() . Принимая
. Принимая ![]() и рассчитав несколько вариантов, мы нашли значения
и рассчитав несколько вариантов, мы нашли значения ![]() ,
, ![]() , при которых требования выполняются с некоторым запасом. Оставляя неизменными эти значения, увеличиваем
, при которых требования выполняются с некоторым запасом. Оставляя неизменными эти значения, увеличиваем ![]() пока требования еще выполняются. В результате получили следующие значения параметров регулятора (16):
пока требования еще выполняются. В результате получили следующие значения параметров регулятора (16):
![]() . (17)
. (17)
Таблица 2 – Результаты решения примера 2
γ |
|
| η | T | σ, % |
1,0 |
| 2,80, 2,80, 2,31, 3,84, 2,05 | 1,24 | 1,75 | 14,3 |
1,5 |
| 3.32, 1,52, 6,00, 2,69, 2,22 | 0.81 | 3.75 | 19,7 |
2,0 |
| 3,77, 3,89, 0.43, 10,6, 2,00 | 0.30 | 12,8 | 70,4 |
Исследуем робастность синтезированной системы. Для этого предположим, что параметры объекта (15) является интервальными числами, удовлетворяющими ограничениям ![]() . Примем
. Примем ![]() ,
, ![]() , где
, где ![]() – номинальные значения, приведенные в (15). Для
– номинальные значения, приведенные в (15). Для ![]() и
и ![]() мы нашли значения параметров объекта, удовлетворяющие заданным ограничениям, при которых время переходного процесса
мы нашли значения параметров объекта, удовлетворяющие заданным ограничениям, при которых время переходного процесса ![]() принимает максимальное значение (для расчета использовался режим "Оптимизация" ПК "МВТУ"). Полученные результаты приведены в таблице 2, где
принимает максимальное значение (для расчета использовался режим "Оптимизация" ПК "МВТУ"). Полученные результаты приведены в таблице 2, где ![]() – степень устойчивости. Отметим, что максимальные значения
– степень устойчивости. Отметим, что максимальные значения ![]() были достигнуты в вершинных точках области допустимых значений параметров. Было найдено также максимальное значение
были достигнуты в вершинных точках области допустимых значений параметров. Было найдено также максимальное значение ![]() , при котором интервальный объект стабилизируется регулятором (16), (17).
, при котором интервальный объект стабилизируется регулятором (16), (17).
Пример 3. Рассмотрим построение робастного регулятора при интервальной неопределенности параметров объекта. Объект задан передаточной функцией
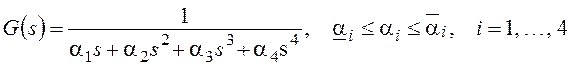 ,
,
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Требуется найти регулятор минимального порядка, обеспечивающий второй порядок астатизма и добротность по ускорению
. Требуется найти регулятор минимального порядка, обеспечивающий второй порядок астатизма и добротность по ускорению ![]() . Кроме этого потребуем, выполнения неравенств
. Кроме этого потребуем, выполнения неравенств ![]() для
для ![]() и неравенств
и неравенств ![]() для всех
для всех ![]() .
.
Второй порядок астатизма обеспечивает ПИ-регулятор, но он не позволяет обеспечить заданные требования даже при номинальных значениях параметров объекта. Поэтому будем использовать ПИД‑регулятор с передаточной функцией
 .
.
Представим нашу задачу как задачу математического программирования
 (18)
(18)
где ![]() и
и ![]() – минимальные значения соответствующих показателей в области допустимых значений параметров объекта. При
– минимальные значения соответствующих показателей в области допустимых значений параметров объекта. При ![]() значения
значения ![]() и
и ![]() можно рассчитать по формулам (6). Для этого достаточно найти значения
можно рассчитать по формулам (6). Для этого достаточно найти значения ![]() в двух точках области:
в двух точках области: ![]() и
и ![]() , а значения
, а значения ![]() – в четырех точках, соответствующих полиномам Харитонова. Этот же прием можно использовать и при малых значениях
– в четырех точках, соответствующих полиномам Харитонова. Этот же прием можно использовать и при малых значениях ![]() .
.
В результате решения задачи (18) с помощью ПК "МВТУ" получены значения параметров регулятора ![]() ,
, ![]() ,
, ![]() ,
, ![]() , при которых
, при которых ![]() ,
, ![]() ,
, ![]() . Для полученного регулятора с помощью поисковой оптимизации мы нашли наихудшие значения ряда показателей во всей допустимой области изменения параметров объекта. Результаты при номинальных, а также наиболее неблагоприятных сочетаниях параметров приведены в таблице 3. Наихудшие значения показателей выделены жирным шрифтом.
. Для полученного регулятора с помощью поисковой оптимизации мы нашли наихудшие значения ряда показателей во всей допустимой области изменения параметров объекта. Результаты при номинальных, а также наиболее неблагоприятных сочетаниях параметров приведены в таблице 3. Наихудшие значения показателей выделены жирным шрифтом.
Таблица 3 – Результаты решения примера 3
|
|
|
|
| η | T | σ, % |
| 1,87 | 2,51 | 1,87 | 4,70 | 0,501 | 7,51 | 35,5 |
| 1,81 | 3,78 | 1,11 | 3,81 | 0,440 | 4,17 | 49,0 |
| 1,81 | 3,78 | 1,64 | 3,00 | 0,436 | 4,38 | 36,2 |
| 1,81 | 2,08 | 1,61 | 3,10 | 0,405 | 8,43 | 34,6 |
| 1,95 | 1,81 | 1,72 | 3,52 | 0,406 | 10,4 | 40,6 |
| 1,95 | 3,32 | 1,15 | 3,33 | 0,495 | 5,31 | 62,6 |
Заключение
Использование рассмотренных показателей устойчивости и качества позволяет синтезировать регуляторы минимального порядка, обеспечивающие устойчивость и заданные динамические свойства системы управления при любых допустимых значениях параметров объекта. Простая связь этих показателей с другими показателями качества и коэффициентами характеристического полинома делает процедуру синтеза простой и понятной.
Список литературы
- Харитонов В.Л. Асимптотическая устойчивость семейства систем линейных дифференциальных уравнений //Дифференциальные уравнения. 1978. Т. 14, № 11. С. 2086-2088.
- Киселев О.Н., Поляк Б.Т. Синтез регуляторов низкого порядка по критерию H ¥ и по критерию максимальной робастности // Автоматика и телемеханика. 1999. № 3. С. 119-130.
- Гончаров В.И., Лиепиньш А.В., Рудницкий В.А. Синтез робастных регуляторов низкого порядка // Известия РАН. Теория и системы управления. 2001. № 4. С. 36-43.
- Naslin P. Polynomes normaux et critere algebrique d'amortissement // Automatisme. 1963. Vol. 8, no. 6. P. 215-233.
- Воронов В.С. Показатели устойчивости и качества робастных систем управления // Известия РАН. Теория и системы управления. 1995. № 6. С. 49-54.
- Системы автоматического управления объектами с переменными параметрами: Инженерные методы анализа и синтеза / Б.Н. Петров, Н.И. Соколов, А.В. Липатов, Л.А. Носов, Ф.Р. Садыков, Г.В. Серпионов, П.А. Фролов, Ш.Г. Альтшулер. М.: Машиностроение, 1986. 256 с.
- Скворцов Л.М., Федосов Б.Т. Об алгебраических критериях В.С. Воронова устойчивости и качества линейных систем. 2005. Режим доступа: http://model.exponenta.ru/bt/bt_00118.html (дата обращения 18.12.2012).
- Опейко О.Ф. Синтез линейной системы на основании упрощенной модели объекта // Автоматика и телемеханика. 2005. № 1. С. 29-36.
- Козлов О.С., Кондаков Д.Е., Скворцов Л.М., Тимофеев К.А., Ходаковский В.В. Программный комплекс "Моделирование в технических устройствах". 2005. Режим доступа: http://model.exponenta.ru/mvtu/20050615.html (дата обращения 18.12.2012).
- Козлов О.С., Скворцов Л.М. Исследование и проектирование автоматических систем с помощью программного комплекса "МВТУ" // Информационные технологии. 2006. № 8. C. 9-15.
Публикации с ключевыми словами: робастное управление, характеристический полином, показатели устойчивости и качества
Публикации со словами: робастное управление, характеристический полином, показатели устойчивости и качества
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



