научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2012
DOI: 10.7463/1212.0514343
УДК 006.91; 55.01.81
Россия, МГТУ им. Н.Э. Баумана
Введение
В условиях работы сложных технических объектов, таких как турбоагрегаты, гидроагрегаты, различные технологические линии и др., во время эксплуатации доступ к первичным преобразователям информационно-измерительных систем закрыт, и возможность метрологических работ появляется только при ремонте объекта. Межремонтный срок может быть от 2 до 5 лет и выполнить сроки межповерочных интервалов не представляется возможным. В связи с этим возникает проблема метрологического обеспечения измерительных каналов информационно-измерительных систем функционирующих в условиях эксплуатации объекта.
Для сложных технических систем важно обеспечить непрерывное информационно-метрологическое сопровождение в условиях эксплуатации для обеспечения аварийной защиты, диагностики и управления.
Встроенные фазохронометрические системы [1, 2, 3] функционируют в условиях
- необходимости обеспечения относительной погрешности измерения не более 5·10-4 % от номинальной длительности рабочего цикла функционирующего механизма (контролируемый параметр – интервалы времени),
- влияния неконтролируемых воздействий на объект в процессе эксплуатации (различные поля и механические воздействия),
- неконтролируемых воздействий влияющих величин на точность измерения,
- отсутствия возможности демонтажа встроенных блоков измерительной системы при многолетней непрерывной эксплуатации объекта в целях поверки и ремонта (например, турбоагрегаты, гидроагрегаты и др.),
- отсутствия возможности замены первичных преобразователей длительное время в условиях эксплуатации,
- необходимости исключения потери метрологической информации в каналах аварийной защиты в процессе эксплуатации
и др.
Оценка метрологических характеристик измерительного канала
При нормировании погрешностей и определении межповерочных интервалов для измерительных каналов необходимо учитывать влияние условий эксплуатации и внешних воздействий, что представляет большую сложность. В зависимости от условий эксплуатации погрешности средства измерения могут резко возрастать [4, 5, 6]. В связи с этим возникает необходимость анализа воздействий влияющих факторов и назначения индивидуального межповерочного интервала для каждого измерительного канала [9].
Так как для измерения параметров машин и механизмов информационно-измерительные системы (или часть их блоков) функционируют в условиях эксплуатации объекта, для учёта влияющих величин (ВВ) и реальных условиях эксплуатации средств измерений (СИ) нормативно введены унифицированные, расширенные и смещённые нормальные условия [6, 7, 8, 9, 10, 11, 12, 13].
На метрологические характеристики СИ влияют: деградация в условиях эксплуатации, внешние воздействия на компоненты СИ, быстропротекающие процессы в компонентах измерительного канала.
Для поддержания работоспособности СИ в настоящее время используются метрологический надзор (поверка и калибровка), связанный с периодическим демонтажом СИ, поверка и калибровка в отсутствие учёта влияющих величин, прерывание процесса эксплуатации объекта для поверки и калибровки СИ.
Основным способом эффективного применения СИ сегодня является увеличение межповерочного интервала и повышение надёжности аппаратных средств, что достигается за счёт применения более надёжных электронных компонентов, введения поправок с учётом срока эксплуатации СИ, резервирования, мажорирования, введения обратных связей и т.д. для электронных блоков и др.
В настоящее время в нашей стране и за рубежом в нормативных документах предъявлены требования к методам и средствам метрологического обеспечения технологических процессов, гибких производственных систем и заводов автоматов [6, 8, 9, 10, 11, 12], которые
- учитывают работу СИ в жёстких условиях эксплуатации при воздействии неконтролируемых влияющих величин,
- позволяют проводить между поверками промежуточный контроль метрологической исправности СИ,
- распространяют метрологическое обеспечение на все СИ, применяемые при контроле и диагностировании,
- разрешают для оценки метрологических характеристик использовать сопоставление близких по точности нескольких параметров,
- узаконивают метрологический диагностический контроль (МКД), но как ограниченную метрологическую операцию, не дающую гарантию обеспечения единства измерений,
- указывают о необходимости разработки встраиваемых систем контроля метрологических характеристик СИ для автоматизированной поверки и калибровки.
Также представлена возможность сопоставления метрологически равноправных по точности параметров для подтверждения основных метрологических характеристик СИ без использования эталонных средств, но в этом случае возможен отрицательный результат, связанный с погрешностями сопоставляемых величин. Используется избыточность измерительной информации, основанной на связях функционально взаимосвязанных параметров, измеряемых различными измерительными каналами. Это особенно актуально для систем, выполняющих большой объём измерений в условиях эксплуатации объекта и требующих постоянного подтверждения установленных метрологических характеристик.
Для фазохронометрических систем (ФХС), построенных по единой методологии для различных циклических машин и механизмов, необходим единый минимально-затратный подход в их метрологическом обеспечении.
При применении ФХС без процедур автоматизированной самодиагностики и самопроверки обойтись невозможно. При реализации алгоритмов самодиагностики проверяется условие о нахождении погрешностей измерительного канала в рамках допустимых границ. При этом необходим общий алгоритм, позволяющий реализовать эту процедуру применительно к ФХС.
Для ФХС, встраиваемых в сложные и дорогостоящие технические системы (турбоагрегаты, гидроагрегаты, ГТД, дизель-генераторы, мощные компрессоры и др.) одним из путей решения этой проблемы является выполнением непрерывной метрологической проверки метрологических характеристик измерительного канала, когда поверочный интервал определяется временем измерений и быстродействием ЭВМ. Данный подход обеспечивает оценку метрологических характеристик практически в реальном времени и при её применении нет необходимости учитывать изменение влияющих величин и выполнять в связи с этим периодически перерасчёт поверочного интервала. То есть оценка годности измерительного канала выполняется по текущим фактическим показателям метрологических характеристик. Реализация этой процедуры осуществляется введением дополнительного измерительного канала. Тогда рабочие каналы выполняют измерения и поочерёдно (или в дублированном варианте) для каждого выполняется расчет метрологических характеристик.
Данная методика реализуется при использовании процедуры многократных измерений, методов планирования измерений при оценке качества измерительной процедуры относительно систематической погрешности и дисперсии с использованием тестового сигнала [14, 15, 16].
Алгоритмы оценки метрологических характеристик измерительного канала рассматриваются в допущении, что результат однократного измерения является случайной величиной и имеет Гауссовский закон распределения.
Результат измерения можно представить в виде
![]() , (1)
, (1)
где t – измеряемая величина – интервал времени, а ![]() - случайная погрешность результата измерения. Случайная величина
- случайная погрешность результата измерения. Случайная величина ![]() должна находиться в поле допуска
должна находиться в поле допуска  с заданной вероятностью.
с заданной вероятностью.
 , (2)
, (2)
где Те – допуск поля допуска, ![]() - малая величина,
- малая величина, ![]() .
.
Величина ![]() может быть записана также в следующем виде
может быть записана также в следующем виде
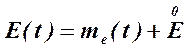 , (3)
, (3)
где ![]() - математическое ожидание случайной погрешности,
- математическое ожидание случайной погрешности, ![]() - центрированная случайная составляющая с дисперсией
- центрированная случайная составляющая с дисперсией ![]() .
.
Условие единства измерений (2) можно записать в виде двух эквивалентных условий [15, 16]
1. ![]() (4)
(4)
2. 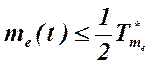 , (5)
, (5)
где ![]()
![]() ,
, ![]() ,
,
![]() - параметр, влияющий на значения ограничений
- параметр, влияющий на значения ограничений ![]() ,
,
![]() ,
, 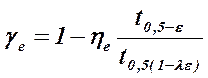 ,
,  ,
,
![]() где:
где: ![]() - квантили функции Лапласа, соответствующие значениям
- квантили функции Лапласа, соответствующие значениям ![]() и .
и .
Выполнение условий (4) и (5) гарантирует выполнение условия (2).
Таким образом, рассматривая задачу оценки метрологического качества работы измерительного канала, следует решить две задачи:
1) Оценить экспериментально условие по дисперсии (4) по результатам измерения величины тестового сигнала t (интервал времени).
2) Оценить экспериментально условие по систематической погрешности (5) по результатам измерения величины тестового сигнала t (интервал времени).
При решении данных задач использовались теоретические положения, рассмотренные в работах [16, 17].
Достоинством предлагаемого подхода является то, что метрологическая оценка работы измерительного канала осуществляется только с помощью проверки выполнения условий (4) и (5) без необходимости проведения подробного анализа составляющих погрешностей измерительных каналов, условий эксплуатации, внешних воздействий и др.
Применением предложенной методики достигается универсальность и гибкость за счет:
- отсутствия необходимости, при выполнении процедуры метрологической проверки работы ФХС на функционирующих циклических машинах и механизмах, экспериментально оценивать постоянно изменяющиеся параметры условий эксплуатации (рис. 1),
- отсутствия необходимости учитывать конкретную реализацию конструкции измерительного канала, его расчётные характеристики. В данном случае измерительный блок рассматривается как «чёрный ящик». Наличие конструктивного несовершенства измерительной системы выявится при проверке выполнения условий (4, 5).

Рис. 1
В случае неудовлетворительного результата проверки выполняется замена измерительного блока, а также анализ влияющих факторов и конструкции.
При выполнении многократных измерений рассматривается схема, когда многократные измерения выполняются измерительным каналом путём подачи тестового сигнала с известным действительным значением tд через фиксированные интервалы времени. Значения интервалов выбираются такими, чтобы обеспечивалось некоррелированность многократных измерений, что выполнимо.
При равноточных некоррелированных измерениях оценка измеряемой величины (периода следования тестового сигнала) ![]() имеет вид
имеет вид
 , (6)
, (6)
где
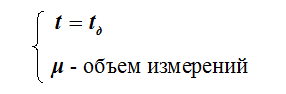
Числовые характеристики этой оценки имеют вид
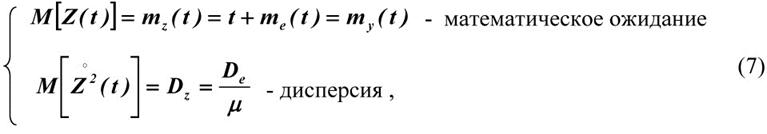
где ![]() - дисперсия результата однократного измерения.
- дисперсия результата однократного измерения.
Исходными данными для реализации плана измерений являются следующие характеристики фазохронометрической системы: абсолютная погрешность однократного измерения интервалов времени ФХС
Те = ±1·10-7с.;
абсолютная погрешность тестового сигнала ±1·10-9с, что позволяет принять ![]() . При этом входной тестовый сигнал принимается постоянной величиной, так как измерительный канал не чувствителен к вариациям его периода.
. При этом входной тестовый сигнал принимается постоянной величиной, так как измерительный канал не чувствителен к вариациям его периода.
При построении алгоритмов введем следующие условия их применимости: однократное измерение есть гауссовская случайная величина с систематической погрешностью, удовлетворяющей заданным ограничениям.
Структура результата однократного измерения
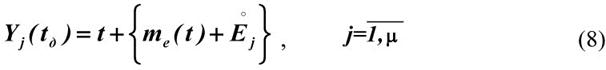
где ![]() - центрированная случайная составляющая с дисперсией
- центрированная случайная составляющая с дисперсией ![]()
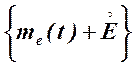 - погрешность, вносимая средством измерения.
- погрешность, вносимая средством измерения.
Формирование плана измерения при оценке условия по дисперсии
Измерительная задача, связанная с проверкой условия ![]() , сводится к схеме альтернативных гипотез
, сводится к схеме альтернативных гипотез
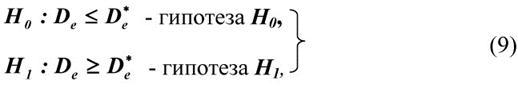
Апостериорное решение о том, какая из указанных гипотез имеет место, принимается на основе решающей функции следующего вида

где u0 –constи параметр решающей функции.
Параметрами плана, которые нужно определить до реализации эксперимента являются: ![]() - объём многократных измерений, u0 – параметр решающей функции.
- объём многократных измерений, u0 – параметр решающей функции.
В обеспечении плана эксперимента помимо указанных параметров указывается ещё и измеряемая величина тестового сигнала t.
Таким образом, структура плана эксперимента имеет следующий вид ![]() , где
, где ![]() - план измерения для многократных измерений с использованием тестового сигнала.
- план измерения для многократных измерений с использованием тестового сигнала.
При использовании решающей функции (10) важным моментом является выбор аргумента и, очевидно, что в качестве аргумента U при проверке гипотез (1) следует выбрать экспериментальную оценку дисперсии, которую можно получить только на основе многократных измерений
![]()
Оценка дисперсии как случайная величина при указанных выше допущениях имеет следующий вид
 , (11)
, (11)
где
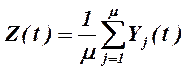 . (12)
. (12)
 - случайная величина, имеющая центральное
- случайная величина, имеющая центральное ![]() - распределение с
- распределение с ![]() степени свободы.
степени свободы.
После подстановки в правой части равенства получим случайное событие состоящее в том, что принимается гипотеза Н0. Вероятность случайного
события определяется выражением, зависящим от аргумента De оперативной характеристикой решающей функции, которая является оперативной характеристикой решающей функции.

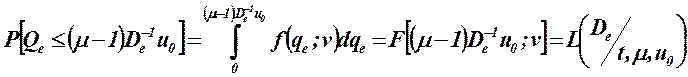 , (14)
, (14)
Значения оперативной характеристики определяют вероятность принятия гипотезы Н0. На интервале гипотезы Н0: ![]() это вероятность правильной оценки гипотезы Н0, а дополнение вероятности до единицы определяет вероятность ошибочно оценить эту гипотезу как гипотезу Н1.
это вероятность правильной оценки гипотезы Н0, а дополнение вероятности до единицы определяет вероятность ошибочно оценить эту гипотезу как гипотезу Н1.
Это вероятность ошибки 1-го рода
 . (15)
. (15)
На интервале гипотезы Н1функция  определяет вероятность ошибочно оценить гипотезу Н1, как гипотезу Н0. Это вероятность появления ошибки 2-го рода
определяет вероятность ошибочно оценить гипотезу Н1, как гипотезу Н0. Это вероятность появления ошибки 2-го рода
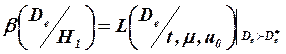 . (16)
. (16)
При ![]() имеет место следующее равенство
имеет место следующее равенство
 .
.![]() (17)
(17)
Данная зависимость свидетельствует о том, что при ![]() и малой окрестности точки
и малой окрестности точки ![]() невозможно обеспечить малые значения вероятностей ошибок 1-го и 2-го рода. Вследствие этого используют интервальную оценку.
невозможно обеспечить малые значения вероятностей ошибок 1-го и 2-го рода. Вследствие этого используют интервальную оценку.
Определим границы этой малой окрестности
![]() , <1 , (18)
, <1 , (18)
![]() ,
, ![]() >0 .
>0 .
Для гипотез ![]() и
и ![]() введём следующие ограничения на вероятность ошибок 1-го и 2-го рода
введём следующие ограничения на вероятность ошибок 1-го и 2-го рода
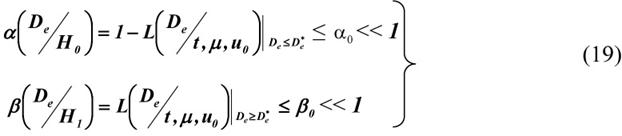
или

где ![]() - наиболее предпочтительная часть гипотезы Н0,
- наиболее предпочтительная часть гипотезы Н0,
![]() - наименее предпочтительная часть гипотезы Н1.
- наименее предпочтительная часть гипотезы Н1.
Для определения параметров ![]() и U0в отношениях (20) оставим только знаки равенства и получим систему уравнений с двумя неизвестными
и U0в отношениях (20) оставим только знаки равенства и получим систему уравнений с двумя неизвестными ![]() и
и ![]()
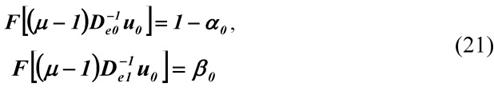
Или переходим к уравнениям для квантилей
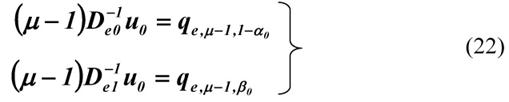
где ![]() и
и ![]() - квантили функции центрального
- квантили функции центрального ![]() - распределения с
- распределения с ![]() степени свободы.
степени свободы.
Решения системы уравнений имеют следующий вид
![]() , (23)
, (23)
где ![]()
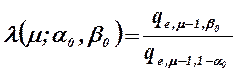 - монотонно возрастающая функция, удовлетворяющая условию
- монотонно возрастающая функция, удовлетворяющая условию ![]() .
.
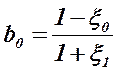 < 1 (24)
< 1 (24)
 (25)
(25)
План эксперимента ![]() является оптимальным, так как обеспечивает выполнение заданных ограничений на вероятность ошибок 1-го и 2-го рода (19) при минимальном объёме многократных измерений.
является оптимальным, так как обеспечивает выполнение заданных ограничений на вероятность ошибок 1-го и 2-го рода (19) при минимальном объёме многократных измерений.
Оперативная характеристика является монотонно убывающей функцией аргумента ![]() . Следствием этого является функция
. Следствием этого является функция  , которая монотонно возрастает, а
, которая монотонно возрастает, а 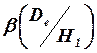 - монотонно убывает. Следовательно, в граничных точках
- монотонно убывает. Следовательно, в граничных точках ![]() и
и ![]() вероятности ошибок достигают максимального значения ограниченного пределами
вероятности ошибок достигают максимального значения ограниченного пределами ![]() << 1 и поэтому на интервалах гипотез
<< 1 и поэтому на интервалах гипотез ![]() и
и ![]() условия (9) всегда выполняются.
условия (9) всегда выполняются.
Заключение
Рассмотренный подход позволяет реализовать
- план эксперимента  оценки метрологических характеристик измерительного канала, функционирующего в условиях эксплуатации объекта,
оценки метрологических характеристик измерительного канала, функционирующего в условиях эксплуатации объекта,
- план эксперимента при оценке систематической погрешности измерительного канала по условию

- план 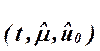 при оценке ограничения на случайную погрешность.
при оценке ограничения на случайную погрешность.
Список литературы
1. Пронякин В.И. Проблемы диагностики циклических машин и механизмов // Измерительная техника. 2008. № 10. С. 9-13.
2. Киселёв М.И., Зройчиков Н.А., Пронякин В.И., Чивилев Я.В. Прецизионное исследование работы турбоагрегата оптико-электронными средствами // Теплоэнергетика. 2006. № 11. С. 10-13.
3. Киселёв М.И., Пронякин В.И. Фазовый метод исследования циклических машин и механизмов на основе хронометрического подхода // Измерительная техника. 2001. № 9. С. 15-18.
4. Колтик Е.Д., Тайманов Р.Е., Кочугуров В.В., Сапожникова К.В., Дружинин И.И. Методы определения метрологических параметров электрофизических преобразователей, встроенных в агрегаты // Измерительная техника. 1987. № 10. С. 6-8.
5. Цейтлин Я.М. Нормальные условия измерений в машиностроении. Л.: Машиностроение, 1982. 224 с.
6. МИ 1888-88. Методические указания. ГСИ. Нормальные условия измерений в гибких производственных системах. М.: Изд-во стандартов, 1989. 14 с.
7. Тарбеев Ю.В., Иванов В.Н., Новицкий П.В. Научно-технические перспективы обеспечения метрологической надёжности средств измерений // Измерительная техника. 1982. № 5. С. 17-19.
8. МИ 2440-97. ГСИ. Методы экспериментального определения и контроля характеристик погрешности измерительных каналов измерительных систем и измерительных комплексов. М.: ВНИИМС, 1997. 13 с.
9. МИ 2267-2000. ГСИ. Обеспечение эффективности измерений при управлении технологическим процессом. Метрологическая экспертиза технической документации. М.: ВНИИМС, 2000. 26 с.
10. МИ 2232-2000. ГСИ. Обеспечение эффективности измерений при управлении технологическими процессами. Оценивание погрешности измерений при ограниченной исходной информации. М.: ВНИИМС, 2000. 10 с.
11. МИ 2233-2000. ГСИ. Обеспечение эффективности измерений при управлении технологическими процессами. Основные положения. М.: ВНИИМС, 2000. 15 с.
12. ГОСТ Р 8.565-96. Государственная система обеспечения единства измерений. Метрологическое обеспечение эксплуатации атомных станций. Основные положения. М.: Госстандарт России, 1996. 11 с.
13. Проблемы машиностроения: точность, трение и износ, надёжность, перспективные технологии / под ред. В.П. Булатова. СПб.: Наука, 2005.740 с.
14. Шеффе Г. Дисперсионный анализ : пер. с англ. М.: Физматгиз, 1963. 370 с.
15. Назаров Н.Г. Измерения: планирование и обработка результатов. М.: Издательство стандартов, 2000. 304 с.
16. Монтгомери Д.К. Планирование эксперимента и анализ данных : сокр. пер. с англ. В. А. Коптяева. Л.: Судостроение, 1980. 383 с.
17. Климачев Д.В. Методика определения оптимальных ограничений на вероятности ошибок 1-го и 2-го рода при контроле партии однородных изделий: дис. … канд. техн. наук. М., 2003. 123 с.
Публикации с ключевыми словами: измерение, диагностика, интервалы времени, фазохронометрический метод, фазохронометрическая система, измерительный канал
Публикации со словами: измерение, диагностика, интервалы времени, фазохронометрический метод, фазохронометрическая система, измерительный канал
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



