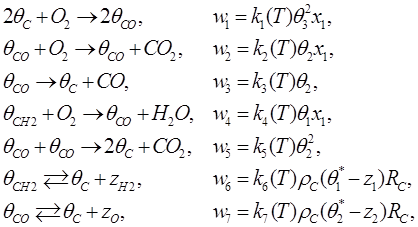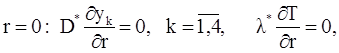научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2012
DOI: 10.7463/1212.0507309
УДК 004.942
Институт нефтехимии и катализа РАН
avbalaev@gmail.com
irekmars@mail.ru
leniza.sayfullina@gmail.com
Введение
Каталитические процессы широко распространены в химической, нефтехимической и нефтеперерабатывающей промышленности. В ходе эксплуатации оборудования, использующего таких процессов, наблюдается ухудшение режимных показателей, основной причиной которого является отложение кокса на активной поверхности катализатора. Для восстановления активности катализатора, как правило, используют окислительную регенерацию [1].
От успешности процесса регенерации зависит уровень активности и стабильности регенерационного катализатора, поэтому имеется реальная потребность в доступном проблемно-ориентированном программном обеспечении, обеспечивающем математическое и компьютерное моделирование данного процесса. Велика также потребность в организации совместной работы коллектива исследователей, инженеров и заказчиков, в накоплении и передаче знаний, информационной поддержке образовательного процесса. Такие возможности сочетают в себе интерактивные приложения, работающие в сети Интернет и получившие общее название Web-приложений. Современные Web-приложения – это сложные программные комплексы, разработка и поддержание которых становится непростой задачей [2].
Результаты детальных исследований зависимости основных характеристик процесса (глубины и времени выжига кокса, разогревов на зерне и в слое катализатора) от значений управляющих параметров процесса (температуры и скорости подачи газового потока, начальной концентрации кислорода) приведены в работах [1, 3]. Однако использовавшееся авторами математическое и программное обеспечение в настоящее время устарело. Примеры применения современных Web-приложений для анализа процесса окислительной регенерации в научной литературе отсутствуют.
Целью данного исследования является разработка комплекса Web-программ для моделирования процессов окислительной регенерации закоксованных катализаторов в виде виртуальной лаборатории.
Для достижения поставленной цели необходимо решить следующие задачи:
– разработать математическое описание процесса окислительной регенерации катализаторов в виде систем алгебраических и дифференциальных уравнений, выражающих основные законы сохранения;
– разработать программный комплекс для моделирования, а также построить структурно-функциональную модель виртуальной лаборатории как среды для размещения разработанных приложений;
– на основе реализованных моделей провести численные исследования изменения основных характеристик процесса регенерации от вариации значений управляющих параметров процесса.
1. Математическое описание процесса
Стратегия моделирования заключается в последовательном исследовании и анализе основных закономерностей регенерации на моделях различных уровней – на кинетическом уровне, уровнях зерна и слоя катализатора, а также на уровне контактного аппарата в целом.
Первый уровень многоступенчатой модели любого реактора – кинетическая модель. Кинетическая модель представляет собой совокупность моделей элементарных стадий, реакций и уравнений, характеризующих зависимость скорости химического превращения от параметров реакции ‑ давления, температуры, концентраций реагентов и др. Такие зависимости определяются на основе экспериментальных данных. Кинетическая модель является первым уровнем модели любого реактора и базисом для его математических моделей. Достаточно надёжная кинетическая модель выжига кокса, позволяющая с необходимой точностью рассчитывать не только скорость удаления кокса, но и состав газовой фазы в регенераторе, представлена в работе [3].
Схему превращений, а также соответствующие ей кинетические уравнения скоростей стадий, записываем в виде
| (1) |
где ![]() – скорости отдельных стадий, измеренные в моль/(м2∙с) для
– скорости отдельных стадий, измеренные в моль/(м2∙с) для ![]() и в г/(м2∙с) для
и в г/(м2∙с) для ![]() ; ki(T) – константы скоростей стадий, зависящие от температуры T по уравнению Аррениуса и измеренные в моль/(м2∙с) для k1-k5 и в м2/с для k6-k7; x1 – концентрация кислорода в газовой фазе, мольные доли; zj – концентрация водорода (z1=zH2) и кислорода (z2=zO) в объеме коксовых отложений, г/г; θk – степени покрытия поверхности кокса различными углеродными комплексами (θ1= θCH2 – водород-углеродный комплекс, θ2= θCO – кислород-углеродный комплекс, θ3= θC – свободная углеродная поверхность); θl* - количества адсорбированных коксом водорода и кислорода (l=1 и l=2 соответственно), равновесных относительно текущего состояния поверхности коксовых отложений, г/г; ρС – плотность кокса, г/м3; RC – средний радиус коксовых гранул, м.
; ki(T) – константы скоростей стадий, зависящие от температуры T по уравнению Аррениуса и измеренные в моль/(м2∙с) для k1-k5 и в м2/с для k6-k7; x1 – концентрация кислорода в газовой фазе, мольные доли; zj – концентрация водорода (z1=zH2) и кислорода (z2=zO) в объеме коксовых отложений, г/г; θk – степени покрытия поверхности кокса различными углеродными комплексами (θ1= θCH2 – водород-углеродный комплекс, θ2= θCO – кислород-углеродный комплекс, θ3= θC – свободная углеродная поверхность); θl* - количества адсорбированных коксом водорода и кислорода (l=1 и l=2 соответственно), равновесных относительно текущего состояния поверхности коксовых отложений, г/г; ρС – плотность кокса, г/м3; RC – средний радиус коксовых гранул, м.
В практике математического моделирования процесса окислительной регенерации выявлению закономерностей выжига кокса на зерне катализатора уделяется серьёзное внимание. Основной вопрос, интересующий исследователей, – какие перегревы возможны при регенерации зёрен катализатора в зависимости от выбора начальных условий ‑ массы отложившегося кокса, температуры, концентрации кислорода в газе и размера зёрен.
При построении модели сделаны допущения: 1) зерно катализатора сферическое, его размер и структура пор не изменяются в ходе процесса; 2) теплофизические параметры, коэффициенты тепломассопереноса и обмена и энергии активации инвариантны относительно изменения температуры; 3) массой газа в порах по сравнению с массой зерна катализатора можно пренебречь; 4) отложения кокса имеют вид гранул, число которых в ходе регенерации не меняется.
Тогда уравнения материального и теплового балансов с учётом переносов за счёт диффузии, теплопроводности и стефановским потоком имеют вид [1]
| (2) |
| (3) |
где начальные условия (
|
(4) |
а граничные условия – выражения
|
(5) |
r=RЗ: | (6) |
Расчет процессов окисления кокса проводился в реакторе с неподвижным слоем катализатора и с движущимся слоем контактного материала. Математическую модель в неподвижном слое катализатора можно представить уравнениями материального по кислороду и по коксу и уравнением теплового балансов [4]:
| (7) |
 начальные и граничные условия имеют, соответственно, вид
начальные и граничные условия имеют, соответственно, вид
| (8) |
| (9) |
Представленная математическая модель реактора с неподвижным слоем катализатора является общей математической моделью и может быть использована для исследования и расчета ряда регенерационных устройств:
Для изотермического реактора имеем место равенство ∂T/∂l=0, и если рассматривать режим с постоянной в ходе всей регенерации температурой ∂T/∂τ=0, то последнее уравнение системы (7) переходит в независимое условие постоянства температуры, а процесс описывается двумя первыми уравнениями.
Использование общей модели (7) позволяет производить расчеты и адиабатических реакторов. Теплопередачи через стенку регенератора не происходит, поэтому тепловое уравнение в системе также упрощается:
Формулы (7) – (9) для слоя катализатора взяты из работы [4]. Однако автор характеризует процесс выжигания коксовых отложений единой скоростью W. На самом деле различные компоненты «кокса» выжигаются с разными скоростями, поэтому использовалась описанная выше кинетическая модель (1).
Решение системы уравнений (2) – (6) проводится методом матричной прогонки с использованием вычислительного алгоритма, разработанного в [5].
Что касается математического описания процессов регенерации в слое катализатора, то система уравнений (7)-(9) заменялась приближенными уравнениями в конечных разностях, согласно алгоритму, изложенному в [4] за единственным исключением: вместо единой скорости выжигания кокса использовалась сумма скоростей кинетической модели (1).
2. Архитектура приложения
Для реализации данных математических моделей была разработана виртуальная лаборатория, которая представляет собой Web-приложением. Web-приложение написано на языке программирования Java.
Web–приложение на Java представляет собой совокупность таких компонентов как Java–сервлеты, Java Server Page, драйверы для работы с БД, дескриптор доставки, статические компоненты (HTML-страницы, каскадные таблицы стилей CSS, изображения), прочие ресурсы.
Приложение реализует паттерн проектирования Model-view-controller (Модель-вид-контроллер). Данная аббревиатура отражает тот факт, что приложение представляет собой три взаимодействующих части:
Модель отвечает за управление данными, она сохраняет и извлекает сущности из БД и содержит логику, реализованную в приложении.
Представление несет ответственность за отображение данных, которые дает контроллер. В данном приложении Web-приложении представление реализуется в виде страницы JSP.
Контроллер связывает модель и представление. В роли контроллера в данном приложении выступает сервлет. Он получает запрос от клиента, анализирует его параметры и обращается к модели для выполнения операций над данными запроса. От модели поступают уже скомпонованные объекты. Затем они перенаправляются в представление, генерируемое сервлетом. Представление отображает конечную информацию.
Таким образом, в данном паттерне выделены отдельные функциональные компоненты, следовательно, изменения, вносимые в один из компонентов, оказывают минимальное воздействие на другие компоненты, что позволяет создавать гибкие и масштабируемые приложения.
3. Вычислительный эксперимент в Web-лаборатории
3.1. Описание программного комплекса.
Разработано Web-приложение в виде виртуальной лаборатории, направленной на решение широкого круга задач естественнонаучной направленности.
Для адаптации в Web-лаборатории уже написанных программ на С++ была применёна технология JavaNativeInterface (JNI) – стандартный механизм для запуска кода, под управлением виртуальной машиныJava(JVM), который написан на языках С/С++, и скомпонован в виде динамических библиотек.
На сегодняшний день виртуальная лаборатория состоит из одного раздела «Окислительная регенерация», представляющего собой отдельную Web-страницу с удобным интерфейсом, и базы данных кинетических исследований, разработанную в Институте нефтехимии и катализа РАН.
Интерфейс включает в себя описательный блок, который несет в себе информацию о названии исследуемой модели, системах уравнений, характеризующих данную модель.
Имеются все необходимые элементы управления для исследования: поля для ввода значений начальных условий и параметров, определяющих поведение модели; переключатели, определяющие вариант вывода результатов на экран для сравнения результатов; кнопка для запуска расчетов.
С помощью блок вывода результатов расчета выполнен вычислительный эксперимент и получены результаты в виде графических зависимостей.
3.2. Численный анализ процесса регенерации катализаторов
Вопрос о максимальных разогревах на зерне катализатора ставят все исследователи [5], занимающиеся моделированием процесса на уровне зерна катализатора. Интерес к этой проблеме понятен: перегревы катализатора вызывают его растрескивание, снижающие механическую прочность и активность, что приводит к увеличению расхода катализатора.
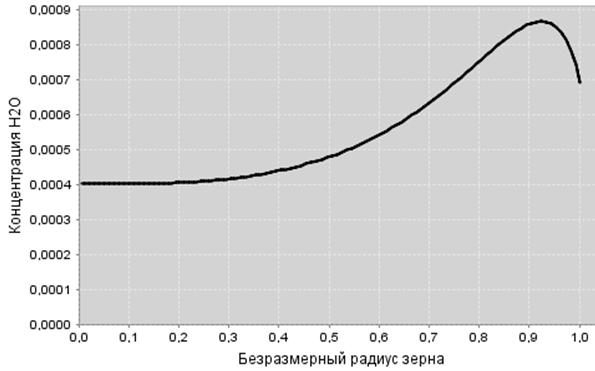
Для оценки разогрева зерна катализатора с помощью математического описания (2) – (3) с начальными и граничными условиями (4) – (6) выполнены расчеты, результаты которых представлены на рисунке 1. В качестве базисного выбран следующий набор параметров: qc0 = 5 % (мас.), x10 = 2,0 % (об.), T0 = 500 °C, dЗ = 5 мм.

а)
б)

в)

г)
Рисунок 1 ‑ Концентрации компонентов в порах зерна катализатора по радиусу зерна:
а) O2; б) H2O; в) CO2; г) CO
Характер изменения распределения температуры по радиусу зерна катализатора приведен на рисунке 2; кривые соответствуют следующим входным температурам: 400 °С, 420 °С, 440 °С, 460 °С, 480 °С, 500 °С.

Рисунок 2 ‑ Распределение температуры по радиусу зерна при различных входных температурах кислородсодержащего газа
Проиллюстрируем применение соотношений (7) – (9) для расчета регенерации слоя алюмосиликатного катализатора воздухом. Расчеты проводились для начального содержания кокса 5,3 %, содержания кислорода 23 %, плотности газа 1,2∙10-3 г/см3, пористости 0,42, линейной скорости подачи газа V0/S = 10 см/мин, N1 = 0,505∙10-3 г/см3 и N2 = 0,0122 г/(см3∙мин). Результаты расчетов представлены на рисунках 3-4.
Рисунок 3 иллюстрирует уменьшение во времени количества кокса, остающегося на катализаторе и отнесенного к его первоначальному количеству в изотермическом реакторе, рисунок 4 – изменение содержания кислорода.
При высоких температурах концентрация кислорода резко падает в первых по ходу газа слоях катализатора. Соответственно выжигание кокса происходит интенсивнее также в передних слоях и наблюдается близкое к послойному выгорание кокса.

Рисунок 3 ‑ Распределение относительного содержания кокса на катализаторе по длине регенерируемого слоя во времени

Рисунок 4 ‑ Изменение относительной концентрации кислорода в кислородсодержащем газе в зависимости от относительной длины слоя во времени
С увеличением коксоотложения на катализаторе концентрация кислорода по длине слоя падает быстрее, а время, требуемое для полной регенерации катализатора, возрастает.
Заключение
В результате исследовательской работы был разработан комплекс программ для математического моделирования процессов окислительной регенерации катализаторов в виде виртуальной лаборатории, предоставляющей доступ удаленному пользователю к программному обеспечению. Исследованы и реализованы методы построения Web-приложений с использованием технологии Java. Произведен вычислительный эксперимент в Web-лаборатории, в результате которого найдены зависимости характеристик процесса регенерации от значений основных параметров процесса на следующих уровнях:
- на единичном пористом зерне катализатора;
- в неподвижном слое катализатора (в двух тепловых режимах – адиабатическом и изотермическом).
Разработанный комплекс программ, представляющий собой виртуальную лабораторию, обладает следующими свойствами и характеристиками:
- способен работать как в локальной, так и в глобальной сети в режиме on-line;
- не требует установки никакого дополнительного программного обеспечения;
- обладает графическим интерактивным интерфейсом, позволяющим проводить вычислительные эксперименты.
Адрес лаборатории в Интернете 31.131.18.243:8080/mathmodeling.
Список литературы
1. Масагутов Р.М., Морозов Б.Ф., Кутепов Б.И. Регенерация катализаторов в нефтехимии и нефтепереработке. М.: Химия, 1987. 143 с.
2. Носов В.П. Исследование и разработка методов построения и кэширования веб-приложений: автореф. дисс. … канд. техн. наук. Москва, 2009. 21 с.
3. Балаев А.В., Дробышевич В.И., Губайдуллин И.М., Масагутов Р.М. Исследование волновых процессов в регенераторах с неподвижным слоем катализатора // Распространение тепловых волн в гетерогенных средах : сб. науч. тр. / АН СССР, Сиб. отд-ние, Ин-т катализа ; Отв. ред. Ю. Ш. Матрос. Новосибирск: Наука, 1988. С. 233-246.
4. Жоров Ю.М. Моделирование физико-химических процессов нефтепереработки и нефтехимии. М.: Химия, 1978. 376 с.
5. Губайдуллин И.М. Математическое моделирование динамических режимов окислительной регенерации катализаторов в аппаратах с неподвижным слоем: дис. … канд. физ.-мат. наук / Институт Нефтехимии и катализа АН РБ. Уфа, 1996. 109 с.
Публикации с ключевыми словами: окислительная регенерация закоксованных катализаторов, виртуальная лаборатория, вычислительный эксперимент
Публикации со словами: окислительная регенерация закоксованных катализаторов, виртуальная лаборатория, вычислительный эксперимент
Смотри также:
- Теплопроводность композита с нетеплопроводными шаровыми включениями
- Образование упорядоченных пространственно-временных структур поля в круглом сверхразмерном резонаторе, возбуждаемом широкополосными ансамблями циклотронных осцилляторов
- Математическое моделирование рабочего процесса в гидроприводе на основе регулируемых аксиально-поршневых гидромашин
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||