научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#1 январь 2005
Д. И. Кардаш, А. В. Кудрявцев, канд. техн. наук,
А. И. Фрид, канд. техн. наук, Уфимский государственный авиационный технический университет
Об одном методе тестового диагностирования сложных систем
В статье предлагается новый подход к решению задачи тестового диагностирования сложных систем. Приведен разработанный алгоритм диагностирования системы при проведении тестовых испытаний. Описание метода проиллюстрировано примером.
Ставится задача построения алгоритма диагностирования сложных систем. Использование для систем высокой сложности метода тестирования с применением таблицы функций неисправностей [1] проблематично в силу большой трудоемкости построения этих таблиц. Существует метод тестирования, использующий Д-алгоритм, впервые предложенный в работе [2]. Это метод активизации многомерных путей, использующий математический аппарат кубических комплексов Рота [3]. Он применим для комбинационных схем, задающихся с помощью таблиц истинности. Кроме того, при осуществлении Д-алгоритма Рота происходит построение таблиц неисправностей [4], что при большой сложности диагностируемой системы практически неосуществимо. Подобным недостатком обладает и метод построения дерева отказов.
Само по себе дерево отказов является удобной моделью не только для тестового, но и для функционального диагностирования. На его основе можно легко построить тестирующий автомат (например, при микропрограммной генерации тестов [5]), для которого разработано достаточное количество алгоритмов функционирования [6]. Процедура построения дерева отказов для сложных систем достаточно трудоемка.
Синтез тестирующего автомата без построения дерева отказов предполагает определение словаря неисправностей (примером может служить построение корректирующих автоматов для исправления ошибок в логических схемах, описанное в [7]), что также является трудоемким процессом.
Применяемая в [8] диагностическая модель использует полюсные графы, описываемые матрицей W (матрицей характеристик компонентов любой природы). Сущность метода заключается в решении уравнения Wx = Q, где x — вектор реакций исследуемого объекта, a Q — задающие воздействия. При решении этого уравнения определяются свойства элементов и их групп, участвующих в формировании той или иной реакции объекта, что позволяет оценить систему по тому или иному критерию (например, по надежности). При этом наборы x и Q предлагается определять экспериментально, что неприменимо для сложных систем в силу значительных затрат как на проектирование тестов, так и на время их функционирования (даже в случае, когда время тестирования не ограничено временными рамками проекта, расходуются ресурсы диагностируемого объекта).
Другим методом диагностирования объектов, описываемых с помощью графа, является метод, использующий алгоритм МИПГ (максимально-изоморфного пересечения графов) [9]. Использование в качестве модели системы графа облегчает ее алгоритмическую обработку. Несмотря на алгоритмическую простоту такого метода (реализация алгоритма языками Паскаль и ПЛ/1 приведены в [9]), в конечном итоге, он сводится к методу дублирования и сравнения [10], при котором предполагается наличие эталонной схемы, т. е. "работоспособного" графа. Этот метод успешно применяется при автоматизации контроля в САПР БИС; в случае же, если диагностируемая система рассматривается не только с точки зрения топологии, метод малоприменим. Но даже при решении задач диагностирования БИС не удается обойтись тестированием только топологии [11].
В работе [12] рассматривается подход, который использовался на практике при надежностном анализе архитектур устройств ввода информационно-управляющих комплексов бортовых вычислительных систем. В нем применена операция логического умножения матриц. С помощью этой операции, проведенной над матрицей определенное число раз (задается количеством узлов графа, описывающего архитектуру устройства; граф чисто последовательный — архитектуры с обратными связями не рассматривались), определяются все возможные пути прохождения информации. Для нахождения момента окончания поиска путей требуется контролировать число умножений матрицы, что создает определенные неудобства при практическом применении метода.
Любая сложная система (процесс) может быть представлена структурой, которая должна содержать следующие элементы:
· операционные блоки (состоящие из определенной последовательности действий), имеющие несколько входов и один выход;
· переходы, соединяющие все составные части структурной схемы процесса;
· блоки ветвления, которые могут иметь несколько входов и несколько выходов, причем процесс может идти только по одному из выходов в соответствии с поставленным в блоке условием;
· блоки распараллеливания процесса, имеющие так же, как и блоки ветвления, несколько входов и несколько выходов (не менее двух), но в этом случае процесс может идти по всем выходным переходам одновременно;
· блоки концентрации переходов, имеющие несколько входов (не менее двух) и один выход (по входным переходам процесс протекает одновременно).
Каждому элементу структуры соответствует некоторое множество тех или иных (в соответствии с природой процесса) параметров. Обозначим их прописными буквами латинского алфавита с различными номерами: А — операционный блок; В — блок ветвления; С — блок распараллеливания; D — концентратор. Например, множества, соответствующие определенным блокам, могут иметь следующий состав: Ai = {вероятность безотказной работы; время выполнения; используемые вычислительные ресурсы и др.}, Bi = {правило перехода; вероятность правильного перехода по первому пути; вероятность правильного перехода по второму пути} и т. п. Система целиком будет описываться структурой и множеством U, элементами которого будут все множества Ai, Bi, Ci, Di.
Для решения поставленной задачи необходимо формализовать метод определения подмножества множества U, что позволило бы при использовании определенного алгоритма обработки данных искомого подмножества оптимальным образом провести тестирование процесса. Решение данной задачи позволит осуществить тестирование сложных интегрированных систем, для которых необходимо определить правильность совместного функционирования всех компонентов. Успешное завершение отладки и испытаний частей системы не является гарантией работоспособности системы в целом. Это объясняется сложностью обеспечения полноты проверки отдельных частей и их связей и приводит к необходимости комплексной проверки (подробнее об этой проблеме применительно к информационно-вычислительным комплексам см. в [13]).
Гипотетическую структуру системы можно изобразить, используя следующие условные графические изображения: прямоугольник — операционный блок; ромб — блок ветвления; треугольник — блок распараллеливания и концентрации процесса (в случае распараллеливания входные переходы направлены на вершину треугольника, а выходные — из его ребра, для концентратора — наоборот) и стрелка — переход.
♦ На первом этапе решения задачи предстоит осуществить свертку структуры и ее преобразование в граф, способ построения которого описан в [8].
На рис. 1 представлено графическое отображение структуры некоторого процесса, составленное по описанным правилам. На первом шаге преобразования рассмотрим группы элементов, выполняющихся в параллельных путях. Если эта группа не имеет в своем составе элементов распараллеливания, то всю подобную группу можно представить как целую подсистему (формально соответствующую операционному блоку). Группа элементов, обозначенная на рис. 1 областью "а", свертывается до операционного блока и анализируется уже самостоятельно по приведенному ниже алгоритму. На втором шаге происходит преобразование распараллеленных участков процесса к виду операционного блока (область "б" на рис. 1). Определение параметров этого блока ведется исходя из логики распараллеливания и в данной работе не рассматривается.

Рис. 1. Структура процесса
Полученное после подобных преобразований графическое отображение структуры примет вид, представленный на рис. 2. Множество А получается в результате этих преобразований свертываемых областей структуры процесса.
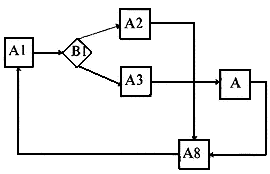
Рис. 2. Структура процесса после преобразования
На третьем шаге осуществляется процесс перераспределения элементов множеств параметров блоков между собой с той целью, чтобы все параметры были сгруппированы в множествах, приписываемых операционным блокам, т. е. чтобы множества Bi, Ci, Di оказались пустыми. Переходам между блоками тоже могут соответствовать множества параметров. С ними проводятся точно такие же преобразования. Например, в множество А1 добавляется элемент "правило перехода" из множества В1,а в А2 и АЗ — вероятности правильных переходов по обоим направлениям из множества В1, которое и остается пустым. Множество U на третьем шаге будет включать в себя только элементы Ai (все остальные его подмножества будут пустыми).
В полученной свернутой структуре (рис. 2) отсутствуют параллельные процессы, что позволяет перейти к следующему этапу формализации.
♦ На втором этапе решения задачи из полученной свернутой структурной схемы построим граф, состоящий из следующих элементов:
· V — пронумерованное множество узлов графа мощности N (они соответствуют блокам ветвления и переходам);
· X — множество вершин графа (они соответствуют операционным блокам);
· L — множество ориентированных дуг графа, соединяющих его вершины и узлы.
Введем следующие принципы построения данного типа графов:
а) каждая вершина имеет только одну входящую и одну выходящую дуги;
б) дуга, выходящая из вершины, обязательно ведет в узел и наоборот.
В используемом примере в графе присутствуют четыре узла и пять вершин. Его вид приведен на рис. 3. Для более точного описания функционирования процесса определим понятие "единичная вершина". Единичная вершина — это элемент графа, соответствующий в структуре процесса операционному блоку, не содержащему никаких действий, — эквиваленту ожидания разрешения перехода.

Рис. 3. Представление структуры процесса графом
Для структуры процесса этот блок является фиктивным и на графическом отображении структуры системы не приводится. Своими физическими параметрами (временем ожидания, условием разрешения перехода и др.) он отнесен к одному или нескольким операционным блокам. Но в построенном графе каждый узел может быть представлен в виде фрагмента, представленного на рис. 4. С точки зрения тестирования системы единичные элементы интереса не представляют, поэтому нет необходимости изображать их на графе.
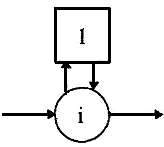
Рис. 4. Введение единичного элемента
Поставим в соответствие множеству Ai событие ai такое, что выполнение процесса инициирует выполнение элемента структуры, характеризуемого Ai. Назовем путем между двумя узлами с номерами i и j подмножество рi, j множества Х такое, что все его элементы лежат на ориентированном пути между этими узлами. Расстоянием между узлами или длиной пути назовем мощность множества pi,j. Отметим, что пути могут проходить через узел только один раз. Это условие необходимо, чтобы избежать бесконечного наращивания пути за счет ориентированных циклов. Два узла будем называть "смежными", если между ними существует путь единичной длины.
Для формального описания этого графа построим квадратную матрицу М размерностью N х N по следующему правилу: элементами матрицы являются множества Pi,j (в случае, если не существует путей, ведущих из i-го узла в i-й узел, то множество пусто), при этом учитываем и единичные вершины (i — номер строки матрицы, j — номер ее столбца). Множество Рi,j - у будет включать в себя элементы, представленные всеми возможными непустыми множествами pij и в случае i = j — путем единичного элемента, символически отображаемого как "1".
Определим операцию поэлементного пересечения матриц. Для двух квадратных матриц D и В одинаковой размерности N (их элементы соответственно — dj,j и bj,j) результатом операции является матрица С, элементы которой определятся в
виде:
![]() (1)
(1)
Усечем полученные множества сi,j по следующим правилам:
— исключаются все, кроме одного, одинаковые элементы;
— исключаются те элементы d, для которых
существует такой элемент b, что ![]() .
.
Назовем степенью матрицы (в случае, если эта операция производится над
одним операндом) количество проведенных поэлементных пересечений над исходной
матрицей. Будем обозначать матрицу, пересеченную сама с собой n раз, — Мn.
Применяя эту операцию к матрице М, можем получить ее "квадрат"
![]() ,
"куб"
,
"куб" ![]() и т.д.
и т.д.
Для рассматриваемого случая матрица будет иметь вид:

В матрице М расстояние между двумя узлами (если этот путь
существует) равно единице. Получим матрицу М2, элемент сi,j
которой будет представлять набор пересечений множеств событий прохождения
вершин, принадлежащих всем путям единичной длины, выходящим из узла i, и множеств событий прохождения вершин, принадлежащих
путям, входящим в узел j. Для путей, не
содержащих узла, в который входит путь, выходящий из узла i,
и выходит путь в узел j, множество путей будет
пустым, а в случае существования такого узла элемент множества Pi,j
(ci,j = Pi,j) будет представлять собой событие прохождения
пути длины 2. Так происходит перебор всех возможных событий. В элемент Pi,j
матрицы М2 войдут все Pi,j, которые будут представлять собой события
прохождения пути единичной длины (обозначим этот элемент со степенью, равной
длине пути, через P1i,j, т.
е. мощность множества [pi,j] равна 1), а также события прохождения пути длины
2, а именно, р2i,j. Подобным образом осуществляем пересечение ![]() и получаем
матрицу М3, содержащую в своих элементах события прохождения
путей длины 1, 2 и 3.
и получаем
матрицу М3, содержащую в своих элементах события прохождения
путей длины 1, 2 и 3.
Рассмотрим случай, когда ориентированных путей длины n в графе нет. В этом случае в матрице Мn получается пересечение множества событий прохождения вершин, принадлежащих всем путям длины n — 1, выходящим из узла i, и множества событий прохождения вершин, принадлежащих путям единичной длины, входящим в узел j. Отсутствие ориентированных путей говорит о том, что нет таких узлов, не принадлежащих уже найденным путям. Таким образом, элементы матрицы останутся неизменными. Это позволяет утверждать, что при последовательном пересечении матриц М и Мn наступит момент, когда Мn станет идентичной Мn-1. Это даст возможность определить все ориентированные пути в графе, причем максимальная длина этих путей будет n-1. Назовем это число предельной степенью матрицы М - р.
По приведенному примеру построим матрицы 2, 3 и 4-й степеней (для
простоты графического отображения матриц ai ![]() aj => aiaj):
aj => aiaj):

При возведении исходной матрицы в пятую степень получим матрицу, полностью аналогичную матрице М4. Это позволяет сказать, что в данном графе нет ориентированных путей длиной, больших 4 (р = 4).
Построим такое множество R, элементами которого
будет совокупность событий прохождения всех путей любой длины. Из полученной
матрицы Мр можно определить элементы множества R: ![]() , где t
= 1,..., p. При попытке найти ориентированный
путь длины на единицу больше (в силу наличия ориентированных циклов длиной
меньше искомых) в множествах Pi,j появляются одинаковые элементы. В этом случае уже
существующие элементы не следует включать в множество. Подобную операцию
(исключение дублирующих уже существующих элементов) необходимо провести и над
множеством R. Ранжируя элементы множества R по их степени, получаем упорядоченное множество
, где t
= 1,..., p. При попытке найти ориентированный
путь длины на единицу больше (в силу наличия ориентированных циклов длиной
меньше искомых) в множествах Pi,j появляются одинаковые элементы. В этом случае уже
существующие элементы не следует включать в множество. Подобную операцию
(исключение дублирующих уже существующих элементов) необходимо провести и над
множеством R. Ранжируя элементы множества R по их степени, получаем упорядоченное множество ![]() . Множество
. Множество ![]() для приводимого
примера определится как: R = {al;
а2; аЗ; а8; a; ala2; ala8; ala3; aa8;
а2а8; ааЗ; a2a8al; aa8al; a8ala3; ala3a; a3aa8; ala8a3a}. Это
множество содержит события прохождения всех ориентированных путей, и по нему
можно разработать оптимальную стратегию тестирования процесса. Данную задачу
можно решить, применяя алгоритм, позволяющий выбрать из набора элементов множества
для приводимого
примера определится как: R = {al;
а2; аЗ; а8; a; ala2; ala8; ala3; aa8;
а2а8; ааЗ; a2a8al; aa8al; a8ala3; ala3a; a3aa8; ala8a3a}. Это
множество содержит события прохождения всех ориентированных путей, и по нему
можно разработать оптимальную стратегию тестирования процесса. Данную задачу
можно решить, применяя алгоритм, позволяющий выбрать из набора элементов множества
![]() (мощности
h) такие, для которых потребовалось бы
минимальное число тестов.
(мощности
h) такие, для которых потребовалось бы
минимальное число тестов.
Третий этап заключается в том, что применяя к полученному
множеству ![]() предлагаемый
алгоритм, можно определить оптимальную стратегию тестирования и минимизировать
количество тестов, обеспечив контроль всех блоков. Алгоритм нахождения
оптимальной стратегии тестирования выполняется над таблицей, строящейся по
результатам анализа элементов множества
предлагаемый
алгоритм, можно определить оптимальную стратегию тестирования и минимизировать
количество тестов, обеспечив контроль всех блоков. Алгоритм нахождения
оптимальной стратегии тестирования выполняется над таблицей, строящейся по
результатам анализа элементов множества ![]() . Ячейки таблицы содержат булевы
переменные y, определяемые по правилу:
. Ячейки таблицы содержат булевы
переменные y, определяемые по правилу:
 (2)
(2)
где ![]() — i-й элемент множества
— i-й элемент множества ![]() мощностью (длина соответствующего
пути) υ;
мощностью (длина соответствующего
пути) υ; ![]() — j-й
элемент множества
— j-й
элемент множества ![]() мощностью w;
i — номер строки таблицы; j
— номер столбца.
мощностью w;
i — номер строки таблицы; j
— номер столбца.
Путей одинаковой длины может быть несколько - в таблицу они заносятся в произвольном порядке. При формальном построении таблицы следует учитывать, что если υ ≥ w, то элемент yi,j - обязательно будет нулевым. Таким образом, столбцы, соответствующие событиям прохождения путей единичной длины, всегда будут нулевыми, и их можно в таблицу не вносить. Построим с помощью правила (2) табл. 1 (заменим выражение "событие прохождения пути" на "путь").
Таблица 1
|
|
← Направление роста длины путей |
|||
|
путь 1 |
путь 2 |
… |
путь h |
|
|
путь 1 |
0 |
y2,1 |
... |
yп,1 |
|
путь 2 |
y1,2 |
0 |
… |
yп,2 |
|
… |
... |
… |
... |
... |
|
путь h |
y1,п |
y2,п |
… |
0 |
Определение необходимого и достаточного набора тестов основано на следующем алгоритме.
Действие алгоритма начинается с крайнего левого столбца (k = 1).
Шаг 1. Проверяем, является ли k-й путь путем единичной длины. Если "да", то переходим на шаг 6. В противном случае — на шаг 2.
Шаг 2. Тестируем k-й путь. Если тест прошел, то — шаг 3, иначе — шаг 5.
Шаг 3. Обнуляем столбцы, соответствующие по номеру строкам, содержащим единицы на пересечении с k-м столбцом. Также обнуляем и эти строки.
Шаг 4. Находим первый слева столбец, содержащий единицы. Если столбец не найден, то переходим на шаг 7, иначе — принимаем k равным номеру найденного пути и переходим на шаг 1.
Шаг 5. Находим первый сверху в k-м столбце единичный элемент и, присваивая k значение номера строки найденного единичного элемента, переходим к шагу 1.
Шаг 6. Тестируем k-й путь. Если тест не прошел, элемент пути признается неисправным и подлежит восстановлению. После восстановления обнуляются k-я строка и k-й столбец и осуществляется переход на шаг 4.
Шаг 7. Все пути протестированы — конец алгоритма.
Применим описанный алгоритм к приведенному примеру (табл. 2). Всем элементам множества
![]() поставим в
соответствие определенный порядковый номер (h = 17).
поставим в
соответствие определенный порядковый номер (h = 17).
Таблица 2
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
п |
al; |
аЗ; |
al; |
а8; |
а; |
а2; |
al; |
al; |
а; |
а2; |
а; |
al; |
а |
а8 |
аЗ |
а2 |
al |
|
у |
а8; |
а; |
аЗ; |
al; |
а8; |
з8; |
а2 |
а8 |
аЗ |
а8 |
а8 |
аЗ |
|
|
|
|
|
|
т |
аЗ; |
а8 |
а |
аЗ |
al |
al |
|
|
|
|
|
|
|
|
|
|
|
|
ь |
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Построим табл. 3 по правилу (2). Полностью нулевые столбцы и строки можно исключить (это возможно вследствие того, что в алгоритме нет операций замены 0 на 1). Последнее, с точки зрения машинной реализации алгоритма, будет означать установку флага "строка пустая" или "столбец нулевой", что заметно упростит просмотр таблицы.
Таблица 3
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
3 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
4 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
5 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
7 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
8 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
9 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
10 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
11 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
12 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
13 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
14 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
|
15 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
16 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
|
17 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
Проделаем на основании примера описанный алгоритм. Будем считать, что события al и а2 влекут за собой ошибку функционирования. Начинаем обработку таблицы с первого столбца.
Выполняются шаги 1 и 2 (тестирование № 1). Тест не проходит — переход на шаг 5. На нем определяем k = 2. Далее шаги 1 и 2 (тестирование № 2). Тест проходит — переход к шагу 3. Обнуляем строки и столбцы с номерами 2, 9, 11, 13, 14, 15. Изменения представлены в табл. 4. Следующий шаг — шаг 4. Определяем k = 1.
Выполняются шаги 1 и 2 (формально должен выполниться тест № 3, но это тот же тест, что и № 1, поэтому временных затрат и затрат на разработку теста на этом шаге не будет). Тест не прошел — переход на шаг 5. На нем определим k = 3. Далее — шаги 1 и 2 (тестирование № 4). Тест не проходит — переход к шагу 5. Определяем k = 12, переходим к шагам 1 и 2. Тестируем путь 12 (тестирование № 5). Тест не проходит. Переходим на шаг 5. Определяем k = 17. Шаги 1 и 6 — тестируем путь 17 (тест № 6). Тест не проходит. Элемент на пути al признается неисправным и восстанавливается.
Обнуляется 17 строка. На шаге 4 определяем k = 1 и переходим к шагам 1 и 2. Проводим тестирование k-го (k = 1) пути (тестирование № 7, затраты только на время тестирования, поскольку тесты для пути 1 уже разработаны). Переходим на шаг 3. Обнуляем строки и столбцы с номерами 1, 3, 4, 5, 8, 12, 17. Изменения представлены в табл. 5. На шаге 4 определяем k = 6 и переходим к шагам 1 и 2. Тестируем путь 6 (тестирование № 8). Тест не проходит. Переходим на шаг 5, определяем k = 7, переходим к шагам 1 и 2. Тестируем путь 7 (тестирование № 9). Тест не проходит — шаг 5. Определяем k = 16. Переходим на шаги 1, 6. Элемент пути 16 тестируется и признается неисправным (тестирование № 10). После восстановления обнуляем 7, 16-ю строки и столбцы и переходим на шаг 4. Определяем путь 6. Переходим на шаги 1, 2. Тестируем уже разработанным тестом текущий путь (тестирование № 11). Тест проходит. На шаге 3 обнуляем строки и столбцы 7 и 10. На шаге 4 очередной путь не найден. Работа алгоритма прекращена.
Таблица 4
|
|
1 |
3 |
4 |
5 |
6 |
7 |
8 |
10 |
12 |
|
3 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
4 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
5 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
7 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
8 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
10 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
12 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
16 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
|
17 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
Отметим, что в случае присутствия в схеме одиночной ошибки, например только в случае выполнения события а2, то сразу после прохождения шагов 1, 2, 3 мы получаем (протестировав только один путь) табл. 5.
Таблица 5
|
|
6 |
7 |
10 |
|
7 |
1 |
0 |
0 |
|
10 |
1 |
0 |
0 |
|
16 |
1 |
1 |
1 |
В результате применения алгоритма было проведено 11 тестирований, для которых было разработано семь тестов. Для полного тестирования системы (без применения данной стратегии), потребовалось бы 17 тестов и 17 тестирований.
Расписав для всех событий, соответствующих выполнению отдельных блоков,
поле элементарных событий, для элементов множества ![]() можно определить
подмножества этого поля. Этим определятся условия выполнения событий
прохождения путей неединичной длины, а по существу, необходимые для построения
тестового воздействия данные (например, определенный набор данных,
обеспечивающих переход по нужной ветке блока ветвления).
можно определить
подмножества этого поля. Этим определятся условия выполнения событий
прохождения путей неединичной длины, а по существу, необходимые для построения
тестового воздействия данные (например, определенный набор данных,
обеспечивающих переход по нужной ветке блока ветвления).
Таким образом, предложенный метод работает на детерминированных тестовых наборах и позволяет оценить систему по выбранному критерию. Он вполне может быть использован при диагностических испытаниях топологических систем (в частности, в режиме STM — system test mode [11]). Кроме того, он определяет необходимое число поэлементного пересечения матриц исходя не из количества узлов (что было верно только для последовательных графов), а из длины максимального ориентированного цикла в графе, что позволяет применить его и к системам с обратными связями.
Предлагаемый подход применим не только на этапе тестирования, но и на
этапе разработки систем. Получение множества ![]() даст возможность на этапе
проектирования оптимальным образом скорректировать структуру и состав системы.
При этом он достаточно просто реализуем на ЭВМ.
даст возможность на этапе
проектирования оптимальным образом скорректировать структуру и состав системы.
При этом он достаточно просто реализуем на ЭВМ.
Описанный алгоритм работает в духе концепции кольцевого тестирования [14], когда генератор тестов и анализатор реакций тестируемого объекта представляют единое целое. Это позволит сократить не только трудозатраты на написание тестов, но и время тестирования.
Приведенный способ проведения диагностирования сложных систем позволяет формализовать процесс диагностирования и может быть реализован на ЭВМ (например, с использованием алгоритмических языков, оперирующих символьными элементами, таких как ЛИСП или ФОРТ).
Список литературы
1. Тестовое диагностирование логических структур / В. А. Полипейко, И. А. Анучин, В. К. Жуляков, В. О. Плокс, Я. П. Круминь. Под ред. В. А. Полипейко. — Рига: Зинатне, 1986. 262 с.
2. Roth J. P. Diagnosis of Automata Failures: A Calculus and A Method // IBM Journal of Research and Development, 1966. N 10. P. 278-291.
3. Кривуля Г. Ф., Немченко В. П., Шкиль А. С. Построение диагностического теста цифрового устройства на этапе проектирования // Вопросы технической диагностики. Ростов н/Д: Изд. Рост, инж.-строит. ин-та, 1981. С. 20—28.
4. Кривуля Г. Ф., Немченко В. П. Диагностика цифровых вычислительных машин. Харьков: Изд. ХПИ, 1985. 71 с.
5. Барабаш И. П., Тимонькин Т. Н., Ткаченко С. Н., Харченко В. С. Синтез микропрограммных генераторов тестов / Вопросы технической диагностики. — Ростов н/Д: Изд. Рост, инж.-строит. ин-та, 1981. С. 16—20.
6. Тоценко В. Г. Алгоритмы технического диагностирования дискретных устройств. М.: Радио и связь, 1985. 240 с.
7. Савченко Ю. Г. Цифровые устройства, нечувствительные к неисправностям элементов. М.: Сов. радио, 1977. 176 с.
8. Драч Г. А. Диагностическая модель с применением полюсных графов // Вопросы технической диагностики. Ростов н/Д: Изд. Рост, инж.-строит. ин-та, 1981. С. 38—41.
9. Алгоритмы и программы решения задач на графах и сетях / И. М. Нечепуренко, В. К. Попков, С. М. Майнагашев и др. Новосибирск: Наука. Сиб. отд-ние, 1990. 515 с.
10.Граф Ш., Гессель М. Схемы поиска неисправностей: Пер. с нем. М.: Энергоатомиздат, 1989. 144 с.
11. Цзуй Ф. Ф. Испытания in situ (ISTD) — новый метод проверки быстродействующей БИС/СБИС-логики: Пер. с англ. // ТИИЭР. 1982. Т. 70, № 1. С. 75—98.
12. Кудрявцев А. В., Алаев И. В., Фрид А. И. Оптимизация архитектур устройств ввода информационно-управляющих комплексов бортовых вычислительных систем по критериям надежности // Проблемы совершенствования робототехнических и интеллектуальных систем летательных аппаратов. М.: Изд-во МАИ, 1996. С. 67—70.
1З.Хетагуров Я. А., Древе Ю. Г. Проектирование информационно-вычислительных комплексов: Учеб. для вузов по спец. "АСУ". М.: Высшая школа, 1987. 280 с.
14.Литиков И. П. Кольцевое тестирование цифровых устройств. М.: Энергоатомиздат, 1990. 160 с.
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 3, 1998
СИСТЕМЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ
Ключевые слова Теория систем, сложные системы, тестирование, диагностика, структуры систем, теория графов, матричные модели, алгоритмы, критерии оценки.
Публикации с ключевыми словами: критерии оценки, тестирование, алгоритмы, Теория систем, сложные системы, диагностика, структуры систем, теория графов, матричные модели
Публикации со словами: критерии оценки, тестирование, алгоритмы, Теория систем, сложные системы, диагностика, структуры систем, теория графов, матричные модели
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



