научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2012
DOI: 10.7463/1012.0478399
УДК: 621.396.662
Россия, МГТУ им. Н.Э. Баумана
Введение
Системы фазовой автоподстройки (ФАП) находят широкое применение в различных областях техники: слежение за несущими и поднесущими частотами принимаемых сигналов, когерентная демодуляция сигналов с частотной и фазовой модуляцией, измерение частоты и фазы сигналов и т.д.
Для анализа дискретных ФАП применяются интегральное уравнение Колмогорова-Чепмена и уравнение среднего времени до срыва синхронизации [1-3]. В указанных работах найдены плотности распределения вероятности (ПРВ) координат, в меньшей степени исследованы характеристики срыва слежения, причем рассмотрены непрерывные системы, и не проводится анализ дискретных ФАП.
В данной статье приводится анализ срыва синхронизации дискретных ФАП 1-го и 2-го порядков различными методами.
1. Постановка задачи
Срыв слежения в непрерывной ФАП, которая описывается системой стохастических ДУ 2-го порядка, представляет собой до настоящего времени в общем случае нерешенную задачу. Корректно эта задача должна быть решена как краевая задача для уравнения Понтрягина [4]. Пусть М - диффузионный оператор Понтрягина. Т - среднее время до срыва слежения, ![]() - граница области D фазового пространства. Срыв слежения происходит тогда и только тогда, если изображающая точка выходит за границу
- граница области D фазового пространства. Срыв слежения происходит тогда и только тогда, если изображающая точка выходит за границу ![]() области D фазового пространства. При этом среднее время до срыва удовлетворяет краевой задаче
области D фазового пространства. При этом среднее время до срыва удовлетворяет краевой задаче
MT = -1 в области D; Т = 0 на границе![]() . (1)
. (1)
Однако трудность заключается в правильном выборе краевых условий, чего корректно до сих пор не сделано. Поэтому приходится прибегать к более простым методам вычисления времени до срыва слежения.
Можно, в частности, использовать приближенные формулу Крамepca и формулу Журавлева для ФАП с интегрирующим фильтром (ИФ), а также формулу [5] для ФАП с пропорционально-интегрирующим фильтром (ПИФ). Имеются приближенные выражения для среднего времени до срыва, которые получили Таусворт [6] и Линдсей. Кроме того, для приближенного вычисления среднего времени до срыва слежения могут быть использованы метод усреднения и другие асимптотические методы.
Анализ срыва слежения в непрерывных системах автоматического регулирования второго порядка рассмотрен в ряде работ [6, 7 и др.]. Некоторые неудобства при сопоставлении результатов представляет различная нормировка среднего времени Тс до срыва синхронизации, так, например, Шухман [7] нормирует по шумовой полосе (![]() ), Таусворт [6] и Линдсей - по удвоенной шумовой полосе (
), Таусворт [6] и Линдсей - по удвоенной шумовой полосе (![]() ), в статье отдается предпочтение нормировке
), в статье отдается предпочтение нормировке ![]() при у(х) = sin(х), переходящую в нормировку по полосе синхронизации в системе 1-го порядка [8]. В данной статье вначале рассматриваются приближенные соотношения для среднего времени до срыва слежения, а затем решается краевая задача.
при у(х) = sin(х), переходящую в нормировку по полосе синхронизации в системе 1-го порядка [8]. В данной статье вначале рассматриваются приближенные соотношения для среднего времени до срыва слежения, а затем решается краевая задача.
2. Приближенные методы анализа
Метод Таусворта (метод аппроксимации условного среднего значения ![]() ). Данный метод используется как для аппроксимации коэффициентов сноса и диффузии в уравнении Понтрягина [6], так и для аппроксимации решения этого уравнения. Рассмотрим вначале первый способ решения задачи: в [6] показано, что в случае ФАП 2-го порядка можно использовать дифференциальное уравнение (ДУ) Понтрягина в форме [6]
). Данный метод используется как для аппроксимации коэффициентов сноса и диффузии в уравнении Понтрягина [6], так и для аппроксимации решения этого уравнения. Рассмотрим вначале первый способ решения задачи: в [6] показано, что в случае ФАП 2-го порядка можно использовать дифференциальное уравнение (ДУ) Понтрягина в форме [6]
![]() (2)
(2)
Здесь оператор Понтрягина

![]() - коэффициент сноса;
- коэффициент сноса; ![]() - коэффициент диффузии;
- коэффициент диффузии;

Решение Т(х0), как и в системе 1-го порядка, должно удовлетворять граничным условиям (1)
![]() (3)
(3)
Запишем ДУ (2) в форме [6]
![]() (4)
(4)
где ![]()
В [7] по методу Таусворта получено обобщенное ДУ Понтрягина.
Это ДУ при наличии вырожденного ПИФ (ВПИФ) имеет вид
![]() Т (5)
Т (5)
где ![]() а граничные условия аналогичны (3)
а граничные условия аналогичны (3)
![]()
При вычислении ![]() и
и ![]() целесообразно в общем случае численно решать краевую задачу (1) методом прогонки.
целесообразно в общем случае численно решать краевую задачу (1) методом прогонки.
Разбивая отрезок ![]() на N участков длиной
на N участков длиной ![]() точками
точками ![]() полагая
полагая ![]() и заменяя производные конечными разностями, при
и заменяя производные конечными разностями, при ![]() имеем [8]
имеем [8]
![]() (6)
(6)
где ![]() граничные условия
граничные условия ![]()
Для системы 1-го порядка ДУ (2), (4) являются точными, для системы 2-го порядка - приближенными за счет приближенного вычисления коэффициентов сноса и диффузии.
Найдем решение ДУ (4). Запишем (4) в форме ДУ 1-го порядка [8]
dz/dx + p(x)z = q(х),
где z = dT/dx; р(х) = 2а(х)/b(х); q(х) = -2/b(х).
Решением этого ДУ служит
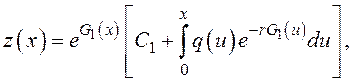
где  Отсюда
Отсюда ![]()
Общее решение ДУ (4) имеет вид
 (7)
(7)
где ![]()
 Постоянная
Постоянная ![]() определяется из граничного условия
определяется из граничного условия ![]() :
:

в результате получаем решение ДУ Понтрягина
 (8)
(8)
Постоянная C1 находится из второго граничного условия ![]() :
:

В результате окончательно находим решение ДУ (4), удовлетворяющее граничным условиям (3)

Символическая форма ДУ ФАП имеет вид [6]
![]()
Замечаем, что полоса синхронизации ![]()
Согласно методу Таусворта
![]()
где ![]() - односторонний энергетический спектр белого шума
- односторонний энергетический спектр белого шума ![]()
![]()
Для системы 1-го порядка
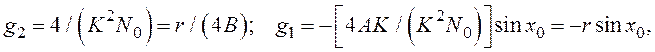 (9)
(9)
где ![]()
Пусть фильтр низких частот представляет собой ВПИФ ![]() , тогда
, тогда
![]()
где ![]()
Односторонняя шумовая полоса В линеаризованной ФАП имеет вид [8]

где ![]()
Отсюда, если ![]() получаем шумовую полосу ФАП с ВПИФ
получаем шумовую полосу ФАП с ВПИФ
![]() (10)
(10)
При наличии ПИФ F = а,

При ![]() находим коэффициент
находим коэффициент ![]() для ФАП с ВПИФ
для ФАП с ВПИФ
 (11)
(11)
где ![]() .
.
Найдем величину ![]() . Согласно [6]
. Согласно [6]
![]()
где ![]() .
.
Если ограничиться линейным членом разложения, то можно получить выражение [6]
![]()
где находим  Отсюда при
Отсюда при ![]() находим
находим ![]() Тогда
Тогда
![]()
Коэффициент
![]()
где 
Если ПИФ вырожденный (l = 1), то
![]() (12)
(12)
С учетом приведенных значений коэффициентов уравнения Понтрягина имеем
![]()
Следовательно, 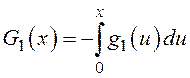 является функцией четной. Отсюда следует, что функция
является функцией четной. Отсюда следует, что функция ![]() в (8) и (9) является нечетной функцией. В дальнейшем рассматриваются границы
в (8) и (9) является нечетной функцией. В дальнейшем рассматриваются границы ![]() симметричные относительно начала координат, поэтому постоянная
симметричные относительно начала координат, поэтому постоянная ![]() В этом частном случае по (9) находим среднее время достижения порога [8]:
В этом частном случае по (9) находим среднее время достижения порога [8]:
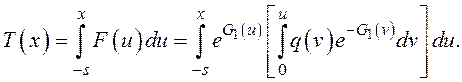
Учтем равенство
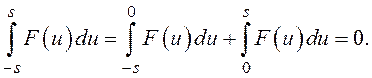
Тогда получаем
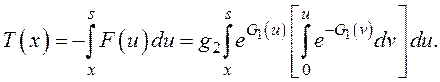
Полагая ![]() и используя выражение (11), (12) для коэффициентов
и используя выражение (11), (12) для коэффициентов ![]() и
и ![]() , находим среднее время достижения порога в системе 2-го порядка с ВПИФ
, находим среднее время достижения порога в системе 2-го порядка с ВПИФ

где 
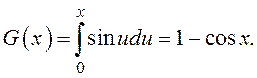
При выполнении условия ![]() получаем
получаем
 (13)
(13)
При ![]() по (13) находится точное значение среднего времени достижения порога в системе 1-го порядка при нулевой начальной расстройке [8, формула (1.85)]. Значение
по (13) находится точное значение среднего времени достижения порога в системе 1-го порядка при нулевой начальной расстройке [8, формула (1.85)]. Значение ![]() можно найти, используя разностную схему ДУ Понтрягина (6).
можно найти, используя разностную схему ДУ Понтрягина (6).
Вычисленная таким образом зависимость ![]() изображена на рис. 1 а при
изображена на рис. 1 а при ![]() и рис. 1 б при отношении помеха/сигнал
и рис. 1 б при отношении помеха/сигнал ![]() и различных значениях
и различных значениях ![]() . Сравнивая рис. 1 а и рис. 1 б, замечаем, что при больших значениях отношения сигнал/шум (ОСШ)
. Сравнивая рис. 1 а и рис. 1 б, замечаем, что при больших значениях отношения сигнал/шум (ОСШ) ![]()
![]() (рис. 1 а),
(рис. 1 а), ![]() (рис. 1 б),
(рис. 1 б),
в последнем случае, как и для системы 1-го порядка [8]. На рис. 1 а, б: 1- ![]() =8, 2-
=8, 2- ![]() =4, 3-
=4, 3-![]() = 2, 4-
= 2, 4- ![]() =1, 5-
=1, 5- ![]() =0,5, 6-
=0,5, 6- ![]() =0,1; на рис. 1 а: 7 -
=0,1; на рис. 1 а: 7 -![]() =20.
=20.
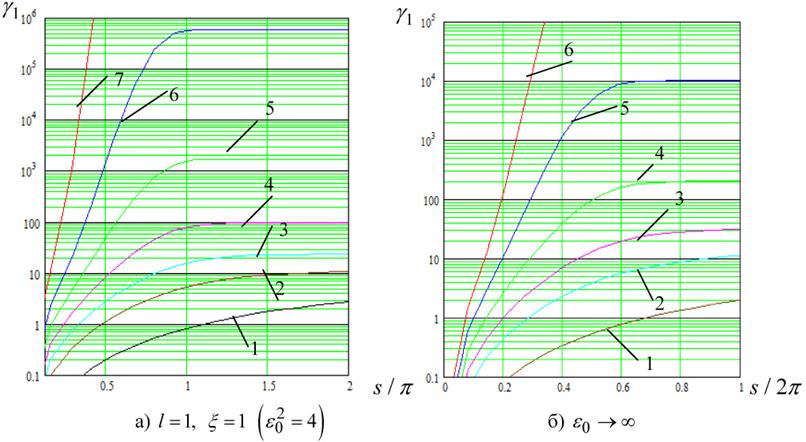
Рис. 1. Среднее время достижения порога в системе 1 порядка при нулевой начальной расстройке
При больших значениях ![]() независимо от величины
независимо от величины ![]() справедлива приближенная формула для моментов времени
справедлива приближенная формула для моментов времени ![]() до срыва слежения [8]
до срыва слежения [8]
![]() (14)
(14)
Справедливость этой формулы доказана в [8] для ФАП 1-го порядка. С ростом ![]() при
при ![]() значения
значения ![]() асимметрии
асимметрии ![]() и эксцесса
и эксцесса ![]() попадают в интервал, определяемый для системы 1-го порядка [8]:
попадают в интервал, определяемый для системы 1-го порядка [8]:
![]()
При аппроксимации решения уравнения Понтрягина Таусворт получил формулу [6, формула (18)]
 (15)
(15)
где

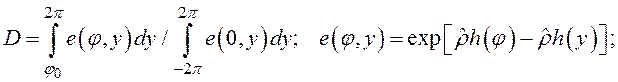
![]()
![]()
При больших ![]() и малых
и малых ![]() формула (15) дает большую погрешность.
формула (15) дает большую погрешность.
Асимптотические методы. Для ФАП с ИФ при малой постоянной времени фильтра или, что эквивалентно, при большом значении величины ![]() можно воспользоваться приближенным соотношением
можно воспользоваться приближенным соотношением
![]() , (16)
, (16)
причем величина ![]() может быть вычислена по формуле Журавлева.
может быть вычислена по формуле Журавлева.
В результате получаем
![]() (17)
(17)
где  ([8]); W(х) - ПРВ системы 1-го порядка.
([8]); W(х) - ПРВ системы 1-го порядка.
На рис. 2 зависимость (17) изображена сплошными линиями при ![]() = 2, 5, здесь же крестиками обозначены значения
= 2, 5, здесь же крестиками обозначены значения ![]() , вычисленные по формуле (17), когда величина рассчитывалась методом матричной прогонки; штриховыми линиями на рис. 2 изображена зависимость
, вычисленные по формуле (17), когда величина рассчитывалась методом матричной прогонки; штриховыми линиями на рис. 2 изображена зависимость ![]() для системы 1-го порядка [8]
для системы 1-го порядка [8]
 (18)
(18)
где ![]() .
.
При наличии ПИФ справедлива система стохастических ДУ, из первого уравнения которой при ![]()
![]() получаем ДУ
получаем ДУ
![]() (19)
(19)
т.е. ДУ ФАП 1-го порядка, отличающееся параметром ![]() и
и ![]() .
.
При ![]()
тогда среднее значение частотного рассогласования
![]()
где ![]() - среднее значение величины
- среднее значение величины ![]() при усреднении с весом ПРВ W1(x), которая отличается от W(x) системы 1-го порядка значением
при усреднении с весом ПРВ W1(x), которая отличается от W(x) системы 1-го порядка значением ![]() : W1(x) получается из W(x) заменой r на
: W1(x) получается из W(x) заменой r на ![]() и
и ![]() . Следовательно, все формулы, справедливые для системы 1-го порядка, оказываются асимптотическими для системы 2-го порядка с ПИФ при
. Следовательно, все формулы, справедливые для системы 1-го порядка, оказываются асимптотическими для системы 2-го порядка с ПИФ при ![]() Формула для среднего времени до срыва слежения принимает вид
Формула для среднего времени до срыва слежения принимает вид
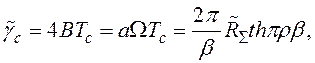
где 
Эта зависимость в форме ![]()
![]() изображена на рис. 2.
изображена на рис. 2.
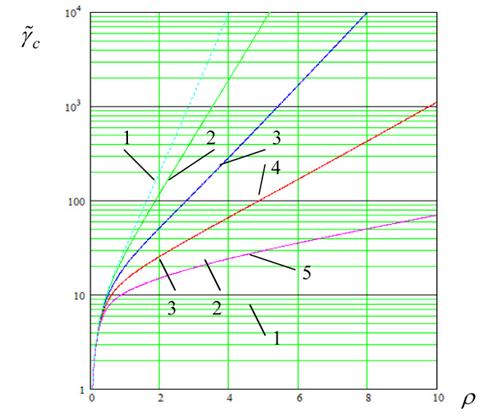
Рис. 2. Зависимость среднего времени от ОСШ для дискретной ФАП 2-го порядка с невырожденным ФАП асимптотическим методом
1- ![]() 0; 2-
0; 2- ![]() 0,2; 3-
0,2; 3- ![]() 0,4; 4-
0,4; 4- ![]() 0,6; 5-
0,6; 5- ![]() 0,8
0,8
По (13) можно получить асимптотические формулы, справедливые при малых и больших значениях ![]() .
.
При ![]() используя приближенные равенства
используя приближенные равенства ![]() находим
находим
 (20)
(20)
При ![]()
![]() для системы 1-го порядка [8];
для системы 1-го порядка [8]; ![]() Тогда приближенная формула для среднего времени до срыва слежения принимает вид
Тогда приближенная формула для среднего времени до срыва слежения принимает вид
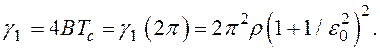 (21)
(21)
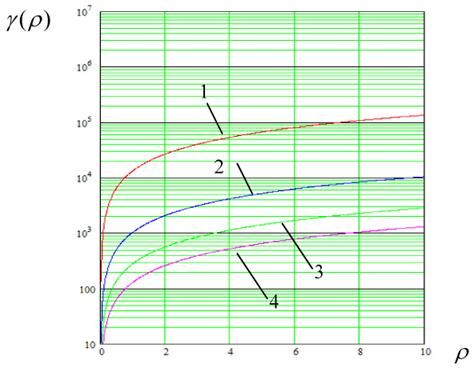
Рис. 3. Зависимость среднего времени от ОСШ для дискретной ФАП 1-го порядка асимптотическим методом: 1- ![]() 0,2; 2-
0,2; 2- ![]() 0,4; 3-
0,4; 3- ![]() 0,6; 4-
0,6; 4- ![]() 0,8.
0,8.
Значения ![]() , рассчитанные по этой формуле, при
, рассчитанные по этой формуле, при ![]() =0,1 и соответственно
=0,1 и соответственно ![]() = 2; 4; 10; 1000 равны 4,4413 (3,3759); 3,0842 (2,6731); 2.3884 (2,2575); 1,9778 (1,9865) (в скобках указаны точные значения). Таким образом, точность приближенной формулы растет с ростом
= 2; 4; 10; 1000 равны 4,4413 (3,3759); 3,0842 (2,6731); 2.3884 (2,2575); 1,9778 (1,9865) (в скобках указаны точные значения). Таким образом, точность приближенной формулы растет с ростом ![]() .
.
Пусть ![]() , тогда подынтегральные функции в (13) имеют острые максимумы: во внутреннем интеграле в точке
, тогда подынтегральные функции в (13) имеют острые максимумы: во внутреннем интеграле в точке ![]() , во внешнем – в точке
, во внешнем – в точке ![]() причем
причем ![]() и
и ![]() находятся из уравнения
находятся из уравнения ![]() или
или
![]()
Следовательно, ![]() =0, а
=0, а ![]() можно вычислить, используя приближенное равенство
можно вычислить, используя приближенное равенство ![]()
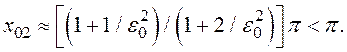
Имея в виду острый максимум в точке ![]() воспользуемся отрезком ряда
воспользуемся отрезком ряда
![]()
тогда приближенно можно вычислить внутренний интеграл в (13)
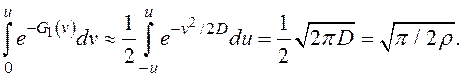
Остается вычислить внешний интеграл в (13), используя разложение во втором остром максимуме

![]()
В результате находим приближенное значение внешнего интеграла (13)

Таким образом, приближенная формула для среднего времени до срыва слежения для ФАП с ВПИФ с учетом (13) и равенства ![]() принимает вид
принимает вид
 (22)
(22)
где 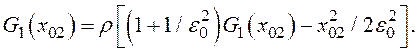
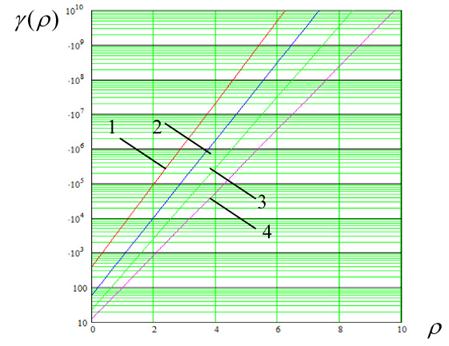
Рис. 4 Зависимость среднего времени от ОСШ для дискретной ФАП с ВПИФ асимптотическим методом: 1- ![]() 0.2; 2-
0.2; 2- ![]() 0.4; 3-
0.4; 3- ![]() 0.6; 4-
0.6; 4- ![]() 0.8.
0.8.
Отсюда при ![]() следует известное приближенное равенство (14).
следует известное приближенное равенство (14).
Запишем полученное соотношение в виде произведения
![]() (23)
(23)
где 
![]()
Сравним результаты вычислений ![]() по формуле (4.23) и точные данные (указаны в скобках). При
по формуле (4.23) и точные данные (указаны в скобках). При ![]() =2; 4; 10 соответственно получаем: при
=2; 4; 10 соответственно получаем: при ![]() 2 – 47,2 (74,2); 70,8 (37,9); 110 (138); при
2 – 47,2 (74,2); 70,8 (37,9); 110 (138); при ![]() - 1,59·103 (2,28·103); 5,88·103 (7,32·103); 2,08·104 (2,33·104). Как видно, относительная погрешность превышает 36% и 30% соответственно при
- 1,59·103 (2,28·103); 5,88·103 (7,32·103); 2,08·104 (2,33·104). Как видно, относительная погрешность превышает 36% и 30% соответственно при ![]() ,
, ![]() и уменьшается с ростом
и уменьшается с ростом ![]() . Для сравнения отметим, что погрешность (4.14) составляет 21 %, 17%, 5% соответственно при
. Для сравнения отметим, что погрешность (4.14) составляет 21 %, 17%, 5% соответственно при ![]() и 5.
и 5.
В качестве оценки времени до срыва слежения может быть использована формула
![]()
где ![]() - частота достижения уровня
- частота достижения уровня ![]() фазовым случайным процессом.
фазовым случайным процессом.
При ![]() получаем
получаем
![]() (24)
(24)
Это же равенство находится по формуле Крамерса при ![]() и
и ![]()
3. Срыв слежения в системе с интегрирующим фильтром
На рис. 5 изображены графики зависимости среднего времени до срыва слежения от параметров системы при r=1; 2 и ![]() Кривые 1 и 2 соответствуют первой формуле Крамерса.
Кривые 1 и 2 соответствуют первой формуле Крамерса.
Метод Крамерса (малая расстройка ![]() и значительная величина ОСШ r). При вычислении среднего времени в системе с ИФ воспользуемся формулой Крамерса. При
и значительная величина ОСШ r). При вычислении среднего времени в системе с ИФ воспользуемся формулой Крамерса. При ![]() формула Крамерса для нормированной величины среднего времени
формула Крамерса для нормированной величины среднего времени ![]() принимает вид
принимает вид
![]() (25)
(25)
где 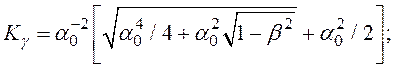
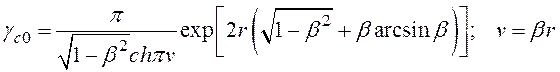 (26)
(26)
Кривые 3 и 4 соответствуют второй формуле Крамерса
![]() (27)
(27)
где ![]()
![]()
В крайних точках параметра ![]() численным методом получены следующие результаты: при r=1
численным методом получены следующие результаты: при r=1 ![]() если
если ![]() и
и ![]() если
если ![]() при r=2
при r=2 ![]() если
если ![]() и
и ![]() если
если ![]() .
.
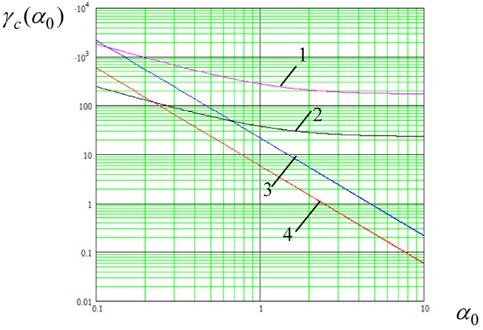
Рис. 5. Зависимости среднего времени от срыва слежения от параметров системы численным методом при ![]() 1, 2 – соответствует 1-ой формуле Крамерса,
1, 2 – соответствует 1-ой формуле Крамерса,
3, 4 – 2-ой формуле Крамерса; 1, 3 - r=1; 2, 4 - r=2.
На рис. 5 замечаем, что при малых ![]() результаты ближе ко 2-ой формуле Крамерса, а при умеренных
результаты ближе ко 2-ой формуле Крамерса, а при умеренных ![]() результаты численного метода совпадают с данными, полученными по 1-ой формуле Крамерса, и при
результаты численного метода совпадают с данными, полученными по 1-ой формуле Крамерса, и при ![]()
![]() среднее время до срыва стремится к асимптоте, характеризующей систему 1-го порядка. Кроме того, замечаем, что с уменьшением
среднее время до срыва стремится к асимптоте, характеризующей систему 1-го порядка. Кроме того, замечаем, что с уменьшением ![]() сближаются средние времена достижения порогов
сближаются средние времена достижения порогов ![]() и
и ![]() .
.
Заключение
Таким образом, в результате проведенного анализа были получены сравнительные характеристики среднего времени до срыва синхронизации приближенными методами в зависимости от значений отношения сигнал/шум и отношения помеха/сигнал. Представлены полученные результаты для ФАП 1-го и 2-го порядков. Получены характеристики для ФАП с ПИФ и ВПИФ.
Список литературы
1. Chie C.M. Mathematical analogies between first-order digital and analog phase-locked loops // IEEE Trans. 1978. Vol. COM-26, № 6. P. 860-865. DOI: 10.1109/TCOM.1978.1094148
2. Weinberg A., Liu B. Discrete time analysis of nonuniform sampling first- and second- order phase-locked loops // IEEE Trans. 1972. Vol. COM-22, № 2. P. 123-137. DOI: 10.1109/TCOM.1974.1092168
3. Битюцкий В.И., Сердюков П.Н. Оценка времени до срыва синхронизма в импульсной системе ФАПЧ // Радиотехника. 1973. № 8. С. 95-97.
4. Тихонов В.И., Миронов М.А. Марковские процессы. М.: Советское радио, 1977.525 с.
5. Шахтарин Б.И. Статистическая динамика систем синхронизации. М.: Радио и связь, 1998. 488 с.
6. Tausworthe R.C. Cycle slipping in phase-locked loops // IEEE Trans. on Communications. 1967. Vol. COM-15, № 3. P. 417-421.
7. Schuchman L. Time to cycle slip in first and second order phase locked loop // Inter. Comm. Conf. San-Francisco. 1970. P. 341-349.
8. Шахтарин Б.И. Анализ систем синхронизации при наличии помех. М.: ИПРЖР, 1996. 252 с.
Публикации с ключевыми словами: дискретная система, фазовая автоподстройка, среднее время, срыв слежения, приближенные методы, формула Крамерса
Публикации со словами: дискретная система, фазовая автоподстройка, среднее время, срыв слежения, приближенные методы, формула Крамерса
Смотри также:
- Срыв синхронизации в системе слежения за задержкой псевдошумового сигнала
- 77-30569/296014 Среднее время до срыва слежения и среднее значение частотного рассогласования фазовой автоподстройки при наличии комбинированного воздействия
- 77-48211/359541 Статистическая динамика фазовой автоподстройки второго порядка при воздействии комбинированных помех
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



