научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#7 июль 2004
Бодякин В.И., Чистяков А.А.
АССОЦИАТИВНЫЕ
ИНФОРМАЦИОННЫЕ
СТРУКТУРЫ и МОДЕЛИ
ПАМЯТИ.
АННОТАЦИЯ
На основе формального определения информационного потока и типов его информационных структур – линейной, древовидной и сетевой, введено формальное определение ассоциативности элементов связной структуры. Показано, что каждому типу структуры соответствует своя модель памяти. Рассмотрены свойства этих структур и отображения на них фрагмента потока. Доказано, что полной ассоциативностью и оптимальными свойствами обладает иерархически-сетевая модель структуры памяти, функциональным аналогом которой является нейросемантическая структура. Рассмотрены области применения ассоциативных структур и нейросемантичесчких моделей памяти.
Введение
Информационные технологии, как никакие другие, вобрали в себя и реализовали множество передовых идей и открытий, но при этом сохранили практически в неприкосновенности принцип доступа по адресу к хранимой информации. Этот принцип заключается в том, что подавляющем большинстве устройств хранения данных обращаться к содержимому можно только через конкретный адрес. А именно он является, по мнению авторов, главным препятствием при создании современных высокопроизводительных и сложных информационных систем.
Альтернативой адресной памяти является ассоциативная память (АП). Проблемам построения моделей АП и ее реализации посвящены обширные публикации, в частности, [1, 2, 3, 4, 5]. В АП доступ осуществляется «исходя из содержания хранимой информации», кроме того, он возможен «ко всей хранящейся информации». При этом подразумевается, что при предъявлении некоторого содержимого (или фрагмента) в виде поискового образа необходимо найти точный адрес или другой однозначный идентификатор, с помощью которого можно осуществить доступ к более обширному информационному содержанию, чем образ. На программном (логическом) уровне этот принцип (привязка содержимого к адресу) в настоящее время реализован для некоторого класса узких задач с помощью механизма индексирования в базах данных (БД). Они ассоциативны только на уровне содержимого некоторых таблиц БД и только для заранее предусмотренных свойств и содержаний. Поэтому их можно назвать частично ассоциативными, т.к. доступ реализован через файловую систему (ФС) в простой форме и на ограниченном объеме данных.
Ассоциативный доступ непосредственно зависит от содержимого, он возможен только при наличии данных в устройстве, поэтому, моделировать и строить устройства АП без учета свойств самих данных, не представляется возможным. Наиболее современная модель такой памяти, которая строится исходя из объективных общих свойств содержащейся в них информации, приведена в [6, 7, 8, 9]. Она представлена в виде функциональной нейроноподобной среды с сетевой структурой семантических элементов.
В современных системах обработки информации имеют дело с постоянно поступающими на устройства хранения большими объемами данных, которые можно определить как поток данных. Ближайшим аналогом потока является текстовая последовательность символов, текстовая форма представления информации [6, 7, 8, 9], множество сообщений, принимаемое получателем и т.п. Единицей может быть символ, морфема, слово, словосочетание, строка, абзац и пр. В данной работе будем придерживаться этой лингвистической метафоры [4, 6, 7, 8, 9], как широко распространенной и удобной для понимания и изложения.
Определение 1. Потоком данных называется упорядоченная последовательность знаков, в виде строки I = { i i1, i2, ... , iL} конечной длины размером в L символов. В дальнейшем такую строку I будем также называть исходный текст, или просто текст.
Поток определен на конечном алфавите B ={bm}, т.е. в качестве минимальной информационной единицы рассматривается символ алфавита
"ik О I $ ! bj О B ® ik = bj , (1.1)
и
" bj О B $ ~! ik О I ® bj = ik, (1.2)
Выражения (1.2) указывают на то, что символу алфавита соответствует не всегда единственный элемент потока, или, что один и тот же символ может встречаться в потоке много раз.
Всегда будем считать, что размер потока существенно больше размера алфавита, т.е.
L >>|B| (1.3)
Вследствие этого в тексте должна присутствовать повторяемость, как отдельных символов алфавита, так и их устойчивых сочетаний. Повторяемость является одним из основных качеств, на котором основываются прикладные свойства информационных структур. Примером таких статистически устойчивых сочетаний присутствующих в тексте согласно лингвистической метафоре являются слоги, корни слов, слова и словосочетания в естественном языке. При этом более мелкие элементы содержатся в более крупных, или принадлежат им.
Определение 2. Информационной структурой данных называется взаимнооднозначное отображение элементов потока данных I на граф T=(S, U), где S={s} множество вершин или узлов, а U={u} это множество соединяющих их дуг. Каждому элементу структуры (вершине или дуге) соответствует ее информационное содержание или обратное отображение на поток. Связи в графе структуры отражают отношения вхождения (принадлежности) между различными информационными элементами данных и пути доступа к ним.
Информационная структура служит основой для моделирования механизмов памяти, хранения, поиска, доступа к данным.
Ассоциативную информационную структуру определим как структуру, в которой любой фрагмент потока F Н I, взаимнооднозначно соответствует непустому подмножеству элементов связной структуры, построенной на всем потоке I. Модель ассоциативной памяти должна содержать в себе механизм отображения содержимого фрагмента-образа F на адрес-идентификатор элемента (элементов) в связной структуре потока. Рассмотрим наиболее интересные с точки зрения моделей АП виды структур.
1. Линейные структуры
Поток данных может быть отображен на множество адресов в обобщенной модели устройства хранения данных. Каждому адресу такого устройства соответствует его информационное содержание (т.е. конкретные данные, которые хранятся в ячейке с этим адресом). Сразу отметим, что это не есть взаимнооднозначное соответствие, так как одинаковые данные могут одновременно находиться в различных ячейках устройства (см. условие 1.1 и 1.2). Для упрощения будем считать, что в одной ячейке хранится один символ потока.
Если каждому символу потока или адресу ячейки в устройстве хранения поставить в соответствие вершину графа структуры, то получим линейно упорядоченное множество вершин без связей, или, так называемую, линейную структуру (см. рис 1).
Для линейной структуры множество дуг U пусто, граф несвязен, а потоку I соответствует только множество упорядоченных вершин S и |S|=L. Таким образом, для линейной структуры имеем I « S. Граф такого вида называется груда [10]. Существование его графа очевидно.
Информационным содержанием I(sm) вершины smОS является однозначно соответствующий ей символ потока im , т.е. I (sm)=im (см. рис 1, 2).
Ниже, при анализе других видов структур, нам потребуется учет порядка следования дуг, подходящих к одному узлу (сверху вниз или слева направо, как на рис 4). Для более наглядного отображения такого порядка, вершины или узлы графа будем изображать не в виде традиционных окружностей или точек, а в виде треугольников.
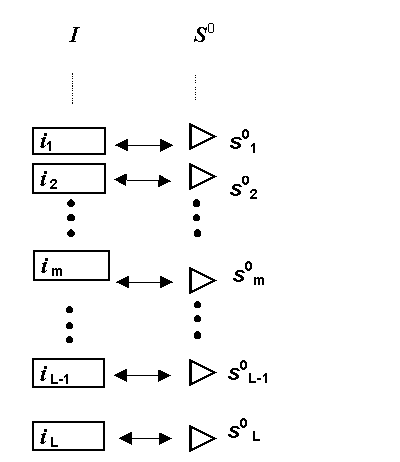
Рис. 1. Граф линейной структуры потока данных
Отсюда следует, что просто линейная модель памяти, как и устройства на ее базе, без дополнительных программно-логических преобразований, непосредственно не годятся для АП, в силу несвязности информационных содержаний элементов ее структуры. Для решения проблемы построения модели АП необходимо исследовать структуры более высокой степени сложности, такие, как древовидные и сетевые.
2. Древовидные структуры
Следующей по распространенности является древовидная структура, которая положена в основу всех известных файловых систем (ФС). В ФС с помощью идентификатора вершины соответствующей файлу (имени файла), возможен доступ к его информационному содержанию. В древовидной структуре, как и в линейной, выполняется однозначное соответствие между вершиной и ее содержанием, но не всегда наоборот.
Обычно дерево структуры ФС не сбалансировано, т.е. пути на графе структуры от файлов к корню различны по длине. Мы же будем рассматривать более подробно структуру самого содержимого потока (в том числе и файла), и представлять его как разбиение на иерархию информационных элементов различной размерности, начиная от наименьших. Правила разбиения зависят от статистических свойств текста и самих последовательностей символов алфавита различной длины. Примером такого разбиения, основанного на лингвистической метафоре, является представление текста состоящего из слогов, корней слов, слов, словосочетаний, фраз, абзацев и т.п. Рассматриваемая структура имеет вид сбалансированного центрального дерева [10, 11], у которого все пути от листа к корню одинаковы. Кроме того, мы всегда будем учитывать порядок вхождения элементов на каждом уровне структуры.
Пример
структуры потока
I в виде такого
дерева T = (S,U)
приведен на рис.
2. Дерево представлено
в виде многодольного
графа с корнем
в
узле sN1,
с множеством долей
(или слоев, уровней)
S={S0
, S1,
S2, S3,
… , SN-1,
SN},
каждая доля содержит
упорядоченное
множество вершин
или узлов Sn
= {snk}.
Аналогом файлов
здесь могут быть
некоторые вершины
в долях от
S1 до
SN-1.

Рис 2. Древовидная структура.
Каждой вершине дерева snj, (n < N), а также единственной дуге от нее вверх, поставлено в соответствие ее информационное содержание I(snj), а каждому слою - содержание исходного потока I. Существование такого графа тоже очевидно.
Чем выше уровень положения элемента в иерархии, тем больше его информационное содержание. Таким образом, за одно обращение к такому элементу доступно больше минимальных информационных единиц, чем в линейной структуре. В этом проявляется одно из существенных преимуществ иерархической модели организации хранения и доступа данных по сравнению с линейной. Однако, это преимущество получается за счет наличия избыточности по содержанию, гораздо большего числа узлов и наличию связей между ними.
Фрагмент и его свойства
Фрагментом F Н I называется непустая, произвольная непрерывная подстрока в I, (см. рис 3). На практике мы с ним встречаемся, например, в виде фразы на некотором языке, сообщения при передаче данных, запроса на доступ при поиске и т.п.
Любой фрагмент F можно разложить на составляющие его непересекающиеся смежные части Iµ(snj). А его отображение в T можно представить в виде упорядоченного леса {Tμ(F)} смежных компонент (максимальных по высоте, т.е. по номерам уровней их корневых вершин) с минимальным числом этих компонент равным λ. Фрагменту равно упорядоченное объединение информационных содержаний этих компонент
Иμ О λ I(Tμ(F)) = F
На рис.3 эти максимальные по высоте вершины компонент выделены пунктиром и заполнены серым цветом. Другими словами, однозначное отображение фрагмента на подструктуры типа дерева может определяться несколькими вершинами и существует единственное минимальное число таких деревьев.

В дальнейшем, под отображением F ® {Tλ(F)} НT будем (если это не оговорено особо) понимать именно такой минимальный лес фрагмента.
С другой стороны, всегда существует уровень или доля Sn с минимальным номером n=p, p≤N и такой вершиной spt О Sp в этой доле графа T, при которой выполняется соотношение T(F) Н T(spt). Такое дерево будем называть деревом фрагмента F и, в отличие от других возможных отображений F на T, помечать его звездочкой: T*(F). На рис. 3 такому дереву фрагмента соответствует черная вершина.
Дерево фрагмента T*(F) является наименьшей (по числу компонент) единицей графа, содержащей в себе весь граф T(F) фрагмента и определяющей его локализацию в структуре. Будем говорить, что в этом смысле фрагмент ассоциирован с информационным содержанием своего дерева.
При равенстве фрагмента с информационным содержанием некоторой вершины F=I(spj) эти два определения леса {Tμ(F)} и дерева T*(F) фрагмента эквивалентны.
В потоке I, могут существовать несколько одинаковых по содержанию фрагментов, но их структуры из-за несоответствия разбиений могут различаться. Это несоответствие приводит к нежелательной избыточности и усложнению структуры. Для того чтобы этого различия не было, условимся, что разбиения проводятся таким образом, что любые одинаковые фрагменты имеют отображения на изоморфные [10] древовидные графы. Очевидно, что это условие реализуемо.
3. Иерархически сетевые информационные структуры
Дальнейшим развитием древовидных информационных структур можно считать иерархически сетевую. Она обладает новыми положительными свойствами, одним из важнейших среди них является наличие взаимнооднозначного соответствия между любым узлом (или дугой) графа и его содержимым, т.е. полная ассоциативность всех ее элементов. Покажем существование таких структур и рассмотрим процесс ее получения из древовидной структуры. Для этого введем некоторые необходимые определения и процедуры.
Эквивалентные объекты древовидных структур.
Пусть в дереве T=(S, U) имеем две различные вершины x и y, такие, что для них одновременно выполняются следующие условия:
1) x, y О Sn - вершины принадлежат одному слою;
2) T(x) « T(y) - их поддеревья изоморфны [10];
3) I(x) = I(y) - их информационные содержания равны.
Тогда такие вершины, а также их структуры, T(x) и T(y) будем называть эквивалентными и, соответственно, обозначать x @ y и T(x) @ T(y).
По аналогии с вершинами x, y дуги от них ux и uy вверх к следующему слою в древовидной структуре также будем называть эквивалентными.
Очевидно, что приведенное выше отношение эквивалентности вершин (и дуг) удовлетворяет следующим свойствам.
Рефлексивность: T(x) @ T(x)
Симметричность: если T(x) @ T(y), то T(y) @ T(x).
Транзитивность: если T(x) @ T(y), и T(y) @ T(z), то T(x) @ T(z).
Существование эквивалентных элементов следует из того, что L>>|B| и в I всегда существуют такие элементы (как, например, символы алфавита или слова в тексте), которые встречаются более чем по одному разу.
Введем операцию объединения эквивалентных структур (и обозначим ее символом С) в слое следующим образом. Разобьем произвольный уровень Sn, n № N на непустые подмножества эквивалентных вершин D1, D2, …, Dω, …, Dα О Sn и " Dω ОSn : Dω № Ш.
Пусть Dω={s, t, …, z}, тогда справедливы соотношения T(s) @T(t)@…T(z), и I(s)= I(t)…= I(z). Обозначим множество дуг от слоя Sn из Dω к Sn+1 как Un+1={us, ut, …, uz}. Тогда I(s)=I(us)=I(t)=I(ut)=, …, =I(z)= I(uz).
1) выберем две произвольные вершины из Dω, например, t, s ОDω (рис. 4).
2) единственная дуга ut от t к следующей Sn+1 доле объявляется со стороны доли Sn смежной (инцидентной) вершине s; следовательно, от s к Sn+1 добавляется новая связь или дуга. Дуга ut сменила со стороны Sn инцидентность с t на s, а число дуг к следующему слою от узла увеличилась на единицу. Обозначим теперь ut как ust. Узлу s теперь инцидентны сверху две дуги ut и ust.
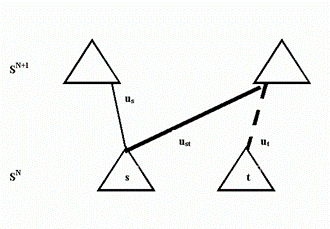
Рис. 4. Объединение эквивалентных узлов;
На рис. 4 это изменение отображено тем, что новая дуга ust выделена более жирной линией, а бывшая ut помечена пунктиром.
В результате смены инцидентности дуги ut узел t теряет связность со следующей долей Sn+1. Поддерево T(t) тоже теряет связность с T и становится компонентой во вновь полученном графе. Граф теряет ацикличность и превращается в сеть
3) Компонента T(t) удаляется из T (на рис. 4 от нее отходит вверх дуга в виде пунктира). Вновь получившееся множество вершин Dω доли Sn уменьшилось на одну вершину t. Обозначим s как dω , а новое множество узлов Sn как Sω.
4) Полученный таким образом новый граф (сеть) помечаем как Cω = (Sω, Uω).
В результате, множество вершин нового графа Cω на n-м уровне равно Sω=Sn\t. Смежности оставшихся вершин графа Cω (т.е. множество дуг U, за исключением добавления новой дуги к s в Uω и удаленной компоненты) остаются прежними.
Смена инцидентности нижнего конца дуги при выполнении операции С не меняет ее информационное содержание.
При выполнении операции С информационное содержание слоя n с учетом числа и связей вниз дуг Uω не изменяется и остается равным потоку I , а поэтому остается в силе и однозначное отображение потока на новую структуру I « Cω=(Dω,Uω). Во вновь полученном графе подграф с уровня n и ниже остается лесом, как и в T(dω) = Т \ T(t).
Информационное содержание каждой вершины и дуги в Cω не изменилось, т.е. для каждой вершины и дуги в T найдется эквивалентная ей в Cω .
Порядок объединения, то есть, какая из двух вершин t или s станет вершиной dω, не влияет на результат операции С (см. перечисленные выше свойства и эквивалентность между элементами графов T и Cω), следовательно, операция С коммутативна относительно своих операндов.
Процедуру последовательного объединения всех элементов в одном подмножестве Dω эквивалентных назовем конденсацией множества Dω. Выполним конденсацию подмножества узлов {s, t, …, z}ОDω . В результате Dω превратится в одноэлементное множество Dω={dω} и ЅDωЅ= 1. Верхняя степень каждого узла dω (число дуг к следующей доле) стала равной числу элементов qω, которое было в эквивалентном ему подмножестве Dω. Связи вышестоящих вершин с нижними удаленными вершинами заменяются на инцидентность к этой единственной подструктуре. (Ближайшим аналогом данной и последующей процедуры является построение в ИПС списочной таблицы с наиболее часто встречаемыми признаками или текстовыми последовательностями, присутствующими в полях БД. Там вместо каждого повторения полного текста в поле записи обычно ставится ссылка на этот элемент таблицы. В итоге появляется возможность сократить общий объем такого ресурса как память, отводимая под таблицы БД [12]).
Конденсацию всех эквивалентных подмножеств в доле назовем конденсацией слоя.
Выполним конденсацию доли n для каждого из подмножеств эквивалентных в ней вершин D1, D2, …, Dω, …, Dα О Sn. Тогда, каждое из перечисленных эквивалентных подмножеств превратится в одноэлементное. В результате получим в слое n множество уникальных вершин Sn ={d1, …, dω,, …, dα}, которое назовем словарем слоя n и обозначим как Dn.
После этого в доле не остается ни одной пары эквивалентных вершин. Получившийся граф определим как Cn=(Dn, Un).
В результате получим следующие свойства графа Cn.
а) Информационное содержание каждого поддерева T(dω), dωОSn не изменилось. Другими словами, каждому узлу dω (и, соответственно, дуге) слоя n в Cn=(Dn, Un), в исходном дереве T=(S,U) соответствует эквивалентное поддерево. Следовательно,
" s О Sn О T $ ! dω О Dn О Cn ® I(s ) = I(dω) (3.1)
" dω О Dn О Cn $ s О Sn О T ® I(dω) = I(s ) (3.2)
" s О Sn О T $ ! dω О Dn О Cn ® T(s ) @ C(dω) (3.3)
б) Структура и информационное содержание каждого элемента подграфа Cn=(Dn, Un) от слоя n+1 и выше не изменились.
Построение графа словарей С.
Выполним конденсацию каждой доли в графе T последовательно сверху от S N-1 вниз до S 0 и получим сетевой граф словарей С=(D, V), D={SN, DN-1, DN-2, …, D0}, в котором SN=DN. При этом аналогично выражениям (3.1) (3.2) и (3.3) будут справедливы следующие соотношения для любого слоя n=[0, 1, 2, …, N-1 ] :
" snm О S n О T $ ! dω О D n ОС ® I(snm ) = I(dω)
" dω О D n ОС $ snm О S nО T ® I(dω) = I(snm )
Или в общем виде:
" snm О T $ ! dn О C ® I(snm ) = I(dn) (3. 4)
" dn О C $ snm О T ® I(dn)= I(snm ) (3. 5)
Очевидно, что при выполнении операции С хотя бы для двух элементов, справедливо условие повторяемости подструктур и
ЅSnЅ > Ѕ DnЅ (3.6)
Отметим, что D0=B, т.е. алфавит в структуре словарей C можно назвать терминальным словарем, а выражения (3.4) и (3.5) для словаря n-й доли аналогичны определению алфавита в (1.1) и (1.2). Условие наличия повторяемости следует из (1.3) и из (3.6).
Таким образом, мы доказали существование отображения дерева на граф словарей T ® С, а, следовательно, и потока на граф словарей I ® C.
Теорема об ассоциативности графа С. Любой фрагмент потока может быть представлен или как дерево T*(F) или как лес смежных компонент {Tμ (F)}, каждой из которых сопоставим некоторый узел (узлы) графа словарей C. В C содержимое узла уникально по построению, поэтому всегда существует взаимнооднозначное соответствие dω«I(dω) между его уникальным идентификатором в структуре и информационным содержанием дерева фрагмента T*(F) или его компонент Tμ (F). Следовательно, структура C=(D, V) полностью ассоциативна по отношению к информационному содержанию ее узлов и вершин.
Следствие. Структура словарей C=(D, V) представляет собой модель ассоциативной памяти.
С позиций лингвистической метафоры, каждый объект структуры C=(D, V) по содержанию является семантическим элементом потока I. В C крупные семантические элементы представляют собой иерархию более мелких и, в то же время, могут содержаться одновременно в нескольких других. Структура C=(D, V) полностью ассоциативна по отношению к семантическим элементам или информационному содержанию ее объектов. В работах [6, 7, 8, 9] функциональная структура такого типа, т.е. структура, в которой узлы наделены определенным набором функций, названа нейросемантической структурой (НСС).
ВЫВОДЫ
1. НСС представляет собой модель, которая обладает свойствами ассоциативной памяти и наиболее близка по свойствам к биологической памяти. Области ее применения в виде среды для хранения и обработки данных практически те же, что и для всех традиционных информационных задач, в том числе и те, где используют нейронные сети [4, 5, 6, 7, 8, 9, 13, 14, 15].
2. Разработанный аппарат позволяет проводить формальный и содержательный анализ потоков и их структур, а также может быть развит далее для решения таких проблем, как, структурная обработка информации, распознавание образов, оптимальное кодирование, лингвистический перевод и т.п. По сравнению с моделями, основанными на нейрокмпьютинге [13, 14, 15], использование моделей на основе НСС делают их более прозрачными и понятными при анализе результата и механизмов работы на идентичных задачах.
3. В НСС подавляющее большинство элементов, имеет иерархию подчиненных и, в то же время, сами они могут подчиняться нескольким (за исключением очень крупных по содержанию единиц самых высоких уровней), а не одному элементу более высокого уровня иерархии. Это хорошо согласуется с информационной моделью мозга. За счет такого "обратного" дерева вверх, появляется возможность строить ассоциативные пути к различным элементам структуры и на их основе конструировать и анализировать модели мехзанизмов обучения и адаптации [16].
4. На количественные параметры и размеры сетевой структуры существенное влияние оказывают статистические свойства элементов потока и качество его разбиения. Реальные потоки данных обладают существенной избыточностью, как по символам алфавита, так и по морфологическим и семантическим единицам (см. выражения 1.3 и 3.6), то есть, имеет место повторяемость не только на уровне алфавита, но и на более высоких. Разбиение должно учитывать эту избыточность, статистику встречаемости и подчиненности символьных подпоследовательностей различной длины. В этом случае вся структура по числу узлов и дуг будет минимальна.
В динамике, при постепенном заполнении НСС данными, на начальной стадии расход ресурса хранения - элементов и их связей - несущественно превышает расход по сравнению с линейной структурой. После накопления элементов-словарей в каждом слое (всех слогов, слов, устойчивых словосочетаний и т.п. элементов), количество новых узлов и связей от уже известных элементов к более высоким в иерархии элементам растет очень медленно, а общий расход ресурса зависит в основном от числа узлов и оценивается как логарифм от объема поступающих данных ЅD n Ѕ » log I.
Следствием
этого является
зависимость времени
доступа по всему
объему потока
(и объема вычислений)
только
от длины фрагмента-запроса,
а не от его произведения
на размер потока,
как это
оценивается в
ИПС. Таким образом,
появляется возможность
на ограниченном
объеме
материального
носителя данных
хранить и обрабатывать
практически неограниченные
объемы реальной
информации в текстовой
форме, а также
эффективно и без
потерь ее
сжимать. Средний
коэффициент компрессии
по числу элементов
структуры можно
представить как
отношение
(ЅD
n
Ѕ) /
log
I.
5. Свойство сжатия потока может быть использовано для повышения пропускной способности каналов связи [17]. С точки зрения классической теории передачи информации, НСС содержит сильно зависимые и, благодаря этому, хорошо прогнозируемые последовательности. Отчего любые крупные фрагменты потока (как элементы из которых состоит сообщение) характеризуются низкой энтропией [18] и могут быть представлены эффективными кодами. Из свойств сжатия потока в графе словарей C=(D, V) следует, что чем больше фрагмент-сообщение, выше может быть его сжатие и, соответственно, эффективнее коды этого сообщения. Кодирование сообщений-фрагментов на основе НСС предлагается называть низкоэнтропийным, как и каналы связи их использующие.
5. Так как операция С существенно уменьшает число связей и узлов за счет удаления дублирующих информацию компонент, то процесс построения графа словарей и его технологические аналоги могут быть полезны при анализе и разработке оптимальных модульных систем обработки данных [19].
6. Перечисленные выше свойства НСС позволяет предположить, что в недалеком будущем на ее основе будут разработаны и найдут широкое применение ассоциативные файловые системы нового поколения, которые позволят организовать ассоциативный доступ не только к отдельным файлам, но и к его частям на всем объеме доступной информации.
Литература
1) Прангишвили И.В., Попова Г.М., Смородинова О.Г., Чудин А.А., - Однородные микроэлектронные ассоциативные процессоры, под ред. И.В. Прангишвили, М., «Сов. Радио», 1973, 280 с.
2) Кохонен Т., Ассоциативная память, пер. с англ., М., Мир, 1980, 239 с.
3) Кохонен Т., Ассоциативные запоминающие устройства:, пер. с англ., М., Мир, 1982, 384 с.
4) Радченко А. Н. Ассоциативная память. Нейронные сети. Оптимизация нейропроцессоров., СПб.: Наука, 1998, 261 с.
5) Огнев И.В., Борисов В.В. – Интеллектуальные системы ассоциативной памяти. – М.: Радио и связь, 1996, 176 с.
6) Бодякин В.И. Информационные иерархически-сетевые структуры для представления знаний в информационных системах. //Проблемно-ориентированные программы. Модели, интерфейс, обучение: Сб. трудов. – М.: Институт проблем управления, 1990.
7) Бодякин В.И. Нейролингвистическая форма представления информации на нейроноподобных элементах, - тезисы семинара-совещания «Алгоритмы обработки информации в нейроноподобных системах», г. Н-Новгород, 14-16 сентября 1993г.
8) Бодякин В.И., Куда идешь, человек? (Основы эволюциологии. Информационный подход). - М. СИНТЕГ, 1998, 332с.
9) Бодякин В.И., Чистяков А.А., Развитие систем хранения данных и архитектура памяти на основе нейросемантических структур, - в сб. Проблемы информатики - материалы III научной конференции "От истории природы к истории общества: "Прошлое в настоящем и будущем", М., 2001.
10) Зыков А.А., Основы теории графов. - М., Наука, 1987, - 384 с.
11) Новиков Ф.А. Дискретная математика для программистов. - СПб.: Питер, 2002.-304 с.: ил.
12) Дж. Мартин, Организация баз данных в вычислительных системах, Мир, 1980, 662 с.
13) Уоссермен Ф. Нейрокомпьютерная техника, теория и практика, под ред. А. И. Галушкина, М., Мир, 1992, 238с.
14) Галушкин А.И. - Сфера применения нейрокомпьютеров расширяется – приложение к журналу «Информационные технологии» № 10/2001.
15) Галушкин А.И. Нейрокомпьютеры, М., ИПРЖР, 2000, 528 с.
16) Умрюхин Е.А. Механизмы мозга: информационная модель и оптимизация обучения, - М. 1999, - 96 с.
17) Чистяков А.А. Эволюция систем обмена данными - в сб. Проблемы информатики - материалы III научной конференции "От истории природы к истории общества: "Прошлое в настоящем и будущем", М., 2001.
18) Shannon C., A mathematical theory of communication, Bell System Techn. J., 27 (1948), № 3, 379-423; 28 (1948) , № 4, 623-656.
19) Косяченко С.А., Товмасян А.В., Чистяков А.А., Островский Б.А. Методы анализа при разработке типовых модульных систем обработки данных. – В кн.: Анализ и синтез оптимальных модульных систем обработки данных. – М., Институт проблем управления, 1984.
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



