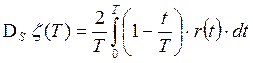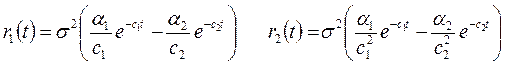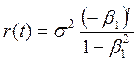научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 03, март 2012
УДК 519.24
МГТУ им. Н.Э. Баумана
Московский автомобильно-дорожный государственный технический университет (МАДИ)
ВВЕДЕНИЕ
Статистический анализ временного ряда, сгенерированного имитационной моделью в целях получения оценок характеристик функционирования системы, является неотъемлемой частью имитационного моделирования. При разработке имитационных экспериментов и анализе результатов моделирования приходится сталкиваться с рядом проблем, важнейшие из которых следующие:
· необходимость учета коррелированности данных выходного процесса имитации;
· проведение анализа влияния начальных условий моделирования;
· необходимость учета переходного процесса на начальном этапе моделирования;
· выбор интервала моделирования;
· определение стратегии моделирования.
В данной работе предполагается, что производится моделирование исходно стационарных процессов. Нестационарность проявляется только за счет выбора начальных условий моделирования. Будем называть такой процесс условно нестационарным. При этом важнейшими характеристиками процесса, влияющими на оценку его математического ожидания, является автоковариационная функция и тренд.
В дальнейшем будем предполагать, что выходной процесс имитации представляет собой стационарный эргодический процесс ξ(t) и, в первую очередь, оценивается математическое ожидание установившегося режима в виде
| (1) |
ЭКСПЕРИМЕНТАЛЬНЫЙ АНАЛИЗ АВТОКОВАРИАЦИОННОЙ ФУНКЦИИ
Проведен анализ вида автоковариационных функций (АКФ) для широкого спектра имитационных моделей. На рис. 1, 2 и 3 представлены структуры некоторых моделей и их автокорреляционные функции, полученные в результате имитационного моделирования.
В качестве объекта имитации рассматривались разомкнутые и замкнутые системы и сети массового обслуживания с различными значениями характеристик входных потоков, времен обслуживания и др.
При идентификации моделей примем следующие обозначения:
A -среднее значение интервала поступления требований;
B - среднее время обслуживания;
V - среднее время пребывания;
Ltr - длина тренда реализации имитационной модели;
Ntr - количество реализаций для построения тренда;
N - число узлов сети массового обслуживания (СеМО);
r - АКФ;
Ter - населенность СеМО.
|
|
а) структура модели | б) автокорреляционная функция r(t) |
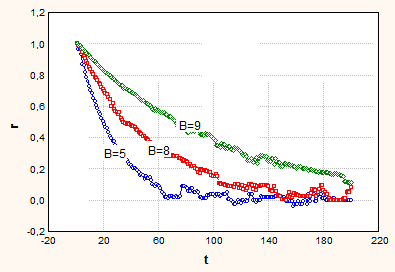
Рис. 1. Однофазная разомкнутая СеМО. А=10, Ltr=5000
Из графиков видно, что чем больше значение B, которое определяет загрузку, тем более затянутой является АКФ.
|
|
а) структура модели | б) автокорреляционная функция r(t) |
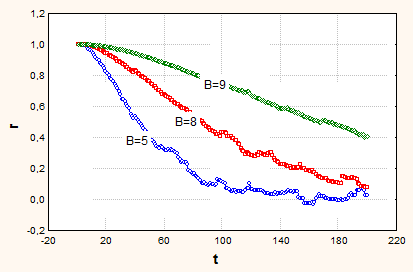
Рис. 2. Разомкнутая трехфазная СеМО. А=10, Ltr=5000
На графиках рис.2 видна аналогичная тенденция к затягиванию процесса (свойство инерционности) при возрастании загрузки. Однако при этом меняется и характер автокорреляционной функции. Если в однофазной СМО АКФ была вогнутой на всем интервале, то в данном случае на начальном интервале она выпукла.
|
|
а) структура модели | б) автокорреляционная функция r(t) |
Рис. 3. Замкнутая однофазная СеМО. A=5, B=10
В замкнутых системах наблюдается несколько иной характер автокорреляции, однако, и здесь видны ее апериодические свойства.
АНАЛИТИЧЕСКИЕ МОДЕЛИ АКФ
В ряде работ предлагается аппроксимировать автокорреляционную функцию экспонентой:
r(τ)=σ2e-c|t|, | (2) |
где σ - среднеквадратическое отклонение процесса.
Так, для гауссовского марковского стационарного случайного процесса автокорреляция имеет вид σ2r-|τ|, где 0<r<1. Поэтому для процесса с экспоненциальной автокорреляцией при построении условных распределений можно учитывать лишь последнее состояние процесса в момент t0.
Однако, как видно из вышеприведенных графиков, автокорреляционная функция в ряде случаев имеет тенденцию к «затягиванию» в начале координат, и, соответственно, к более медленному затуханию. Поэтому предлагается автоковариационную функцию аппроксимировать зависимостью
| (3) |
где c1>0 и c2>0 параметры автоковариации, а α1 и α2 - некоторые функции параметров c1 и c2. Зависимость (3) включает экспоненциальную, как частный случай.
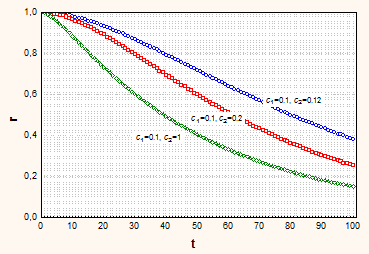
Варьируя указанные параметры, можно моделировать достаточно широкий класс автокорреляций. На рис. 4 приведены графики автокорреляционных функций, полученных при различных комбинациях значений параметров с1 и с2.
|
|
а) значение с1=0.1 | б) значение с1=0.3 |
Рис. 4. Аппроксимация АКФ
В результате проведенного анализа можно сделать следующие выводы:
· минимум из параметров с1 и с2 определяет длину интервала, на котором корреляция существенна;
· разность между параметрами с1 и с2 определяет вид АКФ при малых значения t. Чем меньше разность, тем более пологая автоковариация в начале.
Как видно из графиков, варьируя параметры c1 и c2, можно добиться большого разнообразия в поведении функции. Для параметров автоковариации введем обозначение Cv=(с1, c2).
Назовем автоковариацию:
без запаздывания - если |с1-c2| велико;
с запаздыванием - если | с1-c2| мало.
Будем называть процесс сильнокоррелированным, если значение min(с1,c2) мало (<0.2), и слабокоррелированным, если значение min(с1,c2) велико (>0.5).
ДИСПЕРСИЯ СРЕДНЕИНТЕГРАЛЬНОЙ ОЦЕНКИ
При известной автокорреляционной функции дисперсия среднеинтегральной оценки математического ожидания стационарного процесса вычисляется на основании
| (4) |
В силу симметричности подынтегрального выражения
| (5) |
Введем обозначения
| (6) |
Тогда дисперсия оценки примет вид
| (7) |
Функции r1(t) и r2(t) далее используются для представления аналитических выражений характеристик процессов.
Для указанных коэффициентов автоковариации графики дисперсии приведены на рис. 5.

Рис. 5. Дисперсия среднеинтегральной оценки стационарного процесса
На графиках видно, что у сильнокоррелированного процесса дисперсия убывает более медленно. Задержка автоковариации также увеличивает дисперсию оценки, причем более существенно при малых интервалах моделирования.
ТРЕНДЫ ПЕРЕХОДНЫХ РЕЖИМОВ ИМИТАЦИОННЫХ ПРОЦЕССОВ
Для приведенных выше моделей кроме экспериментов по оцениванию автокорреляционной функции были проведены эксперименты по оцениванию трендов среднего времени пребывания.
|
|
а) Mx(t) (N=1) | б) Mx(t) (N=5) |
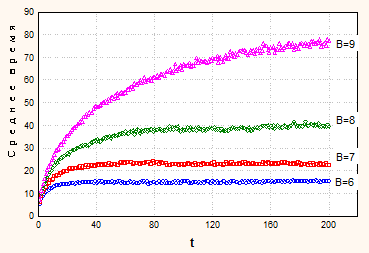
Рис. 6. Тренды средних времен пребывания заявок в разомкнутых СеМО
На рис. 6 приведены графики трендов для однофазной и пятифазной разомкнутой СеМО. Тренды переходных режимов были получены при входном потоке A=10, длине тренда Ltr = 200, количестве реализаций Ntr = 400, и параметрах обслуживания B = {6, 7, 8, 9}.
На графиках виден монотонный характер трендов, причем для однофазной СМО выход в стационарный режим происходит значительно быстрее.
Кроме трендов по среднему времени пребывания были построены тренды среднего квадратического отклонения (СКО) времени пребывания, графики которых приведены на рис. 7.
|
|
а) Sx(t) (N=1) | б) Sx(t) (N=5) |
Рис. 7. СКО разомкнутых СеМО
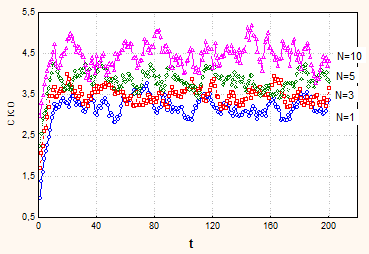
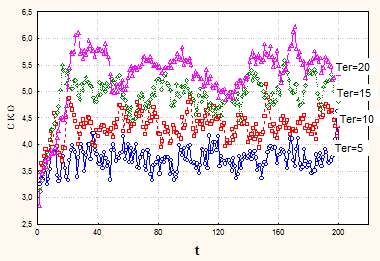
Для замкнутых СеМО графики трендов переходных режимов приведены на рис. 8. В первом случае (8.а) варьировалось число фаз при фиксированной населенности (Ter = 10). Во втором случае (8.б) варьировалась населенность при фиксированном числе фаз (N = 10).
|
|
а) вариация количества фаз | б) вариация населенности |
Рис. 8. Тренды замкнутых СеМО
Как видно из графиков, в начальный период (приблизительно до значения населенности) тренд быстро возрастает, а затем монотонно убывает.
Тренды СКО времени пребывания соответствующих моделей приведены на рис. 9.
|
|
а) вариация количества фаз | б) вариация населенности |
Рис. 9. СКО замкнутых СеМО
Анализ графиков говорит о типе трендов выходных имитационных процессов. Сравнивая поведение автокорреляционных функций и трендов, можно заметить некоторое подобие форм. Если автокорреляция ведет себя более полого, то и тренд более пологий.
МОДЕЛЬ АВТОРЕГРЕССИИ
Предполагается, что имитационные модели будут включены в контур оптимизационных алгоритмов и определены условия сходимости поисковых алгоритмов для процессов, порожденных имитационными моделями. Однако исследование самих алгоритмов оптимизации и поиска, определение наилучшего из них, оценка параметров этих алгоритмов требует генерации большого количества выходных процессов имитации. Известно, что генерация таких процессов с помощью имитационных моделей достаточна трудоемка и требует больших затрат машинного времени.
В данной работе предлагается использовать в качестве выходных процессов имитации случайные процессы, сгенерированные моделями авторегрессии.
О последовательности случайных величин ξ1, ξ2... говорят, что она удовлетворяет стохастическому разностному уравнению (процессу авторегрессии), если существует такая линейная комбинация
| (8) |
что последовательность εp+1, εp+2, ... является последовательностью независимых и одинаково распределенных случайных величин (далее будем полагать Mεt=0).
Наиболее простым случаем является уравнение первого порядка
| (9) |
Автокорреляционная функция такого процесса равна
| (10) |
Учитывая то, что процесс авторегрессии 1-го порядка не отражает особенностей поведения нестационарных выходных имитационных процессов, в частности, не позволяет реализовать «затянутость» АКФ, выполним анализ процесса авторегресси второго порядка
| (11) |
Для вычисления автокорреляционной функции необходимо определить параметрическую систему уравнений относительно неизвестных параметров функции. Для процессов авторегрессии второго порядка эта система разрешима аналитически. В случае действительных и различных корней характеристического уравнения автоковариационная функция имеет вид
| (12) |
где 0<x1<1 и 0<x2<1.
Зависимость (12) приводится к (3) путем замены переменных. Действительно, пусть x1=![]() , x2=
, x2=![]() . Тогда, учитывая условие нормирования, после преобразований получим
. Тогда, учитывая условие нормирования, после преобразований получим
| (13) |
Таким образом, автоковариационная функция процессов авторегрессии принадлежит тому же классу, что и автоковариационная функция выходных процессов имитации.
Рассмотрим характер тренда процесса авторегрессии, начиная с нулевого момента времени. Изменение начальных условий моделирования, приводящих к видоизменению начального участка тренда в процессах авторегрессии, будем имитировать путем задания различных начальных условий. Как показывает анализ, характер поведения трендов процессов авторегрессии близок к выходным имитационным процессам.
ЗАКЛЮЧЕНИЕ
Таким образом, можно сделать следующий вывод: характер автоковариационных функций и тренда типовых выходных процессов имитации и соответствующие характеристики процессов авторегрессии близки друг к другу. Это позволяет при исследовании поисковых алгоритмов оптимизации на имитационных моделей генерировать временные ряды с помощью авторегрессии, заменяя ими громоздкие имитационные модели.
С целью определения класса функций выходных процессов имитации проведено имитационное моделирование типовых структур СеМО, а именно, разомкнутые одно- и многофазные СМО с различными дисциплинами обслуживания, и замкнутые одно- и многофазные СМО с источниками различной населенности и дисциплинами обслуживания. При этом анализировался характер поведения тренда и вид автокорреляционной функции. В результате показано, что автокорреляционная функция имеет апериодический характер и, в случае многофазных СМО, «затянута» в начале координат (имеет точку изгиба).
Вследствие влияния начальных условий моделирования тренд имеет характер апериодической функции, асимптотически сходящейся к некоторому стационарному значению. Проведена классификация трендов на инерционные, безинерционные, монотонные, с запаздыванием и без запаздывания.
Для предложенной автокорреляционной функции стационарного выходного процесса получено аналитическое выражение дисперсии среднеинтегральной оценки. Показано, что на дисперсию оказывают существенное влияние параметры автокорреляционной функции, а также степень ее «затянутости».
Библиографический список
1. Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерные приложения. – М.: Издательский центр Академия, 2003.–432 с.
2. Гнеденко Б.В., Коваленко И.Н. Введение в теорию массового обслуживания. – М.: Издательство ЛКИ, 2007. – 400 с.
3. Кельтон В., Лоу А. Имитационное моделирование. – СПб.: Питер, 2004. – 847 с.
Публикации с ключевыми словами: имитация, тренд, автокорреляция, системы массового обслуживания
Публикации со словами: имитация, тренд, автокорреляция, системы массового обслуживания
Смотри также:
- 77-30569/359132 Влияние начальных условий и длительности моделирования на характеристики условно-нестационарных процессов.
- 77-30569/292475 Объектно-ориентированное описание предметной области при моделировании процессов ликвидации последствий аварийных разливов нефти
- 77-30569/292147 Алгоритмы генерации процесса имитации
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||
 .
.