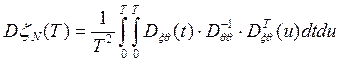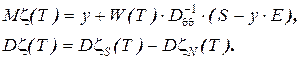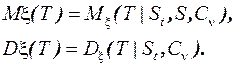научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 04, апрель 2012
УДК 519.24
МГТУ им. Н.Э. Баумана
Московский автомобильно-дорожный государственный технический университет (МАДИ)
ВВЕДЕНИЕ
Для анализа влияния начальных условий на выходной имитационный процесс [2] и разработки стратегии моделирования необходима аналитически разрешимая модель. В качестве основы такой модели в статье предлагается использовать гауссовские процессы. Пусть ξ(t) - гауссовский стационарный процесс (процесс называется гауссовским, если все его конечномерные распределения гауссовские). Если зафиксировать начальные значения процесса, то получим условно нестационарный процесс. Автоковариационную функцию будем аппроксимировать зависимостью
| (1) |
где c1>0 и c2>0 параметры автоковариации, а α1 и α2 - некоторые функции параметров c1 и c2. Для параметров автоковариации будем использовать обозначение Cv=(с1, c2). При этом процесс будет сильнокоррелированным, если min(с1,c2) - мал (<0.2) и слабокоррелированным, если min(с1,c2) - велик (>0.5).
ХАРАКТЕРИСТИКИ УСЛОВНО НЕСТАЦИОНАРНОГО ПРОЦЕССА
Пусть вектор-столбец S=(S0, S-1, ... , S-m)T определяет значения основного процесса ξ(t) в моменты St=<t0,t-1,…,t-m> , (t0 > t-1 > ... > t-m). Обозначим фрагмент случайного процесса, определенный в моменты Stчерез θ. Этот вектор является числовой выборкой из пространства состояний, и при анализе основного процесса представляет выборку из (m+1)-мерной случайной величины, определяющей глубину предыстории. Будем считать, что процесс начинается с момента времени t1.
На основании теоремы о нормальной корреляции [1] получим выражение для математического ожидания условно нестационарного процесса с заданной предысторией
| (2) |
где y - математическое ожидание стационарного процесса;
E – вектор-столбец единиц размерностью (m+1).
Ковариационная функция процесса определяется следующим выражением
| (3) |
где Dξθ(t) = (r(t-t0), r(t-t-1), ... , r(t-t-m), вектор- строка ковариаций;
Dθθ=||cov(ξ(ti), ξ(tj))|| = ||r(ti-tj)||, i,j=0,-1, …, -m, матрица ковариаций предыстории процесса в моменты ti, tj;
r(t) - автокорреляционная функция стационарного процесса.
На рис. 1 и 2 приведены графики дисперсии и математического ожидания для введенной автокорреляционной функции r(t) в зависимости от начальных условий моделирования St и коррелированности стационарного процесса Cv.
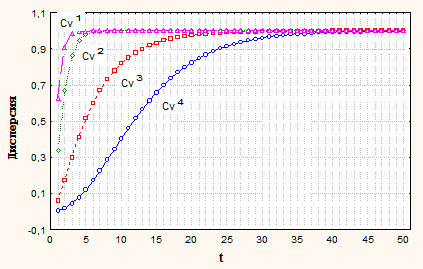
Рис. 1. Дисперсия условно нестационарного процесса
Здесь: Cv1=(1, 2), Cv2=(0.3, 1), Cv3=(0.2, 0.3), Cv4=(0.1, 0.2) ;σ=1.
Дисперсия условно нестационарного процесса не зависит от начального состояния и определяется только коррелированностью. Из графиков видно, что для коррелированных процессов дисперсия существенно медленнее сходится к стационарному значению.
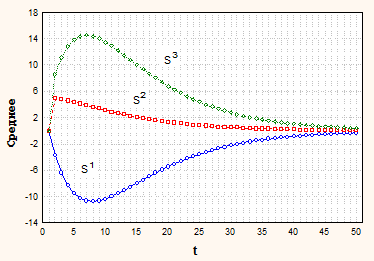
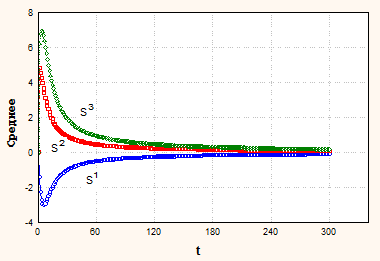
На рис. 2 приведены тренды математического ожидания условно нестационарных процессов.
|
|
а) Cv1 | б) Cv2 |
Рис. 2. Тренды МО условно нестационарных процессов
Здесь: Cv1=(0.2, 0.1), Cv2=(0.4, 0.3); начальные условия St=(0, -1), S1=(5,0), S2=(5,5), S3=(0,5).
Как видно из графиков, начальное состояние существенно сказывается на поведение тренда. Чем дальше начальное состояние от стационарного, тем более длительно восстановление.
В результате вид трендов МО определяют следующие факторы:
· коррелированность;
· задержка автоковариации;
· близость начальных условий.
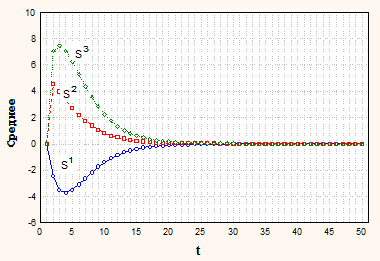
Их влияние схематично отражено на графиках рис. 3.
Сильнокоррелированный процесс | Слабокоррелированный процесс |
|
|
а) близкие начальные условия
|
|
б) далекие начальные условия
Рис. 3. Тренды условно нестационарных гауссовских процессов
На рисунке верхние графики соответствуют трендам без задержки, а нижние с задержкой. В таблице 1 приведена классификация видов трендов в зависимости от исследуемых факторов.
Таблица № 1
Классификация трендов
Ковариация | Коррелированность | Начальное состояние | Процесс |
Без задержки | слабая | близкое | безинерционный |
Без задержки | слабая | далекое | монотонный |
с задержкой | слабая | близкое | монотонный |
с задержкой | слабая | далекое | монотонный с запаздыванием |
без задержки | сильная | близкое | монотонный с запаздыванием |
без задержки | сильная | далекое | монотонный с запаздыванием |
с задержкой | сильная | близкое | монотонный |
с задержкой | сильная | далекое | немонотонный |
ХАРАКТЕРИСТИКИ СРЕДНЕИНТЕГРАЛЬНОЙ ОЦЕНКИ
Среднеинтегральная оценка математического ожидания основного процесса [3] является стохастическим интегралом
| (4) |
и имеет математическое ожидание
| (5) |
Введенные выше обозначения позволяют представить математическое ожидание среднеинтегральной оценки условно нестационарного процесса в виде
| (6) |
Дисперсия оценки вычисляется путем интегрирования ковариационной функции основного процесса по всей области определения
| (7) |
Подставляя в этот интеграл выражение для ковариации и используя правила интегрирования векторных функций получим
| (8) |
Введем следующие обозначения для составляющих интеграла:
стационарная составляющая:
| (9) |
нестационарная составляющая:
| (10) |
При этих обозначениях общая дисперсия будет равна
| (11) |
Двойной интеграл в последнем выражении допускает разделение переменных, поэтому после соответствующих преобразований и перехода к векторной форме, получим
| (12) |
Используя обозначение  , выражение для нестационарной составляющей может быть представлено как
, выражение для нестационарной составляющей может быть представлено как
| (13) |
В результате выражения для математического ожидания и дисперсии среднеинтнгральной оценки можно представить в виде
| (14) |
Проведем анализ полученных соотношений для автокорреляционной функции.
Компонента функционала W примет вид
| (15) |
Используя обозначения
| (16) |
получим
| (17) |
Исследуемыми зависимостями являются математическое ожидание и дисперсия среднеинтегральной оценки как функции от начальных условий и коррелированности процесса:
| (18) |
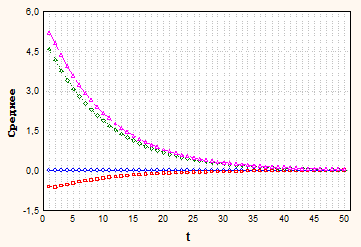
На рис. 4 приведены графики дисперсии среднеинтегральной оценки стационарного (DYS) и условно нестационарного процесса DY для параметров автокорреляционной функции, равных: Cv1=(0.2, 0.1), Cv2=(0.3, 0.2), Cv3=(0.4, 0.3). Дисперсия среднеинтегральной оценки процесса определяется только коррелированностью и не зависит от начальных условий моделирования.
Таким образом, для дисперсии условно нестационарного процесса характерно немонотонное поведение. На начальном этапе дисперсия мала, что объясняется небольшими изменениями значений процесса на коротком периоде времени. Затем дисперсия растет, но наступает момент времени, когда эргодические свойства процесса начинают преобладать и дисперсия стремится к нулю.
|
|
а) DYS | б) DY |
Рис. 4. Дисперсия среднеинтегральной оценки
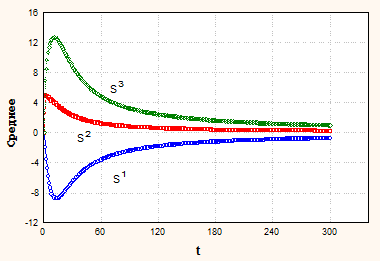
Тренды среднего значения, кроме коррелированности, зависят также от начальных условий процесса. На рис. 5 приведены графики математических ожиданий среднеинтегральной оценки условно нестационарных процессов. При построении трендов варьировались как параметры коррелированности, так и начальные условия Sj. В качестве начальных условий были выбраны St=(0, -1); S1=(5,0), S2=(5,5), S3=(0,5).
|
|
а) Cv=(0.3, 0.4) | б) Cv=(0.1, 0.2) |
Рис. 5. Математическое ожидание среднеинтегральной оценки
Из сравнения графиков среднеинтегральной оценки и основного процесса можно заключить, что тренды среднеинтегральной оценки существенно более затянуты. Так, если для основного процесса характеристики были близки с стационару уже при t=20, то для среднеинтегральной оценки период восстановления математического ожидания достигал значения 200.
ЗАКЛЮЧЕНИЕ
Для целей аналитического исследования сходимости процессов имитационного моделирования предложен условно нестационарный гауссовский процесс, который рассматривается как стационарный гауссовский процесс с заданной предысторией в моменты времени, меньшие нуля, и введенной выше автокорреляционной функцией.
Получены выражения для дисперсии и тренда условно нестационарного процесса в зависимости от параметров автокоррелляционной функции, начальных условий. Показано, что возможно описание в этом классе различного вида монотонных трендов, а, при сильной автокорреляции и далеких начальных условиях, возможно описание и немонотонного тренда. Показано, что характер дисперсии соответствует экспериментальным данным и не зависит от начальных значений.
Получены аналитические выражения тренда и дисперсии среднеинтегральной оценки. Проведено исследование зависимости среднеинтегральной оценки от различных факторов. Показано, что тренд среднеинтегральной оценки имеет затянутый характер, содержит существенную систематическую погрешность на начальном этапе, зависит от коррелированности процесса, начальных значений, длительности моделирования. Показано, что дисперсия среднеинтегральной оценки имеет унимодальный характер с максимумом на начальном этапе моделирования и не зависит от начальных значений процесса.
Библиографический список
1. Волков И.К., Зуев С.М., Цветкова Г.М. Случайные процессы. – М.: Издательство МГТУ им. Н.Э. Баумана, 2001. – 448 с.
2. Кельтон В., Лоу А. Имитационное моделирование. – СПб.: Питер, 2004. – 847 с.
3. Кобзарь А.И. Прикладная математическая статистика. Для инженеров и научных работников. – М.: ФИЗМАТЛИТ, 2006. – 816 с.
Публикации с ключевыми словами: статистические оценки, имитация, гауссовские процессы, нестационарные процессы
Публикации со словами: статистические оценки, имитация, гауссовские процессы, нестационарные процессы
Смотри также:
- Оценка параметра степенной модели Лемана-Кокса методом минимизации функционалов типа Колмогорова-Смирнова и Сэвиджа
- 77-30569/292475 Объектно-ориентированное описание предметной области при моделировании процессов ликвидации последствий аварийных разливов нефти
- 77-30569/292147 Алгоритмы генерации процесса имитации
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||