научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 04, апрель 2012
УДК519.3
МГТУ им. Н.Э. Баумана
Введение
Увеличение надёжности и долговечности ответственных элементов конструкций, работающих в условиях сложного термомеханического нагружения, является одной из приоритетных задач современного машиностроения.
Оценке надёжности и долговечности предшествует анализ напряжённо-деформированного состояния исследуемых элементов конструкций с учетом особенностей контактного взаимодействия. А так как контакт – это основной метод приложения нагрузок к деформируемому телу и, учитывая, что концентрация напряжений в зоне контакта часто вызывает разрушение материала, то решение контактных задач является весьма актуальным. Аналитические решения могут быть получены только для очень ограниченного класса контактных задач, поэтому необходимо развивать численные методы их решения. С этой точки зрения важным является дальнейшее развитие перспективных прикладных методов математического моделирования применительно к решению контактных задач механики с учетом неупругого деформирования материала исследуемых конструкций. Это даёт возможность проведения более полного и тонкого анализа напряженно-деформированного состояний ответственных элементов конструкций, подверженных сложному термосиловому нагружению, и, таким образом, получения данных для более точной оценки их ресурса.
Актуальной является также проблема создания новых эффективных алгоритмов и на их основе современного прикладного программного обеспечения для решения контактных задач вычислительной механики. В настоящее время для решения контактных задач в рамках конечно-элементной технологии используют алгоритмы, основанные на метод штрафных функций, методе множителей Лагранжа, комбинировании методов штрафных функций и множителей Лагранжа [2, 4], имеются работы, в которых используется понятие "псевдосреды" [1]. В данной работе рассматривается алгоритм решения контактной задачи теории упругопластичности, базирующийся на альтернирующем методе Шварца [9], основанном на раздельном рассмотрении контактирующих тел и принципе поочередности. Этот метод позволяет отказаться от значительной части ограничений, накладываемых на используемые конечно-элементные модели (сетки); не возникает необходимости в переформировании глобальных матриц жесткости при изменении геометрии зон контакта; метод отличается относительно быстрой сходимостью.
1. Математическая постановка контактной задачи теории упругости
Рассмотрим два двухмерных однородных и изотропных линейно-упругих контактирующих тела ![]() и
и ![]() , занимающих на плоскости (в пространстве
, занимающих на плоскости (в пространстве ![]() ) области
) области ![]() и
и ![]() и ограниченных кусочно-гладкими границами
и ограниченных кусочно-гладкими границами ![]() и
и ![]() . Введем на плоскости декартовую систему координат
. Введем на плоскости декартовую систему координат ![]() (рисунок 1).
(рисунок 1).
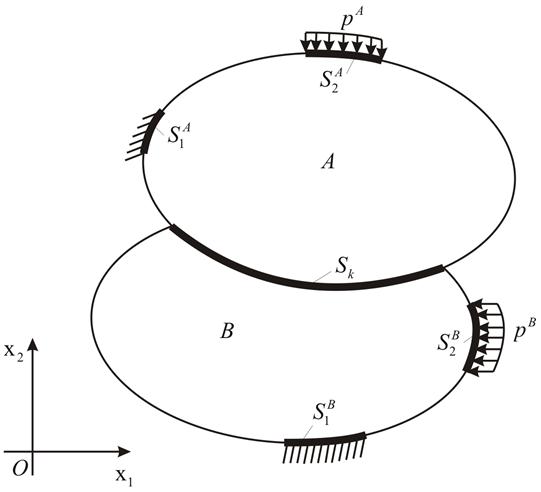
Рисунок 1 - Схема контактного взаимодействия двух тел
Математическая формулировка контактной задачи теории упругости в этом случае будет включать:
уравнения равновесия:
![]() ,
, ![]() ,
, ![]() ;
; ![]() ; (1)
; (1)
граничные условия (кинематические и силовые соответственно):
![]() ,
, ![]() ;
; ![]() ; (2)
; (2)
![]() ,
, ![]() ,
, ![]() ;
;![]() ; (3)
; (3)
соотношения Коши:
 ,
, ![]() ,
, ![]() ;
;![]() ; (4)
; (4)
и определяющие уравнения – закон Гука в виде (начальные напряжения отсутствуют):
![]() ,
, ![]() ,
,![]() , (5)
, (5)
где  – вектор координат,
– вектор координат, ![]() – матрица Гука,
– матрица Гука,  – вектор напряжений,
– вектор напряжений,  – вектор деформации, где
– вектор деформации, где ![]() ,
,  – вектор начальной деформации,
– вектор начальной деформации, ![]() – компоненты массовой (объемной) силы
– компоненты массовой (объемной) силы 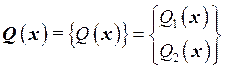 ,
, 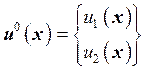 – вектор заданных перемещений точек поверхности
– вектор заданных перемещений точек поверхности ![]() ,
, ![]() – компоненты заданной распределенной нагрузки
– компоненты заданной распределенной нагрузки  на поверхности
на поверхности ![]() .
.
Компоненты матрицы Гука зависят от вида рассматриваемого напряжено-деформированного состояния. Если расчет проводить по схеме плоского напряженного состояния, то матрицу Гука следует записать в виде:
 , (5 а)
, (5 а)
в случае плоского деформированного состояния имеем:
 . (5 б)
. (5 б)
Кроме того, на поверхности контакта ![]() должны быть выполнены условия контактного взаимодействия, т.е. условия сопряжения по перемещениям (кинематическое условие):
должны быть выполнены условия контактного взаимодействия, т.е. условия сопряжения по перемещениям (кинематическое условие):
![]() ,
, ![]() ; (6)
; (6)
и по напряжениям (силовое условие):
![]() ,
, ![]() ; (7)
; (7)
где ![]() ,
,![]() – проекции перемещений граничных точек на внешнюю нормаль к границе тела А;
– проекции перемещений граничных точек на внешнюю нормаль к границе тела А; ![]() – начальное расстояние (зазор) по нормали между граничными точками тел
– начальное расстояние (зазор) по нормали между граничными точками тел ![]() и
и ![]() ;
; ![]() ,
,![]() – компоненты напряжений по внешней нормали к границе тела
– компоненты напряжений по внешней нормали к границе тела ![]() .
.
Совокупность соотношений (1) – (7) составляет математическую формулировку контактной задачи теории упругости. Для ее решения в данной работе был использован алгоритм, основанный на альтернирующем методе Шварца [9].
2. Основные процедуры альтернирующего метода Шварца
Альтернирующий метод Шварца является итерационным методом. Его суть состоит в следующем. На первом шаге на контактных поверхностях тел ![]() и
и ![]() соответственно
соответственно ![]() и
и ![]() задают начальные перемещения
задают начальные перемещения ![]() и
и ![]() , которые имеют смысл дополнительных кинематических условий. Значения компонент векторов
, которые имеют смысл дополнительных кинематических условий. Значения компонент векторов ![]() и
и ![]() выбирают из диапазона ожидаемых значений для зоны контактного взаимодействия.
выбирают из диапазона ожидаемых значений для зоны контактного взаимодействия.
В начале решения контактные поверхности ![]() и
и ![]() могут совпадать (рисунок 2(а)), но могут и не совпадать (рисунок 2(б)). Это зависит от особенности постановки решаемой контактной задачи. В конце решения контактной задачи геометрически скорректированные поверхности контакта совпадают
могут совпадать (рисунок 2(а)), но могут и не совпадать (рисунок 2(б)). Это зависит от особенности постановки решаемой контактной задачи. В конце решения контактной задачи геометрически скорректированные поверхности контакта совпадают ![]() .
.
Далее решают независимо две подобные задачи теории упругости для тел ![]() и
и ![]() . Затем вычисляют поверхностные силы
. Затем вычисляют поверхностные силы ![]() и
и ![]() на контактных поверхностях
на контактных поверхностях ![]() и
и ![]() и их корректируют так, чтобы выполнялись силовые контактные условия (7).
и их корректируют так, чтобы выполнялись силовые контактные условия (7).
На втором шаге на контактных поверхностях ![]() и
и ![]() задают силовые контактные условия, в качестве которых используют скорректированные поверхностные силы
задают силовые контактные условия, в качестве которых используют скорректированные поверхностные силы ![]() и
и ![]() :
:
![]() ,
, ![]() .
. ![]() ,
,![]() ; (8)
; (8)

Рисунок 2 - Начальная геометрия контактных поверхностей (а – контактные поверхности совпадают, б - контактные поверхности не совпадают)
Далее вновь решают независимо задачи теории упругости отдельно для тел ![]() и
и ![]() . По результатам полученных решений, выполняют коррекцию компонент векторов перемещений
. По результатам полученных решений, выполняют коррекцию компонент векторов перемещений ![]() и
и ![]() соответственно точек контактных поверхностей
соответственно точек контактных поверхностей ![]() и
и ![]() с тем, чтобы не было взаимного проникания контактирующих тел, то есть выполнялись кинематические условия контактного взаимодействия (6). Следует отметить, что коррекция векторов перемещений
с тем, чтобы не было взаимного проникания контактирующих тел, то есть выполнялись кинематические условия контактного взаимодействия (6). Следует отметить, что коррекция векторов перемещений ![]() и
и ![]() влечет геометрическое изменение поверхностей контакта
влечет геометрическое изменение поверхностей контакта ![]() и
и ![]() , например, из рассмотрения исключаются те точки поверхностей контакта
, например, из рассмотрения исключаются те точки поверхностей контакта ![]() и
и ![]() , в которых отсутствуют сжимающие нормальные напряжения.
, в которых отсутствуют сжимающие нормальные напряжения.
Скорректированные перемещения контактных поверхностей ![]() и
и ![]() рассматривают в качестве новых кинематических граничных условий на геометрически измененных поверхностях контакта
рассматривают в качестве новых кинематических граничных условий на геометрически измененных поверхностях контакта ![]() и
и ![]() и вновь решают независимо задачи теории упругости отдельно для тел
и вновь решают независимо задачи теории упругости отдельно для тел ![]() и
и ![]() :
:
![]() ,
, ![]() .
.![]() ; (9)
; (9)
Таким образом, данный алгоритм состоит в реализации итерационного процесса поочередного задания на поверхностях контакта ![]() и
и ![]() векторов перемещений
векторов перемещений ![]() и
и ![]() и векторов поверхностных сил
и векторов поверхностных сил ![]() и
и ![]() , а также в их соответствующей коррекции с тем, чтобы были выполнены либо силовые контактные условия, если в зоне контакта заданы перемещения, либо кинематические, если заданы поверхностные силы. Вопросы сходимости подобного типа алгоритмов рассмотрены в работах [8,9].
, а также в их соответствующей коррекции с тем, чтобы были выполнены либо силовые контактные условия, если в зоне контакта заданы перемещения, либо кинематические, если заданы поверхностные силы. Вопросы сходимости подобного типа алгоритмов рассмотрены в работах [8,9].
Процедуры коррекции векторов перемещений ![]() и
и ![]() и векторов сил
и векторов сил ![]() и
и ![]() рассмотрены ниже в разделе 4.
рассмотрены ниже в разделе 4.
3. Вариационная постановка линеаризованных задач теории упругости и построение СЛАУ
Решение задач теории упругости (1) – (5) , (9) и (1) – (5) , (8) эквивалентно решению соответствующих вариационных задач, т. е. минимизации функционалов полной потенциальной энергии. Рассмотрим постановку вариационных задач, но при этом не будем делать различия между контактирующими телами, то есть индекс ![]() при обозначении тех или иных величин опустим.
при обозначении тех или иных величин опустим.
Выражение функционала полной потенциальной энергии линейно-упругого тела, размещённого в пространстве ![]() и нагруженного массовыми
и нагруженного массовыми ![]() , поверхностными
, поверхностными ![]() и дискретными (сосредоточенными)
и дискретными (сосредоточенными) ![]()
![]() силами, имеет вид [2 – 3]:
силами, имеет вид [2 – 3]:
 , (10)
, (10)
где  – вектор перемещений точек тела;
– вектор перемещений точек тела;  – вектор перемещений фиксированных точек
– вектор перемещений фиксированных точек ![]() тела, в которых заданы дискретные силы
тела, в которых заданы дискретные силы ![]()
![]() ;
; ![]() , если на контактной поверхности
, если на контактной поверхности ![]() заданы перемещения
заданы перемещения ![]() ,
, ![]() , если на контактной поверхности
, если на контактной поверхности ![]() заданы поверхностные силы
заданы поверхностные силы ![]() .
.
Вариационная задача эквивалентная задаче (1) – (5) , (9) имеет вид
 (11)
(11)
Вариационная задача эквивалентная задаче (1) – (5) , (8) может быть записана следующим образом:
 (12)
(12)
Для решения вариационных задач (11) и (12) используем метод конечных элементов.
С учетом закона Гука (5) функционал (10) можно представить следующим образом:
Введем обозначения для интегралов, стоящих в правой части последнего равенства:
 (14)
(14)
Тогда получим в виде:
![]() . (15)
. (15)
Минимизацию функционала (15) выполним с помощью метода конечных элементов. Необходимым условием достижения функционалом (15) экстремума является выполнение условия
 . (16)
. (16)
В (16) глобальный вектор узловых перемещений ![]() состоит из перемещений всех узлов конечно-элементной модели, а так как каждый узел имеет два перемещения, то размерность глобального вектора перемещений равна
состоит из перемещений всех узлов конечно-элементной модели, а так как каждый узел имеет два перемещения, то размерность глобального вектора перемещений равна ![]() , таким образом, имеем
, таким образом, имеем
 , (17)
, (17)
где все перемещения узлов в направлении оси ![]() имеют нечетный индекс, а в направлении оси
имеют нечетный индекс, а в направлении оси ![]() – четный,
– четный, ![]() – общее число узлов конечно-элементной модели рассматриваемого тела.
– общее число узлов конечно-элементной модели рассматриваемого тела.
После выполнения всех конечно-элементных процедур соотношение (16) сводится к матричному уравнению (глобальной системе линейных алгебраических уравнений – СЛАУ), которая имеет вид:
![]() . (18)
. (18)
4. Алгоритм численного решения контактной задачи теории упругости на основе альтернирующего метода Шварца
Рассмотрим подробно работу алгоритма на примере контакта двух тел ![]() и
и ![]() . Пронумеруем узлы контактных поверхностей
. Пронумеруем узлы контактных поверхностей ![]()
![]() , тогда векторы соответственно перемещений контактных узлов
, тогда векторы соответственно перемещений контактных узлов ![]() и узловых сил
и узловых сил ![]() в них можно записать соответственно в виде:
в них можно записать соответственно в виде:
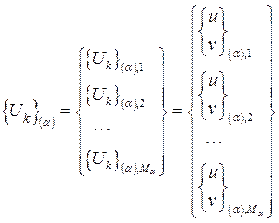 , (19)
, (19)
 , (20)
, (20)
где ![]() – число узлов контактной поверхности
– число узлов контактной поверхности ![]() ,
, ![]() и
и ![]() – компоненты вектора контактных сил в узле
– компоненты вектора контактных сил в узле ![]()
![]() .
.
Последовательно для каждого тела в соответствии с алгоритмом выполняется коррекция компонент векторов ![]() и
и ![]() ,
, ![]() . Коррекция компонент векторов
. Коррекция компонент векторов ![]() и
и ![]() ,
, ![]() реализуется поочередно: на каждой четной итерации корректируются компоненты вектора
реализуется поочередно: на каждой четной итерации корректируются компоненты вектора ![]() , а на нечетной итерации –
, а на нечетной итерации – ![]() .
.
Если начальный зазор отсутствует, то коррекция компонент вектора ![]() выполняется в соответствии с соотношением:
выполняется в соответствии с соотношением:
 (21)
(21)
где ![]() – итерационный параметр,
– итерационный параметр, ![]()
![]() – номер текущего узла, лежащего на контактной поверхности
– номер текущего узла, лежащего на контактной поверхности ![]() тела
тела ![]() , здесь
, здесь ![]() – число контактных узлов на поверхности
– число контактных узлов на поверхности ![]() ;
;  – вектор перемещений сходственной точки
– вектор перемещений сходственной точки ![]() , лежащей на контактной поверхности
, лежащей на контактной поверхности ![]() тела
тела ![]() .
.
Значения компонент ![]() и
и ![]()
![]() в узле
в узле ![]() выбирают из ожидаемого диапазона значений на основании априорной информации о характере контактного взаимодействия.
выбирают из ожидаемого диапазона значений на основании априорной информации о характере контактного взаимодействия.
Для коррекции компонент вектора контактных узловых сил ![]() используется формула:
используется формула:
 (22)
(22)
где ![]() – итерационный параметр,
– итерационный параметр, ![]()
![]() – номер текущего узла, лежащего на контактной поверхности
– номер текущего узла, лежащего на контактной поверхности ![]() тела
тела ![]() ,
,  – вектор контактных узловых сил сходственной точки
– вектор контактных узловых сил сходственной точки ![]() , лежащей на контактной поверхности
, лежащей на контактной поверхности ![]() тела
тела ![]() .
.
Чтобы воспользоваться формулами (21) и (22) необходимо знать компоненты вектора перемещений  и вектора сил
и вектора сил 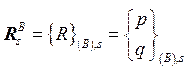 в сходственной точке
в сходственной точке ![]() , лежащей на контактной поверхности
, лежащей на контактной поверхности ![]() тела В. Существуют разные подходы к построению сходственных точек [9], например, в качестве сходственной точки
тела В. Существуют разные подходы к построению сходственных точек [9], например, в качестве сходственной точки ![]() можно использовать точку пересечения перпендикуляра, опущенного из узла
можно использовать точку пересечения перпендикуляра, опущенного из узла ![]() , лежащего на контактной поверхности
, лежащего на контактной поверхности ![]() тела
тела ![]() , на контактную поверхность
, на контактную поверхность ![]() тела
тела ![]() , состоящую из одномерных конечных элементов (граней). При этом точка пересечения должна находиться в пределах соответствующей грани. В данной работе в качестве сходственной точки
, состоящую из одномерных конечных элементов (граней). При этом точка пересечения должна находиться в пределах соответствующей грани. В данной работе в качестве сходственной точки ![]() рассматривалась точка пересечения отрезка
рассматривалась точка пересечения отрезка ![]() , соединяющего начальное
, соединяющего начальное ![]() и конечное
и конечное ![]() положения узла, принадлежащего контактной поверхности
положения узла, принадлежащего контактной поверхности ![]() тела
тела ![]() , с отрезком
, с отрезком ![]() , лежащем на контактной поверхности
, лежащем на контактной поверхности ![]() тела
тела ![]() (рисунок 3).
(рисунок 3).
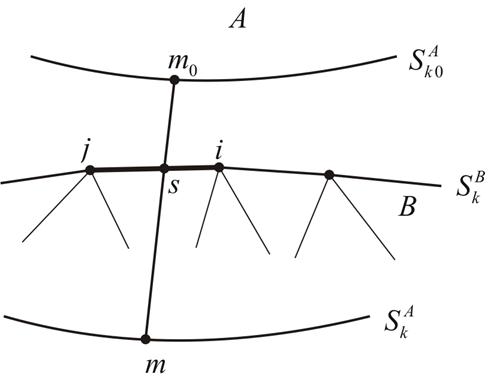
Рисунок 3 - Построение сходственной точки (![]() – начальное положение контактной поверхности тела
– начальное положение контактной поверхности тела ![]() )
)
После того, как сходственная точка ![]() определена, то есть найдены ее глобальные координаты
определена, то есть найдены ее глобальные координаты ![]() и
и ![]() и грань
и грань ![]() контактной поверхности
контактной поверхности ![]() тела
тела ![]() , на которой лежит сходственная точка, на грани
, на которой лежит сходственная точка, на грани ![]() строится внешняя нормаль
строится внешняя нормаль ![]() и вектор касательной
и вектор касательной ![]() к контактной поверхности
к контактной поверхности ![]() тела
тела ![]() (рисунок 4):
(рисунок 4):
 , (23)
, (23)
 , (24)
, (24)
где ![]() – длина отрезка
– длина отрезка ![]() .
.

Рисунок 4 - Построение векторов нормали ![]() и касательной
и касательной ![]() в сходственной точке
в сходственной точке
Затем в узле ![]() вычисляется значение контактной силы
вычисляется значение контактной силы ![]() в направлении внешней нормали
в направлении внешней нормали ![]() , имеем:
, имеем:
![]() , (25)
, (25)
здесь ![]() и
и ![]() – компоненты вектора контактных сил
– компоненты вектора контактных сил  в узле
в узле ![]()
![]() ;
; 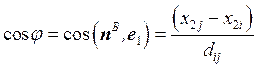 .
.
Далее необходимо проверить выполнение условия:
![]() . (26)
. (26)
Если условие (26) не выполняется, тогда узел ![]() исключатся из описания контактной поверхности
исключатся из описания контактной поверхности ![]() тела
тела ![]() на данной итерации, а при выполнении условия в сходственной точке
на данной итерации, а при выполнении условия в сходственной точке ![]() вычисляются компоненты вектора перемещений
вычисляются компоненты вектора перемещений  (если итерация четная) или вектора сил
(если итерация четная) или вектора сил 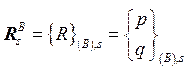 (если итерация нечетная). При этом используются следующие соотношения:
(если итерация нечетная). При этом используются следующие соотношения:
 (27)
(27)
 (28)
(28)
где ![]() и
и ![]() – функции формы одномерного конечного элемента (грани), аппроксимирующего часть контактной поверхности
– функции формы одномерного конечного элемента (грани), аппроксимирующего часть контактной поверхности ![]() тела
тела ![]() (рисунок 4);
(рисунок 4); ![]() ,
, ![]() – длина отрезка
– длина отрезка ![]() ,
, ![]() – длина отрезка
– длина отрезка ![]() .
.
Вычисленные значения компонент вектора перемещений  используются в итерационных соотношениях (21) для коррекции компонент вектора перемещений
используются в итерационных соотношениях (21) для коррекции компонент вектора перемещений 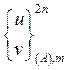 , а компоненты вектора силы
, а компоненты вектора силы 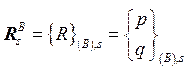 – соответственно в итерационных соотношениях (22) для коррекции компонент вектора силы
– соответственно в итерационных соотношениях (22) для коррекции компонент вектора силы  , узла
, узла ![]() контактной поверхности
контактной поверхности ![]() тела
тела ![]() .
.
Для компонент векторов перемещений и сил узлов контактной поверхности ![]() тела
тела ![]() выполняется совершенно аналогичная процедура коррекции.
выполняется совершенно аналогичная процедура коррекции.
Заметим, что после выполнения коррекции компонент векторов перемещений узлов контактных поверхностей ![]() и
и ![]() , то есть на четных итерациях, узлы контактных поверхностей располагаются на общей контактной поверхности
, то есть на четных итерациях, узлы контактных поверхностей располагаются на общей контактной поверхности ![]() .
.
В том случае, когда имеется первоначальный зазор, соотношение для коррекции компонент перемещений следует использовать в следующем виде:
 (29)
(29)
где ![]() – итерационный параметр;
– итерационный параметр; ![]()
![]() – номер текущего узла, лежащего на контактной поверхности
– номер текущего узла, лежащего на контактной поверхности ![]() тела
тела ![]() , здесь
, здесь ![]() – число контактных узлов на поверхности
– число контактных узлов на поверхности ![]() ;
; ![]() – перемещение узла
– перемещение узла ![]() , лежащего на контактной поверхности
, лежащего на контактной поверхности ![]() тела
тела ![]() , в направлении внешней нормали
, в направлении внешней нормали ![]() к поверхности тела
к поверхности тела ![]() , построенной в сходственной точке
, построенной в сходственной точке ![]() , лежащей на контактной поверхности
, лежащей на контактной поверхности ![]() тела
тела ![]() (рисунок 4);
(рисунок 4); ![]() – перемещение сходственной точки
– перемещение сходственной точки ![]() , лежащей на контактной поверхности
, лежащей на контактной поверхности ![]() тела
тела ![]() , в направлении внешней нормали
, в направлении внешней нормали ![]() к поверхности тела
к поверхности тела ![]() ;
; ![]() – начальный зазор между контактными поверхностями
– начальный зазор между контактными поверхностями ![]() и
и ![]() . Коррекция контактных усилий и в этом случае проводится с помощью соотношения (22).
. Коррекция контактных усилий и в этом случае проводится с помощью соотношения (22).
5. Вычисление итерационных параметров
Для эффективной работы рассмотренного алгоритма важным является вычисление численных значений итерационных параметров ![]() и
и ![]() ,
,![]() ,
, ![]() , здесь
, здесь ![]() – число контактных узлов тела
– число контактных узлов тела ![]() .
.
В работе [8] показано, что итерационные параметры удовлетворяют условиям и между ними существует связь:
![]() (30)
(30)
![]() . (31)
. (31)
Итерационные параметры можно принять постоянными в пределах контактных поверхностей ![]()
![]() и не изменять их значения при проведении итераций, например, положить
и не изменять их значения при проведении итераций, например, положить ![]() . Однако, как показывают многочисленные исследования, такой подход приводит к заметному росту числа итераций. Существенно эффективнее итерационные параметры вычислять отдельно для каждой сопряженной пары узлов
. Однако, как показывают многочисленные исследования, такой подход приводит к заметному росту числа итераций. Существенно эффективнее итерационные параметры вычислять отдельно для каждой сопряженной пары узлов ![]() : узел
: узел ![]()
![]() , рассматриваемой контактной поверхности
, рассматриваемой контактной поверхности ![]()
![]() , и соответствующая ему сходственная точка
, и соответствующая ему сходственная точка ![]() , лежащая на контактной поверхности
, лежащая на контактной поверхности ![]()
![]() ,
, ![]() .
.
В данной работе с учетом результатов численных экспериментов был использован следующий подход. Пусть для определенности ![]() и
и ![]() . На четных итерациях, то есть когда выполняется коррекция компонент вектора перемещения
. На четных итерациях, то есть когда выполняется коррекция компонент вектора перемещения 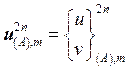 , итерационный параметр
, итерационный параметр ![]() определяется с помощью выражения:
определяется с помощью выражения:
 , (32)
, (32)
где ![]() – норма вектора перемещения
– норма вектора перемещения ![]() узла
узла ![]()
![]() , лежащего на контактной поверхности
, лежащего на контактной поверхности ![]() тела
тела ![]() ,
, ![]() – норма вектора перемещения
– норма вектора перемещения ![]() сходственной точки
сходственной точки ![]() , лежащей на контактной поверхности
, лежащей на контактной поверхности ![]() тела
тела ![]() .
.
Очевидно, что выполняются соотношения:
![]() и
и ![]() . (33)
. (33)
Заметим, что алгоритм вычисления величины ![]() не требует.
не требует.
Соотношение (32) можно записать для компонент вектора перемещения ![]() :
:
 (34)
(34)
где ![]() ,
, ![]() ,
,![]() и
и ![]() – соответственно компоненты векторов перемещений
– соответственно компоненты векторов перемещений ![]() и
и ![]() в направлении внешней нормали
в направлении внешней нормали ![]() и вектора касательной
и вектора касательной ![]() в сходственной точке
в сходственной точке ![]() , лежащей на грани
, лежащей на грани ![]() на контактной поверхности
на контактной поверхности ![]() тела
тела ![]() (рисунок 4)
(рисунок 4)
На нечетных итерациях, то есть когда выполняется коррекция компонент вектора контактных узловых сил ![]() , итерационный параметр
, итерационный параметр ![]() определяется с помощью выражения:
определяется с помощью выражения:
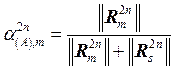 , (35)
, (35)
где ![]() – норма вектора контактных сил
– норма вектора контактных сил ![]() в узле
в узле ![]()
![]() , лежащего на контактной поверхности
, лежащего на контактной поверхности ![]() тела
тела ![]() ,
, ![]() – норма вектора контактных сил
– норма вектора контактных сил ![]() в сходственной точке
в сходственной точке ![]() , лежащей на контактной поверхности
, лежащей на контактной поверхности ![]() тела
тела ![]() .
.
Соотношение (35) можно записать для компонент вектораконтактных сил![]() :
:
 (36)
(36)
где ![]() ,
, ![]() ,
,![]() и
и ![]() – соответственно компоненты векторов контактных сил
– соответственно компоненты векторов контактных сил ![]() и
и ![]() в направлении внешней нормали
в направлении внешней нормали ![]() и вектора касательной
и вектора касательной ![]() в сходственной точке
в сходственной точке ![]() , лежащей на грани
, лежащей на грани ![]() на контактной поверхности
на контактной поверхности ![]() тела
тела ![]() (рисунок 4)
(рисунок 4)
Как показали результаты численных исследований использование для вычислений итерационных коэффициентов ![]() и
и ![]() соотношений (32) и (35) является достаточно эффективным.
соотношений (32) и (35) является достаточно эффективным.
6. Учет трения при решении контактных задач
В данной работе было принято, что трение описывается законом Амонтона–Кулона. Отсюда учет трения между контактирующими поверхностями тел ![]() и
и ![]() (соответственно
(соответственно ![]() и
и ![]() ) требует в каждом контактном узле
) требует в каждом контактном узле ![]() проверки неравенства:
проверки неравенства:
![]() ,
, ![]() ,
, ![]() , (37)
, (37)
где ![]() – коэффициент трения;
– коэффициент трения; ![]() и
и ![]() – компоненты вектора силы
– компоненты вектора силы ![]() в направлении внешней нормали
в направлении внешней нормали ![]() и вектора касательной
и вектора касательной ![]() в сходственной точке
в сходственной точке ![]() , лежащей на грани
, лежащей на грани ![]() на контактной поверхности
на контактной поверхности ![]() тела
тела ![]() ,
, ![]() и
и ![]() (рисунок 5).
(рисунок 5).

Рисунок 5 - Учет сил трения
Векторы нормали ![]() и касательной
и касательной ![]() определяются выражениями:
определяются выражениями:
 , (38)
, (38)
где ![]() – длина отрезка
– длина отрезка ![]() (рисунок 5).
(рисунок 5).
Обозначим через ![]() и
и ![]() компоненты вектора силы и через
компоненты вектора силы и через ![]() и
и ![]() компоненты вектора перемещения в узле
компоненты вектора перемещения в узле ![]() ,
, ![]() ,
, ![]() .
.
Если имеет место строгое неравенство (37), то считаем, что в узле ![]() , например, тела
, например, тела ![]() наблюдается полное сцепление с контактной поверхностью
наблюдается полное сцепление с контактной поверхностью ![]() тела
тела ![]() в сходственной точке
в сходственной точке ![]() . В этом случае следует принять:
. В этом случае следует принять:
![]() , (39)
, (39)
где ![]() – компонента перемещения сходственной точки
– компонента перемещения сходственной точки ![]() , расположенной на контактной поверхности
, расположенной на контактной поверхности ![]() тела
тела ![]() , в направлении вектора касательной
, в направлении вектора касательной ![]() (рисунок 5,
(рисунок 5, ![]() ,
, ![]() ).
).
Нарушение неравенства (37) вызывает взаимное проскальзывание контактирующих тел, поэтому необходимо использовать соотношения, накладывающие ограничения на касательную компоненту силы в узле ![]() ,
, ![]() ,
, ![]() , имеем:
, имеем:
![]() . (40)
. (40)
Таким образом, в начале вычислений с учетом трения все узлы ![]() ,
, ![]() , рассматриваемой контактной поверхности
, рассматриваемой контактной поверхности ![]() ,
, ![]() , считаются сцепленными. С этими граничными (кинематическими) условиями выполняется начальная (нулевая) итерация. После усреднения усилий в зоне контакта проверяется выполнение силового условия (37). В случае невыполнения условия (37) соответствующие узлы переводятся в разряд скользящих и в них ограничиваются касательные усилия по формуле (40). Далее итерационно уточняются компоненты векторов перемещений и сил в контактных узлах по формулам (21) и (22). Практика решения задач показала, что учет трения не увеличивает общего числа контактных итераций.
, считаются сцепленными. С этими граничными (кинематическими) условиями выполняется начальная (нулевая) итерация. После усреднения усилий в зоне контакта проверяется выполнение силового условия (37). В случае невыполнения условия (37) соответствующие узлы переводятся в разряд скользящих и в них ограничиваются касательные усилия по формуле (40). Далее итерационно уточняются компоненты векторов перемещений и сил в контактных узлах по формулам (21) и (22). Практика решения задач показала, что учет трения не увеличивает общего числа контактных итераций.
Также учитывается возможность упругопластического деформирования. Для этого используется метод переменных параметров упругости [7].
7. Анализ результатов численных исследований
На основе разработанного алгоритма был создан комплекс прикладных программ и выполнено его тестирование [10]. Ниже представлены результаты численных исследований, полученные с помощью разработанного комплекса.
Учитывая, что многие ответственные элементы конструкций современного машиностроения наряду с контактным взаимодействием испытывают температурное нагружение, было исследовано контактное взаимодействие двух равномерно нагретых тел, между которыми в естественном (не нагретом) состоянии имеется зазор (рисунок 6).
При расширении тел начальный зазор был полностью выбран. На рисунке 7 представлено поле компоненты ![]() тензора напряжений.
тензора напряжений.
Как видно из рисунка 7, имеет место симметричное распределение напряжений, при этом наибольшие значения получены в зоне непосредственного контакта, а наименьшие на периферии области анализа. Кроме того, повсеместно наблюдается сжатие, кроме зон примыкающих к свободной поверхности, в которых отмечаются сравнительно невысокие по величине растягивающие напряжения.

Рисунок 6 - Расчетная схема контактного взаимодействия равномерно нагретых тел

Рисунок 7 - Поле компоненты ![]() тензора напряжений, МПа.
тензора напряжений, МПа.
Исследовано контактное взаимодействие двух неравномерно нагретых прямоугольных тел (рисунок 8), выполненных из стали 40Х. Размер верхнего тела вдоль оси абсцисс 0.025 м, нижнего – 0.05 м. На верхнее тело действует распределенная горизонтальная нагрузка ![]() . Оба тела подвержены температурному воздействию. В пределах верхнего тела температура меняются от оси закрепления
. Оба тела подвержены температурному воздействию. В пределах верхнего тела температура меняются от оси закрепления ![]() вдоль оси
вдоль оси ![]() до свободной поверхности справа по линейному закону. Максимальное значение температуры равно 600 К и относится к точкам тела, лежащим на оси
до свободной поверхности справа по линейному закону. Максимальное значение температуры равно 600 К и относится к точкам тела, лежащим на оси ![]() , а точки, расположенные на свободной поверхности имеют минимальное значение температуры – 200 К. У точек нижнего тела, для которых
, а точки, расположенные на свободной поверхности имеют минимальное значение температуры – 200 К. У точек нижнего тела, для которых ![]() , аналогичное распределение температуры, а точки, у которых
, аналогичное распределение температуры, а точки, у которых ![]() , имеют постоянную температуру 200 К. Обобщенный график распределения температуры по обоим телам показано на рисунке 9.
, имеют постоянную температуру 200 К. Обобщенный график распределения температуры по обоим телам показано на рисунке 9.

Рисунок 8 - Расчетная схема контактного взаимодействия неравномерно нагретых прямоугольных тел

Рисунок 9 - Распределение температур в контактирующих телах
На рисунке 10 показана геометрия конечно-элементных моделей контактирующих тел после деформирования. Из характера деформирования видно, что температурное воздействие является определяющим. На рисунке 11 приведено поле компоненты ![]() тензора напряжений. Данное поле характеризуется неоднородностью.
тензора напряжений. Данное поле характеризуется неоднородностью.

Рисунок 10 - Геометрия конечно-элементных моделей тел после деформирования
![]()
![]()
![]()
![]()

Рисунок 11 - Поле компоненты ![]() тензора напряжений, МПа.
тензора напряжений, МПа.
Выводы.
Разработан алгоритм решения контактных задач на основе на альтернирующего метода Шварца и создан комплекс прикладных программ. Выполненный цикл численных исследований контактного взаимодействия упругопластических тел, имеющих сложное геометрическое оформление, показал достаточно высокую эффективность разработанного алгоритма и, реализующего его, программного кода.
Список литературы
1. Бабин А.П., Зернин М.В. Конечно-элементное моделирование контактного взаимодействия с использованием положений механики контактной псевдосреды // Механика твердого тела.2009. №4.с. 84-107.
2. Wriggers P., Nour-Omid B. A two-level iteration method for solution of contact problems // Computer methods in applied mechanics and engineering. 1986. №54. pp. 131-144
3. Kikuchi N., Oden J. T. Contact problem in elasticity: a study of variational inequalities and finite element methods. – Philadelphia: SIAM, 1988. 495 p.
4. Wriggers P. Computational contact mechanics. – England: John Wiley & Sons Ltd, 2002 – 441 p.
5. Зенкевич О. Метод конечных элементов в технике — М.: Мир, 1975. -542 с.
6. Шабров Н.Н. Метод конечных элементов в расчетах деталей тепловых двигателей — Л.: Машиностроение, 1983. 213 с.
7. Малинин Н.Н. Прикладная теория пластичности и ползучести — М.: Машиностроение, 1975. 398 с.
8. Цвик Л. Б. Принцип поочередности в задачах о сопряжении и контакте твердых деформируемых тел // Прикладная механика. 1980. т. 16. № 1. с. 13-18.
9. Можаровский Н.С., Качаловская Н.Е. Приложение методов теории пластичности и ползучести к решению инженерных задач машиностроения: В 2 ч. Ч. 2: Методы и алгоритмы решения краевых задач. – К.: Высшая школа, 1991. 287 с.
10. И.В. Станкевич, М.Е. Яковлев, Си Ту Хтет. Разработка алгоритма контактного взаимодействия на основе альтернирующего метода Шварца // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки.- 2011. –Спец. вып. Прикладная математика.- С.134 – 141.
Публикации с ключевыми словами: теория упругости, контактная задача, тензор напряжений, альтернирующий метод Шварца, упругопластичность, итерационный процесс
Публикации со словами: теория упругости, контактная задача, тензор напряжений, альтернирующий метод Шварца, упругопластичность, итерационный процесс
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||




