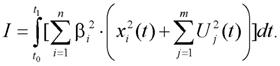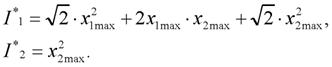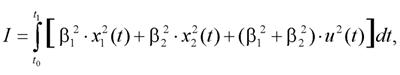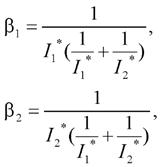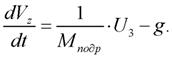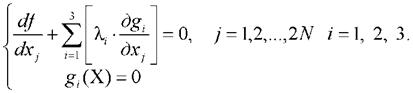научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2011
УДК.62-522.2
МГТУ им. Н.Э. Баумана
Введение
При синтезе системы управления подвеской многоосных колесных машин (МКМ) необходимо разрабатывать алгоритмы управления, обеспечивающие принцип раздельного управления, т.е. работа каждого из алгоритмов управления должна осуществляться в определенном диапазоне изменения фазовых координат системы [1]. Осуществление указанного принципа предполагается следующим образом. При малых углах продольного и поперечного наклона корпуса (до +10о) наиболее актуальным является виброизоляция. Однако при этом управляющий сигнал должен способствовать стабилизации корпуса колесной машины, что обеспечивает не только повышение скорости движения, но и безопасность. При углах наклона корпуса, превышающих указанный предел, наиболее важной становится задача обеспечения его стабилизации, что обеспечивает, во-первых, повышение устойчивости, и, следовательно, безопасности движения, и, во-вторых, улучшаются условия работы водителя, т.к. при больших углах наклона корпуса длиннобазной многоосной машины вождение становится затруднительным.
Внедрение систем управления подвеской МКМ, обеспечивающих перечисленные функции, сдерживается отсутствием законов управления упруго-демпфирующими элементами системы подрессоривания [1].
Теоретические аспекты активных виброзащитных систем для общего случая подрессоривания твердого тела, а также частных случаев, например для подвески сиденья водителя, исследовали многие ученые: Балагула В.Я., Гайцгори М.М., Генкин М.Д., Яблонский В.В., Елисеев С.А, Иносов С.В., Синев А.В., Фурман Ф.А. и др. [2 – 7]. Применительно к автомобилям активное подрессоривание рассматривали в своих работах Кольцов В.И., Фурунжиев Р.И., Останин А.Н., Шарапов В.Д. [8, 9, 10], зарубежные ученые: Саттон X.Б., Томпсон А.Г. и др. [11, 12]. Исследователями отмечается, что наиболее эффективны с точки зрения плавности хода активные подвески.
Целью работы является разработка закона управления подвеской МКМ, обеспечивающего динамическую стабилизацию корпуса при силовом воздействии (при разгоне, торможении, повороте, воздействии импульсной боковой силы).
Задачу оптимального управления можно сформулировать следующим образом [13]:
- даны цель управления, математически представленная в виде некоторого функционала или критерия качества управления;
- уравнения системы (обычно в виде уравнений состояния);
- система граничных условий в начальный и конечный момент времени;
- система ограничений, которым должны удовлетворять переменные состояния и управления.
Требуется найти вектор управления, при котором критерий качества управления имеет экстремум.
1. Синтез закона управления, обеспечивающего стабилизацию
корпуса многоосной колесной машины
Поскольку речь идет о малых углах отклонения корпуса МКМ, то рассмотрим линеаризованную модель его движения относительно только трех фазовых координат (рис. 1):
- относительно вертикальной оси Z связанной с корпусом МКМ системы координат;
- вращение корпуса относительно главной оси инерции Х связанной с корпусом системы координат;
- вращение корпуса относительно главной оси инерции Y связанной с корпусом системы координат;
- вращение корпуса относительно главной оси инерции Y связанной с корпусом системы координат.
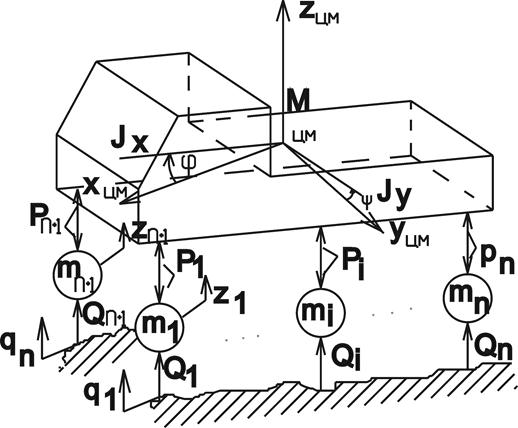
Рис. 1. Расчетная схема многоопорной колебательной системы МКМ
Будем считать корпус абсолютно твердым телом, подвеска колес выполнена по "свечной" схеме [1].
В результате получим следующие упрощенные уравнения движения корпуса многоосной машины
| (1) |
где
U1 - управляющий момент, создаваемый упругодемпфирующими элементами подвески относительно оси Х (приложен к центру масс корпуса многоосного шасси);
U2- управляющий момент, создаваемый упругодемпфирующими элементами подвески относительно оси Y (приложен к центру масс корпуса многоосного шасси);
U3 - управляющий главный вектор сил, создаваемый упругодемпфирующими элементами подвески в вертикальном направлении (приложен к центру масс корпуса многоосного шасси);
ωx – угловая скорость корпуса относительно оси х;
ωy – угловая скорость корпуса относительно оси y;
Vz – скорость корпуса относительно оси z;
φ – угол наклона корпуса относительно оси х;
ψ– угол наклона корпуса относительно оси y;
z – перемещение центра масс относительно оси z;
Jx, Jy – моменты инерции подрессоренной массы МКМ относительно осей x и y соответственно;
Мподр – подрессоренная масса.
В данном случае управление U1 и U2 являются управляющими моментами относительно, соответственно, продольной оси автомобиля Х и поперечной оси Y, проходящей через его центр тяжести. Управление U3 представляет собой управляющий вектор сил, параллельных вертикальной оси Z. Все управляющие воздействия создаются управляемыми упруго-демпфирующими элементами подвески многоосной колесной машины.
Данная система позволяет вырабатывать управляющие воздействия, не только снижающие колебания корпуса колесной машины, но и обеспечивающие его динамическую стабилизацию, что способствует повышению устойчивости движения. Система автоматического управления, описываемая уравнениями (1), может быть разбита на три независимых канала управления: два канала, обеспечивающих гашение угловых колебаний корпуса и его стабилизацию по углу наклона и один канал - по гашению его вертикальных колебаний.
2. Методика синтеза динамического адаптивного непрерывного закона стабилизации корпуса многоосных колесных машин
При синтезе оптимальных систем широко применяют квадратичные интегральные критерии качества, содержащие координаты объекта и управления [14, 15].
Исходная система уравнений состояния (1) представляет собой линейную систему, описываемую векторным дифференциальным уравнением
 (2)
(2)
где X(t) - n-мерный вектор состояния;
A(t), B(t)- матричные функции времени соответственно порядков n×n; n×m;
u(t) - m-мерный вектор управления.
Вектор управления U(t) = [u1(t), …, um(t)]T по понятным физическим причинам является ограниченным, т.е. принадлежащим замкнутому множеству
![]()
Для выбора критерия качества управления сформулируем предъявляемые к нему требования.
Наиболее универсальным является критерий качества, основанный на введении оптимизируемого функционала интегрального типа. Использование интегральных критериев, в частности, квадратичных функционалов, позволяет определить требования к переходным процессам системы управления заданием значений небольшого числа их весовых коэффициентов, практически произвольный выбор которых обеспечивает фундаментальное свойство синтезируемой системы − ее асимптотическую устойчивость [15]. Итерационный целенаправленный перебор весовых коэффициентов, как правило, удовлетворяет разумные требования к первичным показателям качества переходных процессов. Главное достоинство данного способа формализации заключается в том, что он позволяет использовать для синтеза системы управления сложными объектами результаты теории оптимального управления и теории аналитического конструирования оптимальных регуляторов (АКОР) [16]. Все более широкое применение в прикладных задачах управления сложными производственными объектами методов АКОР связано с такими их достоинствами, как общность, предельная формализация, логическая завершенность, принципиальная математическая простота.
Таким образом, для объектов управления (2) приходим к необходимости решения задачи АКОР по соответствующему интегральному критерию. При выборе функционала качества управления (при постановке задачи АКОР) предполагается, что для систем подрессоривания многоосных колесных машин, функционирующих в условиях действия возмущений значительной амплитуды (мощности), желательна стабилизация выходных переменных (скорости, ускорения и перемещения подрессоренных масс) на определенном уровне для улучшения показателей вибронагруженности и устойчивости.
В настоящее время в теории и практике оптимального управления широкое распространение получили интегральные квадратичные обобщенные функционалы качества систем автоматического управления вида [16]:
| (3) |
Значение функционала I зависит от начального состояния X(t0), момента времени t0 и управления U(t) в течение интервала (t0,t1).
Вопрос выбора положительно определенных коэффициентов βi рассмотрен ниже.
В работах [17, 18] n-мерный вектор ![]() рекомендуется определять из условия экстремума одного или нескольких дополнительных критериев качества (γ-критериев), однако при таком подходе к проблеме выбора основного критерия остается определенный произвол в выборе дополнительных критериев.
рекомендуется определять из условия экстремума одного или нескольких дополнительных критериев качества (γ-критериев), однако при таком подходе к проблеме выбора основного критерия остается определенный произвол в выборе дополнительных критериев.
Проблеме выбора критериев оптимальности при конструировании оптимальных регуляторов посвящена также работа М.Е. Салуквадзе [19]. Предложенный в ней метод выбора вектора ![]() основан на идее синтеза парето-оптимального управления, обеспечивающего максимальную близость аддитивного функционала (3) к каждому из функционалов
основан на идее синтеза парето-оптимального управления, обеспечивающего максимальную близость аддитивного функционала (3) к каждому из функционалов
 (4)
(4)
Вместе с тем, метод М.Е. Салуквадзе не предполагает ранжирования критериев (4) по степени их важности.
В работах [20, 21] рассмотрена методика выбора вектора![]() , основанная на требовании быстрейшего убывания функции Ляпунова-Беллмана вдоль траектории замкнутой системы. Действительно, функцию Ляпунова-Беллмана можно трактовать как текущее расстояние между возмущенным состоянием замкнутой системы и невозмущенным состоянием. Динамические свойства системы тем выше, чем быстрее убывает это расстояние в переходном процессе. Вместе с тем, этот метод требует большого объема вычислений в процессе его реализации, а также может приводить к большим значениям коэффициентов усиления оптимального регулятора, соответствующих малым значениям весовых коэффициентов βi, i = 1, …, n.
, основанная на требовании быстрейшего убывания функции Ляпунова-Беллмана вдоль траектории замкнутой системы. Действительно, функцию Ляпунова-Беллмана можно трактовать как текущее расстояние между возмущенным состоянием замкнутой системы и невозмущенным состоянием. Динамические свойства системы тем выше, чем быстрее убывает это расстояние в переходном процессе. Вместе с тем, этот метод требует большого объема вычислений в процессе его реализации, а также может приводить к большим значениям коэффициентов усиления оптимального регулятора, соответствующих малым значениям весовых коэффициентов βi, i = 1, …, n.
Для определения коэффициентов βi, i = 1, …, n воспользуемся методикой, предложенной в работе [22].
Потребуем, чтобы весовые коэффициенты функционала (3) удовлетворяли ограничению
| (5) |
чтобы избежать тривиального решения βi = 0, i = 1, …, n. Тогда задачу АКОР сформулируем в следующем виде: требуется отыскать вектор ![]() , доставляющий на решениях системы (1) минимум функционалу (3) при одновременном отыскании вектора
, доставляющий на решениях системы (1) минимум функционалу (3) при одновременном отыскании вектора ![]() с ограничениями (5). В работе [22] получено выражение для искомых значений компонент вектора βi, i = 1, …, n:
с ограничениями (5). В работе [22] получено выражение для искомых значений компонент вектора βi, i = 1, …, n:
| (6) |
|
Коэффициенты β1 и β2 зависят от максимальных значений x1max и x2max фазовых переменных, что позволяет системе управления адаптироваться к «жесткости» входного воздействия: чем больше величина возмущения, тем больше значение стабилизирующего управляющего воздействия.
3. Разработка законов стабилизации угловых и вертикальных колебаний корпуса многоосной колесной машины
Пусть х1 = φ - угол наклона корпуса; х2 = ω - угловая скорость. Тогда система уравнений, описывающих угловые колебания корпуса МКМ, может быть в виде
| (7) |
В данном случае управление U являются управляющим моментом относительно соответствующей оси автомобиля, проходящей через его центр тяжести. Все управляющие воздействия создаются управляемыми упругодемпфирующими элементами подвески машины.
Требуется найти управление, которое доставляет минимум функционалу
| (8) |
при условии
β1 + β2 = 1.
В работе [22] получено выражение для оптимального управления U
| (9) |
|
Перейдем к построению закона управления, обеспечивающего стабилизацию вертикальных колебаний корпуса. Исходное дифференциальное уравнение имеет вид
| (10) |
Введем новые обозначения. Пусть 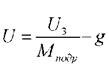 , х1 = z – вертикальное перемещение центра масс корпуса; х2 = Vz – вертикальная скорость центра масс корпуса. Тогда уравнение (10) можно переписать в виде
, х1 = z – вертикальное перемещение центра масс корпуса; х2 = Vz – вертикальная скорость центра масс корпуса. Тогда уравнение (10) можно переписать в виде

Повторив выкладки, приведенные ранее, получим выражение для оптимального управления
| (11) |
4. Методика определения приращения усилий в упруго-демпфирующих элементах подвески, реализующих управляющие воздействия на корпус многоосной колесной машины
При разработке методики примем сквозную нумерацию колес автомобиля:

Понятно, что управляющие силовые факторы Mux = U1, Muy = U2, Rzu= U3 могут быть реализованы только в виде приращения усилия ![]() Pi, i = 1, 2, ... , 2N(где N - число осей колесной машины) в каждом упругодемпфирующем элементе подвески. При этом
Pi, i = 1, 2, ... , 2N(где N - число осей колесной машины) в каждом упругодемпфирующем элементе подвески. При этом
∆Pi=Piд - Pi.
где Piд - действительное текущее значение усилия в упругодемпфирующем элементе (подлежит измерению в процессе управления или определению на основании измеренных параметров, например, текущих прогибов и скоростей прогибов);
Pi - искомое значение усилия в упругодемпфирующем элементе.
Для определения величин ΔPi составим систему уравнений
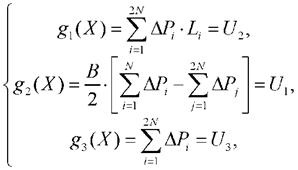
где x = {xi = ΔPi} - вектор искомых переменных;
Li - расстояние от центра масс колесной машины до места крепления
i-ого упругодемпфирующего элемента подвески;
В - рессорная колея колесной машины.
Сформулируем критерий оптимальности, на основании которого будем определять значения искомых переменных. Наиболее целесообразным в данном случае является получение таких значений Pi, чтобы выполнялось условие
∆Pi=Piд - Pi→ 0, i=1, 2, …, 2N,
где Piд - текущие значения усилий в упругодемпфирующих элементах подвески.
Сформулируем квадратичный критерий оптимальности следующим образом:
| (12) |
Полученная задача является задачей оптимизации при наличии ограничений в виде равенств. Необходимые условия минимума функции (12) записываются следующим образом [23]:
| (13) |
Здесь ![]() - неопределенные множители Лагранжа.
- неопределенные множители Лагранжа.
В нашем случае уравнения (13) примут вид
| (14) |
Система (14) является линейной системой, содержащей 2N+3 алгебраических уравнений относительно 2N+3 неизвестных ΔPi, λ1, λ 2, λ 3, из которой легко определяются ΔPi.
5. Результаты моделирования
Разработанный алгоритм управления был апробирован путем моделирования движения многоосного колесного шасси с колесной формулой 8×8 полной массой 60 т в повороте, при торможении, при переезде единичной неровности. Для описания движения колесного шасси по дорожной поверхности была использована математическая модель, разработанная на кафедре «Колесные машины» МГТУ им. Н.Э. Баумана [24]. Особенностью математической модели движения МКМ по неровностям является то, что скорость машины задается не принудительно, а формируется силами взаимодействия вращающихся колесных движителей с опорным основанием. Это позволяет получить высокую точность при моделировании реальных процессов движения МКМ.
5.1. Динамическая стабилизация бокового крена корпуса многоосной колесной машины при движении в повороте
Движение колесной машины в повороте моделировалось при следующих параметрах: скорость движения 20 км/ч; радиус поворота 10 м; дорожная поверхность – ровная недеформируемая; протяженность поворота - поворот на 90 градусов. На рис. 2 приведен переходный процесс бокового крена корпуса колесной машины при движении «вход в поворот – движение в повороте – выход из поворота» для случая неуправляемой подвески, на рис. 3– то же, но для случая управляемой подвески. Из приведенных графиков видно, что амплитуда крена корпуса в случае работы системы управления меньше в 4,7 раза по сравнению с неуправляемой системой подрессоривания.
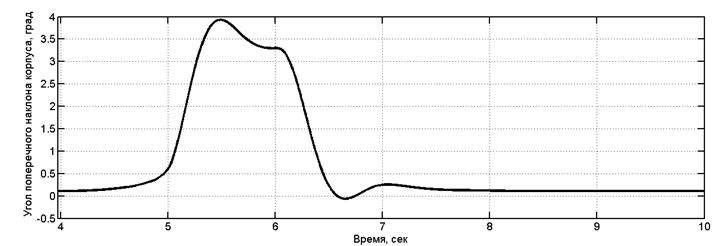
Рис. 2. Переходный процесс бокового крена корпуса МКМ при движении в повороте
(неуправляемая подвеска)
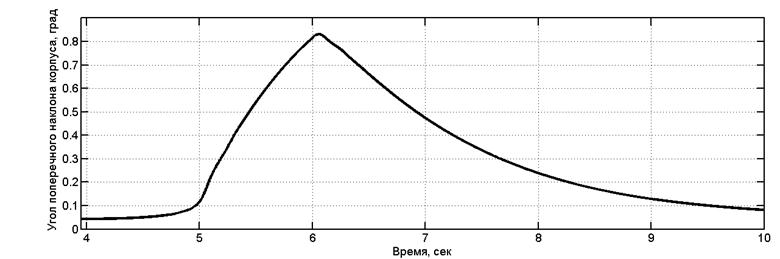
Рис. 3. Переходный процесс бокового крена корпуса МКМ при движении в повороте
(управляемая подвеска)
5.2. Динамическая стабилизация продольного крена корпуса многоосной колесной машины при торможении
Движение машины с колесной формулой 8х8 при торможении моделировалось при следующих параметрах: начальная скорость движения 36 км/ч (10 м/с); дорожная поверхность – ровная недеформируемая. На рис. 4 приведен график изменения скорости при торможении. На рис. 5 приведен переходный процесс продольного наклона корпуса колесной машины при торможении для неуправляемой подвески, на рис. 6 – то же, но для управляемой подвески. Из приведенных графиков видно, что амплитуда крена корпуса в случае управляемой системы подрессоривания меньше в 1,5 раза по сравнению со случаем неуправляемой подвески.
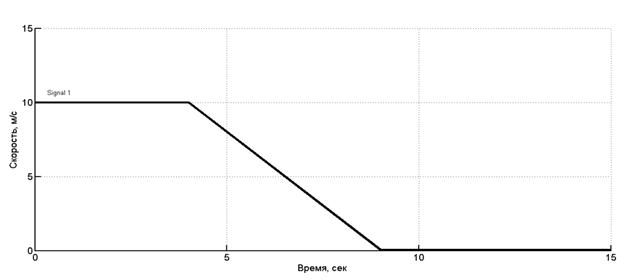
Рис. 4. График изменения скорости при торможении

Рис. 5. Переходный процесс продольного крена корпуса при торможении (неуправляемая подвеска)
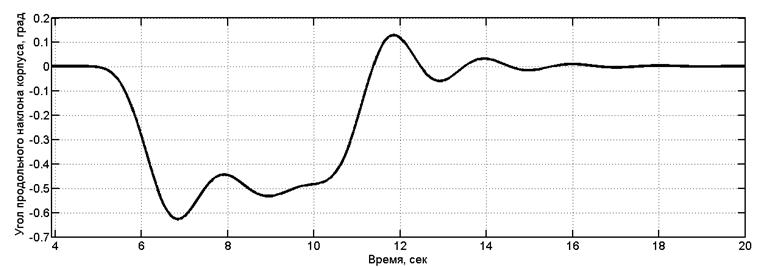
Рис. 6. Переходный процесс продольного крена корпуса при торможении (управляемая подвеска)
5.3. Динамическая стабилизация корпуса многоосной колесной машины при переезде единичной неровности
Движение колесной машины с колесной формулой 8х8 при переезде эскарпа моделировалось при следующих значениях параметров: скорость движения 10 км/ч; дорожная поверхность – ровная недеформируемая; высота эскарпа – 0,15 м. На рис. 7 приведен график изменения продольного угла наклона корпуса для случая неуправляемой подвески, на рис. 8 - то же для управляемой системы подрессоривания.
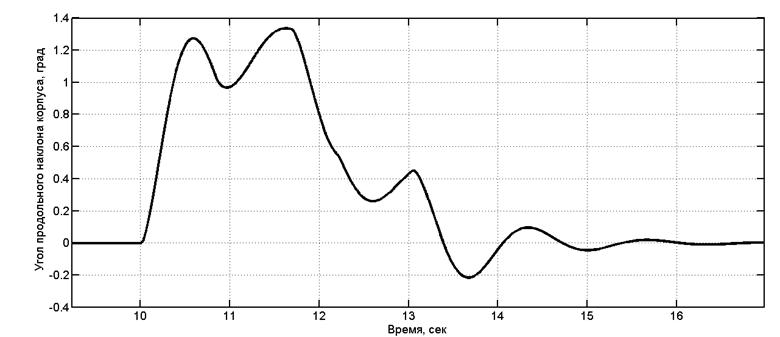
Рис. 7. График изменения продольного угла наклона корпуса для случая неуправляемой подвески (переезд через эскарп)

Рис. 8. График изменения продольного угла наклона корпуса для случая управляемой подвески (переезд через эскарп)
Из приведенных графиков видно, что в случае управляемой подвески максимальное значение угла наклона корпуса уменьшилось на 15 % по сравнению со случаем неуправляемой системы подрессоривания.
Заключение
В работе решены следующие задачи:
· впервые сформулирована задача оптимального управления подвеской МКМ с целью динамической стабилизации корпуса машины;
· предложен математический закон динамической стабилизации корпуса МКМ, обеспечивающий эффективное выравнивание машины при повороте, торможении, переезде единичных неровностей;
· доказана эффективность предложенного закона управления с помощью методов имитационного моделирования движения МКМ в повороте, при торможении, переезде единичной неровности.
Предложенный закон может быть применен в системах управления подвеской МКМ, снабженной как магнитореологическими амортизаторами, так и управляемыми пневмогидравлическими рессорами. Дальнейшее развитие данного направления возможно на пути создания энергоэффективных систем управления подвеской МКМ, обеспечивающих непрерывное управляющее воздействие на корпус машины.
Список литературы
1. Белоусов Б.Н., Попов С.Д. Колесные транспортные средства особо большой грузоподъемности. Конструкция. Теория. Расчет. / Под общ. ред. Б.Н. Белоусова. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. – 728 с.
2. Балагула В.Я., Гайцгори М.М. Выбор структуры управления и параметров активной подвески землеройно-транспортных машин // Труды ВНИИСтройдормаша. - 1977. - Вып. 75. - С. 39-48.
3. Выговский В.В. О синтезе управлений в активной виброзащитной системе твердого тела // Управляемые механические системы. - Иркутск, 1979. - С. 41-51.
4. Елисеев С. В. Теория активных виброзащитных систем и ее приложения: Автореф. дисс. ... докт. техн. наук. - Иркутск, 1973. – 34 с.
5. Динамика управляемых механических систем / Под. ред. С.В. Елисеева.- Иркутск: ИПИ, 1982. – 186 с.
6. Коловский M.3. Об оптимизации активных виброзащитных систем // Машиноведение. - 1977. - N 6. - С. 42-46.
7. Фролов К. В., Фурман Ф.А. Прикладная теория виброзащитных систем. - М.: Машиностроение, 1980. – 276 с.
8. Шарапов В.Д. Активные подвески транспортных средств. - Рига: РВВПКУ, 1980. – 261 с.
9. Фурунжиев P.И., Останин А. Н. Управление колебаниями многоопорных машин. - М.: Машиностроение, 1984. – 206 с.
10. Кольцов В.И. Принципиальные возможности подвески наземных видов транспорта: Дисс. . . . канд. техн. наук. Специальность 05.05.03 - Автомобили и тракторы - M., 1967. – 231 с.
11. Sutton Н.В. Synthesis of active suspension systems: Ph. D. thesis. Salford, 1978. – 86 p.
12. Tompson A. Design of active suspensions // Proc. Inst. Mech. Eng. - 1970-71. V. 185. - P. 553-563.
13. Динамика управляемых механических систем / Под. ред. С.В. Елисеева.- Иркутск, ИПИ, 1982. – 186 с.
14. Андрющенко В.А. Теория систем автоматического управления: Учебное пособие.- Л.; Издательство Ленинградского университета, 1990.- 256 с.
15. Алиев Ф.А., Ларин В.Б., Науменко К.И. и др. Оптимизация линейных инвариантных во времени систем управления.- Киев: Наукова думка, 1978.- 327 с.
16. Иванов В.А., Фалдин Ф.В. Теория оптимальных систем автоматического управления.- М.: Наука, 1981.- 336 с.
17. Летов А.М. Динамика полетов и управление. – М.: Наука, 1969. – 312 с.
18. Деруссо П., Рой Р., Клоуз Ч. Пространство состояний в теории управления. – М.: Наука, 1970. – 484 с.
19. Салуквадзе М.Е. Об оптимизации векторных функционалов // Автоматика и телемеханика. – 1971. - №9. – С. 5 – 15.
20. Аврамов В.П. Александров Е.Е. О выборе показателя качества в теории аналитического конструирования оптимальных регуляторов // Известия ВУЗов. Приборостроение. – 1976. - №10. – С. 32 – 36.
21. Александров Е.Е., Бех М.Е. Автоматизированное проектирование динамических систем с помощью функций Ляпунова. – Харьков: Основа, 1994. – 113 с.
22. Александрова И.Е., Александрова Т.Е. О выборе весовых коэффициентов оптимизируемого функционала в теории аналитического конструирования оптимальных регуляторов // Радіоелектроніка, інформатика, управління. – 2005. - №4. - С. 135 – 137.
23. Банди Б. Методы оптимизации. Вводный курс: Пер. с англ.- М.: Радио и связь, 1988.- 128 с.
24. Проектирование полноприводных колесных машин: Учебник для вузов: В 3 т. Т.3 / Б.А. Афанасьев, Б.Н. Белоусов, Л.Ф. Жеглов и др.; Под ред. А.А. Полунгяна. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2008. – 432 с.
Публикации с ключевыми словами: аналитическое конструирование оптимальных регуляторов, квадратичный функционал качества управления, адаптивная система управления подвеской многоосных колесных машин, динамическая стабилизация
Публикации со словами: аналитическое конструирование оптимальных регуляторов, квадратичный функционал качества управления, адаптивная система управления подвеской многоосных колесных машин, динамическая стабилизация
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||