научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2011
УДК.62-522.2
МГТУ им. Н.Э. Баумана
Введение
Стремление повысить эффективность применения многоосных колесных машин (МКМ) в настоящее время заставляет разработчиков обращать внимание на такой аспект, как увеличение средней скорости движения машин [1].
Как известно, максимальная скорость движения является ограниченной и определяется условиями движения и техническими характеристиками МКМ. Ограничения, главным образом зависящие от дорожных условий, делятся на две группы: ограничения по силе тяги и, так называемые, прямые ограничения [2]. Увеличение удельной мощности современных машин позволили снять ряд ограничений первой группы. Вторая группа объединяет:
- ограничения скорости, определяемые кинематическими характеристиками трансмиссии;
- ограничения по управляемости, связанные со способностью машины вписываться в реальную кривизну трассы;
- ограничения по опасности возникновения неуправляемого движения;
- ограничения вследствие возникновения предельных ускорений корпуса машины при движении по неровностям, которые могут привести к утомляемости и травмам экипажа и выходу из строя установленного оборудования.
В этой связи проблема совершенствования систем подрессоривания МКМ, направленного на повышение скорости движения по неровностям, является актуальной.
Одним из перспективных путей повышения плавности хода МКМ является разработка динамических активных систем подрессоривания, а также законов управления такими системами. Под динамическими системами управления в данной работе понимаются системы, работающие в темпе реального времени с текущими (мгновенными) значениями фазовых координат. Этим динамические системы отличаются от статических, работающих по осредненному по времени сигналу. Активными будем называть системы управления, для работы которых требуется подведение энергии от внешних источников.
Теоретические аспекты активных виброзащитных систем для общего случая подрессоривания твердого тела, а также частных случаев, например для подвески сиденья водителя, исследовали многие ученые: Балагула В.Я., Гайцгори М.М., Генкин М.Д., Яблонский В.В., Елисеев С.А, Иносов С.В., Синев А.В., Фурман Ф.А. и др. [3 – 8]. Применительно к автомобилям активное подрессоривание рассматривали в своих работах Кольцов В.И., Фурунжиев Р.И., Останин А.Н., Шарапов В.Д. [9, 10, 11], зарубежные ученые: Саттон X.Б., Томпсон А.Г. и др. [12, 13]. Исследователями отмечается, что наиболее эффективны с точки зрения плавности хода активные подвески.
Однако внедрение систем активного управления подвеской МКМ сдерживается отсутствием законов непрерывного управления упруго-демпфирующими элементами системы подрессоривания [1].
Целью работы является разработка законов оптимального управления подвеской МКМ, обеспечивающих снижение вибронагруженности водителя при кинематическом воздействии
1. Синтез динамической непрерывной системы управления, обеспечивающей гашение колебаний корпуса многоосной колесной машины
Будем считать корпус абсолютно твердым телом, подвеска колес выполнена по "свечной" схеме [1]. Рассмотрим линеаризованную модель движения корпуса МКМ относительно только трех фазовых координат (рис. 1):
- относительно вертикальной оси Z связанной с корпусом МКМ системы координат;
- вращение корпуса относительно главной оси инерции Х связанной с корпусом системы координат;
- вращение корпуса относительно главной оси инерции Y связанной с корпусом системы координат;
- вращение корпуса относительно главной оси инерции Y связанной с корпусом системы координат.
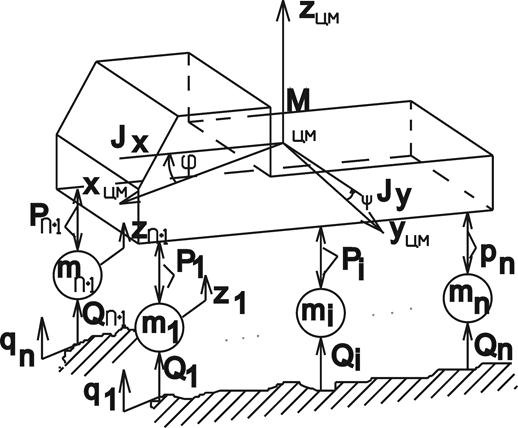
Рис. 1. Расчетная схема многоопорной колебательной системы МКМ
В результате получим следующие упрощенные уравнения движения корпуса многоосной машины
| (1) |
где
U1 - управляющий момент, создаваемый упругодемпфирующими элементами подвески относительно оси Х (приложен к центру масс корпуса многоосного шасси);
U2- управляющий момент, создаваемый упругодемпфирующими элементами подвески относительно оси Y (приложен к центру масс корпуса многоосного шасси);
U3 - управляющий главный вектор сил, создаваемый упругодемпфирующими элементами подвески в вертикальном направлении (приложен к центру масс корпуса многоосного шасси);
ωx – угловая скорость корпуса относительно оси х;
ωy – угловая скорость корпуса относительно оси y;
Vz – скорость корпуса относительно оси z;
φ – угол наклона корпуса относительно оси х;
ψ– угол наклона корпуса относительно оси y;
z – перемещение центра масс относительно оси z;
Jx, Jy – моменты инерции подрессоренной массы МКМ относительно осей x и y соответственно;
Мподр – подрессоренная масса.
В данном случае управление U1 и U2 являются управляющими моментами относительно, соответственно, продольной оси автомобиля Х и поперечной оси Y, проходящей через его центр тяжести. Управление U3 представляет собой управляющий вектор сил, параллельных вертикальной оси Z. Все управляющие воздействия создаются управляемыми упруго-демпфирующими элементами подвески многоосной колесной машины.
Система (1) может быть разбита на три независимых канала управления: два канала, обеспечивающих гашение угловых колебаний корпуса и его стабилизацию по углу наклона, и один канал - по гашению его вертикальных колебаний.
При синтезе оптимальных систем широко применяют квадратичные интегральные критерии качества, содержащие координаты объекта и управления [14, 15].
Исходная система уравнений состояния (1) представляет собой линейную систему, описываемую векторным дифференциальным уравнением
 (2)
(2)
где X(t) - n-мерный вектор состояния;
A(t), B(t)- матричные функции времени соответственно порядков n×n; n×m;
u(t) - m-мерный вектор управления.
Вектор управления U(t) = [u1(t), …, um(t)]T по понятным физическим причинам является ограниченным, т.е. принадлежащим замкнутому множеству
![]()
Для выбора критерия качества управления сформулируем предъявляемые к нему требования.
Наиболее универсальным является критерий качества, основанный на введении оптимизируемого функционала интегрального типа. Использование интегральных критериев, в частности, квадратичных функционалов, позволяет определить требования к переходным процессам системы управления заданием значений небольшого числа их весовых коэффициентов, практически произвольный выбор которых обеспечивает фундаментальное свойство синтезируемой системы − ее асимптотическую устойчивость [15]. Итерационный целенаправленный перебор весовых коэффициентов, как правило, удовлетворяет разумные требования к первичным показателям качества переходных процессов. Главное достоинство данного способа формализации заключается в том, что он позволяет использовать для синтеза системы управления сложными объектами результаты теории оптимального управления и теории аналитического конструирования оптимальных регуляторов (АКОР) [16]. Все более широкое применение в прикладных задачах управления сложными производственными объектами методов АКОР связано с такими их достоинствами, как общность, предельная формализация, логическая завершенность, принципиальная математическая простота.
Таким образом, для объектов управления (2) приходим к необходимости решения задачи АКОР по соответствующему интегральному критерию. При выборе функционала качества управления (при постановке задачи АКОР) предполагается, что для систем подрессоривания многоосных колесных машин, функционирующих в условиях действия возмущений значительной амплитуды (мощности), желательна стабилизация выходных переменных (скорости, ускорения и перемещения подрессоренных масс) на определенном уровне для улучшения показателей вибронагруженности и устойчивости.
В настоящее время в теории и практике оптимального управления широкое распространение получили интегральные квадратичные обобщенные функционалы качества систем автоматического управления вида [16] вида
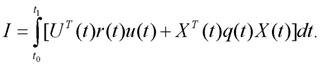 (3)
(3)
ЗдесьU(t) - m-мерный вектор управления; X(t) - n-мерный вектор состояния; r(t)>0, q(t)>0 – весовые коэффициенты.
Значение функционала I зависит от начального состояния Х(t0), момента времени t0 и управления u(t) в течение интервала (t0,t1). Задача оптимального регулирования - минимизировать функционал (3).
2. Разработка закона оптимального управления гашением угловых и вертикальных колебаний корпуса многоосной колесной машины
2.1. Гашение угловых колебания корпуса МКМ
Пусть х1 = φ - угол наклона корпуса; х2 = ω - угловая скорость. Из уравнений (1) может быть получена система уравнений, описывающих угловые колебания корпуса МКМ, в виде
| (4) |
Здесь J=Jxили J=Jy.
В данном случае управление U являются управляющим моментом относительно соответствующей оси автомобиля, проходящей через его центр тяжести. Все управляющие воздействия создаются управляемыми упругодемпфирующими элементами подвески машины.
Требуется найти управление, которое доставляет минимум функционалу
 (5)
(5)
где r > 0; qi> 0; x - вектор состояния объекта; U - вектор управления объекта.
Потребуем, чтобы удовлетворялись граничные условия
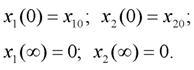 (6)
(6)
Таким образом, будем решать задачу со свободным правым концом, поскольку при динамическом управлении подвеской нет смысла накладывать какие-либо ограничения на значения фазовых координат, ибо мы не сможем добиться нулевых значений, а можем только лишь уменьшить их значения. На этом этапе синтеза оптимального регулятора ограничений на фазовые координаты и управляющие воздействия не накладывается.
Сформулированная выше задача представляет собой задачу Лагранжа на условный экстремум [16]. В соответствии с методом решения задачи Лагранжа составим вспомогательный функционал
 (7)
(7)
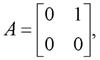

Запишем для функционала (7) уравнения Эйлера-Лагранжа
 (8)
(8)
где Ф(xi, Ui) - подинтегральная функция функционала (7). К уравнениям (8) необходимо добавить уравнения связей (4). Получим следующую систему сопряженных уравнений
 (9)
(9)
Запишем характеристическое уравнение для линейной однородной системы дифференциальных уравнений (9)
![]()
 (10)
(10)
или

Поскольку r> 0, корни характеристического уравнения будут равны
 (11)
(11)
Согласно граничным условиям (6) отбросим собственные числа, лежащие в правой полуплоскости, что приводит к синтезу устойчивой системы автоматического управления. Далее известными методами [16] определяем общее решение системы (9)
![]() (12)
(12)
![]() (13)
(13)
где ![]() - корни характеристического уравнения (10), которые расположены в левой полуплоскости; С1, С2 - константы.
- корни характеристического уравнения (10), которые расположены в левой полуплоскости; С1, С2 - константы.
Разрешим равенства (12) и (13) относительно ![]() и
и![]() . Получим следующие выражения:
. Получим следующие выражения:


Тогда из второго уравнения системы (4) найдем выражение для закона оптимального управления гашением угловых колебаний
 (14)
(14)
Система (4) с управлением (14) будет устойчивой, поскольку корни ее характеристического уравнения ![]() расположены в левой полуплоскости. Разработанный закон оптимального управления может быть использован для управления отдельно для каждого из углов наклона корпуса.
расположены в левой полуплоскости. Разработанный закон оптимального управления может быть использован для управления отдельно для каждого из углов наклона корпуса.
2.2. Гашение вертикальных колебания корпуса МКМ
Перейдем к построению закона управления, обеспечивающей гашение вертикальных колебаний корпуса. Исходное дифференциальное уравнение имеет вид
 (15)
(15)
Введем новые обозначения. Пусть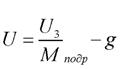 . Тогда уравнение (15) можно записать в виде
. Тогда уравнение (15) можно записать в виде
 (16)
(16)
Пусть х1 = z – вертикальное перемещение центра масс корпуса;
х2 = Vz – вертикальная скорость центра масс корпуса. Тогда систему (16) можно переписать в виде
 (17)
(17)
Управление U3 являются управляющим главным вектором сил, проходящим через центр масс транспортного средства. Требуется найти управление, которое доставляет минимум функционалу
 (18)
(18)
где r > 0; qi> 0; x - вектор состояния объекта; U - вектор управления объекта.
Потребуем, чтобы удовлетворялись граничные условия
 (19)
(19)
Сформулированная задача представляет собой задачу Лагранжа на условный экстремум [16]. В соответствии с методом решения задачи Лагранжа составим вспомогательный функционал
 (20)
(20)
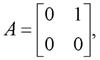
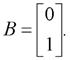
Для функционала (20) уравнения Эйлера-Лагранжа имеют вид (8). К уравнениям (8) необходимо добавить уравнения связей (17). Таким образом, получим систему сопряженных уравнений
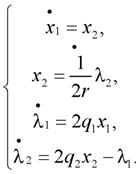 (21)
(21)
Запишем характеристическое уравнение для линейной однородной системы дифференциальных уравнений (21)
![]()
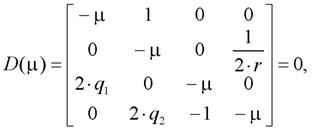 (22)
(22)
или

Поскольку r> 0, корни характеристического уравнения будут равны
 (23)
(23)
Согласно граничным условиям (19) отбросим собственные числа, лежащие в правой полуплоскости, что, как указывалось ранее, приводит к синтезу устойчивой системы автоматического управления. Далее известными методами [16] определяется общее решение системы (21), которое может быть записано в виде
![]() (24)
(24)
![]() (25)
(25)
где ![]() - корни характеристического уравнения (22), которые расположены в левой полуплоскости. Разрешим равенства (24) и (25) относительно
- корни характеристического уравнения (22), которые расположены в левой полуплоскости. Разрешим равенства (24) и (25) относительно ![]() и
и![]() . Получим выражения
. Получим выражения


Из второго уравнения системы (17) найдем закон для оптимального управления гашением вертикальных колебаний
 (26)
(26)
Система (17) с управлением (26) будет устойчивой, поскольку корни ее характеристического уравнения ![]() расположены в левой полуплоскости. Окончательно искомое выражение для закона оптимального управления имеет вид
расположены в левой полуплоскости. Окончательно искомое выражение для закона оптимального управления имеет вид
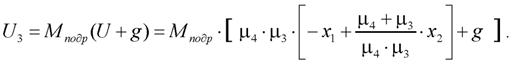 (27)
(27)
3. Результаты моделирования
Разработанные законы оптимального управления были апробированы путем моделирования прямолинейного равномерного движения многоосного колесного шасси с колесной формулой 8×8 полной массой 60 т на грунтовой дороге с различными скоростями движения. Для описания движения колесного шасси по дорожной поверхности была использована математическая модель, разработанная на кафедре «Колесные машины» МГТУ им. Н.Э. Баумана [17]. Особенностью математической модели движения МКМ по неровностям является то, что скорость машины задается не принудительно, а формируется силами взаимодействия вращающихся колесных движителей с опорным основанием. Это позволяет получить высокую точность при моделировании реальных процессов движения МКМ.
На рис. 2 – 4 приведены уровни виброускорений на месте водителя в октавных полосах частот для случаев управляемой и неуправляемой подвески при движении по грунтовой дороге в диапазоне скоростей 10 … 70 км/ч.

Рис. 2. Уровни виброускорений на месте водителя (I октава)

Рис. 3. Уровни виброускорений на месте водителя (II октава)

Рис. 4. Уровни виброускорений на месте водителя (III октава)
Анализ графиков (рис. 2 – 4) позволяет сделать следующие выводы.
1) Разработанные законы оптимального управления гашением колебаний корпуса МКМ позволяют эффективно подавлять виброускорения подрессоренной массы во всем рабочем диапазоне частот (0…5 Гц).
2) В случае движения с управляемой подвеской по грунтовой дороге уровни виброускорений по октавам на месте водителя снижаются на 2 … 6 дБ в зависимости от скорости движения.
3) Результаты моделирования показывают, что при движении по грунтовой дороге с управляемой по предложенным законам подвеской допустимые скорости движения могут быть повышены с 20 км/час до 70 км/час по критерию плавности хода (согласно нормам ГОСТ 12.1.012-2004).
Заключение
В работе решены следующие задачи:
· предложены законы оптимального управления гашением колебаний корпуса МКМ, обеспечивающие снижение вибронагруженности водителя и увеличение допустимых скоростей движения, отличающиеся возможностью формирования управляющих воздействий в темпе реального времени;
· доказана эффективность предложенных законов управления с помощью методов имитационного моделирования движения МКМ по грунтовой дороге при кинематическом воздействии.
Предложенные законы оптимального управления могут быть применены в системах управления подвеской МКМ, снабженной как магнитореологическими амортизаторами, так и управляемыми пневмогидравлическими рессорами. Дальнейшее развитие данного направления возможно на пути создания энергоэффективных систем управления подвеской МКМ, обеспечивающих непрерывное управляющее воздействие на корпус машины.
Список литературы
1. Белоусов Б.Н., Попов С.Д. Колесные транспортные средства особо большой грузоподъемности. Конструкция. Теория. Расчет. / Под общ. ред. Б.Н. Белоусова. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. – 728 с.
2. Сухоруков А.В. Управлениe демпфирующими элементами в системе подрессоривания быстроходной гусеничной машины. - Дисс. ... канд. техн. наук. Специальность 05.05.03 - Автомобили и тракторы.- М.: 2003.- 204 с.
3. Балагула В.Я., Гайцгори М.М. Выбор структуры управления и параметров активной подвески землеройно-транспортных машин
// Труды ВНИИСтройдормаша. - 1977. - Вып. 75. - С. 39-48.
4. Выговский В.В. О синтезе управлений в активной вибр3ващитной системе твердого тела // Управляемые механические системы. - Иркутск, 1979. - С. 41-51.
5. Елисеев С.В. Теория активных виброзащитных систем и ее приложения: Автореф. дисс. ... докт. техн. наук. - Иркутск, 1973. – 34 с.
6. Динамика управляемых механических систем / Под. ред. С.В. Елисеева.- Иркутск: ИПИ, 1982. – 186 с.
7. Коловский M.3. Об оптимизации активных виброзащитных систем
// Машиноведение. - 1977. - N 6. - С. 42-46.
8. Фролов К.В., Фурман Ф.А. Прикладная теория виброзащитных систем. - М.: Машиностроение, 1980. - 276 с.
9. Шарапов В.Д. Активные подвески транспортных средств. - Рига: РВВПКУ, 1980. - 261 с.
10. Фурунжиев P.И., Останин А. Н. Управление колебаниями многоопорных машин. - М.: Машиностроение, 1984. – 206 с.
11. Кольцов В.И. Принципиальные возможности подвески наземных видов транспорта: Дисс. . . . канд. техн. наук. Специальность 05.05.03 - Автомобили и тракторы - M., 1967. - 231 с.
12. Sutton Н.В. Synthesis of active suspension systems: Ph. D. thesis. Salford, 1978. – 86 p.
13. Tompson A. Design of active suspensions // Proc. Inst. Mech. Eng. - 1970-71. V. 185. - P. 553-563.
14. Андрющенко В.А. Теория систем автоматического управления: Учебное пособие.- Л.; Издательство Ленинградского университета, 1990.- 256 с.
15. Алиев Ф.А., Ларин В.Б., Науменко К.И. и др. Оптимизация линейных инвариантных во времени систем управления.- Киев: Наукова думка, 1978.- 327 с.
16. Иванов В.А., Фалдин Ф.В. Теория оптимальных систем автоматического управления.- М.: Наука, 1981.- 336 с.
17. Проектирование полноприводных колесных машин: Учебник для вузов: В 3 т. Т.3 / Б.А. Афанасьев, Б.Н. Белоусов, Л.Ф. Жеглов и др.; Под ред. А.А. Полунгяна. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2008. – 432 с.
Публикации с ключевыми словами: плавность хода, аналитическое конструирование оптимальных регуляторов, квадратичный функционал качества управления, адаптивная система управления подвеской многоосных колесных машин
Публикации со словами: плавность хода, аналитическое конструирование оптимальных регуляторов, квадратичный функционал качества управления, адаптивная система управления подвеской многоосных колесных машин
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||





